Free Lesson Library

These incredibly powerful, flexible activities can be used with a variety of content and contexts.
These games are chosen for their simplicity and depth.
Problems that resist easy solutions while encouraging perseverance and deeper understanding.
- All Lessons
Selecting this shows all the free lessons in our library.
Every student deserves to have the opportunity to problem-solve and engage in genuine mathematical thinking. Rich tasks are designed to make these rich learning experiences possible. We’ve written these tasks to launch quickly, engage students, and promote the habits of mind mathematicians need: perseverance & pattern-seeking, courage & curiosity, organization & communication.
This free video PD series will help you get the most out of the tasks below.

Lessons - Rich Tasks
- Common Core Math Practices
- Counting and Cardinality
- Expressions and Equations
- Measurement and Data
- Number System
- Numbers and Operations in Base Ten
- Numbers and Operations in Fraction
- Operations and Algebraic Thinking
- Ratio and Proportion
- Exploration
- Divisibility
- Measurement
- Mental Math Games
- Multiplication
- Place Value
- Subtraction

Join Our Mailing List
Get tons of free content, like our Games to Play at Home packet, puzzles, lessons, and more!

Problem Solving Activities: 7 Strategies
- Critical Thinking

Problem solving can be a daunting aspect of effective mathematics teaching, but it does not have to be! In this post, I share seven strategic ways to integrate problem solving into your everyday math program.
In the middle of our problem solving lesson, my district math coordinator stopped by for a surprise walkthrough.
I was so excited!
We were in the middle of what I thought was the most brilliant math lesson– teaching my students how to solve problem solving tasks using specific problem solving strategies.
It was a proud moment for me!
Each week, I presented a new problem solving strategy and the students completed problems that emphasized the strategy.
Genius right?
After observing my class, my district coordinator pulled me aside to chat. I was excited to talk to her about my brilliant plan, but she told me I should provide the tasks and let my students come up with ways to solve the problems. Then, as students shared their work, I could revoice the student’s strategies and give them an official name.
What a crushing blow! Just when I thought I did something special, I find out I did it all wrong.
I took some time to consider her advice. Once I acknowledged she was right, I was able to make BIG changes to the way I taught problem solving in the classroom.
When I Finally Saw the Light
To give my students an opportunity to engage in more authentic problem solving which would lead them to use a larger variety of problem solving strategies, I decided to vary the activities and the way I approached problem solving with my students.
Problem Solving Activities
Here are seven ways to strategically reinforce problem solving skills in your classroom.

Seasonal Problem Solving
Many teachers use word problems as problem solving tasks. Instead, try engaging your students with non-routine tasks that look like word problems but require more than the use of addition, subtraction, multiplication, and division to complete. Seasonal problem solving tasks and daily challenges are a perfect way to celebrate the season and have a little fun too!
Cooperative Problem Solving Tasks
Go cooperative! If you’ve got a few extra minutes, have students work on problem solving tasks in small groups. After working through the task, students create a poster to help explain their solution process and then post their poster around the classroom. Students then complete a gallery walk of the posters in the classroom and provide feedback via sticky notes or during a math talk session.
Notice and Wonder
Before beginning a problem solving task, such as a seasonal problem solving task, conduct a Notice and Wonder session. To do this, ask students what they notice about the problem. Then, ask them what they wonder about the problem. This will give students an opportunity to highlight the unique characteristics and conditions of the problem as they try to make sense of it.
Want a better experience? Remove the stimulus, or question, and allow students to wonder about the problem. Try it! You’ll gain some great insight into how your students think about a problem.

Math Starters
Start your math block with a math starter, critical thinking activities designed to get your students thinking about math and provide opportunities to “sneak” in grade-level content and skills in a fun and engaging way. These tasks are quick, designed to take no more than five minutes, and provide a great way to turn-on your students’ brains. Read more about math starters here !
Create your own puzzle box! The puzzle box is a set of puzzles and math challenges I use as fast finisher tasks for my students when they finish an assignment or need an extra challenge. The box can be a file box, file crate, or even a wall chart. It includes a variety of activities so all students can find a challenge that suits their interests and ability level.
Calculators
Use calculators! For some reason, this tool is not one many students get to use frequently; however, it’s important students have a chance to practice using it in the classroom. After all, almost everyone has access to a calculator on their cell phones. There are also some standardized tests that allow students to use them, so it’s important for us to practice using calculators in the classroom. Plus, calculators can be fun learning tools all by themselves!
Three-Act Math Tasks
Use a three-act math task to engage students with a content-focused, real-world problem! These math tasks were created with math modeling in mind– students are presented with a scenario and then given clues and hints to help them solve the problem. There are several sites where you can find these awesome math tasks, including Dan Meyer’s Three-Act Math Tasks and Graham Fletcher’s 3-Acts Lessons .
Getting the Most from Each of the Problem Solving Activities
When students participate in problem solving activities, it is important to ask guiding, not leading, questions. This provides students with the support necessary to move forward in their thinking and it provides teachers with a more in-depth understanding of student thinking. Selecting an initial question and then analyzing a student’s response tells teachers where to go next.
Ready to jump in? Grab a free set of problem solving challenges like the ones pictured using the form below.
Which of the problem solving activities will you try first? Respond in the comments below.

Shametria Routt Banks

- Assessment Tools
- Content and Standards
- Differentiation
- Math & Literature
- Math & Technology
- Math Routines
- Math Stations
- Virtual Learning
- Writing in Math
You may also like...

2 Responses
This is a very cool site. I hope it takes off and is well received by teachers. I work in mathematical problem solving and help prepare pre-service teachers in mathematics.
Thank you, Scott! Best wishes to you and your pre-service teachers this year!
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
This site uses Akismet to reduce spam. Learn how your comment data is processed .
©2024 The Routty Math Teacher. All Rights Reserved. Designed by Ashley Hughes.
Privacy overview, grade level.

Become a Problem-solving School
Or search by topic
Number and algebra.
- Place value and the number system
- Fractions, decimals, percentages, ratio and proportion
- Calculations and numerical methods
- Algebraic expressions, equations and formulae
- Coordinates, functions and graphs
- Patterns, sequences and structure
- Properties of numbers
Geometry and measure
- 3D geometry, shape and space
- Transformations and constructions
- Vectors and matrices
- Measuring and calculating with units
- Pythagoras and trigonometry
- Angles, polygons, and geometrical proof
Probability and statistics
- Handling, processing and representing data
- Probability
Working mathematically
- Thinking mathematically
- Mathematical mindsets
Advanced mathematics
- Decision mathematics and combinatorics
- Advanced probability and statistics
For younger learners
- Early years foundation stage
A Guide to Problem Solving
When confronted with a problem, in which the solution is not clear, you need to be a skilled problem-solver to know how to proceed. When you look at STEP problems for the first time, it may seem like this problem-solving skill is out of your reach, but like any skill, you can improve your problem-solving with practice. How do I become a better problem-solver? First and foremost, the best way to become better at problem-solving is to try solving lots of problems! If you are preparing for STEP, it makes sense that some of these problems should be STEP questions, but to start off with it's worth spending time looking at problems from other sources. This collection of NRICH problems is designed for younger students, but it's very worthwhile having a go at a few to practise the problem-solving technique in a context where the mathematics should be straightforward to you. Then as you become a more confident problem-solver you can try more past STEP questions. One student who worked with NRICH said: "From personal experience, I was disastrous at STEP to start with. Yet as I persisted with it for a long time it eventually started to click - 'it' referring to being able to solve problems much more easily. This happens because your brain starts to recognise that problems fall into various categories and you subconsciously remember successes and pitfalls of previous 'similar' problems." A Problem-solving Heuristic for STEP Below you will find some questions you can ask yourself while you are solving a problem. The questions are divided into four phases, based loosely on those found in George Pólya's 1945 book "How to Solve It". Understanding the problem
- What area of mathematics is this?
- What exactly am I being asked to do?
- What do I know?
- What do I need to find out?
- What am I uncertain about?
- Can I put the problem into my own words?
Devising a plan
- Work out the first few steps before leaping in!
- Have I seen something like it before?
- Is there a diagram I could draw to help?
- Is there another way of representing?
- Would it be useful to try some suitable numbers first?
- Is there some notation that will help?
Carrying out the plan STUCK!
- Try special cases or a simpler problem
- Work backwards
- Guess and check
- Be systematic
- Work towards subgoals
- Imagine your way through the problem
- Has the plan failed? Know when it's time to abandon the plan and move on.
Looking back
- Have I answered the question?
- Sanity check for sense and consistency
- Check the problem has been fully solved
- Read through the solution and check the flow of the logic.
Throughout the problem solving process it's important to keep an eye on how you're feeling and making sure you're in control:
- Am I getting stressed?
- Is my plan working?
- Am I spending too long on this?
- Could I move on to something else and come back to this later?
- Am I focussing on the problem?
- Is my work becoming chaotic, do I need to slow down, go back and tidy up?
- Do I need to STOP, PEN DOWN, THINK?
Finally, don't forget that STEP questions are designed to take at least 30-45 minutes to solve, and to start with they will take you longer than that. As a last resort, read the solution, but not until you have spent a long time just thinking about the problem, making notes, trying things out and looking at resources that can help you. If you do end up reading the solution, then come back to the same problem a few days or weeks later to have another go at it.
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry
Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents
As a nonprofit, we need your support to provide a free, world-class education to anyone, anywhere.
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving
Katie Keeton
Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.
Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.
This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.
What are problem-solving strategies?
Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:
- Draw a model
- Use different approaches
- Check the inverse to make sure the answer is correct
Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.
Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques
Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.
20 Math Strategies For Problem-Solving
Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.
Here are 20 strategies to help students develop their problem-solving skills.
Strategies to understand the problem
Strategies that help students understand the problem before solving it helps ensure they understand:
- The context
- What the key information is
- How to form a plan to solve it
Following these steps leads students to the correct solution and makes the math word problem easier .
Here are five strategies to help students understand the content of the problem and identify key information.
1. Read the problem aloud
Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.
2. Highlight keywords
When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.
3. Summarize the information
Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.
4. Determine the unknown
A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.
5. Make a plan
Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.
Strategies for solving the problem
1. draw a model or diagram.
Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out
This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:
| The problem | How to act out the problem |
| Gia has 6 apples. Jordan has 3 apples. How many apples do they have altogether? | Two students use counters to represent the apples. One student has 6 counters and the other student takes 3. Then, they can combine their “apples” and count the total. |
| Michael has 7 pencils. He gives 2 pencils to Sarah. How many pencils does Michael have now? | One student (“Michael”) holds 7 pencils, the other (“Sarah”) holds 2 pencils. The student playing Michael gives 2 pencils to the student playing Sarah. Then the students count how many pencils Michael is left holding. |
3. Work backwards
Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.
For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.
4. Write a number sentence
When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.
5. Use a formula
Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.
Strategies for checking the solution
Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.
There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.
Here are five strategies to help students check their solutions.
1. Use the Inverse Operation
For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.
2. Estimate to check for reasonableness
Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.
3. Plug-In Method
This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓
4. Peer Review
Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.
5. Use a Calculator
A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.
Step-by-step problem-solving processes for your classroom
In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.
Polya’s 4 steps include:
- Understand the problem
- Devise a plan
- Carry out the plan
Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.
Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.
Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving
Resources .
Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.
Explore the range of problem solving resources for 2nd to 8th grade students.
One-on-one tutoring
Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.
Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.
Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.
Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.
READ MORE :
- 8 Common Core math examples
- Tier 3 Interventions: A School Leaders Guide
- Tier 2 Interventions: A School Leaders Guide
- Tier 1 Interventions: A School Leaders Guide
There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model • act it out • work backwards • write a number sentence • use a formula
Here are 10 strategies for problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model • Act it out • Work backwards • Write a number sentence • Use a formula
1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back
Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.
Related articles

5 Tried And Tested Strategies To Increase Student Engagement

Rote Memorization: Is It Effective In Education?

5 Effective Instructional Strategies Educators Can Use In Every Classroom
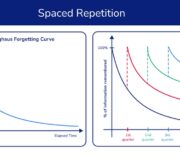
A Teacher’s Guide To Spaced Repetition And Creating An Effective Spaced Repetition Schedule
Ultimate Guide to Metacognition [FREE]
Looking for a summary on metacognition in relation to math teaching and learning?
Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.
Privacy Overview

IMAGES
VIDEO
COMMENTS
Using NRICH Tasks to Develop Key Problem-solving Skills. This article, written for primary teachers, discusses what we mean by 'problem-solving skills' and draws attention to NRICH tasks which can help develop specific skills.
Rich Tasks. Every student deserves to have the opportunity to problem-solve and engage in genuine mathematical thinking. Rich tasks are designed to make these rich learning experiences possible. We’ve written these tasks to launch quickly, engage students, and promote the habits of mind mathematicians need: perseverance & pattern-seeking ...
Use a three-act math task to engage students with a content-focused, real-world problem! These math tasks were created with math modeling in mind– students are presented with a scenario and then given clues and hints to help them solve the problem.
Below you will find some questions you can ask yourself while you are solving a problem. The questions are divided into four phases, based loosely on those found in George Pólya's 1945 book "How to Solve It".
Looking for free math worksheets? You’ve found something even better! That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun! Just choose your grade level or topic to get access to 100% free practice questions ...
Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.