lean six sigma hypothesis statement

Guide: Hypothesis Testing

Author: Daniel Croft

Daniel Croft is an experienced continuous improvement manager with a Lean Six Sigma Black Belt and a Bachelor's degree in Business Management. With more than ten years of experience applying his skills across various industries, Daniel specializes in optimizing processes and improving efficiency. His approach combines practical experience with a deep understanding of business fundamentals to drive meaningful change.

In the world of data-driven decision-making, Hypothesis Testing stands as a cornerstone methodology. It serves as the statistical backbone for a multitude of sectors, from manufacturing and logistics to healthcare and finance. But what exactly is Hypothesis Testing, and why is it so indispensable? Simply put, it’s a technique that allows you to validate or invalidate claims about a population based on sample data. Whether you’re looking to streamline a manufacturing process, optimize logistics, or improve customer satisfaction, Hypothesis Testing offers a structured approach to reach conclusive, data-supported decisions.

The graphical example above provides a simplified snapshot of a hypothesis test. The bell curve represents a normal distribution, the green area is where you’d accept the null hypothesis ( H 0​), and the red area is the “rejection zone,” where you’d favor the alternative hypothesis ( Ha ​). The vertical blue line represents the threshold value or “critical value,” beyond which you’d reject H 0​.

Here’s a graphical example of a hypothesis test, which you can include in the introduction section of your guide. In this graph:

• The curve represents a standard normal distribution, often encountered in hypothesis tests.
• The green-shaded area signifies the “Acceptance Region,” where you would fail to reject the null hypothesis ( H 0​).
• The red-shaded areas are the “Rejection Regions,” where you would reject H 0​ in favor of the alternative hypothesis ( Ha ​).
• The blue dashed lines indicate the “Critical Values” (±1.96), which are the thresholds for rejecting H 0​.

This graphical representation serves as a conceptual foundation for understanding the mechanics of hypothesis testing. It visually illustrates what it means to accept or reject a hypothesis based on a predefined level of significance.

Want exclusive templates, tools and guides?

Join our email list below and for the next 28 days, we will send you exclusive tools, templates and guides unavailable on the website. We developed a short and simple 28-day program designed to develop your ability to implement Lean and Six Sigma methods daily.

What is Hypothesis Testing?

Hypothesis testing is a structured procedure in statistics used for drawing conclusions about a larger population based on a subset of that population, known as a sample. The method is widely used across different industries and sectors for a variety of purposes. Below, we’ll dissect the key components of hypothesis testing to provide a more in-depth understanding.

The Hypotheses: H 0 and Ha

In every hypothesis test, there are two competing statements:

• Null Hypothesis ( H 0) : This is the “status quo” hypothesis that you are trying to test against. It is a statement that asserts that there is no effect or difference. For example, in a manufacturing setting, the null hypothesis might state that a new production process does not improve the average output quality.
• Alternative Hypothesis ( Ha or H 1) : This is what you aim to prove by conducting the hypothesis test. It is the statement that there is an effect or difference. Using the same manufacturing example, the alternative hypothesis might state that the new process does improve the average output quality.

Significance Level ( α )

Before conducting the test, you decide on a “Significance Level” ( α ), typically set at 0.05 or 5%. This level represents the probability of rejecting the null hypothesis when it is actually true. Lower α values make the test more stringent, reducing the chances of a ‘false positive’.

Data Collection

You then proceed to gather data, which is usually a sample from a larger population. The quality of your test heavily relies on how well this sample represents the population. The data can be collected through various means such as surveys, observations, or experiments.

Statistical Test

Depending on the nature of the data and what you’re trying to prove, different statistical tests can be applied (e.g., t-test, chi-square test , ANOVA , etc.). These tests will compute a test statistic (e.g., t , 2 χ 2, F , etc.) based on your sample data.

Here are graphical examples of the distributions commonly used in three different types of statistical tests: t-test, Chi-square test, and ANOVA (Analysis of Variance), displayed side by side for comparison.

• Graph 1 (Leftmost): This graph represents a t-distribution, often used in t-tests. The t-distribution is similar to the normal distribution but tends to have heavier tails. It is commonly used when the sample size is small or the population variance is unknown.

Chi-square Test

• Graph 2 (Middle): The Chi-square distribution is used in Chi-square tests, often for testing independence or goodness-of-fit. Unlike the t-distribution, the Chi-square distribution is not symmetrical and only takes on positive values.

ANOVA (F-distribution)

• Graph 3 (Rightmost): The F-distribution is used in Analysis of Variance (ANOVA), a statistical test used to analyze the differences between group means. Like the Chi-square distribution, the F-distribution is also not symmetrical and takes only positive values.

These visual representations provide an intuitive understanding of the different statistical tests and their underlying distributions. Knowing which test to use and when is crucial for conducting accurate and meaningful hypothesis tests.

Decision Making

The test statistic is then compared to a critical value determined by the significance level ( α ) and the sample size. This comparison will give you a p-value. If the p-value is less than α , you reject the null hypothesis in favor of the alternative hypothesis. Otherwise, you fail to reject the null hypothesis.

Interpretation

Finally, you interpret the results in the context of what you were investigating. Rejecting the null hypothesis might mean implementing a new process or strategy, while failing to reject it might lead to a continuation of current practices.

To sum it up, hypothesis testing is not just a set of formulas but a methodical approach to problem-solving and decision-making based on data. It’s a crucial tool for anyone interested in deriving meaningful insights from data to make informed decisions.

Why is Hypothesis Testing Important?

Hypothesis testing is a cornerstone of statistical and empirical research, serving multiple functions in various fields. Let’s delve into each of the key areas where hypothesis testing holds significant importance:

Data-Driven Decisions

In today’s complex business environment, making decisions based on gut feeling or intuition is not enough; you need data to back up your choices. Hypothesis testing serves as a rigorous methodology for making decisions based on data. By setting up a null hypothesis and an alternative hypothesis, you can use statistical methods to determine which is more likely to be true given a data sample. This structured approach eliminates guesswork and adds empirical weight to your decisions, thereby increasing their credibility and effectiveness.

Risk Management

Hypothesis testing allows you to assign a ‘p-value’ to your findings, which is essentially the probability of observing the given sample data if the null hypothesis is true. This p-value can be directly used to quantify risk. For instance, a p-value of 0.05 implies there’s a 5% risk of rejecting the null hypothesis when it’s actually true. This is invaluable in scenarios like product launches or changes in operational processes, where understanding the risk involved can be as crucial as the decision itself.

Here’s an example to help you understand the concept better.

The graph above serves as a graphical representation to help explain the concept of a ‘p-value’ and its role in quantifying risk in hypothesis testing. Here’s how to interpret the graph:

Elements of the Graph

• The curve represents a Standard Normal Distribution , which is often used to represent z-scores in hypothesis testing.
• The red-shaded area on the right represents the Rejection Region . It corresponds to a 5% risk ( α =0.05) of rejecting the null hypothesis when it is actually true. This is the area where, if your test statistic falls, you would reject the null hypothesis.
• The green-shaded area represents the Acceptance Region , with a 95% level of confidence. If your test statistic falls in this region, you would fail to reject the null hypothesis.
• The blue dashed line is the Critical Value (approximately 1.645 in this example). If your standardized test statistic (z-value) exceeds this point, you enter the rejection region, and your p-value becomes less than 0.05, leading you to reject the null hypothesis.

Relating to Risk Management

The p-value can be directly related to risk management. For example, if you’re considering implementing a new manufacturing process, the p-value quantifies the risk of that decision. A low p-value (less than α ) would mean that the risk of rejecting the null hypothesis (i.e., going ahead with the new process) when it’s actually true is low, thus indicating a lower risk in implementing the change.

Quality Control

In sectors like manufacturing, automotive, and logistics, maintaining a high level of quality is not just an option but a necessity. Hypothesis testing is often employed in quality assurance and control processes to test whether a certain process or product conforms to standards. For example, if a car manufacturing line claims its error rate is below 5%, hypothesis testing can confirm or disprove this claim based on a sample of products. This ensures that quality is not compromised and that stakeholders can trust the end product.

Resource Optimization

Resource allocation is a significant challenge for any organization. Hypothesis testing can be a valuable tool in determining where resources will be most effectively utilized. For instance, in a manufacturing setting, you might want to test whether a new piece of machinery significantly increases production speed. A hypothesis test could provide the statistical evidence needed to decide whether investing in more of such machinery would be a wise use of resources.

In the realm of research and development, hypothesis testing can be a game-changer. When developing a new product or process, you’ll likely have various theories or hypotheses. Hypothesis testing allows you to systematically test these, filtering out the less likely options and focusing on the most promising ones. This not only speeds up the innovation process but also makes it more cost-effective by reducing the likelihood of investing in ideas that are statistically unlikely to be successful.

In summary, hypothesis testing is a versatile tool that adds rigor, reduces risk, and enhances the decision-making and innovation processes across various sectors and functions.

This graphical representation makes it easier to grasp how the p-value is used to quantify the risk involved in making a decision based on a hypothesis test.

Step-by-Step Guide to Hypothesis Testing

To make this guide practical and helpful if you are new learning about the concept we will explain each step of the process and follow it up with an example of the method being applied to a manufacturing line, and you want to test if a new process reduces the average time it takes to assemble a product.

Step 1: State the Hypotheses

The first and foremost step in hypothesis testing is to clearly define your hypotheses. This sets the stage for your entire test and guides the subsequent steps, from data collection to decision-making. At this stage, you formulate two competing hypotheses:

Null Hypothesis ( H 0)

The null hypothesis is a statement that there is no effect or no difference, and it serves as the hypothesis that you are trying to test against. It’s the default assumption that any kind of effect or difference you suspect is not real, and is due to chance. Formulating a clear null hypothesis is crucial, as your statistical tests will be aimed at challenging this hypothesis.

In a manufacturing context, if you’re testing whether a new assembly line process has reduced the time it takes to produce an item, your null hypothesis ( H 0) could be:

H 0:”The new process does not reduce the average assembly time.”

Alternative Hypothesis ( Ha or H 1)

The alternative hypothesis is what you want to prove. It is a statement that there is an effect or difference. This hypothesis is considered only after you find enough evidence against the null hypothesis.

Continuing with the manufacturing example, the alternative hypothesis ( Ha ) could be:

Ha :”The new process reduces the average assembly time.”

Types of Alternative Hypothesis

Depending on what exactly you are trying to prove, the alternative hypothesis can be:

• Two-Sided : You’re interested in deviations in either direction (greater or smaller).
• One-Sided : You’re interested in deviations only in one direction (either greater or smaller).

Scenario: Reducing Assembly Time in a Car Manufacturing Plant

You are a continuous improvement manager at a car manufacturing plant. One of the assembly lines has been struggling with longer assembly times, affecting the overall production schedule. A new assembly process has been proposed, promising to reduce the assembly time per car. Before rolling it out on the entire line, you decide to conduct a hypothesis test to see if the new process actually makes a difference. Null Hypothesis ( H 0​) In this context, the null hypothesis would be the status quo, asserting that the new assembly process doesn’t reduce the assembly time per car. Mathematically, you could state it as: H 0:The average assembly time per car with the new process ≥ The average assembly time per car with the old process. Or simply: H 0​:”The new process does not reduce the average assembly time per car.” Alternative Hypothesis ( Ha ​ or H 1​) The alternative hypothesis is what you aim to prove — that the new process is more efficient. Mathematically, it could be stated as: Ha :The average assembly time per car with the new process < The average assembly time per car with the old process Or simply: Ha ​:”The new process reduces the average assembly time per car.” Types of Alternative Hypothesis In this example, you’re only interested in knowing if the new process reduces the time, making it a One-Sided Alternative Hypothesis .

Step 2: Determine the Significance Level ( α )

Once you’ve clearly stated your null and alternative hypotheses, the next step is to decide on the significance level, often denoted by α . The significance level is a threshold below which the null hypothesis will be rejected. It quantifies the level of risk you’re willing to accept when making a decision based on the hypothesis test.

What is a Significance Level?

The significance level, usually expressed as a percentage, represents the probability of rejecting the null hypothesis when it is actually true. Common choices for α are 0.05, 0.01, and 0.10, representing 5%, 1%, and 10% levels of significance, respectively.

• 5% Significance Level ( α =0.05) : This is the most commonly used level and implies that you are willing to accept a 5% chance of rejecting the null hypothesis when it is true.
• 1% Significance Level ( α =0.01) : This is a more stringent level, used when you want to be more sure of your decision. The risk of falsely rejecting the null hypothesis is reduced to 1%.
• 10% Significance Level ( α =0.10) : This is a more lenient level, used when you are willing to take a higher risk. Here, the chance of falsely rejecting the null hypothesis is 10%.

Continuing with the manufacturing example, let’s say you decide to set α =0.05, meaning you’re willing to take a 5% risk of concluding that the new process is effective when it might not be.

How to Choose the Right Significance Level?

Choosing the right significance level depends on the context and the consequences of making a wrong decision. Here are some factors to consider:

• Criticality of Decision : For highly critical decisions with severe consequences if wrong, a lower α like 0.01 may be appropriate.
• Resource Constraints : If the cost of collecting more data is high, you may choose a higher α to make a decision based on a smaller sample size.
• Industry Standards : Sometimes, the choice of α may be dictated by industry norms or regulatory guidelines.

By the end of Step 2, you should have a well-defined significance level that will guide the rest of your hypothesis testing process. This level serves as the cut-off for determining whether the observed effect or difference in your sample is statistically significant or not.

Continuing the Scenario: Reducing Assembly Time in a Car Manufacturing Plant

After formulating the hypotheses, the next step is to set the significance level ( α ) that will be used to interpret the results of the hypothesis test. This is a critical decision as it quantifies the level of risk you’re willing to accept when making a conclusion based on the test. Setting the Significance Level Given that assembly time is a critical factor affecting the production schedule, and ultimately, the company’s bottom line, you decide to be fairly stringent in your test. You opt for a commonly used significance level: α = 0.05 This means you are willing to accept a 5% chance of rejecting the null hypothesis when it is actually true. In practical terms, if you find that the p-value of the test is less than 0.05, you will conclude that the new process significantly reduces assembly time and consider implementing it across the entire line. Why α = 0.05 ? Industry Standard : A 5% significance level is widely accepted in many industries, including manufacturing, for hypothesis testing. Risk Management : By setting  α = 0.05 , you’re limiting the risk of concluding that the new process is effective when it may not be to just 5%. Balanced Approach : This level offers a balance between being too lenient (e.g., α=0.10) and too stringent (e.g., α=0.01), making it a reasonable choice for this scenario.

Step 3: Collect and Prepare the Data

After stating your hypotheses and setting the significance level, the next vital step is data collection. The data you collect serves as the basis for your hypothesis test, so it’s essential to gather accurate and relevant data.

Types of Data

Depending on your hypothesis, you’ll need to collect either:

• Quantitative Data : Numerical data that can be measured. Examples include height, weight, and temperature.
• Qualitative Data : Categorical data that represent characteristics. Examples include colors, gender, and material types.

Data Collection Methods

Various methods can be used to collect data, such as:

• Surveys and Questionnaires : Useful for collecting qualitative data and opinions.
• Observation : Collecting data through direct or participant observation.
• Experiments : Especially useful in scientific research where control over variables is possible.
• Existing Data : Utilizing databases, records, or any other data previously collected.

Sample Size

The sample size ( n ) is another crucial factor. A larger sample size generally gives more accurate results, but it’s often constrained by resources like time and money. The choice of sample size might also depend on the statistical test you plan to use.

Continuing with the manufacturing example, suppose you decide to collect data on the assembly time of 30 randomly chosen products, 15 made using the old process and 15 made using the new process. Here, your sample size n =30.

Data Preparation

Once data is collected, it often needs to be cleaned and prepared for analysis. This could involve:

• Removing Outliers : Outliers can skew the results and provide an inaccurate picture.
• Data Transformation : Converting data into a format suitable for statistical analysis.
• Data Coding : Categorizing or labeling data, necessary for qualitative data.

By the end of Step 3, you should have a dataset that is ready for statistical analysis. This dataset should be representative of the population you’re interested in and prepared in a way that makes it suitable for hypothesis testing.

With the hypotheses stated and the significance level set, you’re now ready to collect the data that will serve as the foundation for your hypothesis test. Given that you’re testing a change in a manufacturing process, the data will most likely be quantitative, representing the assembly time of cars produced on the line. Data Collection Plan You decide to use a Random Sampling Method for your data collection. For two weeks, assembly times for randomly selected cars will be recorded: one week using the old process and another week using the new process. Your aim is to collect data for 40 cars from each process, giving you a sample size ( n ) of 80 cars in total. Types of Data Quantitative Data : In this case, you’re collecting numerical data representing the assembly time in minutes for each car. Data Preparation Data Cleaning : Once the data is collected, you’ll need to inspect it for any anomalies or outliers that could skew your results. For example, if a significant machine breakdown happened during one of the weeks, you may need to adjust your data or collect more. Data Transformation : Given that you’re dealing with time, you may not need to transform your data, but it’s something to consider, depending on the statistical test you plan to use. Data Coding : Since you’re dealing with quantitative data in this scenario, coding is likely unnecessary unless you’re planning to categorize assembly times into bins (e.g., ‘fast’, ‘medium’, ‘slow’) for some reason. Example Data Points: Car_ID Process_Type Assembly_Time_Minutes 1 Old 38.53 2 Old 35.80 3 Old 36.96 4 Old 39.48 5 Old 38.74 6 Old 33.05 7 Old 36.90 8 Old 34.70 9 Old 34.79 … … … The complete dataset would contain 80 rows: 40 for the old process and 40 for the new process.

Step 4: Conduct the Statistical Test

After you have your hypotheses, significance level, and collected data, the next step is to actually perform the statistical test. This step involves calculations that will lead to a test statistic, which you’ll then use to make your decision regarding the null hypothesis.

Choose the Right Test

The first task is to decide which statistical test to use. The choice depends on several factors:

• Type of Data : Quantitative or Qualitative
• Sample Size : Large or Small
• Number of Groups or Categories : One-sample, Two-sample, or Multiple groups

For instance, you might choose a t-test for comparing means of two groups when you have a small sample size. Chi-square tests are often used for categorical data, and ANOVA is used for comparing means across more than two groups.

Calculation of Test Statistic

Once you’ve chosen the appropriate statistical test, the next step is to calculate the test statistic. This involves using the sample data in a specific formula for the chosen test.

Obtain the p-value

After calculating the test statistic, the next step is to find the p-value associated with it. The p-value represents the probability of observing the given test statistic if the null hypothesis is true.

• A small p-value (< α ) indicates strong evidence against the null hypothesis, so you reject the null hypothesis.
• A large p-value (> α ) indicates weak evidence against the null hypothesis, so you fail to reject the null hypothesis.

Make the Decision

You now compare the p-value to the predetermined significance level ( α ):

• If p < α , you reject the null hypothesis in favor of the alternative hypothesis.
• If p > α , you fail to reject the null hypothesis.

In the manufacturing case, if your calculated p-value is 0.03 and your α is 0.05, you would reject the null hypothesis, concluding that the new process effectively reduces the average assembly time.

By the end of Step 4, you will have either rejected or failed to reject the null hypothesis, providing a statistical basis for your decision-making process.

Now that you have collected and prepared your data, the next step is to conduct the actual statistical test to evaluate the null and alternative hypotheses. In this case, you’ll be comparing the mean assembly times between cars produced using the old and new processes to determine if the new process is statistically significantly faster. Choosing the Right Test Given that you have two sets of independent samples (old process and new process), a Two-sample t-test for Equality of Means seems appropriate for comparing the average assembly times. Preparing Data for Minitab Firstly, you would prepare your data in an Excel sheet or CSV file with one column for the assembly times using the old process and another column for the assembly times using the new process. Import this file into Minitab. Steps to Perform the Two-sample t-test in Minitab Open Minitab : Launch the Minitab software on your computer. Import Data : Navigate to File > Open and import your data file. Navigate to the t-test Menu : Go to Stat > Basic Statistics > 2-Sample t... . Select Columns : In the dialog box, specify the columns corresponding to the old and new process assembly times under “Sample 1” and “Sample 2.” Options : Click on Options and make sure that you set the confidence level to 95% (which corresponds to α = 0.05 ). Run the Test : Click OK to run the test. In this example output, the p-value is 0.0012, which is less than the significance level α = 0.05 . Hence, you would reject the null hypothesis. The t-statistic is -3.45, indicating that the mean of the new process is statistically significantly less than the mean of the old process, which aligns with your alternative hypothesis. Showing the data displayed as a Box plot in the below graphic it is easy to see the new process is statistically significantly better.

Why do a Hypothesis test?

You might ask, after all this why do a hypothesis test and not just look at the averages, which is a good question. While looking at average times might give you a general idea of which process is faster, hypothesis testing provides several advantages that a simple comparison of averages doesn’t offer:

Statistical Significance

Account for Random Variability : Hypothesis testing considers not just the averages, but also the variability within each group. This allows you to make more robust conclusions that account for random chance.

Quantify the Evidence : With hypothesis testing, you obtain a p-value that quantifies the strength of the evidence against the null hypothesis. A simple comparison of averages doesn’t provide this level of detail.

Control Type I Error : Hypothesis testing allows you to control the probability of making a Type I error (i.e., rejecting a true null hypothesis). This is particularly useful in settings where the consequences of such an error could be costly or risky.

Quantify Risk : Hypothesis testing provides a structured way to make decisions based on a predefined level of risk (the significance level, α ).

Decision-making Confidence

Objective Decision Making : The formal structure of hypothesis testing provides an objective framework for decision-making. This is especially useful in a business setting where decisions often have to be justified to stakeholders.

Replicability : The statistical rigor ensures that the results are replicable. Another team could perform the same test and expect to get similar results, which is not necessarily the case when comparing only averages.

Additional Insights

Understanding of Variability : Hypothesis testing often involves looking at measures of spread and distribution, not just the mean. This can offer additional insights into the processes you’re comparing.

Basis for Further Analysis : Once you’ve performed a hypothesis test, you can often follow it up with other analyses (like confidence intervals for the difference in means, or effect size calculations) that offer more detailed information.

In summary, while comparing averages is quicker and simpler, hypothesis testing provides a more reliable, nuanced, and objective basis for making data-driven decisions.

Step 5: Interpret the Results and Make Conclusions

Having conducted the statistical test and obtained the p-value, you’re now at a stage where you can interpret these results in the context of the problem you’re investigating. This step is crucial for transforming the statistical findings into actionable insights.

Interpret the p-value

The p-value you obtained tells you the significance of your results:

• Low p-value ( p < α ) : Indicates that the results are statistically significant, and it’s unlikely that the observed effects are due to random chance. In this case, you generally reject the null hypothesis.
• High p-value ( p > α ) : Indicates that the results are not statistically significant, and the observed effects could well be due to random chance. Here, you generally fail to reject the null hypothesis.

Relate to Real-world Context

You should then relate these statistical conclusions to the real-world context of your problem. This is where your expertise in your specific field comes into play.

In our manufacturing example, if you’ve found a statistically significant reduction in assembly time with a p-value of 0.03 (which is less than the α level of 0.05), you can confidently conclude that the new manufacturing process is more efficient. You might then consider implementing this new process across the entire assembly line.

Make Recommendations

Based on your conclusions, you can make recommendations for action or further study. For example:

• Implement Changes : If the test results are significant, consider making the changes on a larger scale.
• Further Research : If the test results are not clear or not significant, you may recommend further studies or data collection.
• Review Methodology : If you find that the results are not as expected, it might be useful to review the methodology and see if the test was conducted under the right conditions and with the right test parameters.

Document the Findings

Lastly, it’s essential to document all the steps taken, the methodology used, the data collected, and the conclusions drawn. This documentation is not only useful for any further studies but also for auditing purposes or for stakeholders who may need to understand the process and the findings.

By the end of Step 5, you’ll have turned the raw statistical findings into meaningful conclusions and actionable insights. This is the final step in the hypothesis testing process, making it a complete, robust method for informed decision-making.

You’ve successfully conducted the hypothesis test and found strong evidence to reject the null hypothesis in favor of the alternative: The new assembly process is statistically significantly faster than the old one. It’s now time to interpret these results in the context of your business operations and make actionable recommendations. Interpretation of Results Statistical Significance : The p-value of 0.0012 is well below the significance level of = 0.05   α = 0.05 , indicating that the results are statistically significant. Practical Significance : The boxplot and t-statistic (-3.45) suggest not just statistical, but also practical significance. The new process appears to be both consistently and substantially faster. Risk Assessment : The low p-value allows you to reject the null hypothesis with a high degree of confidence, meaning the risk of making a Type I error is minimal. Business Implications Increased Productivity : Implementing the new process could lead to an increase in the number of cars produced, thereby enhancing productivity. Cost Savings : Faster assembly time likely translates to lower labor costs. Quality Control : Consider monitoring the quality of cars produced under the new process closely to ensure that the speedier assembly does not compromise quality. Recommendations Implement New Process : Given the statistical and practical significance of the findings, recommend implementing the new process across the entire assembly line. Monitor and Adjust : Implement a control phase where the new process is monitored for both speed and quality. This could involve additional hypothesis tests or control charts. Communicate Findings : Share the results and recommendations with stakeholders through a formal presentation or report, emphasizing both the statistical rigor and the potential business benefits. Review Resource Allocation : Given the likely increase in productivity, assess if resources like labor and parts need to be reallocated to optimize the workflow further.

By following this step-by-step guide, you’ve journeyed through the rigorous yet enlightening process of hypothesis testing. From stating clear hypotheses to interpreting the results, each step has paved the way for making informed, data-driven decisions that can significantly impact your projects, business, or research.

Hypothesis testing is more than just a set of formulas or calculations; it’s a holistic approach to problem-solving that incorporates context, statistics, and strategic decision-making. While the process may seem daunting at first, each step serves a crucial role in ensuring that your conclusions are both statistically sound and practically relevant.

• McKenzie, C.R., 2004. Hypothesis testing and evaluation .  Blackwell handbook of judgment and decision making , pp.200-219.
• Park, H.M., 2015. Hypothesis testing and statistical power of a test.
• Eberhardt, L.L., 2003. What should we do about hypothesis testing? .  The Journal of wildlife management , pp.241-247.

Q: What is hypothesis testing in the context of Lean Six Sigma?

A: Hypothesis testing is a statistical method used in Lean Six Sigma to determine whether there is enough evidence in a sample of data to infer that a certain condition holds true for the entire population. In the Lean Six Sigma process, it’s commonly used to validate the effectiveness of process improvements by comparing performance metrics before and after changes are implemented. A null hypothesis ( H 0 ​ ) usually represents no change or effect, while the alternative hypothesis ( H 1 ​ ) indicates a significant change or effect.

Q: How do I determine which statistical test to use for my hypothesis?

A: The choice of statistical test for hypothesis testing depends on several factors, including the type of data (nominal, ordinal, interval, or ratio), the sample size, the number of samples (one sample, two samples, paired), and whether the data distribution is normal. For example, a t-test is used for comparing the means of two groups when the data is normally distributed, while a Chi-square test is suitable for categorical data to test the relationship between two variables. It’s important to choose the right test to ensure the validity of your hypothesis testing results.

Q: What is a p-value, and how does it relate to hypothesis testing?

A: A p-value is a probability value that helps you determine the significance of your results in hypothesis testing. It represents the likelihood of obtaining a result at least as extreme as the one observed during the test, assuming that the null hypothesis is true. In hypothesis testing, if the p-value is lower than the predetermined significance level (commonly α = 0.05 ), you reject the null hypothesis, suggesting that the observed effect is statistically significant. If the p-value is higher, you fail to reject the null hypothesis, indicating that there is not enough evidence to support the alternative hypothesis.

Q: Can you explain Type I and Type II errors in hypothesis testing?

A: Type I and Type II errors are potential errors that can occur in hypothesis testing. A Type I error, also known as a “false positive,” occurs when the null hypothesis is true, but it is incorrectly rejected. It is equivalent to a false alarm. On the other hand, a Type II error, or a “false negative,” happens when the null hypothesis is false, but it is erroneously failed to be rejected. This means a real effect or difference was missed. The risk of a Type I error is represented by the significance level ( α ), while the risk of a Type II error is denoted by β . Minimizing these errors is crucial for the reliability of hypothesis tests in continuous improvement projects.

Daniel Croft

Hi im Daniel continuous improvement manager with a Black Belt in Lean Six Sigma and over 10 years of real-world experience across a range sectors, I have a passion for optimizing processes and creating a culture of efficiency. I wanted to create Learn Lean Siigma to be a platform dedicated to Lean Six Sigma and process improvement insights and provide all the guides, tools, techniques and templates I looked for in one place as someone new to the world of Lean Six Sigma and Continuous improvement.

Free Lean Six Sigma Templates

Improve your Lean Six Sigma projects with our free templates. They're designed to make implementation and management easier, helping you achieve better results.

Was this helpful?

• Certified Six Sigma Green Belt (CSSGB™)
• Certified Six Sigma Black Belt (CSSBB™)
• Certified Six Sigma Master Black Belt (CSSMBB™)
• Certified Six Sigma Champion (CSSC™)
• Certified Six Sigma Deployment Leader (CSSDL™)
• Certified Six Sigma Yellow Belt (CSSYB™)
• Certified Six Sigma Trainer (CSSTRA™)
• Certified Six Sigma Coach (CSSCOA™)
• Register Your Six Sigma Certification Program
• International Scrum Institute™
• International DevOps Certification Academy™
• International Organization for Project Management (IO4PM™)
• International Software Test Institute™
• International MBA Institute™
• Your Blog (US Army Personnel Selected Six Sigma Institute™)
• Our Industry Review and Feedback
• Our Official Recognition and Industry Clients
• Our Corporate Partners Program
• Frequently Asked Questions (FAQ)
• Shareable Digital Badge And Six Sigma Certifications Validation Registry (NEW)
• Recommend International Six Sigma Institute™ To Friends
• Introducing: World's First & Only Six Sigma AI Assistant (NEW)
• Your Free Six Sigma Book
• Your Free Premium Six Sigma Training
• Your Sample Six Sigma Certification Test Questions
• Your Free Six Sigma Events
• Terms and Conditions
• Privacy Policy

Six Sigma Hypothesis Testing: Results with P-Value & Data

Hypothesis testing is crucial in Six Sigma as it provides a statistical framework to analyze process improvements, measure project progress, and make data-driven decisions. By using hypothesis testing, Six Sigma practitioners can effectively determine whether changes made to a process have resulted in meaningful improvements or not, thus ensuring strategic decision-making based on evidence.

Six Sigma DMAIC - Analyze Phase - Hypothesis Testing

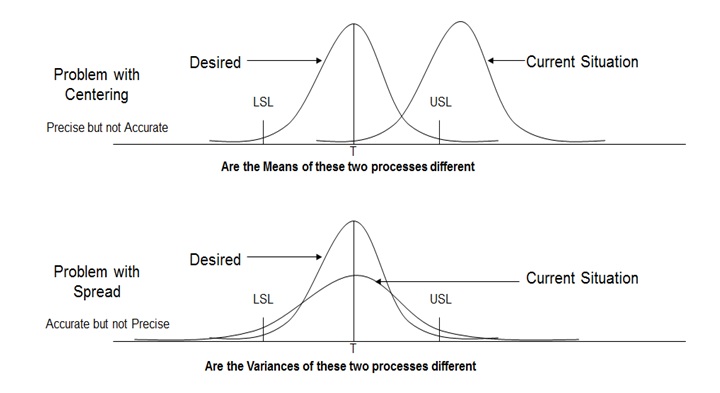
What is the difference that can be detected using Hypothesis Testing?

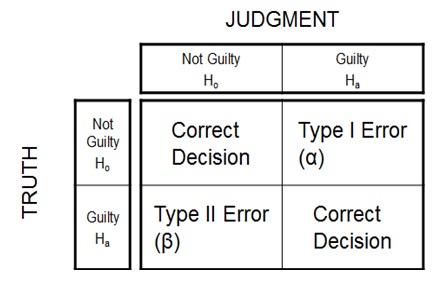
• Step 1: Determine appropriate Hypothesis test
• Step 2: State the Null Hypothesis Ho and Alternate Hypothesis Ha
• Step 3: Calculate Test Statistics / P-value against table value of test statistic
• Step 4: Interpret results – Accept or reject Ho
• Ho = Null Hypothesis – There is No statistically significant difference between the two groups
• Ha = Alternate Hypothesis – There is statistically significant difference between the two groups

P Value – Also known as Probability value, it is a statistical measure which indicates the probability of making an α error. The value ranges between 0 and 1. We normally work with 5% alpha risk, a p value lower than 0.05 means that we reject the Null hypothesis and accept alternate hypothesis.

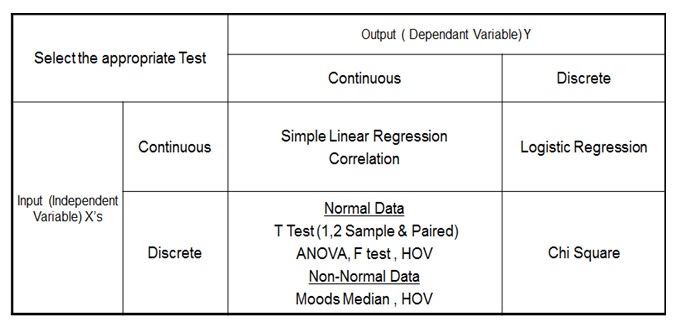
What is P-Value in Six Sigma?

Six sigma hypothesis: null and alternative.

It's crucial to understand that both hypotheses play complementary roles in hypothesis testing. While the null hypothesis anchors the current state or standard processes, the alternative hypothesis serves as a beacon for evaluating potential enhancements or variances resulting from process improvements or changes. When these two hypotheses are utilized effectively, they provide a structured framework for detailed analysis and decision-making.

Tools for Six Sigma Hypothesis Testing

Difference analysis in six sigma hypothesis testing.

Applying a t-test for comparing means or another suitable hypothesis testing method will help evaluate whether the decrease from 10 minutes to 8 minutes is meaningful or just due to chance. It allows decision-makers to make informed choices based on statistical test inferences rather than relying solely on anecdotal evidence or individual perceptions.

Deciding Hypothesis Validity in Six Sigma

This decision-making process plays a pivotal role in organizational decision-making because it guides leaders in determining whether observed changes are truly beneficial or merely due to chance. In essence, what we are doing here is looking for hard evidence through data analysis—evidence that supports our belief about positive changes resulting from specific actions taken within our processes.

Enhancing Precision via Reduction of Variation

Practical applications of hypothesis testing in six sigma.

All these scenarios underscore the practical relevance of hypothesis testing in enabling organizations to make informed decisions and allocate resources effectively based on tangible evidence rather than intuition or assumptions.

Frequently Asked Questions about Six Sigma Hypothesis Testing

What are some common types of hypothesis tests used in six sigma projects, how does hypothesis testing fit into the six sigma methodology, how do you determine the significance level and power of a hypothesis test in six sigma, what are some practical examples or case studies where hypothesis testing has been applied successfully in a six sigma project.

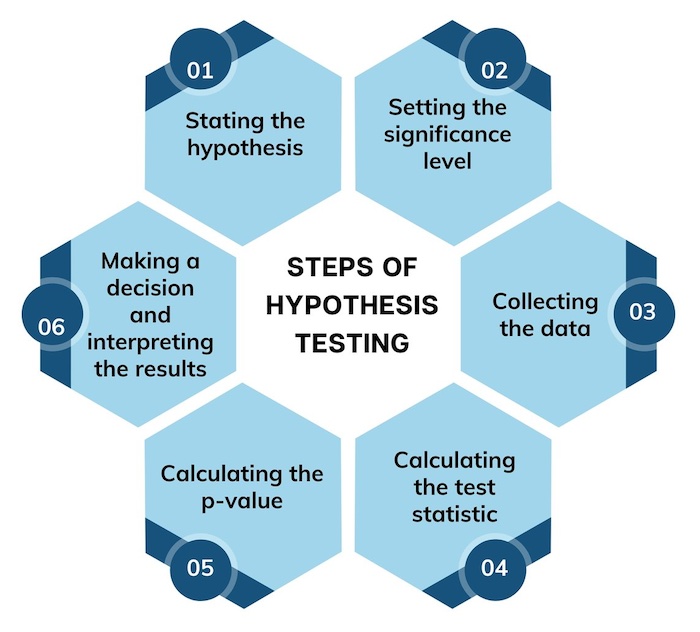
What are the key steps involved in conducting hypothesis testing in Six Sigma?

What is the purpose of hypothesis testing in six sigma, in the dmaic method, which stage identifies with the confirmation and testing the statistical solution, project y is continuous and x is discrete to validate variance between subgroups. what does this mean, which hypothesis test will you perform when the y is continuous normal and x is discrete. what does this this mean, what is sigma test, what is beta testing is six sigma, what null hypothesis in six sigma, recap of six sigma hypothesis testing with p-values.

Mastering Six Sigma hypothesis testing, including the interpretation of P-values, is a skill that can significantly enhance one's ability to drive process improvements and minimize variation. The recap of these testing techniques serves as a valuable reminder of the precision required in decision-making within the Six Sigma framework. Whether you're initiating a project or refining existing processes, the insights gained from comprehending P-values contribute to the success of your continuous improvement initiatives.

Your Six Sigma Training Table of Contents

We guarantee that your free online training will make you pass your six sigma certification exam.

THE ONLY BOOK. YOU CAN SIMPLY LEARN SIX SIGMA.

YOUR SIX SIGMA REVEALED 2ND EDITION IS NOW READY. CLICK BOOK COVER FOR FREE DOWNLOAD...

Hypothesis Testing

Hypothesis Testing in Lean Six Sigma

One of the essential tools in the Lean Six Sigma toolkit is hypothesis testing. Hypothesis testing is crucial in the Define-Measure-Analyze-Improve-Control (DMAIC) cycle, helping organizations make data-driven decisions and achieve continuous improvement. This article will explore the significance of hypothesis testing in Lean Six Sigma, its key concepts, and practical applications.

Understanding Hypothesis Testing

Hypothesis testing is a statistical method used to determine whether there is a significant difference between two or more sets of data. In the context of Lean Six Sigma, it is primarily used to assess the impact of process changes or improvements. The process of hypothesis testing involves formulating two competing hypotheses:

• Null Hypothesis (H0):   This hypothesis assumes that there is no significant difference or effect. It represents the status quo or the current state of the process.
• Alternative Hypothesis (Ha) or (H1):   This hypothesis suggests that there is a significant difference or effect resulting from process changes or improvements.

The goal of hypothesis testing is to collect and analyze data to either accept or reject the null hypothesis in favor of the alternative hypothesis.

Key Steps in Hypothesis Testing in Lean Six Sigma

• Define the Problem: The first step in Lean Six Sigma’s DMAIC cycle is clearly defining the problem. This involves understanding the process, identifying the problem’s scope, and setting measurable goals for improvement.
• Formulate Hypotheses: Once the problem is defined, the next step is to formulate the null and alternative hypotheses. This step is crucial as it sets the foundation for the hypothesis testing process.
• Collect Data: Data collection is critical to hypothesis testing. Lean Six Sigma practitioners gather relevant data using various methods, ensuring the data is accurate, representative, and sufficient for analysis.
• Analyze Data: Statistical analysis is the heart of hypothesis testing. Different statistical tests are used depending on the data type and the analysis objectives. Common tests include t-tests, chi-square tests, and analysis of variance (ANOVA) .
• Determine Significance Level: A significance level (alpha) is set to determine the threshold for accepting or rejecting the null hypothesis in hypothesis testing. Common significance levels are 0.05 and 0.01, representing a 5% and 1% chance of making a Type I error, respectively.
• Calculate Test Statistic: The test statistic is computed from the collected data and compared to a critical value or a p-value to determine its significance.
• Make a Decision: Based on the test statistic and significance level, a decision is made either to reject the null hypothesis in favor of the alternative hypothesis or to fail to reject the null hypothesis.
• Draw Conclusions: The final step involves drawing conclusions based on the decision made in step 7. These conclusions inform the next steps in the Lean Six Sigma DMAIC cycle, whether it be process improvement, optimization, or control.

Practical Applications of Hypothesis Testing in Lean Six Sigma

• Process Improvement: Hypothesis testing is often used to assess whether process improvements, such as changes in machinery, materials, or procedures, lead to significant enhancements in process performance.
• Root Cause Analysis: Lean Six Sigma practitioners employ hypothesis testing to identify the root causes of process defects or variations, helping organizations address the underlying issues effectively.
• Product Quality Control: Manufacturers use hypothesis testing to ensure the quality of products meets predefined standards and specifications, reducing defects and customer complaints.
• Cost Reduction: By testing hypotheses related to cost reduction initiatives, organizations can determine whether cost-saving measures are effective and sustainable.
• Customer Satisfaction: Hypothesis testing can be applied to customer feedback data to determine if changes in products or services result in increased customer satisfaction.

Six Sigma Green Belt vs Six Sigma Black Belt in Hypothesis Testing

Six Sigma Black Belts and Six Sigma Green Belts both use hypothesis testing as a critical tool in process improvement projects, but there are differences in their roles and responsibilities, which influence how they employ hypothesis testing:

1. Project Leadership and Complexity:

• Black Belts : Black Belts typically lead larger and more complex improvement projects. They are responsible for selecting projects that significantly impact the organization’s strategic goals. Hypothesis testing for Black Belts often involves multifaceted analyses, intricate data collection strategies, and a deeper understanding of statistical techniques.
• Green Belts : Green Belts usually work on smaller-scale projects or support Black Belts on larger projects. Their projects may have a narrower focus and involve less complex hypothesis testing than Black Belts.

2. Statistical Expertise:

• Black Belts : Black Belts are expected to have a higher level of statistical expertise. They are often skilled in advanced statistical methods and can handle complex data analysis. They might use more advanced statistical techniques such as multivariate analysis, design of experiments (DOE), or regression modeling.
• Green Belts : Green Belts have a solid understanding of basic statistical methods and hypothesis testing but may not have the same depth of expertise as Black Belts. They typically use simpler statistical tools for hypothesis testing.

3. Project Oversight and Coaching:

• Black Belts : Black Belts often mentor or coach Green Belts and team members. They guide and oversee multiple projects simultaneously, ensuring that the right tools and methods, including hypothesis testing, are applied effectively.
• Green Belts : Green Belts focus primarily on their own project work but may receive guidance and support from Black Belts. They contribute to projects led by Black Belts and assist in data collection and analysis.

4. Strategic Impact:

• Black Belts : Black Belts work on projects that are closely aligned with the organization’s strategic goals. They are expected to deliver significant financial and operational benefits. Hypothesis testing for Black Belts may have a direct impact on strategic decision-making.
• Green Belts : Green Belts work on projects that often contribute to departmental or functional improvements. While their projects can still have a substantial impact, they may not be as closely tied to the organization’s overall strategic direction.

5. Reporting and Presentation:

• Black Belts : Black Belts are typically responsible for presenting project findings and recommendations to senior management. They must effectively communicate the results of hypothesis testing and their implications for the organization.
• Green Belts : Green Belts may present their findings to their immediate supervisors or project teams but may not have the same level of exposure to senior management as Black Belts.

Six Sigma Black Belts and Green Belts both use hypothesis testing, but Black Belts tend to handle more complex, strategically significant projects, often involving advanced statistical methods. They also play a coaching and leadership role within the organization, whereas Green Belts primarily focus on their own projects and may support Black Belts in larger initiatives. The level of statistical expertise, project complexity, and strategic impact are key factors that differentiate how each role uses hypothesis testing.

Drawbacks to Using Hypothesis Testing During a Six Sigma Project

It’s important to recognize that while hypothesis testing is a valuable tool, it is not without its challenges and limitations. Lets delve into some of the drawbacks and complexities associated with employing hypothesis testing within the context of Six Sigma projects.

Data Quality and Availability: One fundamental challenge lies in the quality and accessibility of data. Hypothesis testing relies heavily on having accurate and pertinent data at hand. Obtaining high-quality data can sometimes be a formidable task, and gaps or inaccuracies in the data can jeopardize the reliability of the analysis.

Assumptions and Simplifications: Many hypothesis tests are built upon certain assumptions about the data, such as adherence to specific statistical distributions or characteristics. These assumptions, when violated, can compromise the accuracy and validity of the test results. Real-world data often exhibits complexity that may not neatly conform to these assumptions.

Sample Size Considerations: The effectiveness of a hypothesis test is significantly influenced by the sample size. Smaller sample sizes may not possess the statistical power necessary to detect meaningful differences, potentially leading to erroneous conclusions. Conversely, larger sample sizes may unearth statistically significant differences that may not have practical significance.

Type I and Type II Errors: Hypothesis testing necessitates a careful balance between Type I errors (incorrectly rejecting a true null hypothesis) and Type II errors (failing to reject a false null hypothesis). The choice of the significance level (alpha) directly impacts the trade-off between these errors, making it crucial to select an appropriate alpha level for the specific context.

Complex Interactions: Real-world processes often involve intricate interactions between multiple variables and factors. Hypothesis testing, by design, simplifies these interactions, potentially leading to an oversimplified understanding of the process dynamics. Neglecting these interactions can result in inaccurate conclusions and ineffective process improvements.

Time and Resources: Hypothesis testing can be resource-intensive and time-consuming, especially when dealing with extensive datasets or complex statistical analyses. The process requires allocation of resources for data collection, analysis, and interpretation. Striking the right balance between the benefits of hypothesis testing and the resources invested is a consideration in Six Sigma projects.

Overemphasis on Statistical Significance: There is a risk of becoming overly focused on achieving statistical significance. While statistical significance holds importance, it does not always translate directly into practical significance or tangible business value. A fixation on p-values and statistical significance can sometimes lead to a myopic view of the broader context.

Contextual Factors: Hypothesis testing, on its own, does not encompass all contextual elements that may influence process performance. Factors such as external market conditions, customer preferences, and regulatory changes may not be adequately accounted for through hypothesis testing alone. Complementing hypothesis testing with qualitative analysis and a holistic understanding of the process environment is essential.

Hypothesis testing is a valuable tool in Six Sigma projects, but it is vital to acknowledge its limitations and complexities. Practitioners should exercise caution, ensuring that hypothesis testing is applied judiciously and that its results are interpreted within the broader framework of organizational goals. Success in Six Sigma projects often hinges on blending statistical rigor with practical wisdom.

Hypothesis testing is a fundamental tool in the Lean Six Sigma methodology, enabling organizations to make data-driven decisions, identify process improvements, and enhance overall efficiency and quality. When executed correctly, hypothesis testing empowers businesses to achieve their goals, reduce defects, cut costs, and, ultimately, deliver better products and services to their customers. By integrating hypothesis testing into the DMAIC cycle, Lean Six Sigma practitioners can drive continuous improvement and ensure the long-term success of their organizations.

These tools and techniques are not mutually exclusive, and their selection depends on the problem’s nature, the process’s complexity, and the data available. Six Sigma practitioners, including Green Belts and Black Belts, are trained to use these tools effectively to drive meaningful improvements during the Improve stage of DMAIC.

Lean Six Sigma Green Belt Certification

Lean Six Sigma Black Belt Certification

Six Sigma Body of Knowledge

View All Six Sigma Certifications

Six Sigma Resource Center

• All Certifications
• Accessibility

Connect With Us

Copyright © 2022 MSI. All Rights Reserved.

Take advantage of your time, International Six Sigma Inc. offers both Instructor-led Live Virtual classes as well as Online Self-Paced training . Enroll Today!

Hypothesis Testing

Hypothesis testing is a statistical method for determining whether data sufficiently supports a specific hypothesis. It’s a vital skill when analyzing business processes to identify and solve problems. This course will dive deep into Hypothesis testing to enhance your analytical skills.

We’ll introduce you to Hypothesis Testing and explore the Null and Alternative Hypotheses. We’ll explain the use of p-values in decision-making, the Analysis Roadmap, and how to apply the Test Selection Matrix. You’ll also gain an understanding of the two types of errors that occur when using these concepts and how to navigate them.

What you’ll learn

• Hypothesis Testing Concepts
• Null and Alternative Hypotheses
• The use of p-Values
• The Analysis Roadmap and Test Selection Matrix
• The 2 types of Errors involved with Hypothesis Testing

Hypothesis Testing Online Training Program Includes

• 30-day access to our Learning Management System
• Modern player with transcription of the narration , adjustable playback speed , full-screen and more
• Access to the training manual in electronic format
• A quiz test
• Hypothesis Testing Certification upon completion
• Ability to upgrade at a later date to the our other online programs

Online Hypothesis Testing Program Requirements

• A computer, tablet or smartphone with internet connection

Pricing: $29.00

Once we process your payment we will provide you with your personal online training account.

Note: There are no refunds once the program has been started or 7 days after purchase.

Contact us  if you have additional questions.

At home or workplace, we have you covered

Training Options

More than 500 locations

Classroom Training

Learn anytime, anywhere

Online Training

Live instructor-led training

Webinar Training

Customized training programs

On-site Training

Accelerated training programs

Blended Training

For streamlined business plans

Operational Excellence

Exclusive consulting services

Consulting Services

Fully customized programs

Group/Corporate Training

International six sigma inc. accreditation & affiliations.

Email: [email protected] Toll Free in the US: (866) 409-1363

Courses / Training

How to Optimize the Value of Hypothesis Testing

Updated: August 18, 2024 by Ken Feldman

Hypothesis testing is a branch of statistics in which, using data from a sample, an inference is made about a population parameter or a population probability distribution . 

Let’s look at the purpose of hypothesis testing, the underlying statistical concepts, the importance of using hypothesis testing, and some best practices for optimizing the value of the technique.

Overview: What is hypothesis testing? 

Hypothesis testing in statistics is a way for you to test the results of an experiment to see if you have meaningful results. The outcome of your hypothesis test will tell you whether your results are caused by pure chance or not. If your results are due to pure chance, then you will have a difficult time replicating or repeating them. But, if your results were due to something significant happening, you can use that knowledge to repeat the results.

Hypothesis testing applies to all forms of statistical inquiry. For example, it can be used to determine whether there are differences between population parameters or to gain an understanding about slopes of regression lines or equality of probability distributions.

The process for completing a hypothesis test

First, a hypothesis statement and assumption is made about the population parameter or probability distribution. This initial statement is called the null hypothesis and is denoted by H o. An alternative or alternate hypothesis (denoted with Ha ), is then stated, which will be the opposite of the null hypothesis. 

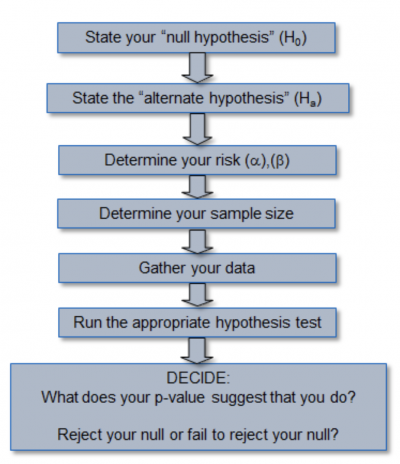
The hypothesis testing process and analysis involves using sample data to determine whether or not you can be statistically confident that you can reject the H o. If the H o is rejected, the statistical conclusion is that the alternative or alternate hypothesis Ha is true.

Since you’re using sample data to make your inferences about the population, there’s a risk that you’ll make an error. You can choose the level of risk you’re willing to accept for this error. In the case of the null hypothesis, we can make one of two errors.

• Type 1 , or alpha error : An alpha error is when you mistakenly reject the null and believe that something significant happened when it did not. In other words, you might believe that the means of the two populations are different when they aren’t. You can pick your risk of being wrong to be 1%, 5%, 10%, or any other reasonable value.
• Type 2, or beta error: A beta error is when you fail to reject the null when you should have. In this case, you missed something significant and failed to take action. This risk typically runs in the range of 80% to 90%, or again, any other reasonable value.

The next step would be to determine the appropriate sample size you would need to be able to rely on the statistical validity of your results. Then, go out and collect your data.

You will then need to decide what is the appropriate statistical test for the type of data and hypothesis you’re testing. Using a statistical software package, you’ll get a multitude of numerical results. One you can focus on is something called the p-value . The p-value is your calculated risk of making an alpha error, or claiming success when there really wasn’t any. You will likely require the advice and guidance from a Lean Six Sigma Black Belt or Master Black Belt to sort all of this out.

Finally, you’ll need to make a decision to reject or not reject the null hypothesis. Your decision is made by comparing the alpha value (your assumed risk) with the p-value (actual risk). If the actual risk is lower than your assumed risk, you can feel comfortable in rejecting the null and claiming something has happened. But if the actual risk is higher than your assumed risk, you will be taking a bigger risk than you want by rejecting the null.

3 benefits of hypothesis testing

Hypothesis testing is a statistical technique for making decisions about whether the changes in your process are a result of chance or a result of some improvements you made. Here’s why you want to use hypothesis testing.

1. Statistical assurance of determining differences between population parameters

Just looking at the mathematical difference between the means of two samples and making a decision is woefully inadequate. By statistically testing the null hypothesis, you will have more confidence in any inferences you want to make about populations based on your samples.

2. Statistically-based estimation of the probability of a population distribution

Many statistical tests require assumptions of specific distributions. Many of these tests assume that the population follows the normal distribution . If it doesn’t, the test may be invalid.  

3. Assess the strength of your conclusions as to what to do with the null hypothesis

Hypothesis testing calculations will provide some relative strength to your decisions as to whether you reject or fail to reject the null hypothesis.

Why is hypothesis testing important to understand?

The interpretation of the statistics relative to the null hypothesis is what’s important.

Properly write the null hypothesis to properly capture what you are seeking to prove

The null is always written in the same format. That is, the lack of difference or some other condition. The alternative hypothesis can be written in three formats depending on what you want to prove. 

Frame your statement and select an appropriate alpha risk

You don’t want to place too big of a hurdle or burden on your decision-making relative to action on the null hypothesis by selecting an alpha value that is too high or too low.

There are decision errors when deciding on how to respond to the null hypothesis

Since your decision relative to rejecting or not rejecting the null is based on statistical calculations, it’s important to understand how that decision works. 

An industry example of using hypothesis testing

The new director of marketing just completed the rollout of a new marketing campaign targeting the Hispanic market. Early indications showed that the campaign was successful in increasing sales in the Hispanic market. 

He came to that conclusion by comparing a sample of sales prior to the campaign and current sales after implementation of the campaign. He was anxious to proudly tell his boss how successful the campaign was. But, he decided to first check with his Lean Six Sigma Black Belt to see whether she agreed with his conclusion.

The Black Belt first asked the director his tolerance for risk of being wrong by telling the boss the campaign was successful when in fact, it wasn’t. That was the alpha value. The Director picked 5% since he was new and didn’t want to make a false claim so early in his career. He also picked 20% as his beta value.  

When the Black Belt was done analyzing the data, she found out that the p-value was 15%.  That meant if the director told the VP the campaign worked, there was a 15% chance he would be wrong and that the campaign probably needed some revising. Since he was only willing to be wrong 5% of the time, the decision was to not reject the null since his 5% assumed risk was less than the 15% actual risk.

3 best practices when thinking about hypothesis testing 

Using hypothesis testing to help make better data-driven decisions requires that you properly adhere to the testing procedure. 

1. Always use the proper nomenclature when stating the null and alternative hypotheses 

The null will always be in the form of decisions regarding the population, not the sample. For example, the null and alternate hypotheses for testing the difference between two means is written as:

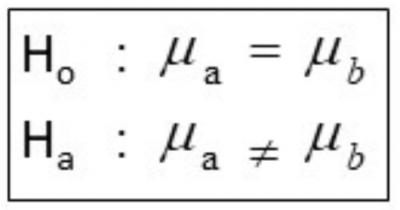
Note that you use mu (population average) as the nomenclature for the mean, not Xbar (sample average). You are not interested in whether the sample means are different since you already have those calculations. You are interested in if the means of the two populations the samples came from are different. 

2. Select an appropriate sample size

The statistics and final results will depend on you determining the appropriate sample size, and then collecting the data in an appropriate manner. Use statistics to determine sample size, not intuition. 

3. Pick a reasonable alpha risk so you’re not always failing to reject the null hypothesis

Being too cautious will lead you to make beta errors, and you’ll never learn anything about your population data. 

Frequently Asked Questions (FAQ) about hypothesis testing

What form should the null hypothesis be written in.

The null hypothesis should always be in the form of no difference, or zero, and always refer to the state of the population, not the sample. 

What is an alpha error? 

An alpha error, or Type 1 error, is rejecting the null hypothesis and claiming a significant event has occurred when, in fact, that is not true and the null should not have been rejected.

How do I use the alpha error and p-value to decide on what decision I should make about the null hypothesis?

The most common way of answering this is, if the p-value is low (less than the alpha), the Null should be rejected. If the p-value is high (greater than the alpha), then the null should not be rejected.

Summing up hypothesis testing

Hypothesis testing is a powerful statistical technique for confirming whether something is as you believe it is. You first state your basic or null hypothesis followed by your alternative one. You decide on the risk you are willing to take of being wrong. Collect your data, and use the appropriate statistical test based on your statistical question and type of data. Interpret your results, and draw a conclusion as to whether your null hypothesis was correct or not.

Join 65,000 Black Belts and Register For The Industry Leading ISIXSIGMA Newsletter Today

About the author.

Ken Feldman

Follow Me On:

Six Sigma Study Guide

Study notes and guides for Six Sigma certification tests

Basic Hypothesis Testing Process

Posted by Ted Hessing

Often used in science, mathematics, and other fields of knowledge, the Basic Hypothesis Testing Process provides a framework for identifying a question you would like to answer, determining the data you need in order to achieve significant results, choosing the correct test for your hypothesis, interpreting the results, and making a decision based on the data.

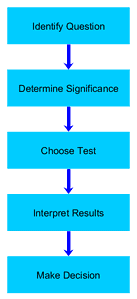
Identify Question

It’s vitally important to figure out which question you’re actually trying to answer. Once you have that, you can develop your null and alternative hypotheses. Generally speaking, you’re looking to create a simple question that asks whether factor x affects scenario  y , with an answer of ‘yes’ or ‘no’.

Examples of Hypothesis Questions

My friend has very pale blond hair. He tells me that his hair is fine because it’s blond. I disagree — I think that fine hair can be found in any hair color.

To figure this out once and for all, I could test his basic claim that blond hair is more likely to be fine than other hair colors.

A bad example of a question would be:

Is blond hair or other hair colors more likely to be fine?

Why? Because it doesn’t lend itself to a yes/no answer. It’s actually proposing three possible answers (‘blond’, ‘other’, ‘chance’), rather than offering a choice between ‘chance’ and ‘not chance’. Plus, it doesn’t actually define ‘fine’ hair in measurable terms.

A good example of a question would be:

Is hair classified as naturally ‘blond’ more likely to measure less than 60 microns in diameter?

Identify your Null and Alternative Hypothesis

Once I’ve framed the question in a simple yes/no format without ambiguities, developing the null and alternative hypotheses is actually pretty simple. The null hypothesis should state that chance is the only factor in seeming correlations between hair color and hair diameter:

There is no correlation between hair color and the diameter of a single hair.

The  alternative hypothesis should state that, as my friend claims, blond hair is more likely to be of small diameter:

Hair classified as naturally ‘blond’ is more likely to measure less than 60 microns in diameter.

Null Hypothesis ( H 0 )

The assumption that experimental results are due to chance alone is called Null Hypothesis.

First, a Null Hypothesis is what you would expect by chance alone.

Second, a Null Hypothesis assumes things to be equal.

Third, a Null Hypothesis is NOT your theory

• The hypothesis test has two tails (or rejection regions).
• The alternative hypothesis contains a “not equal to” sign.
• It can be rejected by the test statistic being significantly large or small.

Statement of zero or no change. If the original claim includes equality (<=, =, or >=), it is the null hypothesis. If the original claim does not include equality (<, not equal, >) then the null hypothesis is the complement of the original claim. The null hypothesis always includes the equal sign. The decision is based on the null hypothesis.

Alternative Hypothesis ( H 1 or H a )

This is your theory.

A statement that is true if the null hypothesis is false. The type of test (left, right, or two-tail) is based on the alternative hypothesis .

When the null hypothesis contains only an equal sign, the alternative hypothesis contains a “not equal to” sign.

Alternative Hypothesis for a Two-Tailed Test

H0: µ new = µ current   Ha: µ new is not = µ current

Examples of Hypothesis Statements

Ex. Are Cycle times / Error rates / Conversion rates statistically different based on different features (groups of people, processes followed, geography, level of training, age, etc)

Example: Has the cycle time of my transaction changed from year 1 to year 2?

H0 = Average of Year 1 = Average of Year 2 ; No change occurred; any change is due to chance alone Ha =  Average of Year 1 NOT = Average of Year 2.

Example # 2: Determine if a new machining process has reduced the diameter of a product

H0 = It did not reduce the diameter HA = It did reduce the diameter

Beware of Hypothesis Testing Errors

• Type 1 Error (Alpha)  – Happens when our significance level is too large
• Type 2 Error (Beta) – Happens when our significance level is too small

Type I error (alpha risk)

Rejecting the null hypothesis when it is true (saying false when true). Usually the more serious error.

Type 1 error involves the Significance level. For example, if alpha = 5%, then 5% of the time we will say there is a real difference between the null and alternate hypothesis (reject the null hypothesis) when there is no evidence of a difference.

Type II error (beta risk)

Failing to reject the null hypothesis when it is false (saying true when false).

Probability of committing a Type I error.

Probability of committing a Type II error.

Determine Significance

The next step is to figure out the significance applied to your test. This consists of two basic elements: sample size and confidence level.

When it comes to the sample size, the ideal is to gather data for the whole population on which you’re focusing. However, trying to gather data on a whole population (for example, the entire population of the United States) is cost-prohibitive. So you need a  sample of the population – one that is large enough to provide an acceptable cross-section of the population in terms of the hypotheses being tested.

You also need to decide on a  confidence level . This is how sure you need to be that the results you receive are actually statistically significant and that the conclusion based on them is correct. Once you’ve decided that, you can calculate the alpha level , which is simply (1 – confidence level). The standard confidence level used is 95%, or 0.95. Hence, the standard alpha level is 5%, or 0.05.

How certain do we need to be of the sampling ? Remember, you only use hypothesis testing when analyzing a sample of an entire population.

Choose Test

It’s important to choose the correct style of test to apply to your sample. This depends on the hypotheses you’re looking at and the kind of data that you’re using. Some basic questions that can help you to decide which test to use are:

• What level of measurement was used?
• How many different samples were used?
• What type of analysis do you need to do?

The questions that you need to ask could be far more complicated – see the National Center for Biotechnology’s in-depth article,  How to choose the right statistical test?

Interpret Results

Once you’ve run your data through the selected test, you’ll have your results. But that’s not the end of your work! The next step is to interpret those results. One of the key values supplied by any statistical test is the p-value , which gives you the probability that you will make an error in your conclusion depending on the results.

Test statistic

The Test Statistic is calculated from sample data. In order to test the null hypothesis, a test calculation is made from the sample. That calculated (test) value is then compared to a critical value. Depending on the comparison, decisions are made based on where the test statistic falls based on the critical value.

The NULL hypothesis is never accepted; we fail to reject it. We are always testing the NULL.

If the TEST STATISTIC falls in the rejection region (beyond critical value), then we REJECT THE NULL

Confidence level (95%) + Significance level (5%) = 100 % Due to chance alone, 95% of the time the test statistic will fall in the “Fail to reject” region, and 5% of the time, due to chance alone, the test statistic will fall in the “Critical region or Rejection Region”

P value: The probability of the sample being studied could have been drawn from the population due to chance

If P is low, Null must Go

A p-value less than the alpha level decided upon in the Decide Significance step means that you can assume that your results are statistically significant. The null hypothesis can be rejected, and the alternative hypothesis can be supported.

A p-value greater than the alpha level means that you cannot  assume that your results are statistically significant, and hence cannot reject the null hypothesis.

• The P value is integral in using a hypothesis test to make a decision. It reflects the possibility of falsely rejecting the null hypothesis when it really is true.
• If the P value is less than or equal to the agreed-upon significance level (alpha), then you reject the null and can support the alternate hypothesis.
• If the P value is greater, then you cannot reject the null hypothesis. (in stats terms, you have to fail to reject the null) And thus you cannot support the alternate.

This video walk-through of an independent sample t-test provides a simple example of interpreting test results:

Make Decision

The final step is to make a decision from your results and draw up your conclusion. There are two basic decisions that you can make when you’ve interpreted the results:

• Reject the null hypothesis and support the alternative hypothesis.
• Fail to reject the null hypothesis.

Once you’ve made the decision, you need to construct a conclusion. This should clearly communicate your original hypothesis, the sample on which it was tested, the decision you made, and any additional information that you think is important to convey.

This video provides some good step-by-step instructions on how to construct a conclusion based on your decision:

Six Sigma Black Belt Certification for Hypothesis Questions:

Question: Which of the following terms is used to describe the risk of a type I error in a hypothesis test?

(Taken from ASQ sample Black Belt exam .)

(A) Power (B) Confidence level (C) Level of significance (D) Beta risk

Unlock Additional Members-only Content!

Thank you for being a member.

C: Level of Significance. A type 1 error involves the Significance level. For example, if alpha = 5%, then 5% of the time we will say there is a real difference between the null and alternate hypothesis (reject the null hypothesis) when there is no evidence of a difference. The lower the alpha, the lower our chance of making a type 1 error.

I originally created SixSigmaStudyGuide.com to help me prepare for my own Black belt exams. Overtime I've grown the site to help tens of thousands of Six Sigma belt candidates prepare for their Green Belt & Black Belt exams. Go here to learn how to pass your Six Sigma exam the 1st time through!

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Determining Sample Size

Determining the right sample size is a crucial aspect of hypothesis testing in Lean Six Sigma projects, particularly when dealing with normal data. The sample size can significantly influence the power of a test, which is the probability that the test will correctly reject a false null hypothesis. A well-calculated sample size ensures that the study is both efficient and reliable, minimizing the risk of Type I (false positive) and Type II (false negative) errors.

Understanding Power and Sample Size

Before diving into the calculation of sample size, it's essential to understand the concept of power in hypothesis testing. Power is the likelihood that a test will detect a true effect when one exists. It's affected by several factors, including the sample size, the significance level (alpha), the effect size, and the variability of the data. A higher power means a higher probability of detecting a true effect, making it a critical consideration in study design.

Factors Influencing Sample Size

Several key factors need to be considered when determining the sample size for a hypothesis test:

Significance Level (Alpha):  The probability of rejecting the null hypothesis when it is true. A common alpha value is 0.05, but this can be adjusted based on the context of the study.

Power (1 - Beta):  The desired probability of correctly rejecting the null hypothesis. A typical power value is 0.80 or 80%, meaning there's an 80% chance of detecting an effect if there is one.

Effect Size:  The magnitude of the difference or effect that is considered practically significant for the study. This could be a difference between means, a correlation coefficient, or another measure relevant to the study.

Variability:  The variability in the data, often measured as the standard deviation. More variability requires a larger sample size to detect the same effect size.

Calculating Sample Size

The calculation of sample size is based on the aforementioned factors and often employs statistical software or sample size calculators. However, the basic principle revolves around ensuring that the test has enough power to detect the effect size of interest, given the variability in the data and the chosen significance level.

A simplified formula for calculating sample size for comparing two means (assuming equal variance and sample size in both groups) is:

n  is the sample size per group,

Zα /2​  is the Z-score associated with the desired alpha level (e.g., 1.96 for alpha = 0.05),

Zβ ​  is the Z-score associated with the desired power (e.g., 0.84 for power = 0.80),

δ  is the effect size (difference between means),

σ  is the standard deviation of the data.

Practical Considerations

When determining sample size, practical considerations must also be taken into account, including the available resources, time constraints, and the potential for data loss or non-response. It's often recommended to conduct a sensitivity analysis, adjusting the parameters to see how changes affect the required sample size. This can help in understanding the trade-offs involved and in making informed decisions about the study design.

Determining the appropriate sample size is a fundamental step in the design of a Lean Six Sigma project involving hypothesis testing with normal data. It requires careful consideration of the study's goals, the expected variability in the data, and the desired levels of significance and power. By adequately addressing these factors, researchers can ensure their study is capable of detecting meaningful effects, thereby contributing valuable insights to the process improvement efforts.

Please be aware that within the Lean Six Sigma Black Belt certification, you will not encounter exam questions that simultaneously address both Power and Sample Size. The focus will strictly be on questions related to Sample Size. Therefore, we provide an example solely concerning Sample Size for your consideration.

The objective is to reduce the cycle time of a product assembly line. Initial observations suggest that the process variability is high, and we aim to establish a baseline cycle time before implementing any changes. The project requires us to determine the sample size needed to estimate the average cycle time with a specific level of confidence and margin of error.

Step 1: Define the Parameters

Confidence Level (CL):  95% - This is a common confidence level used in Six Sigma projects, indicating that we are 95% confident that the true mean lies within our calculated interval.

Margin of Error (E):  0.5 minutes - This is the maximum acceptable difference between the sample mean and the population mean. Smaller margins of error require larger sample sizes.

Standard Deviation (σ):  2 minutes - Estimated based on pilot studies or historical data. If not available, collecting preliminary data from a small sample is necessary.

Step 2: Use the Sample Size Formula

For estimating a mean, the sample size formula is:

n  is the sample size

Z  is the Z-score corresponding to the desired confidence level (1.96 for 95% confidence level)

σ  is the estimated standard deviation

E  is the margin of error

Step 3: Calculate the Sample Size

Z =1.96  for 95% confidence

σ =2  minutes

E =0.5  minutes

Step 4: Round Up

The sample size must be a whole number, so we round up to the nearest whole number:

Conclusion:

To estimate the average cycle time of the product assembly line with a 95% confidence level and a margin of error of 0.5 minutes, we need a sample size of 62 observations. This means we must measure the cycle time of the assembly process 62 times under similar conditions to achieve the desired precision in our estimate.

Curent Location

LSS_BoK_3.4 - Hypothesis Testing with Normal Data

G) Power and Sample Size in Hypothesis Testing

Sub Section:

Previous article:

Next article:

• Dr. Juran’s History
• Dr. Joseph A. DeFeo
• Need a Speaker?
• The Juran Excellence Model
• The Juran Roadmap
• Quality by Design (QbD) & DFSS
• Conintuous Improvement
• Quality Control & Assurance
• LSS Certification
• Certification Project Reviews
• Coaching Support
• Training & Consulting
• IMPRO Online Learning
• IMPRO Website
• Organizational Assessments
• Free Lean Six Sigma White Belt
• Lean Six Sigma Yellow Belt
• Lean Six Sigma Green Belt
• Upgrade to LSS Black Belt
• Lean Six Sigma Black Belt
• Lean Six Sigma MBB
• Lean Expert Program
• Root Cause Analysis
• Quality Auditor
• Certified Quality Director
• Quality By Design Green Belt
• Introduction to Statistics
• Hypothesis Testing
• Design of Experiments
• Measurement System Analysis
• Quality Leader’s Certification
• Launching Effective Teams
• Facilitation Skills for Project Leaders
• Training the Adult Learner
• Champion Training
• Making Quality Happen
• COQ & COPQ
• Food Processing
• Healthcare and Hospitals
• Manufacturing
• Pharmaceutical
• Higher Education
• Project Case Study Examples
• Juran Quality Handbook
• Hot Topic Webinars
• Published Papers
• Quality Minute Videos

How to Write a Six Sigma Problem Statement

Juran December 19, 2019 Blog Leave a Comment

A Six Sigma problem statement recognizes that there is a gap between the reality of a situation versus what should be the case and initiates the process of correcting the anomaly.

It focuses on one of four main areas: an issue or area that gives cause for concern, a situation that needs to be improved, a snag that needs to be eliminated, or a worrying question – theoretical or actual – that indicates a need for balanced scrutiny.

The problem statement is a key element of the “Define” stage of the DMAIC (Define, Measure, Analyze, Improve, Control) process. Quite simply, it defines the issue that needs to be addressed.

What should a problem statement include?

A Six Sigma problem statement should be concise, specific, and fact-based. General and/or long-winded statements won’t focus on the key issue, and anything not backed up by verifiable data is opinion, prone to bias, and able to misdirect an investigation.

Problem statements should focus on a single issue. Start with the precise location where the problem is happening and the specific process involved. Supporting facts may include how often, how many, how long, plus recorded data that helps illustrate the issue. In addition, include information that shows the financial impact the issue is having on the organization.

Acknowledging the challenges

One of the hardest things to do is to focus solely on the issue and not be distracted by side issues. It can be tempting to assign blame, for example, but that suggests you are no longer open-minded when it comes to seeking out the root cause.

You might feel that, having pulled together all the information, you have a sufficiently clear understanding of the problem to know what needs to be done to fix it. However, you must resist the temptation to suggest a solution at this stage, as an investigation is likely to uncover additional information.

An effective problem statement defines the issue and conveys a sense of urgency. It sets out only the facts; the ensuing investigation identifies the root cause, which will lead to an appropriate solution.

The Six Sigma Project Charter

A problem statement is the first of the six elements comprising a broader Six Sigma Project Charter. The six are:

The problem statement, which defines an issue and how it is affecting the organization.

The goal statement, which should be in line with the problem you seek to solve, and which should be SMART – specific, measurable, attainable, relevant and time-bound.

The business case, which sets out why a project is important to an organization and deserves its support.

The scope statement, which defines the limits of the project and shows both what should be included and what should be excluded.

The project milestones, outlining the key activities that need to be completed and the projected dates of completion.

A list of the team members that will be working on the project, which will depend on the problem that needs solving and project scope.

Setting the project statement in this context gives the bigger overall picture and aids understanding. It helps avoid some of the common pitfalls described above.

For more information on DMAIC methodology or Lean Six Sigma , please browse our Knowledge Base . Alternatively, get in touch to find out more about our LSS training courses or visit our dedicated program pages.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Recommended Reading

Juran daily kata, quality 4.0: revolutionizing quality in manufacturing through digital transformation, the art of agile and scrum.

Lean Six Sigma Training Certification

• Facebook Instagram Twitter LinkedIn YouTube
• (877) 497-4462

Hypothesis statement

August 5th, 2013

A complete description of the suspected cause(s) of a process problem.

SixSigma.us offers both Live Virtual classes as well as Online Self-Paced training. Most option includes access to the same great Master Black Belt instructors that teach our World Class in-person sessions. Sign-up today!

Virtual Classroom Training Programs Self-Paced Online Training Programs

SixSigma.us Accreditation & Affiliations

Monthly Management Tips

• Be the first one to receive the latest updates and information from 6Sigma
• Get curated resources from industry-experts
• Gain an edge with complete guides and other exclusive materials
• Become a part of one of the largest Six Sigma community
• Unlock your path to become a Six Sigma professional

" * " indicates required fields