homework 2 adding and subtracting rational expressions

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.3: Add and Subtract Rational Expressions

• Last updated
• Save as PDF
• Page ID 114203

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Add and subtract rational expressions with a common denominator
• Add and subtract rational expressions whose denominators are opposites
• Find the least common denominator of rational expressions
• Add and subtract rational expressions with unlike denominators

Add and subtract rational functions

Be prepared 7.4.

Before you get started, take this readiness quiz.

Add: 7 10 + 8 15 . 7 10 + 8 15 . If you missed this problem, review Example 1.29.

Be Prepared 7.5

Subtract: 3 x 4 − 8 9 . 3 x 4 − 8 9 . If you missed this problem, review Example 1.28.

Be Prepared 7.6

Subtract: 6 ( 2 x + 1 ) − 4 ( x − 5 ) . 6 ( 2 x + 1 ) − 4 ( x − 5 ) . If you missed this problem, review Example 1.56.

Add and Subtract Rational Expressions with a Common Denominator

What is the first step you take when you add numerical fractions? You check if they have a common denominator. If they do, you add the numerators and place the sum over the common denominator. If they do not have a common denominator, you find one before you add.

It is the same with rational expressions. To add rational expressions, they must have a common denominator. When the denominators are the same, you add the numerators and place the sum over the common denominator.

Rational Expression Addition and Subtraction

If p , q , and r are polynomials where r ≠ 0 , r ≠ 0 , then

p r + q r = p + q r and p r − q r = p − q r p r + q r = p + q r and p r − q r = p − q r

To add or subtract rational expressions with a common denominator, add or subtract the numerators and place the result over the common denominator.

We always simplify rational expressions. Be sure to factor, if possible, after you subtract the numerators so you can identify any common factors.

Remember, too, we do not allow values that would make the denominator zero. What value of x should be excluded in the next example?

Example 7.13

Add: 11 x + 28 x + 4 + x 2 x + 4 . 11 x + 28 x + 4 + x 2 x + 4 .

Since the denominator is x + 4 , x + 4 , we must exclude the value x = −4 . x = −4 .

The expression simplifies to x + 7 x + 7 but the original expression had a denominator of x + 4 x + 4 so x ≠ − 4 . x ≠ − 4 .

Try It 7.25

Simplify: 9 x + 14 x + 7 + x 2 x + 7 . 9 x + 14 x + 7 + x 2 x + 7 .

Try It 7.26

Simplify: x 2 + 8 x x + 5 + 15 x + 5 . x 2 + 8 x x + 5 + 15 x + 5 .

To subtract rational expressions, they must also have a common denominator. When the denominators are the same, you subtract the numerators and place the difference over the common denominator. Be careful of the signs when you subtract a binomial or trinomial.

Example 7.14

Subtract: 5 x 2 − 7 x + 3 x 2 − 3 x - 18 − 4 x 2 + x − 9 x 2 − 3 x - 18 . 5 x 2 − 7 x + 3 x 2 − 3 x - 18 − 4 x 2 + x − 9 x 2 − 3 x - 18 .

Try It 7.27

Subtract: 4 x 2 − 11 x + 8 x 2 − 3 x + 2 − 3 x 2 + x − 3 x 2 − 3 x + 2 . 4 x 2 − 11 x + 8 x 2 − 3 x + 2 − 3 x 2 + x − 3 x 2 − 3 x + 2 .

Try It 7.28

Subtract: 6 x 2 − x + 20 x 2 − 81 − 5 x 2 + 11 x − 7 x 2 − 81 . 6 x 2 − x + 20 x 2 − 81 − 5 x 2 + 11 x − 7 x 2 − 81 .

Add and Subtract Rational Expressions Whose Denominators are Opposites

When the denominators of two rational expressions are opposites, it is easy to get a common denominator. We just have to multiply one of the fractions by −1 −1 . −1 −1 .

Let’s see how this works.

Be careful with the signs as you work with the opposites when the fractions are being subtracted.

Example 7.15

Subtract: m 2 − 6 m m 2 − 1 − 3 m + 2 1 − m 2 . m 2 − 6 m m 2 − 1 − 3 m + 2 1 − m 2 .

Try It 7.29

Subtract: y 2 − 5 y y 2 − 4 − 6 y − 6 4 − y 2 . y 2 − 5 y y 2 − 4 − 6 y − 6 4 − y 2 .

Try It 7.30

Subtract: 2 n 2 + 8 n − 1 n 2 − 1 − n 2 − 7 n − 1 1 − n 2 . 2 n 2 + 8 n − 1 n 2 − 1 − n 2 − 7 n − 1 1 − n 2 .

Find the Least Common Denominator of Rational Expressions

When we add or subtract rational expressions with unlike denominators, we will need to get common denominators. If we review the procedure we used with numerical fractions, we will know what to do with rational expressions.

Let’s look at this example: 7 12 + 5 18 . 7 12 + 5 18 . Since the denominators are not the same, the first step was to find the least common denominator (LCD).

To find the LCD of the fractions, we factored 12 and 18 into primes, lining up any common primes in columns. Then we “brought down” one prime from each column. Finally, we multiplied the factors to find the LCD.

When we add numerical fractions, once we found the LCD, we rewrote each fraction as an equivalent fraction with the LCD by multiplying the numerator and denominator by the same number. We are now ready to add.

We do the same thing for rational expressions. However, we leave the LCD in factored form.

Find the least common denominator of rational expressions.

• Step 1. Factor each denominator completely.
• Step 2. List the factors of each denominator. Match factors vertically when possible.
• Step 3. Bring down the columns by including all factors, but do not include common factors twice.
• Step 4. Write the LCD as the product of the factors.

Remember, we always exclude values that would make the denominator zero. What values of x x should we exclude in this next example?

Example 7.16

ⓐ Find the LCD for the expressions 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 and ⓑ rewrite them as equivalent rational expressions with the lowest common denominator.

Try It 7.31

ⓐ Find the LCD for the expressions 2 x 2 − x − 12 , 1 x 2 − 16 2 x 2 − x − 12 , 1 x 2 − 16 ⓑ rewrite them as equivalent rational expressions with the lowest common denominator.

Try It 7.32

ⓐ Find the LCD for the expressions 3 x x 2 − 3 x – 10 , 5 x 2 + 3 x + 2 3 x x 2 − 3 x – 10 , 5 x 2 + 3 x + 2 ⓑ rewrite them as equivalent rational expressions with the lowest common denominator.

Add and Subtract Rational Expressions with Unlike Denominators

Now we have all the steps we need to add or subtract rational expressions with unlike denominators.

Example 7.17

How to add rational expressions with unlike denominators.

Add: 3 x − 3 + 2 x − 2 . 3 x − 3 + 2 x − 2 .

Try It 7.33

Add: 2 x − 2 + 5 x + 3 . 2 x − 2 + 5 x + 3 .

Try It 7.34

Add: 4 m + 3 + 3 m + 4 . 4 m + 3 + 3 m + 4 .

The steps used to add rational expressions are summarized here.

Add or subtract rational expressions.

• Yes – go to step 2.
• Find the LCD.
• Rewrite each rational expression as an equivalent rational expression with the LCD.
• Step 2. Add or subtract the rational expressions.
• Step 3. Simplify, if possible.

Avoid the temptation to simplify too soon. In the example above, we must leave the first rational expression as 3 x − 6 ( x − 3 ) ( x − 2 ) 3 x − 6 ( x − 3 ) ( x − 2 ) to be able to add it to 2 x − 6 ( x − 2 ) ( x − 3 ) . 2 x − 6 ( x − 2 ) ( x − 3 ) . Simplify only after you have combined the numerators.

Example 7.18

Add: 8 x 2 − 2 x − 3 + 3 x x 2 + 4 x + 3 . 8 x 2 − 2 x − 3 + 3 x x 2 + 4 x + 3 .

Try It 7.35

Add: 1 m 2 − m − 2 + 5 m m 2 + 3 m + 2 . 1 m 2 − m − 2 + 5 m m 2 + 3 m + 2 .

Try It 7.36

Add: 2 n n 2 − 3 n − 10 + 6 n 2 + 5 n + 6 . 2 n n 2 − 3 n − 10 + 6 n 2 + 5 n + 6 .

The process we use to subtract rational expressions with different denominators is the same as for addition. We just have to be very careful of the signs when subtracting the numerators.

Example 7.19

Subtract: 8 y y 2 − 16 − 4 y − 4 . 8 y y 2 − 16 − 4 y − 4 .

Try It 7.37

Subtract: 2 x x 2 − 4 − 1 x + 2 . 2 x x 2 − 4 − 1 x + 2 .

Try It 7.38

Subtract: 3 z + 3 − 6 z z 2 − 9 . 3 z + 3 − 6 z z 2 − 9 .

There are lots of negative signs in the next example. Be extra careful.

Example 7.20

Subtract: −3 n − 9 n 2 + n − 6 − n + 3 2 − n . −3 n − 9 n 2 + n − 6 − n + 3 2 − n .

Try It 7.39

Subtract : 3 x − 1 x 2 − 5 x − 6 − 2 6 − x . 3 x − 1 x 2 − 5 x − 6 − 2 6 − x .

Try It 7.40

Subtract: −2 y − 2 y 2 + 2 y − 8 − y − 1 2 − y . −2 y − 2 y 2 + 2 y − 8 − y − 1 2 − y .

Things can get very messy when both fractions must be multiplied by a binomial to get the common denominator.

Example 7.21

Subtract: 4 a 2 + 6 a + 5 − 3 a 2 + 7 a + 10 . 4 a 2 + 6 a + 5 − 3 a 2 + 7 a + 10 .

Try It 7.41

Subtract: 3 b 2 − 4 b − 5 − 2 b 2 − 6 b + 5 . 3 b 2 − 4 b − 5 − 2 b 2 − 6 b + 5 .

Try It 7.42

Subtract: 4 x 2 − 4 − 3 x 2 − x − 2 . 4 x 2 − 4 − 3 x 2 − x − 2 .

We follow the same steps as before to find the LCD when we have more than two rational expressions. In the next example, we will start by factoring all three denominators to find their LCD.

Example 7.22

Simplify: 2 u u − 1 + 1 u − 2 u − 1 u 2 − u . 2 u u − 1 + 1 u − 2 u − 1 u 2 − u .

Try It 7.43

Simplify: v v + 1 + 3 v − 1 − 6 v 2 − 1 . v v + 1 + 3 v − 1 − 6 v 2 − 1 .

Try It 7.44

Simplify: 3 w w + 2 + 2 w + 7 − 17 w + 4 w 2 + 9 w + 14 . 3 w w + 2 + 2 w + 7 − 17 w + 4 w 2 + 9 w + 14 .

To add or subtract rational functions, we use the same techniques we used to add or subtract polynomial functions.

Example 7.23

Find R ( x ) = f ( x ) − g ( x ) R ( x ) = f ( x ) − g ( x ) where f ( x ) = x + 5 x − 2 f ( x ) = x + 5 x − 2 and g ( x ) = 5 x + 18 x 2 − 4 . g ( x ) = 5 x + 18 x 2 − 4 .

Try It 7.45

Find R ( x ) = f ( x ) − g ( x ) R ( x ) = f ( x ) − g ( x ) where f ( x ) = x + 1 x + 3 f ( x ) = x + 1 x + 3 and g ( x ) = x + 17 x 2 − x − 12 . g ( x ) = x + 17 x 2 − x − 12 .

Try It 7.46

Find R ( x ) = f ( x ) + g ( x ) R ( x ) = f ( x ) + g ( x ) where f ( x ) = x − 4 x + 3 f ( x ) = x − 4 x + 3 and g ( x ) = 4 x + 6 x 2 − 9 . g ( x ) = 4 x + 6 x 2 − 9 .

Access this online resource for additional instruction and practice with adding and subtracting rational expressions.

• Add and Subtract Rational Expressions- Unlike Denominators

Section 7.2 Exercises

Practice makes perfect.

In the following exercises, add.

2 15 + 7 15 2 15 + 7 15

7 24 + 11 24 7 24 + 11 24

3 c 4 c − 5 + 5 4 c − 5 3 c 4 c − 5 + 5 4 c − 5

7 m 2 m + n + 4 2 m + n 7 m 2 m + n + 4 2 m + n

2 r 2 2 r − 1 + 15 r − 8 2 r − 1 2 r 2 2 r − 1 + 15 r − 8 2 r − 1

3 s 2 3 s − 2 + 13 s − 10 3 s − 2 3 s 2 3 s − 2 + 13 s − 10 3 s − 2

2 w 2 w 2 − 16 + 8 w w 2 − 16 2 w 2 w 2 − 16 + 8 w w 2 − 16

7 x 2 x 2 − 9 + 21 x x 2 − 9 7 x 2 x 2 − 9 + 21 x x 2 − 9

In the following exercises, subtract.

9 a 2 3 a − 7 − 49 3 a − 7 9 a 2 3 a − 7 − 49 3 a − 7

25 b 2 5 b − 6 − 36 5 b − 6 25 b 2 5 b − 6 − 36 5 b − 6

3 m 2 6 m − 30 − 21 m − 30 6 m − 30 3 m 2 6 m − 30 − 21 m − 30 6 m − 30

2 n 2 4 n − 32 − 18 n − 16 4 n − 32 2 n 2 4 n − 32 − 18 n − 16 4 n − 32

6 p 2 + 3 p + 4 p 2 + 4 p − 5 − 5 p 2 + p + 7 p 2 + 4 p − 5 6 p 2 + 3 p + 4 p 2 + 4 p − 5 − 5 p 2 + p + 7 p 2 + 4 p − 5

5 q 2 + 3 q − 9 q 2 + 6 q + 8 − 4 q 2 + 9 q + 7 q 2 + 6 q + 8 5 q 2 + 3 q − 9 q 2 + 6 q + 8 − 4 q 2 + 9 q + 7 q 2 + 6 q + 8

5 r 2 + 7 r − 33 r 2 − 49 − 4 r 2 + 5 r + 30 r 2 − 49 5 r 2 + 7 r − 33 r 2 − 49 − 4 r 2 + 5 r + 30 r 2 − 49

7 t 2 − t − 4 t 2 − 25 − 6 t 2 + 12 t − 44 t 2 − 25 7 t 2 − t − 4 t 2 − 25 − 6 t 2 + 12 t − 44 t 2 − 25

Add and Subtract Rational Expressions whose Denominators are Opposites

In the following exercises, add or subtract.

10 v 2 v − 1 + 2 v + 4 1 − 2 v 10 v 2 v − 1 + 2 v + 4 1 − 2 v

20 w 5 w − 2 + 5 w + 6 2 − 5 w 20 w 5 w − 2 + 5 w + 6 2 − 5 w

10 x 2 + 16 x − 7 8 x − 3 + 2 x 2 + 3 x − 1 3 − 8 x 10 x 2 + 16 x − 7 8 x − 3 + 2 x 2 + 3 x − 1 3 − 8 x

6 y 2 + 2 y − 11 3 y − 7 + 3 y 2 − 3 y + 17 7 − 3 y 6 y 2 + 2 y − 11 3 y − 7 + 3 y 2 − 3 y + 17 7 − 3 y

z 2 + 6 z z 2 − 25 − 3 z + 20 25 − z 2 z 2 + 6 z z 2 − 25 − 3 z + 20 25 − z 2

a 2 + 3 a a 2 − 9 − 3 a − 27 9 − a 2 a 2 + 3 a a 2 − 9 − 3 a − 27 9 − a 2

2 b 2 + 30 b − 13 b 2 − 49 − 2 b 2 − 5 b − 8 49 − b 2 2 b 2 + 30 b − 13 b 2 − 49 − 2 b 2 − 5 b − 8 49 − b 2

c 2 + 5 c − 10 c 2 − 16 − c 2 − 8 c − 10 16 − c 2 c 2 + 5 c − 10 c 2 − 16 − c 2 − 8 c − 10 16 − c 2

In the following exercises, ⓐ find the LCD for the given rational expressions ⓑ rewrite them as equivalent rational expressions with the lowest common denominator.

5 x 2 − 2 x − 8 , 2 x x 2 − x − 12 5 x 2 − 2 x − 8 , 2 x x 2 − x − 12

8 y 2 + 12 y + 35 , 3 y y 2 + y − 42 8 y 2 + 12 y + 35 , 3 y y 2 + y − 42

9 z 2 + 2 z − 8 , 4 z z 2 − 4 9 z 2 + 2 z − 8 , 4 z z 2 − 4

6 a 2 + 14 a + 45 , 5 a a 2 − 81 6 a 2 + 14 a + 45 , 5 a a 2 − 81

4 b 2 + 6 b + 9 , 2 b b 2 − 2 b − 15 4 b 2 + 6 b + 9 , 2 b b 2 − 2 b − 15

5 c 2 − 4 c + 4 , 3 c c 2 − 7 c + 10 5 c 2 − 4 c + 4 , 3 c c 2 − 7 c + 10

2 3 d 2 + 14 d − 5 , 5 d 3 d 2 − 19 d + 6 2 3 d 2 + 14 d − 5 , 5 d 3 d 2 − 19 d + 6

3 5 m 2 − 3 m − 2 , 6 m 5 m 2 + 17 m + 6 3 5 m 2 − 3 m − 2 , 6 m 5 m 2 + 17 m + 6

In the following exercises, perform the indicated operations.

7 10 x 2 y + 4 15 x y 2 7 10 x 2 y + 4 15 x y 2

1 12 a 3 b 2 + 5 9 a 2 b 3 1 12 a 3 b 2 + 5 9 a 2 b 3

3 r + 4 + 2 r − 5 3 r + 4 + 2 r − 5

4 s − 7 + 5 s + 3 4 s − 7 + 5 s + 3

5 3 w − 2 + 2 w + 1 5 3 w − 2 + 2 w + 1

4 2 x + 5 + 2 x − 1 4 2 x + 5 + 2 x − 1

2 y y + 3 + 3 y − 1 2 y y + 3 + 3 y − 1

3 z z − 2 + 1 z + 5 3 z z − 2 + 1 z + 5

5 b a 2 b − 2 a 2 + 2 b b 2 − 4 5 b a 2 b − 2 a 2 + 2 b b 2 − 4

4 c d + 3 c + 1 d 2 − 9 4 c d + 3 c + 1 d 2 − 9

−3 m 3 m − 3 + 5 m m 2 + 3 m − 4 −3 m 3 m − 3 + 5 m m 2 + 3 m − 4

8 4 n + 4 + 6 n 2 − n − 2 8 4 n + 4 + 6 n 2 − n − 2

3 r r 2 + 7 r + 6 + 9 r 2 + 4 r + 3 3 r r 2 + 7 r + 6 + 9 r 2 + 4 r + 3

2 s s 2 + 2 s − 8 + 4 s 2 + 3 s − 10 2 s s 2 + 2 s − 8 + 4 s 2 + 3 s − 10

t t − 6 − t − 2 t + 6 t t − 6 − t − 2 t + 6

x − 3 x + 6 − x x + 3 x − 3 x + 6 − x x + 3

5 a a + 3 − a + 2 a + 6 5 a a + 3 − a + 2 a + 6

3 b b − 2 − b − 6 b − 8 3 b b − 2 − b − 6 b − 8

6 m + 6 − 12 m m 2 − 36 6 m + 6 − 12 m m 2 − 36

4 n + 4 − 8 n n 2 − 16 4 n + 4 − 8 n n 2 − 16

−9 p − 17 p 2 − 4 p − 21 − p + 1 7 − p −9 p − 17 p 2 − 4 p − 21 − p + 1 7 − p

− 13 q − 8 q 2 + 2 q − 24 − q + 2 4 − q − 13 q − 8 q 2 + 2 q − 24 − q + 2 4 − q

−2 r − 16 r 2 + 6 r − 16 − 5 2 − r −2 r − 16 r 2 + 6 r − 16 − 5 2 − r

2 t − 30 t 2 + 6 t − 27 − 2 3 − t 2 t − 30 t 2 + 6 t − 27 − 2 3 − t

2 x + 7 10 x − 1 + 3 2 x + 7 10 x − 1 + 3

8 y − 4 5 y + 2 − 6 8 y − 4 5 y + 2 − 6

3 x 2 − 3 x − 4 − 2 x 2 − 5 x + 4 3 x 2 − 3 x − 4 − 2 x 2 − 5 x + 4

4 x 2 − 6 x + 5 − 3 x 2 − 7 x + 10 4 x 2 − 6 x + 5 − 3 x 2 − 7 x + 10

5 x 2 + 8 x − 9 − 4 x 2 + 10 x + 9 5 x 2 + 8 x − 9 − 4 x 2 + 10 x + 9

3 2 x 2 + 5 x + 2 − 1 2 x 2 + 3 x + 1 3 2 x 2 + 5 x + 2 − 1 2 x 2 + 3 x + 1

5 a a − 2 + 9 a − 2 a + 18 a 2 − 2 a 5 a a − 2 + 9 a − 2 a + 18 a 2 − 2 a

2 b b − 5 + 3 2 b − 2 b − 15 2 b 2 − 10 b 2 b b − 5 + 3 2 b − 2 b − 15 2 b 2 − 10 b

c c + 2 + 5 c − 2 − 10 c c 2 − 4 c c + 2 + 5 c − 2 − 10 c c 2 − 4

6 d d − 5 + 1 d + 4 − 7 d − 5 d 2 − d − 20 6 d d − 5 + 1 d + 4 − 7 d − 5 d 2 − d − 20

3 d d + 2 + 4 d − d + 8 d 2 + 2 d 3 d d + 2 + 4 d − d + 8 d 2 + 2 d

2 q q + 5 + 3 q − 3 − 13 q + 15 q 2 + 2 q − 15 2 q q + 5 + 3 q − 3 − 13 q + 15 q 2 + 2 q − 15

Add and Subtract Rational Functions

In the following exercises, find ⓐ R ( x ) = f ( x ) + g ( x ) R ( x ) = f ( x ) + g ( x ) ⓑ R ( x ) = f ( x ) − g ( x ) . R ( x ) = f ( x ) − g ( x ) .

f ( x ) = −5 x − 5 x 2 + x − 6 f ( x ) = −5 x − 5 x 2 + x − 6 and g ( x ) = x + 1 2 − x g ( x ) = x + 1 2 − x

f ( x ) = −4 x − 24 x 2 + x − 30 f ( x ) = −4 x − 24 x 2 + x − 30 and g ( x ) = x + 7 5 − x g ( x ) = x + 7 5 − x

f ( x ) = 6 x x 2 − 64 f ( x ) = 6 x x 2 − 64 and g ( x ) = 3 x − 8 g ( x ) = 3 x − 8

f ( x ) = 5 x + 7 f ( x ) = 5 x + 7 and g ( x ) = 10 x x 2 − 49 g ( x ) = 10 x x 2 − 49

Writing Exercises

Donald thinks that 3 x + 4 x 3 x + 4 x is 7 2 x . 7 2 x . Is Donald correct? Explain.

Explain how you find the Least Common Denominator of x 2 + 5 x + 4 x 2 + 5 x + 4 and x 2 − 16 . x 2 − 16 .

Felipe thinks 1 x + 1 y 1 x + 1 y is 2 x + y . 2 x + y . ⓐ Choose numerical values for x and y and evaluate 1 x + 1 y . 1 x + 1 y . ⓑ Evaluate 2 x + y 2 x + y for the same values of x and y you used in part ⓐ . ⓒ Explain why Felipe is wrong. ⓓ Find the correct expression for 1 x + 1 y . 1 x + 1 y .

Simplify the expression 4 n 2 + 6 n + 9 − 1 n 2 − 9 4 n 2 + 6 n + 9 − 1 n 2 − 9 and explain all your steps.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Rational Expressions

Adding and Subtracting Rational Expressions

Rational expressions with the same denominator.

To add/subtract rational expressions with the same denominator

1. Add/subtract the numerators. Write this sum/difference as the numerator over the common denominator.

2. Reduce to lowest terms.

Simplify the following:

$\frac{{4x}}{{5y}} + \frac{{6x}}{{5y}}$

These fractions already have a common denominator

1 : Write this sum as the numerator over the common denominator:

$\frac{{4x}}{{5y}} + \frac{{6x}}{{5y}} = \frac{{4x + 6x}}{{5y}}$

2 : Reduce to lowest terms:

$\frac{{4x}}{{5y}} + \frac{{6x}}{{5y}} = \frac{{4x + 6x}}{{5y}} = \frac{{10x}}{{5y}} = \frac{{2x}}{y}$

$\frac{{4x - 1}}{{x + 4}} - \frac{{2x - 9}}{{x + 4}}$

Again, these already have a common denominator

$\frac{{4x - 1}}{{x + 4}} - \frac{{2x - 9}}{{x + 4}} = \frac{{(4x - 1) - (2x - 9)}}{{x + 4}}$

$$\frac{{4x - 1}}{{x + 4}} - \frac{{2x - 9}}{{x + 4}} = \frac{{(4x - 1) - (2x - 9)}}{{x + 4}} = $$ $$ = \frac{{4x - 1 - 2x + 9}}{{x + 4}} = $$ $$ = \frac{{2x + 8}}{{x + 4}} = $$ $$ = \frac{{2\cancel{{(x + 4)}}}}{{\cancel{{x + 4}}}} = 2$$

Exercise 1: Simplify the following expression

Adding or Subtracting Rational Expressions with Different Denominators

1. Factor each denominator completely.

2. Build the LCD of the denominators.

3. Rewrite each rational expression with the LCD as the denominator.

4. Add/subtract the numerators.

$\frac{{5x - 1}}{{{x^2} - 3x + 2}} + \frac{3}{{2x - 4}}$

Solution 3:

1 : Factor each denominator completely.

$\frac{{5x - 1}}{{{x^2} - 3x + 2}} + \frac{2}{{2x - 4}} = \frac{{5x - 1}}{{(x - 1)(x - 2)}} + \frac{3}{{2(x - 2)}}$

2 : Build the LCD of the denominators.

$LCD = 2(x - 1)(x - 2)$

3 : Rewrite each rational expression with the LCD as the denominator.

$$\frac{{5x - 1}}{{{x^2} - 3x + 2}} + \frac{3}{{2x - 4}} = \frac{{5x - 1}}{{(x - 1)(x - 2)}} + \frac{3}{{2(x - 2)}} = $$ $$ = \frac{{2(5x - 1)}}{{2(x - 1)(x - 2)}} + \frac{{3(x - 1)}}{{2(x - 1)(x - 2)}}$$

4 : Add the numerators.

$$\frac{{5x - 1}}{{{x^2} - 3x + 2}} + \frac{3}{{2x - 4}} = \frac{{5x - 1}}{{(x - 1)(x - 2)}} + \frac{3}{{2(x - 2)}} = $$ $$ = \frac{{2(5x - 1)}}{{2(x - 1)(x - 2)}} + \frac{{3(x - 1)}}{{2(x - 1)(x - 2)}} = $$ $$ = \frac{{2(5x - 1) + 3(x - 1)}}{{2(x - 1)(x - 2)}} = $$ $$ = \frac{{13x - 5}}{{2(x - 1)(x - 2)}}$$

$\frac{{5x + 1}}{{{x^2} - 2x - 3}} - \frac{{5x - 3}}{{{x^2} - x - 6}}$

Solution 4:

$\frac{{5x + 1}}{{{x^2} - 2x - 3}} - \frac{{5x - 3}}{{{x^2} - x - 6}} = \frac{{5x + 1}}{{(x - 3)(x + 1)}} - \frac{{5x - 3}}{{(x - 3)(x + 2)}}$

$LCD = (x - 3)(x + 1)(x + 2)$

$$\frac{{5x + 1}}{{{x^2} - 2x - 3}} - \frac{{5x - 3}}{{{x^2} - x - 6}} = \frac{{5x + 1}}{{(x - 3)(x + 1)}} - \frac{{5x - 3}}{{(x - 3)(x + 2)}} = $$ $$ = \frac{{(5x + 1)(x + 2)}}{{(x - 3)(x + 1)(x + 2)}} - \frac{{(5x - 3)(x + 1)}}{{(x - 3)(x + 1)(x + 2)}}$$

4 : Subtract the numerators.

$$\frac{{5x + 1}}{{{x^2} - 2x - 3}} - \frac{{5x - 3}}{{{x^2} - x - 6}} = \frac{{5x + 1}}{{(x - 3)(x + 1)}} - \frac{{5x - 3}}{{(x - 3)(x + 2)}} = $$ $$ = \frac{{(5x + 1)(x + 2)}}{{(x - 3)(x + 1)(x + 2)}} - \frac{{(5x - 3)(x + 1)}}{{(x - 3)(x + 1)(x + 2)}} = $$ $$ = \frac{{(5x + 1)(x + 2) - (5x - 3)(x + 1)}}{{(x - 3)(x + 1)(x + 2)}} = $$ $$ = \frac{{(5{x^2} + 10x + x + 2) - (5{x^2} + 5x - 3x - 3)}}{{(x - 3)(x + 1)(x + 2)}} = $$ $$ = \frac{{5{x^2} + 10x + x + 2 - 5{x^2} - 5x + 3x + 3)}}{{(x - 3)(x + 1)(x + 2)}} = $$ $$ = \frac{{9x + 5}}{{(x - 3)(x + 1)(x + 2)}}$$

Exercise 2: Simplify the following expression

• Roots and Radicals Simplify Expression Adding and Subtracting Multiplying and Dividing
• Complex Numbers Arithmetic Polar representation
• Polynomials Multiplying Polynomials Division of Polynomials Zeros of Polynomials
• Rational Expressions Simplifying Multiplying and Dividing Adding and Subtracting
• Solving Equations Linear Equations Absolute Value Equations Quadratic Equation Equations with Radicals
• Systems of Equations Substitution Method Elimination Method Row Reduction Cramers Rule Inverse Matrix Method
• Exponential Functions Introduction Exponential Equations Logarithmic Functions
• Trigonometry Trigonometric Formulas Trigonometric Equations Law of Cosines
• Progressions Arithmetic Progressions Geometric Progressions
• Differentiation Common formulas Product and Quotient Rule Chain Rule
• Limits Properties of Limits Rational Function Irrational Functions Trigonometric Functions L'Hospital's Rule
• Integrals Integration Formulas Exercises
• Integral techniques Substitution Integration by Parts Integrals with Trig. Functions Trigonometric Substitutions
• Integral Applications Area Volume Arc Length

Analytic geometry

• Analytic Geometry 2D Basic Concepts Lines Parallel and Perpendicular Lines Polar Coordinates
• Conic Sections Circle Ellipse Hyperbola
• Analytic Geometry 3D Line in 3D Planes

Linear Algebra

• Matrices Definitions Addition and Multiplication Gauss-Jordan elimination
• Determinants Introduction to Determinants Applications of Determinants
• Vectors Basic Operations Dot Product Cross Product

Random Quote

Every good mathematician is at least half a philosopher, and every good philosopher is at least half a mathematician.

Friedrich Ludwig Gottlob Frege

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 4.

• Intro to adding & subtracting rational expressions
• Adding & subtracting rational expressions: like denominators
• Intro to adding rational expressions with unlike denominators
• Adding rational expression: unlike denominators
• Subtracting rational expressions: unlike denominators
• Add & subtract rational expressions (basic)

Adding & subtracting rational expressions

• Least common multiple of polynomials
• Subtracting rational expressions: factored denominators
• Subtracting rational expressions
• Add & subtract rational expressions
• Rational functions: FAQ

What we need to know before this lesson

• Intro to rational expressions

What you will learn in this lesson

Warm-up: 3 x − 2 − 2 x + 1 ‍  , check your understanding, least common denominators, numerical fractions.

• 4 ‍   and 6 ‍   share a common factor of 2 ‍   , so the LCM ‍   of 4 ‍   and 6 ‍   is 12 ‍   , not 4 ⋅ 6 = 24 ‍  
• 6 ‍   and 15 ‍   share a common factor of 3 ‍   , so the LCM ‍   of 6 ‍   and 15 ‍   is 30 ‍   , not 6 ⋅ 15 = 90 ‍  

Variable expressions

Why use the least common denominator, want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Adding and Subtracting Rational Expressions Sheet & Answer Key

Students will practice adding rational expressions and subtracting rational expressions .

Note: This page's worksheet focuses on adding rational expressions with like denominators .

We also have a separate worksheet on adding and subtracting rational expressions that have unlike denominators .

Example Questions

II. Directions: Add and Subtract the Rational Expressions below

Challenge Problem

Other Details

This is a 4 part worksheet:

• Part I Model Problems
• Part II Practice
• Part III Challenge Problems
• Part IV Answer Key
• Rational Expressions
• How to Add and Subtract Rational Expressions

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• $ 0.00 0 items

Add and Subtract Rational Expressions

7.2 add and subtract rational expressions.

Topics covered in this section are:

• Add and subtract rational expressions with a common denominator
• Add and subtract rational expressions whose denominators are opposites
• Find the least common denominator of rational expressions
• Add and subtract rational expressions with unlike denominators
• Add and subtract rational functions

7.2.1 Add and Subtract Rational Expressions with a Common Denominator

What is the first step you take when you add numerical fractions? You check if they have a common denominator. If they do, you add the numerators and place the sum over the common denominator. If they do not have a common denominator, you find one before you add.

It is the same with rational expressions. To add rational expressions, they must have a common denominator. When the denominators are the same, you add the numerators and place the sum over the common denominator.

RATIONAL EXPRESSION ADDITION AND SUBTRACTION

If $p$, $q$, and $r$ are polynomials where $r≠0$, then

$\frac{p}{r}+\frac{q}{r}=\frac{p+q}{r}$ and $\frac{p}{r}-\frac{q}{r}=\frac{p-q}{r}$

To add or subtract rational expressions with a common denominator, add or subtract the numerators and place the result over the common denominator.

We always simplify rational expressions. Be sure to factor, if possible, after you subtract the numerators so you can identify any common factors.

Remember, too, we do not allow values that would make the denominator zero. What value of $x$ should be excluded in the next example?

Add: $\frac{11x+28}{x+4}+\frac{x^{2}}{x+4}$.

Since the denominator is $x+4$, we must exclude the value $x=-4$.

The expression simplifies to $x+7$ but the original expression had a denominator of $x+4$ so $x≠-4$.

To subtract rational expressions, they must also have a common denominator. When the denominators are the same, you subtract the numerators and place the difference over the common denominator. Be careful of the signs when you subtract a binomial or trinomial.

Subtract: $\frac{5x^{2}-7x+3}{x^{2}-3x-18}-\frac{4x^{2}+x-9}{x^{2}-3x-18}$.

7.2.2 Add and Subtract Rational Expressions Whose Denominators are Opposites

When the denominators of two rational expressions are opposites, it is easy to get a common denominator. We just have to multiply one of the fractions by $\frac{-1}{-1}$. Let’s see how this works.

Be careful with the signs as you work with the opposites when the fractions are being subtracted.

Subtract: $\frac{m^{2}-6m}{m^{2}-1}-\frac{3m+2}{1-m^{2}}$.

7.2.3 Find the Least Common Denominator of Rational Expressions

When we add or subtract rational expressions with unlike denominators, we will need to get common denominators. If we review the procedure we used with numerical fractions, we will know what to do with rational expressions.

Let’s look at this example: $\frac{7}{12}+\frac{5}{18}$. Since the denominators are not the same, the first step was to find the least common denominator (LCD).

To find the LCD of the fractions, we factored $12$ and $18$ into primes, lining up any common primes in columns. Then we “brought down” one prime from each column. Finally, we multiplied the factors to find the LCD.

When we add numerical fractions, once we found the LCD, we rewrote each fraction as an equivalent fraction with the LCD by multiplying the numerator and denominator by the same number. We are now ready to add.

We do the same thing for rational expressions. However, we leave the LCD in factored form.

HOW TO: Find the least common denominator of rational expressions.

• Factor each denominator completely.
• List the factors of each denominator. Match factors vertically when possible.
• Bring down the columns by including all factors, but do not include common factors twice.
• Write the LCD as the product of the factors.

Remember, we always exclude values that would make the denominator zero. What values of $x$ should we exclude in this next example?

a) Find the LCD for the expressions $\frac{8}{x^{2}-2x-3}$, $\frac{3x}{x^{2}+4x+3}$, and b) rewrite them as equivalent rational expressions with the lowest common denominator.

7.2.4 Add and Subtract Rational Expressions with Unlike Denominators

Now we have all the steps we need to add or subtract rational expressions with unlike denominators.

Add: $\frac{3}{x-3} + \frac{2}{x-2}$.

The steps used to add rational expressions are summarized here.

HOW TO: Add or subtract rational expressions.

• Yes  – go to step 2.
• Find the LCD.
• Rewrite each rational expression as an equivalent rational expression with the LCD.
• Add or subtract the rational expressions.
• Simplify, if possible.

Avoid the temptation to simplify too soon. In the example above, we must leave the first rational expression as $\frac{3x-6}{(x-3)(x-2)}$ to be able to add it to $\frac{2x-6}{(x-2)(x-3)}$. Simplify only after you have combined the numerators.

Add: $\frac{8}{x^{2}-2x-3} + \frac{3x}{x^{2}+4x+3}$.

The process we use to subtract rational expressions with different denominators is the same as for addition. We just have to be very careful of the signs when subtracting the numerators.

Subtract: $\frac{8y}{y^{2}-16}-\frac{4}{y-4}$.

There are a lot of negative signs in the next example. Be extra careful.

Subtract: $\frac{-3n-9}{n^{2}+n-6}-\frac{n+3}{2-n}$.

Things can get very messy when both fractions must by multiplied by a binomial to get the common denominator.

Subtract: $\frac{4}{a^{2}+6a+5}-\frac{3}{a^{2}+7a+10}$.

We follow the same steps as before to find the LCD when we have more than two rational expressions. In the next example, we will start by factoring all three denominators to find their LCD.

Simplify: $\frac{2u}{u-1}+\frac{1}{u}-\frac{2u-1}{u^{2}-u}$.

7.2.5 Add and Subtract Rational Functions

To add or subtract rational functions, we use the same techniques we used to add or subtract polynomial functions.

Find $R(x)=f(x)-g(x)$ where $f(x)=\frac{x+5}{x-2}$ and $g(x)=\frac{5x+18}{x^{2}-4}$.

CC Licensed Content, Original

• Revision and Adaption. Provided by: Minute Math. License:  CC BY 4.0

CC Licensed Content, Shared Previously

• Marecek, L., & Mathis, A. H. (2020). Add and Subtract Rational Expressions. In Intermediate Algebra 2e. OpenStax.    https://openstax.org/books/intermediate-algebra-2e/pages/7-2-add-and-subtract-rational-expressions .  License:  CC BY 4.0 . Access for free at  https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

Share this:

• No products in the cart.

Adding and Subtracting Rational Expressions

More specific topics in adding and subtracting rational expressions.

• Adding and Subtracting with Like Denominators
• Adding and Subtracting with Unlike Denominators

Popular Tutorials in Adding and Subtracting Rational Expressions

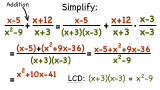
How Do You Add Two Rational Expressions with Different Denominators?

Adding rational expressions together? Don't have common denominators? No problem! Find the least common denominator (LCD) and change each rational expression into an equivalent expression with that LCD. Once you have common denominators, you're ready to add and simplify! Watch it all in this tutorial!

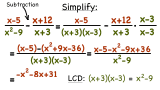
How Do You Subtract Two Rational Expressions with Different Denominators?

Subtracting rational expressions? Don't have common denominators? No problem! Find the least common denominator (LCD) and change each rational expression into an equivalent expression with that LCD. Once you have common denominators, you're ready to subtract and simplify! Watch it all in this tutorial!

How Do You Find the Least Common Denominator of Two Rational Expressions?

When adding or subtracting rational expressions, you need have common denominators just like any other fraction. If you don't have common denominators, then you'll need to find the least common denominator (LCD) and use it to get those denominators to be the same. Learn how to find the LCD of two rational expressions by watching this tutorial!

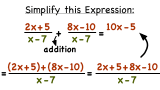
How Do You Add Two Rational Expressions with the Same Denominator?

Adding rational expressions together? If they have a common denominator, just add the numerators together and simplify. Just like you would with any other fractions! Watch the process in this tutorial.

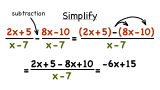
How Do You Subtract Two Rational Expressions with the Same Denominator?

Subtracting rational expressions? If they have a common denominator, just subtract the numerators and simplify. Just like you would with any other fractions! Watch the process in this tutorial.

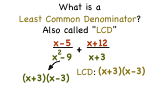
What's the Least Common Denominator?

When you're working with fractions, you may need to find the least common denominator (LCD) in order to get the fractions to have a common denominator so that you can add or subtract them. The LCD is the smallest multiple that the denominators have in common. Learn about the LCD in this tutorial!

How Do You Find the Least Common Multiple of Monomials?

Looking for practice finding the least common multiple (LCM) of monomials? Then be sure to check out this tutorial! Follow along with this tutorial as it goes through the process of using prime factorization to help find the LCM. Check it out!

Related Topics

Other topics in rational expressions and functions :.

• Inverse Variation
• Rational Functions
• Rational Expressions
• Multiplying and Dividing Rational Expressions
• Dividing Polynomials
• Mixed Expressions and Complex Fractions
• Solve Rational Equations
• Terms of Use

8.3 Add and Subtract Rational Expressions with a Common Denominator

Learning objectives.

By the end of this section, you will be able to:

• Add rational expressions with a common denominator
• Subtract rational expressions with a common denominator
• Add and subtract rational expressions whose denominators are opposites

Be Prepared 8.9

Before you get started, take this readiness quiz.

If you miss a problem, go back to the section listed and review the material.

Add: y 3 + 9 3 . y 3 + 9 3 . If you missed this problem, review Example 1.77 .

Be Prepared 8.10

Subtract: 10 x − 2 x . 10 x − 2 x . If you missed this problem, review Example 1.79 .

Be Prepared 8.11

Factor completely: 8 n 5 − 20 n 3 . 8 n 5 − 20 n 3 . If you missed this problem, review Example 7.59 .

Be Prepared 8.12

Factor completely: 45 a 3 − 5 a b 2 . 45 a 3 − 5 a b 2 . If you missed this problem, review Example 7.62 .

Add Rational Expressions with a Common Denominator

What is the first step you take when you add numerical fractions? You check if they have a common denominator. If they do, you add the numerators and place the sum over the common denominator. If they do not have a common denominator, you find one before you add.

It is the same with rational expressions. To add rational expressions, they must have a common denominator. When the denominators are the same, you add the numerators and place the sum over the common denominator.

Rational Expression Addition

If p , q , and r p , q , and r are polynomials where r ≠ 0 r ≠ 0 , then

To add rational expressions with a common denominator, add the numerators and place the sum over the common denominator.

We will add two numerical fractions first, to remind us of how this is done.

Example 8.30

Add: 5 18 + 7 18 . 5 18 + 7 18 .

Try It 8.59

Add: 7 16 + 5 16 . 7 16 + 5 16 .

Try It 8.60

Add: 3 10 + 1 10 . 3 10 + 1 10 .

Remember, we do not allow values that would make the denominator zero. What value of y y should be excluded in the next example?

Example 8.31

Add: 3 y 4 y − 3 + 7 4 y − 3 . 3 y 4 y − 3 + 7 4 y − 3 .

The numerator and denominator cannot be factored. The fraction is simplified.

Try It 8.61

Add: 5 x 2 x + 3 + 2 2 x + 3 . 5 x 2 x + 3 + 2 2 x + 3 .

Try It 8.62

Add: x x − 2 + 1 x − 2 . x x − 2 + 1 x − 2 .

Example 8.32

Add: 7 x + 12 x + 3 + x 2 x + 3 . 7 x + 12 x + 3 + x 2 x + 3 .

Try It 8.63

Add: 9 x + 14 x + 7 + x 2 x + 7 . 9 x + 14 x + 7 + x 2 x + 7 .

Try It 8.64

Add: x 2 + 8 x x + 5 + 15 x + 5 . x 2 + 8 x x + 5 + 15 x + 5 .

Subtract Rational Expressions with a Common Denominator

To subtract rational expressions, they must also have a common denominator. When the denominators are the same, you subtract the numerators and place the difference over the common denominator.

Rational Expression Subtraction

To subtract rational expressions, subtract the numerators and place the difference over the common denominator.

We always simplify rational expressions. Be sure to factor, if possible, after you subtract the numerators so you can identify any common factors.

Example 8.33

Subtract: n 2 n − 10 − 100 n − 10 . n 2 n − 10 − 100 n − 10 .

Try It 8.65

Subtract: x 2 x + 3 − 9 x + 3 . x 2 x + 3 − 9 x + 3 .

Try It 8.66

Subtract: 4 x 2 2 x − 5 − 25 2 x − 5 . 4 x 2 2 x − 5 − 25 2 x − 5 .

Be careful of the signs when you subtract a binomial!

Example 8.34

Subtract: y 2 y − 6 − 2 y + 24 y − 6 . y 2 y − 6 − 2 y + 24 y − 6 .

Try It 8.67

Subtract: n 2 n − 4 − n + 12 n − 4 . n 2 n − 4 − n + 12 n − 4 .

Try It 8.68

Subtract: y 2 y − 1 − 9 y − 8 y − 1 . y 2 y − 1 − 9 y − 8 y − 1 .

Example 8.35

Subtract: 5 x 2 − 7 x + 3 x 2 − 3 x – 18 − 4 x 2 + x − 9 x 2 − 3 x – 18 . 5 x 2 − 7 x + 3 x 2 − 3 x – 18 − 4 x 2 + x − 9 x 2 − 3 x – 18 .

Try It 8.69

Subtract: 4 x 2 − 11 x + 8 x 2 − 3 x + 2 − 3 x 2 + x − 3 x 2 − 3 x + 2 . 4 x 2 − 11 x + 8 x 2 − 3 x + 2 − 3 x 2 + x − 3 x 2 − 3 x + 2 .

Try It 8.70

Subtract: 6 x 2 − x + 20 x 2 − 81 − 5 x 2 + 11 x − 7 x 2 − 81 . 6 x 2 − x + 20 x 2 − 81 − 5 x 2 + 11 x − 7 x 2 − 81 .

Add and Subtract Rational Expressions whose Denominators are Opposites

When the denominators of two rational expressions are opposites, it is easy to get a common denominator. We just have to multiply one of the fractions by −1 −1 −1 −1 .

Let’s see how this works.

Example 8.36

Add: 4 u − 1 3 u − 1 + u 1 − 3 u . 4 u − 1 3 u − 1 + u 1 − 3 u .

Try It 8.71

Add: 8 x − 15 2 x − 5 + 2 x 5 − 2 x . 8 x − 15 2 x − 5 + 2 x 5 − 2 x .

Try It 8.72

Add: 6 y 2 + 7 y − 10 4 y − 7 + 2 y 2 + 2 y + 11 7 − 4 y . 6 y 2 + 7 y − 10 4 y − 7 + 2 y 2 + 2 y + 11 7 − 4 y .

Example 8.37

Subtract: m 2 − 6 m m 2 − 1 − 3 m + 2 1 − m 2 . m 2 − 6 m m 2 − 1 − 3 m + 2 1 − m 2 .

Try It 8.73

Subtract: y 2 − 5 y y 2 − 4 − 6 y − 6 4 − y 2 . y 2 − 5 y y 2 − 4 − 6 y − 6 4 − y 2 .

Try It 8.74

Subtract: 2 n 2 + 8 n − 1 n 2 − 1 − n 2 − 7 n − 1 1 − n 2 . 2 n 2 + 8 n − 1 n 2 − 1 − n 2 − 7 n − 1 1 − n 2 .

Section 8.3 Exercises

Practice makes perfect.

In the following exercises, add.

2 15 + 7 15 2 15 + 7 15

4 21 + 3 21 4 21 + 3 21

7 24 + 11 24 7 24 + 11 24

7 36 + 13 36 7 36 + 13 36

3 a a − b + 1 a − b 3 a a − b + 1 a − b

3 c 4 c − 5 + 5 4 c − 5 3 c 4 c − 5 + 5 4 c − 5

d d + 8 + 5 d + 8 d d + 8 + 5 d + 8

7 m 2 m + n + 4 2 m + n 7 m 2 m + n + 4 2 m + n

p 2 + 10 p p + 2 + 16 p + 2 p 2 + 10 p p + 2 + 16 p + 2

q 2 + 12 q q + 3 + 27 q + 3 q 2 + 12 q q + 3 + 27 q + 3

2 r 2 2 r − 1 + 15 r − 8 2 r − 1 2 r 2 2 r − 1 + 15 r − 8 2 r − 1

3 s 2 3 s − 2 + 13 s − 10 3 s − 2 3 s 2 3 s − 2 + 13 s − 10 3 s − 2

8 t 2 t + 4 + 32 t t + 4 8 t 2 t + 4 + 32 t t + 4

6 v 2 v + 5 + 30 v v + 5 6 v 2 v + 5 + 30 v v + 5

2 w 2 w 2 − 16 + 8 w w 2 − 16 2 w 2 w 2 − 16 + 8 w w 2 − 16

7 x 2 x 2 − 9 + 21 x x 2 − 9 7 x 2 x 2 − 9 + 21 x x 2 − 9

In the following exercises, subtract.

y 2 y + 8 − 64 y + 8 y 2 y + 8 − 64 y + 8

z 2 z + 2 − 4 z + 2 z 2 z + 2 − 4 z + 2

9 a 2 3 a − 7 − 49 3 a − 7 9 a 2 3 a − 7 − 49 3 a − 7

25 b 2 5 b − 6 − 36 5 b − 6 25 b 2 5 b − 6 − 36 5 b − 6

c 2 c − 8 − 6 c + 16 c − 8 c 2 c − 8 − 6 c + 16 c − 8

d 2 d − 9 − 6 d + 27 d − 9 d 2 d − 9 − 6 d + 27 d − 9

3 m 2 6 m − 30 − 21 m − 30 6 m − 30 3 m 2 6 m − 30 − 21 m − 30 6 m − 30

2 n 2 4 n − 32 − 18 n − 16 4 n − 32 2 n 2 4 n − 32 − 18 n − 16 4 n − 32

6 p 2 + 3 p + 4 p 2 + 4 p − 5 − 5 p 2 + p + 7 p 2 + 4 p − 5 6 p 2 + 3 p + 4 p 2 + 4 p − 5 − 5 p 2 + p + 7 p 2 + 4 p − 5

5 q 2 + 3 q − 9 q 2 + 6 q + 8 − 4 q 2 + 9 q + 7 q 2 + 6 q + 8 5 q 2 + 3 q − 9 q 2 + 6 q + 8 − 4 q 2 + 9 q + 7 q 2 + 6 q + 8

5 r 2 + 7 r − 33 r 2 − 49 − 4 r 2 + 5 r + 30 r 2 − 49 5 r 2 + 7 r − 33 r 2 − 49 − 4 r 2 + 5 r + 30 r 2 − 49

7 t 2 − t − 4 t 2 − 25 − 6 t 2 + 12 t − 44 t 2 − 25 7 t 2 − t − 4 t 2 − 25 − 6 t 2 + 12 t − 44 t 2 − 25

10 v 2 v − 1 + 2 v + 4 1 − 2 v 10 v 2 v − 1 + 2 v + 4 1 − 2 v

20 w 5 w − 2 + 5 w + 6 2 − 5 w 20 w 5 w − 2 + 5 w + 6 2 − 5 w

10 x 2 + 16 x − 7 8 x − 3 + 2 x 2 + 3 x − 1 3 − 8 x 10 x 2 + 16 x − 7 8 x − 3 + 2 x 2 + 3 x − 1 3 − 8 x

6 y 2 + 2 y − 11 3 y − 7 + 3 y 2 − 3 y + 17 7 − 3 y 6 y 2 + 2 y − 11 3 y − 7 + 3 y 2 − 3 y + 17 7 − 3 y

z 2 + 6 z z 2 − 25 − 3 z + 20 25 − z 2 z 2 + 6 z z 2 − 25 − 3 z + 20 25 − z 2

a 2 + 3 a a 2 − 9 − 3 a − 27 9 − a 2 a 2 + 3 a a 2 − 9 − 3 a − 27 9 − a 2

2 b 2 + 30 b − 13 b 2 − 49 − 2 b 2 − 5 b − 8 49 − b 2 2 b 2 + 30 b − 13 b 2 − 49 − 2 b 2 − 5 b − 8 49 − b 2

c 2 + 5 c − 10 c 2 − 16 − c 2 − 8 c − 10 16 − c 2 c 2 + 5 c − 10 c 2 − 16 − c 2 − 8 c − 10 16 − c 2

Everyday Math

Sarah ran 8 miles and then biked 24 miles. Her biking speed is 4 mph faster than her running speed. If r r represents Sarah’s speed when she ran, then her running time is modeled by the expression 8 r 8 r and her biking time is modeled by the expression 24 r + 4 . 24 r + 4 . Add the rational expressions 8 r + 24 r + 4 8 r + 24 r + 4 to get an expression for the total amount of time Sarah ran and biked.

If Pete can paint a wall in p p hours, then in one hour he can paint 1 p 1 p of the wall. It would take Penelope 3 hours longer than Pete to paint the wall, so in one hour she can paint 1 p + 3 1 p + 3 of the wall. Add the rational expressions 1 p + 1 p + 3 1 p + 1 p + 3 to get an expression for the part of the wall Pete and Penelope would paint in one hour if they worked together.

Writing Exercises

Donald thinks that 3 x + 4 x 3 x + 4 x is 7 2 x . 7 2 x . Is Donald correct? Explain.

Explain how you find the Least Common Denominator of x 2 + 5 x + 4 x 2 + 5 x + 4 and x 2 − 16 . x 2 − 16 .

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Elementary Algebra 2e
• Publication date: Apr 22, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra-2e/pages/8-3-add-and-subtract-rational-expressions-with-a-common-denominator

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

Algebra II : Adding and Subtracting Rational Expressions

Study concepts, example questions & explanations for algebra ii, all algebra ii resources, example questions, example question #1 : adding and subtracting rational expressions.

Find the least common denominator (LCD) and convert each fraction to the LCD, then add the numerators.  Simplify as needed.

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

Because the two rational expressions have the same denominator, we can simply add straight across the top.  The denominator stays the same.

Example Question #1 : Solving Rational Expressions

The expression cannot be simplified.

c. Subtract the numerators, putting the difference over the common denominator.

Example Question #2 : Solving Rational Expressions

Combine the following expression into one fraction:

The two fractions cannot be combined as they have different denominators.

Since these fractions have the same denominators, we can now combine them, and our final answer is therefore:

Example Question #3 : Solving Rational Expressions

We start by adjusting both terms to the same denominator which is 2 x 3 = 6

Then we adjust the numerators by multiplying x+1 by 2 and 2x-5 by 3

The results are:

So the final answer is,

Example Question #4 : Solving Rational Expressions

Start by putting both equations at the same denominator. 

2x+4 = (x+2) x 2 so we only need to adjust the first term: 

Then we subtract the numerators, remembering to distribute the negative sign to all terms of the second fraction's numerator:

(x+5)(x+3) is the common denominator for this problem making the numerators 7(x+3) and 8(x+5).

7(x+3)+8(x+5)= 7x+21+8x+40= 15x+61

Example Question #7 : How To Add Polynomials

First factor the denominators which gives us the following:

The two rational fractions have a common denominator hence they are like "like fractions".  Hence we get:

Simplifying gives us

Example Question #6 : Solving Rational Expressions

First let us find a common denominator as follows:

Example Question #6 : How To Find The Solution To A Rational Equation With Lcd

Solve the rational equation:

no solution

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \frac{6}{x-1}+\frac{3}{x+1}
• \frac{2}{x^2-36}-\frac{1}{x^2+6x}
• \frac{6x}{7}\cdot \frac{4x}{3}
• \frac{\frac{6x}{7}}{\frac{4x}{3}}
• \frac{x-3}{5x-15}
• What is a rational expression in math?
• A rational expression is an expression that is the ratio of two polynomial expressions.
• How do you identify rational expressions?
• To identify a rational expression, factor the numerator and denominator into their prime factors and cancel out any common factors that you find. If you are left with a fraction with polynomial expressions in the numerator and denominator, then the original expression is a rational expression. If not, then it is not a rational expression.
• Why is it called a rational expression?
• A rational expression is called a 'rational' expression because it can be written as a fraction, with the polynomial expression in the numerator and the polynomial expression in the denominator. The term 'rational' refers to the fact that the expression can be written as a ratio of two expressions (The term 'rational' comes from the Latin word 'ratio').
• What are the 4 types of rational numbers?
• There are four types of rational numbers: positive rational numbers (greater than zero), negative rational numbers (less than zero),non-negative rational numbers (greater than or equal to zero), and non-positive rational numbers (less than or equal to zero).
• How do you solve rational expressions step by step?
• To solve a rational expression start by simplifying the expression by finding a common factor in the numerator and denominator and canceling it out. Then, check for extraneous solutions, which are values of the variable that makes the denominator equal to zero. These solutions must be excluded because they are not valid solutions to the equation. Solve the resulting equation for the variable by using techniques such as factoring, using the quadratic formula, or completing the square.

rational-expression-calculator

• High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables. In this blog post,...

Please add a message.

Message received. Thanks for the feedback.

Search Utah State University:

Rational expressions, introduction.

A review of reduction, multiplication, division, addition and subtraction of rational expressions

The Essentials

When reducing a rational expression, first factor the numerator and denominator. Next, note the numbers that make the denominator equal to zero and cancel identical terms:

Here we note that x = 3 and x = 1 make it so that this expression doesn’t exist. Canceling gives us:

When multiplying rational expressions, the terms can just be combined and reduced as one fraction. When dividing rational expressions, just flip the divisor, combine the expressions, and reduce them:

Flipping and combining gives us:

Here we note that \( x = 5,−1,−3,−7 \) make the expression non-existent.

When adding or subtracting rational expressions, the denominators need to be factored. After they are factored it’s easy to see what is needed to make the denominators equal:

The numerators are distributed and combined while the denominator stays factored:

Find x in the following rational expression:

Here note that the equation is undefined at \( x = −5, 4 \)

The numbers -5 and 1 are solutions to this equation. However, as noted above -5 makes the equation undefined and is therefore an extraneous solution making 1 the only solution.

Evaluate this expression and determine if any of the solutions are extraneous:

\( x = 0, 3 \) where \( x = 3 \) is an extraneous solution

More Resources

• Khan Academy: Rational expressions