experiment buffon needle

Buffon's Needle Problem

(OEIS A060294 ).

where (Uspensky 1937, pp. 252 and 258; Kunkel).

then gives the plot illustrated above. The above can be derived by noting that

which is both a uniformly minimum variance unbiased estimator and a maximum likelihood estimator (Perlman and Wishura 1975) with variance

(OEIS A114598 ; Mantel 1953; Solomon 1978, p. 7).

A further generalization obtained by throwing a needle on a board ruled with two sets of perpendicular lines is called the Buffon-Laplace needle problem .

Explore with Wolfram|Alpha

More things to try:

• probability
• 32 coin tosses
• corners of x + 2 |sin x|

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Buffon's Needle Problem." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/BuffonsNeedleProblem.html

Subject classifications

College of Education

Office for Mathematics, Science, and Technology Education

• MSTE Personnel
• MSTE History
• Featured Projects
• Past Projects
• Contact MSTE
• Directions to MSTE
• Contact Form

Buffon's Needle

• 3 Also known as
• 5 Source of Name
• 6 Historical Note

Let a horizontal plane be divided into strips by a series of parallel lines a fixed distance apart, like floorboards.

Let a needle whose length equals the distance between the parallel lines be dropped onto the plane randomly from a random height .

Then the probability that the needle falls across one of the parallel lines is $\dfrac 2 \pi$.

For simplicity, consider the real number plane $\R^2$ divided into strips by the lines $x = k$ for each integer $k$.

Then the needle would have length $1$, which is the distance between the lines .

Define $\theta \in \hointr {-\dfrac \pi 2} {\dfrac \pi 2}$ as the angle between the needle and the $x$-axis .

Then the horizontal component of length of the needle is $\cos \theta$ for each $\theta$.

Let the needle drop.

Without loss of generality , let the end with the larger $x$-coordinate have $x$-coordinate $0 \le x_n < 1$.

Then for each $\theta$, the needle falls across the line $x = 0$ exactly when $0 \le x_n \le \cos \theta$.

Therefore the probability that this happens is:

By considering $\theta$ as a continuous random variable ,

$\blacksquare$

Also known as

The problem of Buffon's Needle , along with the Buffon-Laplace Problem , is also known just as the Needle Problem .

• Buffon-Laplace Problem

Source of Name

This entry was named for Georges Louis Leclerc, Comte de Buffon .

Historical Note

Georges Louis Leclerc, Comte de Buffon published this problem in his Histoire Naturelle in $1777$.

Pierre-Simon de Laplace extended the problem to a general rectangular grid, thus creating what is now sometimes referred to as the Buffon-Laplace Problem .

Augustus De Morgan reports that a pupil of his once performed a practical experiment using Buffon's Needle to calculate a value for $\pi$ .

After $600$ trials, a value of $3.137$ was obtained.

• 1986:  David Wells : Curious and Interesting Numbers  ... (previous)  ... (next) : $3 \cdotp 14159 \, 26535 \, 89793 \, 23846 \, 26433 \, 83279 \, 50288 \, 41972 \ldots$
• 1997:  David Wells : Curious and Interesting Numbers  (2nd ed.)  ... (previous)  ... (next) : $3 \cdotp 14159 \, 26535 \, 89793 \, 23846 \, 26433 \, 83279 \, 50288 \, 41971 \ldots$
• 1998:  David Nelson : The Penguin Dictionary of Mathematics  (2nd ed.)  ... (previous)  ... (next) : Buffon's needle problem
• 2008:  David Nelson : The Penguin Dictionary of Mathematics  (4th ed.)  ... (previous)  ... (next) : Buffon's needle problem
• 2014:  Christopher Clapham  and James Nicholson : The Concise Oxford Dictionary of Mathematics  (5th ed.)  ... (previous)  ... (next) : Buffon's needle
• Expansion Required
• Proven Results
• Named Theorems/Buffon
• Buffon's Needle
• Trigonometry

Navigation menu

Activity: Buffon's Needle

How to estimate Pi  by dropping a match.

A few hundred years ago people enjoyed betting on coins tossed on to the floor : would the coin cross a line or not?

A man (Georges-Louis Leclerc, the Count of Buffon ) started thinking about this and worked out the probability .

It is called "Buffon's Needle" in his honor.

Now it is your turn to have a go!

You will need:

• Measure the spacing of your lines (it may not print at exactly 50mm): ____ mm
• Measure the length of your match (must be less than the line spacing): ____ mm
• Make sure your sheet of paper is on a flat surface such as a table top or the floor.

The exact height from which you drop the match is not important, but don't drop it so close to the paper that you are cheating!

If the match rolls completely off the paper, then do not count that turn.

Now we will drop the match 100 times, but first ...

... what percentage do you think will land A, or B?

Make a guess (estimate) before you begin the experiment:

OK let's begin .

Drop the match 100 times and record A (does not touch a grid line) or B (touches or crosses a grid line) using Tally Marks :

Now draw a Bar Graph to illustrate your results. You can create one at Data Graphs (Bar, Line and Pie) .

• Are the bars the same height?
• Did you expect them to be?
• How does the result compare with your guess?

Now Let's Estimate Pi

Buffon used the results from his experiment with a needle to estimate the value of π ( Pi ). He worked out this formula:

• L is the length of the needle (or match in our case)
• x is the line spacing (50 mm for us)
• p is the proportion of needles crossing a line (case B)

We can do it too!

Example: Sam had a match of length 31 mm, and a 40 mm line spacing and 49 of 100 drops crossed the line

So Sam had:

• p = 49/100 = 0.49

Substituting these values into the formula, Sam got:

π ≈ 2 × 31 40 × 0.49  ≈ 3.16

Now it's your turn. Fill in the following table using your own results:

And do the calculation:

π   ≈   2L xp   ≈   2 × _____ _____ × _____   ≈  _____

Did you do any better?

It won't be exact (because it is a random thing) but it may be close.

Changing The Subject

The next part of this activity is to " change the subject " of the formula to work out the perfect value of "p" (the proportion of times the match crosses the line):

And we get:

p  ≈   2L π x

Example: Alex had a match of length 36 mm, and a 50 mm line spacing.

So Alex had:

Substituting these values into the formula, Alex got:

p  ≈   2 × 36 π × 50   ≈  0.46...

So Alex should expect the match to cross the line (case B) 46 times out of 100

Fill in the following table using your own results:

How close were you?

Different Size of Match

Try repeating the experiment using a different sized match (but not larger then the line spacing!)

• Did you get better or worse results?

What You Have Done

You have (hopefully) had fun running an experiment .

You have had some experience with calculations.

And you have seen the relationship between theory and reality.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.1: Buffon's Problems

• Last updated
• Save as PDF
• Page ID 10222

• Kyle Siegrist
• University of Alabama in Huntsville via Random Services

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Buffon's experiments are very old and famous random experiments, named after comte de Buffon. These experiments are considered to be among the first problems in geometric probability.

Buffon's Coin Experiment

Buffon's coin experiment consists of dropping a coin randomly on a floor covered with identically shaped tiles. The event of interest is that the coin crosses a crack between tiles. We will model Buffon's coin problem with square tiles of side length 1—assuming the side length is 1 is equivalent to taking the side length as the unit of measurement.

Assumptions

First, let us define the experiment mathematically. As usual, we will idealize the physical objects by assuming that the coin is a perfect circle with radius \(r\) and that the cracks between tiles are line segments. A natural way to describe the outcome of the experiment is to record the center of the coin relative to the center of the tile where the coin happens to fall. More precisely, we will construct coordinate axes so that the tile where the coin falls occupies the square \( S = \left[ -\frac{1}{2}, \frac{1}{2} \right]^2 \).

Now when the coin is tossed, we will denote the center of the coin by \((X, Y) \in S\) so that \(S\) is our sample space and \(X\) and \(Y\) are our basic random variables. Finally, we will assume that \(r \lt \frac{1}{2}\) so that it is at least possible for the coin to fall inside the square without touching a crack.

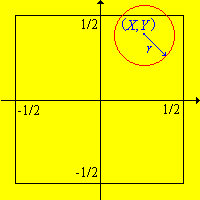
Next, we need to define an appropriate probability measure that describes our basic random vector \((X, Y)\). If the coin falls randomly on the floor, then it is natural to assume that \((X, Y)\) is uniformly distributed on \(S\). By definition, this means that

\[ \P[(X, Y) \in A] = \frac{\area(A)}{\area(S)}, \quad A \subseteq S \]

Run Buffon's coin experiment with the default settings. Watch how the points seem to fill the sample space \(S\) in a uniform manner.

The Probability of a Crack Crossing

Our interest is in the probability of the event \(C\) that the coin crosses a crack.

The probability of a crack crossing is \(\P(C) - 1 - (1 - 2 r)^2\).

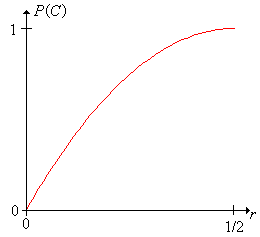
In Buffon's coin experiment, change the radius with the scroll bar and watch how the events \(C\) and \(C^c\) and change. Run the experiment with various values of \(r\) and compare the physical experiment with the points in the scatterplot. Compare the relative frequency of \(C\) to the probability of \(C\).

The convergence of the relative frequency of an event (as the experiment is repeated) to the probability of the event is a special case of the law of large numbers.

Solve Buffon's coin problem with rectangular tiles that have height \(h\) and width \(w\).

\[1 - \frac{(h - 2 \, r)(w - 2 \, r)}{h \, w}, \quad r \lt \min \left\{ \frac{h}{2}, \frac{w}{2} \right\}\]

Solve Buffon's coin problem with equilateral triangular tiles that have side length 1.

Recall that random numbers are simulation of independent random variables, each with the standard uniform distribution, that is, the continuous uniform distribution on the interval \( (0, 1) \).

Show how to simulate the center of the coin \((X, Y)\) in Buffon's coin experiment using random numbers.

\(X = U - \frac{1}{2}\), \(Y = V - \frac{1}{2}\), where \(U\) and \(V\) are random numbers.

Buffon's Needle Problem

Buffon's needle experiment consists of dropping a needle on a hardwood floor. The main event of interest is that the needle crosses a crack between floorboards. Strangely enough, the probability of this event leads to a statistical estimate of the number \(\pi\)!

Our first step is to define the experiment mathematically. Again we idealize the physical objects by assuming that the floorboards are uniform and that each has width 1. We will also assume that the needle has length \(L \lt 1\) so that the needle cannot cross more than one crack. Finally, we assume that the cracks between the floorboards and the needle are line segments.

When the needle is dropped, we want to record its orientation relative to the floorboard cracks. One way to do this is to record the angle \(X\) that the top half of the needle makes with the line through the center of the needle, parallel to the floorboards, and the distance \(Y\) from the center of the needle to the bottom crack. These will be the basic random variables of our experiment, and thus the sample space of the experiment is \[ S = [0, \pi) \times [0, 1) = \{(x, y): 0 \le x \lt \pi, \; 0 \le y \lt 1\} \]

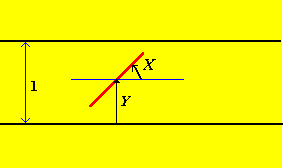
Again, our main modeling assumption is that the needle is tossed randomly on the floor. Thus, a reasonable mathematical assumption might be that the basic random vector \((X, Y)\) is uniformly distributed over the sample space. By definition, this means that \[ \P[(X, Y) \in A] = \frac{\area(A)}{\area(S)}, \quad A \subseteq S \]

Run Buffon's needle experiment with the default settings and watch the outcomes being plotted in the sample space. Note how the points in the scatterplot seem to fill the sample space \(S\) in a uniform way.

Our main interest is in the event \(C\) that the needle crosses a crack between the floorboards.

The event \(C\) can be written in terms of the basic angle and distance variables as follows: \[ C = \left\{ Y \lt \frac{L}{2} \, \sin(X) \right\} \cup \left\{ Y \gt 1 - \frac{L}{2} \, \sin(X) \right\} \]

The curves \(y = \frac{L}{2} \, \sin(x)\) and \(y = 1 - \frac{L}{2} \, \sin(x)\) on the interval \(0 \le x \lt \pi\) are shown in blue in the scatterplot of Buffon's needle experiment, and hence event \(C\) is the union of the regions below the lower curve and above the upper curve. Thus, the needle crosses a crack precisely when a point falls in this region.

The probability of a crack crossing is \(\P(C) = 2 L / \pi\).

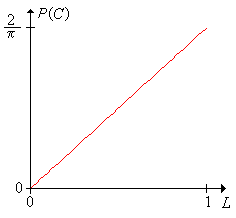
In the Buffon's needle experiment, vary the needle length \(L\) with the scroll bar and watch how the event \(C\) changes. Run the experiment with various values of \(L\) and compare the physical experiment with the points in the scatterplot. Compare the relative frequency of \(C\) to the probability of \(C\).

Find the probabilities of the following events in Buffon's needle experiment. In each case, sketch the event as a subset of the sample space.

• \(\{0 \lt X \lt \pi / 2, \; 0 \lt Y \lt 1 / 3\}\)
• \(\{1 / 4 \lt Y \lt 2 / 3\}\)
• \(\{X \lt Y\}\)
• \(\{X + Y \lt 2\}\)
• \(\frac{1}{6}\)
• \(\frac{5}{12}\)
• \(\frac{1}{2 \pi}\)
• \(\frac{3}{2 \pi}\)

The Estimate of \( \pi \)

Suppose that we run Buffon's needle experiment a large number of times. By the law of large numbers, the proportion of crack crossings should be about the same as the probability of a crack crossing. More precisely, we will denote the number of crack crossings in the first \(n\) runs by \(N_n\). Note that \(N_n\) is a random variable for the compound experiment that consists of \(n\) replications of the basic needle experiment. Thus, if \(n\) is large, we should have \( \frac{N_n}{n} \approx \frac{2 L}{\pi} \) and hence \[ \pi \approx \frac{2 L n}{N_n} \] This is Buffon's famous estimate of \(\pi\). In the simulation of Buffon's needle experiment, this estimate is computed on each run and shown numerically in the second table and visually in a graph.

Run the Buffon's needle experiment with needle lengths \(L \in \{0.3, 0.5, 0.7, 1\}\). In each case, watch the estimate of \(\pi\) as the simulation runs.

Let us analyze the estimation problem more carefully. On each run \(j\) we have an indicator variable \(I_j\), where \(I_j = 1\) if the needle crosses a crack on run \(j\) and \(I_j = 0\) if the needle does not cross a crack on run \(j\). These indicator variables are independent, and identically distributed, since we are assuming independent replications of the experiment. Thus, the sequence forms a Bernoulli trials process.

The number of crack crossings in the first \(n\) runs of the experiment is \[ N_n = \sum_{j=1}^n I_j \] which has the binomial distribution with parameters \(n\) and \(2 L / \pi\).

The mean and variance of \(N_n\) are

• \(\E(N_n) = n \frac{2 L}{\pi}\)
• \(\var(N_n) = n \frac{2 L}{\pi} \left(1 - \frac{2 L}{\pi}\right)\)

With probability 1, \(\frac{N_n}{2 L n} \to \frac{1}{\pi}\) as \(n \to \infty\) and \(\frac{2 L n}{N_n} \to \pi\) as \(n \to \infty\).

These results follow from the strong law of large numbers.

Thus, we have two basic estimators: \(\frac{N_n}{2 L n}\) as an estimator of \(\frac{1}{\pi}\) and \(\frac{2 L n}{N_n}\) as an estimator of \(\pi\). The estimator of \(\frac{1}{\pi}\) has several important statistical properties. First, it is unbiased since the expected value of the estimator is the parameter being estimated:

The estimator of \(\frac{1}{\pi}\) is unbiased : \[ \E \left( \frac{N_n}{2 L n} \right) = \frac{1}{\pi} \]

This follows from the results above for the binomial distribution and properties of expected value.

Since this estimator is unbiased, the variance gives the mean square error: \[ \var \left( \frac{N_n}{2 L n} \right) = \E \left[ \left( \frac{N_n}{2 L n} - \frac{1}{\pi} \right)^2 \right] \]

The mean square error of the estimator of \( \frac{1}{\pi} \) is \[ \var \left( \frac{N_n}{2 L n} \right) = \frac{\pi - 2 L}{2 L n \pi^2} \]

The variance is a decreasing function of the needle length \(L\).

Thus, the estimator of \(\frac{1}{\pi}\) improves as the needle length increases. On the other hand, the estimator of \(\pi\) is biased; it tends to overestimate \(\pi\):

The estimator of \(\pi\) is positively biased: \[ \E \left( \frac{2 L n}{N_n} \right) \ge \pi \]

Use Jensen's inequality.

The estimator of \(\pi\) also tends to improve as the needle length increases. This is not easy to see mathematically. However, you can see it empirically.

In the Buffon's needle experiment, run the simulation 5000 times each with \(L = 0.3\), \(L = 0.5\), \(L = 0.7\), and \(L = 0.9\). Note how well the estimator seems to work in each case.

Finally, we should note that as a practical matter, Buffon's needle experiment is not a very efficient method of approximating \(\pi\). According to Richard Durrett, to estimate \(\pi\) to four decimal places with \(L = \frac{1}{2}\) would require about 100 million tosses!

Run the Buffon's needle experiment until the estimates of \(\pi\) seem to be consistently correct to two decimal places. Note the number of runs required. Try this for needle lengths \(L = 0.3\), \(L = 0.5\), \(L = 0.7\), and \(L = 0.9\) and compare the results.

Show how to simulate the angle \(X\) and distance \(Y\) in Buffon's needle experiment using random numbers.

\(X = \pi U\), \(Y = V\), where \(U\) and \(V\) are random numbers.

Buffon's needle problem is essentially solved by Monte-Carlo integration . In general, Monte-Carlo methods use statistical sampling to approximate the solutions of problems that are difficult to solve analytically. The modern theory of Monte-Carlo methods began with Stanislaw Ulam, who used the methods on problems associated with the development of the hydrogen bomb.

The original needle problem has been extended in many ways, starting with Simon Laplace who considered a floor with rectangular tiles. Indeed, variations on the problem are active research problems even today.

Neil Weiss has pointed out that our computer simulation of Buffon's needle experiment is circular , in the sense the program assumes knowledge of \(\pi\) (you can see this from the simulation result above).

Try to write a computer algorithm for Buffon's needle problem, without assuming the value of \(\pi\) or any other transcendental numbers.

Buffon's What?

This program simulates Buffon's Needle, a real-world experiment for estimating π's value. It's done by taking a large number of needles and dumping them on a wooden floor made of boards as wide as the needles are long. Assuming the needles land in random positions, the fraction of them that end up touching a crack between boards will be about 2/π.

What does this crude physical process have to do with π's value? It acts out a form of Monte Carlo integration. Whether a given needle hits a crack is a matter of trigonometry, so π shows up as one of the integration limits.

A random tangent (boooo...) on Monte Carlo integration

A / [( x 1 - x 0 )( y 1 - y 0 )]

What this has to do with the needles:

Every needle that falls will generate 2 random numbers on landing. y is the distance between the needle's midpoint and the nearest crack (in needle-lengths or floorboard-widths, to keep the math simple). x is the angle the needle makes with that crack:

The needle touches the crack if

y < ½ sin x

which is exactly the condition for a hit in a Monte Carlo integration where f ( x ) = ½ sin x . x can be anywhere between 0 and π. (Allowing negative values of x would be redundant--the only difference between, say, π/2 and -π/2 is which end of the needle hits.) So x 0 = 0, x 1 = π and:

A = 0 ∫ π ½ sin x d x = 1

Meanwhile, since no point on a floorboard is more than half a width from the edge, y must be between y 0 = 0 and y 1 = ½. This is enough to show that the probability of a hit is indeed

hits/needles = 1 / [( x 1 - x 0 )( y 1 - y 0 )] = 1 / [(½)π] = 2/π

OK, but "iterative"?

This is actually the main purpose of the program. It's meant to test one way that Buffon's Needle might be adapted for computer simulation: the program starts with a guess at π's value and tries to refine it through successive runs of the experiment.

Buffon's Needle does not translate well to a computer model. In the real world, the laws of physics distribute x 's values evenly across the interval [0, π) without any help from the experimenter. Simulating this would mean having a random number generator pick numbers in that interval, but to do that it would have to know π already. This defeats the purpose of modeling --deriving a result that wasn't given in the original data--even if it does make some spiffy demos possible.

What if the random number generator were given a wrong value of π for x 's upper bound? Would the estimate derived from the simulation be any closer to the right one? If so, a true computer model of Buffon's Needle is possible--we simply have the program to do another run, feeding the new estimate of π into the generator and getting a still better estimate out. After enough runs the results should converge on π. (Well, not exactly...we're dealing with a random process that only produces rational numbers...but close enough.)

There's just one complication: the program only works if a single iteration actually does give a better value of π (on average) than it started with. As far as I know, this has never been proven. It's certainly fair to expect that this program can improve on an initial guess that's sufficiently wrong: sin x oscillates, so the monstrous x 's that result from a guess of π = 10,000 will behave just like x 's between 0 and the real π (though they won't be quite so evenly distributed). Other than that, I have no idea what (if anything) about the mathematics of the problem would make this program work.

The simulator's performance

But work it certainly seems to. With default settings, it manages to begin generating values around π in less than a dozen trials regardless of whether the initial guess is something reasonable like 3 or absurd like 0.001. The only guess that seems to break the simulation is 0. How close it gets to π is limited by the element of chance in individual trials, but the average for all iterations tends to be correct to 2 decimal places.

I have not experimented much with varying the number of iterations or the number of needles thrown per iteration. Reducing these would probably hurt the accuracy, but I don't know by how much. Feel free to try it.

3.3.1 Buffon's Needle Experiment

Random variables. Any experimental outcome is fully described by the position of the needle on the surface. A convenient depiction of this position is given by two random variables (see Figure 3.17): Y = distance from the center of the needle to the closest of the equidistant parallel lines = angle of the needle, measured with respect to the parallel lines With the position random variables defined in this way, we clearly have 0 Y d/2 and 0 . This choice of random variables is motivated in part by symmetries that can be exploited and in part by the simple probability laws that govern their behavior. Other sets of random variables could be selected, some that would lead to tractable analyses and some that would not. For instance, we could define Y to be the distance from the center of the needle to the next "southern" parallel line (assuming that the lines run east-west). In this case 0 Y d, and the analysis follows very closely the analysis given below. However, we could also define the position of the needle by the (x,y) coordinates of its two end points; this would lead to an unnecessarily complicated analysis. In analyzing an experiment, the efficient selection of a reasonable set of random variables often comes only with modeling experience. Joint sample space. For the position random variables we have selected, the joint (Y, ) sample space corresponds to the rectangle 0 y d/2, 0 (Figure 3.18). Joint probability distribution. To determine the joint probability density function f Y, (y, ) we must interpret the words "at random," describing the throwing mechanism. This is often not an easy thing to do, as the example in the next section will illustrate. In the absence of other information, it is plausible to assume here that the angular position of the needle is uniformly distributed between 0 and , and thus the marginal pdf for the angle is Similarly, it is reasonable to assume that the location of the center of the needle is uniformly distributed, implying that To obtain the joint pdf, f y , (· , ·)it would be "nice" if and Y were independent, for then the joint pdf would simply be the product of the two marginals. Indeed, in this case, there is no reason to assume that knowing the needle's angle would affect one's knowledge about its center position or conversely, and thus the independence assumption can be invoked. Thus, 4. Working in the joint sample space. We are asked for the probability that the needle intersects one of the parallel lines. To answer this question, all we need do is identify the set of points in the joint (Y, ) sample space that corresponds to "intersection of a parallel line" and integrate the joint pdf over that set of points to obtain the desired probability. To do this, we must define "intersection of a parallel line" in terms of the random variables in the sample space. By examining Figure 3.17, it is clear that intersection will occur if "y is sufficiently small for a given angle ." Assuming the situation shown in Figure 3.17, the coordinate of the lower end of the needle is y - (1/2) sin . If this coordinate is negative, intersection will occur. Thus, intersection occurs for all points in the (Y, ) sample space satisfying the inequality y (l/2) sin . Integrating over this set (see Figure 3.19), we obtain the desired probability: A somewhat remarkable property of this result is that it contains a fundamental constant of nature, . If one threw needles many times (and independently) at a lined surface, one could estimate . Exercise 3.4-. Buffon's Needle, Another Way Redo this analysis assuming that the random variable Y is the distance from the center of the needle to the next "southern" parallel line (so that 0 Y d). Exercise 3.5: Buffon's Longer Needle Solve the Buffon needle problem for the case in which the needle is unrestricted in length, (This requires an analysis of the case I > d.)