what is the importance of mathematics in nature essay

Nature by numbers: The hidden beauty of mathematics

L iving with a mathematician this year has made me realise the unsung contribution mathematics makes when it comes to providing us with the reasoning to better appreciate the beauty of nature. I’d always thought fractal symmetry, which cropped up in my physical chemistry lectures, was solely a chemical concept. You can probably imagine my surprise when I realised that this characteristic actually stemmed from mathematics. It came as an even greater shock to discover that many natural phenomena are, in fact, fractal to some degree. The Fibonacci sequence, which you may think exists only in the pages of a Dan Brown novel, is also visible in some of nature’s most exquisite structures. So, just how many of us are aware of the way in which mathematics provides us with the reasoning to be able to praise the intrinsic beauty of nature? This is exactly what I hope to achieve in this article; to show you how mathematics, something some of us may have dreaded at school, actually explains a lot of the things we see around us.

Fractal symmetry is when the same pattern is seen at increasingly small scales. In fractal symmetry, you find the same pattern within the pattern, which is why this can also be referred to as self-similarity. The best example to think of is a tree. The trunk of a tree separates into branches which then separate into smaller branches and then twigs, and these get smaller and smaller. In this way, we see a repetition. Another example is the Romanesco broccoli, but my favourite would have to be the Lotus effect. The Lotus leaves have a rough surface with micro- and nano-structures including waxy crystals that contribute to making the surface superhydrophobic. This means that any water droplets on the lotus leaves are strongly repelled and slide off the surface. While doing so, they take up the dust particles from the leaves in order to reduce the surface tension, resulting in the cleaning of the lotus leaves. This is an example of self-cleaning in nature and it is the fractal symmetry of the waxy crystals on the surface of the leaves that provides the enhanced hydrophobicity which makes this possible.

Fractal symmetry is when the same pattern is seen at increasingly small scales. In fractal symmetry, you find the same pattern within the pattern, which is why this can also be referred to as self-similarity

Another type of symmetry I wish to discuss is the so-called wallpaper symmetry. This is the mathematical classification of a two-dimensional repetitive pattern inspired by honeycomb structures. Besides often being seen in architecture and other arts such as textiles, this structure has found great use in the field of chemical catalysis. One of the finest examples of the use of catalysis is in catalytic converters used to turn pollutant gases such as nitrogen oxides and carbon monoxides into nitrogen dioxide and carbon dioxide gases, which are safer alternatives. The support for the precious rhodium or platinum metal catalysts used is cordierite monolith. The metal is dispersed on the honeycomb structure of the support which provides a larger surface area to optimise the flow of gases over the catalyst. This is a fine example of symmetry observed in nature that has now been employed on a large industrial scale and is something used by many of us every day.

Fractal and wallpaper symmetry are the two types I wanted to discuss. However, this article would be incomplete without a nod to the spirals that are too often seen in nature. Some of these spirals arise due to the golden ratio of 1.618[…] which is the most irrational number we can get. Put simply, it is the furthest away we can be from a fraction. In this way, the golden ratio gives the best spiral with no gaps. Hence, flower petals and pinecones are guided by the golden ratio, which is related to the Fibonacci sequence. In the Fibonacci sequence, each number is the sum of the two numbers preceding it. What we find is that if we take the ratio of any two numbers from the Fibonacci sequence, we get values very close to the golden ratio. In nature, the flowers and the shells are not genetically, or in any other way, programmed to abide by the mathematics of the Fibonacci sequence. This is purely a result of evolutionary design. Petals and seeds find that the golden ratio offers the best packing with minimum gaps. I find it absolutely amazing that a series of numbers on a piece of paper can explain why many elements in nature have chosen to adopt this particular configuration.

This article would be incomplete without a nod to the spirals that are too often seen in nature. Some of these spirals arise due to the golden ratio of 1.618[…] which is the most irrational number we can get

In addition to mathematics, you could not have avoided noticing the not-so-subtle mention of chemistry in this article. As I researched more into maths, I could easily find myself making connections with chemistry and much of the material I have studied to date. Thinking back to one of the conversations I’ve had with my flatmates in the kitchen, it’s clear that mathematics provides the key to untie the knots in many fields both within and outside STEM. As a chemist, I certainly see how fundamental a role mathematics plays. In this article, I hope I have enabled you to at least begin to appreciate just how much a bunch of numbers can explain to us about the universe.

The Power of Mathematics: Unveiling its Influence on Nature and Phenomena

Introduction.

*minimum deadline

Cite this Essay

To export a reference to this article please select a referencing style below

Space Exploration
Stephen Hawking

Related Essays

Need writing help?

You can always rely on us no matter what type of paper you need

*No hidden charges

100% Unique Essays

Absolutely Confidential

Money Back Guarantee

By clicking “Send Essay”, you agree to our Terms of service and Privacy statement. We will occasionally send you account related emails

You can also get a UNIQUE essay on this or any other topic

Thank you! We’ll contact you as soon as possible.

Math Careers

Search form

MAA Centennial
Spotlight: Archives of American Mathematics
MAA Officers
MAA to the Power of New
Council and Committees
MAA Code of Conduct
Policy on Conflict of Interest
Statement about Conflict of Interest
Recording or Broadcasting of MAA Events
Policy for Establishing Endowments and Funds
Avoiding Implicit Bias
Copyright Agreement
Principal Investigator's Manual
Planned Giving
The Icosahedron Society
Our Partners
Advertise with MAA
Employment Opportunities
Staff Directory
2022 Impact Report
In Memoriam
Membership Categories
Become a Member
Membership Renewal
MERCER Insurance
MAA Member Directories
New Member Benefits
The American Mathematical Monthly
Mathematics Magazine
The College Mathematics Journal
How to Cite
Communications in Visual Mathematics
About Convergence
What's in Convergence?
Convergence Articles
Mathematical Treasures
Portrait Gallery
Paul R. Halmos Photograph Collection
Other Images
Critics Corner
Problems from Another Time
Conference Calendar
Guidelines for Convergence Authors
Math Horizons
Submissions to MAA Periodicals
Guide for Referees
Scatterplot
Math Values
MAA Book Series
MAA Press (an imprint of the AMS)
MAA Library Recommendations
Additional Sources for Math Book Reviews
About MAA Reviews
Mathematical Communication
Information for Libraries
Author Resources
MAA MathFest
Proposal and Abstract Deadlines
MAA Policies
Invited Paper Session Proposals
Contributed Paper Session Proposals
Panel, Poster, Town Hall, and Workshop Proposals
Minicourse Proposals
MAA Section Meetings
Virtual Programming
Joint Mathematics Meetings
Calendar of Events
MathFest Programs Archive
MathFest Abstract Archive
Historical Speakers
Information for School Administrators
Information for Students and Parents
Registration
Getting Started with the AMC
AMC Policies
AMC Administration Policies
Important AMC Dates
Competition Locations
Invitational Competitions
Putnam Competition Archive
AMC International
Curriculum Inspirations
Sliffe Award
MAA K-12 Benefits
Mailing List Requests
Statistics & Awards
Submit an NSF Proposal with MAA
MAA Distinguished Lecture Series
Common Vision
CUPM Curriculum Guide
Instructional Practices Guide
Möbius MAA Placement Test Suite
META Math Webinar May 2020
Progress through Calculus
Survey and Reports
"Camp" of Mathematical Queeries
DMEG Awardees
National Research Experience for Undergraduates Program (NREUP)
Neff Outreach Fund Awardees
Tensor SUMMA Grants
Tensor Women & Mathematics Grants
Grantee Highlight Stories
"Best Practices" Statements
CoMInDS Summer Workshop 2023
MAA Travel Grants for Project ACCCESS
2024 Summer Workshops
Minority Serving Institutions Leadership Summit
Previous Workshops
Frequently Asked Questions
Course Resources
Industrial Math Case Studies
Participating Faculty
2020 PIC Math Student Showcase
Previous PIC Math Workshops on Data Science
Dates and Locations
Past Programs
Leadership Team
Support Project NExT
Section NExT
Section Officers Meeting History
Preparations for Section Meetings
Bylaws Template
Editor Lectures Program
MAA Section Lecturer Series
Officer Election Support
Section Awards
Section Liaison Programs
Section Visitors Program
Expense Reimbursement
Guidelines for Bylaw Revisions
Guidelines for Local Arrangement Chair and/or Committee
Guidelines for Section Webmasters
MAA Logo Guidelines
MAA Section Email Policy
Section Newsletter Guidelines
Statement on Federal Tax ID and 501(c)3 Status
Communication Support
Guidelines for the Section Secretary and Treasurer
Legal & Liability Support for Section Officers
Section Marketing Services
Section in a Box
Subventions and Section Finances
Web Services
Joining a SIGMAA
Forming a SIGMAA
History of SIGMAA
SIGMAA Officer Handbook
MAA Connect
Meetings and Conferences for Students
Opportunities to Present
Information and Resources
MAA Undergraduate Student Poster Session
Undergraduate Research Resources
MathFest Student Paper Sessions
Research Experiences for Undergraduates
Student Poster Session FAQs
High School
A Graduate School Primer
Reading List
Student Chapters
Awards Booklets
Carl B. Allendoerfer Awards
Regulations Governing the Association's Award of The Chauvenet Prize
Trevor Evans Awards
Paul R. Halmos - Lester R. Ford Awards
Merten M. Hasse Prize
George Pólya Awards
David P. Robbins Prize
Beckenbach Book Prize
Euler Book Prize
Daniel Solow Author’s Award
Henry L. Alder Award
Deborah and Franklin Tepper Haimo Award
Certificate of Merit
Gung and Hu Distinguished Service
JPBM Communications Award
Meritorious Service
MAA Award for Inclusivity
T. Christine Stevens Award
Dolciani Award Guidelines
Morgan Prize Information
Selden Award Eligibility and Guidelines for Nomination
Selden Award Nomination Form
AMS-MAA-SIAM Gerald and Judith Porter Public Lecture
Etta Zuber Falconer
Hedrick Lectures
James R. C. Leitzel Lecture
Pólya Lecturer Information
Putnam Competition Individual and Team Winners
D. E. Shaw Group AMC 8 Awards & Certificates
Maryam Mirzakhani AMC 10 A Awards & Certificates
Two Sigma AMC 10 B Awards & Certificates
Jane Street AMC 12 A Awards & Certificates
Akamai AMC 12 B Awards & Certificates
High School Teachers
MAA Social Media

V. I. Arnold

The Basic Library List Committee suggests that undergraduate mathematics libraries consider this book for acquisition.

Table of Contents

This is a collection of 39 essays from the distinguished mathematician Vladimir Arnold. He was a man of very strong opinions. One of these is especially pertinent for this collection:

Mathematics is a part of physics. Physics is an experimental science, a part of natural science. Mathematics is the part of physics where experiments are cheap.

The book’s editor notes that from the age of eleven Arnold was a member of the “Children’s Learned Society”, which had been organized by A. A. Lyapunov and run at his home. The curriculum included mathematics and physics with a bit of chemistry and biology. The current book seems to have been motivated by these early experiences.

The essays are short — none longer than about six pages — and address topics mostly in mathematics and physics. The levels of sophistication and difficulty vary widely. Some topics would be accessible to high school students with a little bit of algebra and geometry; others might challenge even specialists. In the first category is an essay on the eccentricity of the orbit of Mars. It is implicitly a lesson on intelligent estimation. In the second category is a piece about adiabatic invariants.

Arnold’s introduction includes the comment: “Examples teach no less than rules, and errors, more than correct but abstruse proofs.” It is a wonderful teaching point that is amplified by at least a few unintentional errors in the text. One, noted by the editor, is about the forward motion of a bicycle. (If you attach a string to lower pedal of a bicycle at rest and pull straight back, does the bicycle move forwards or backwards?) Another occurs in an essay about the rainbow, and rather oddly attributes the blueness of the sky to a Moiré effect.

This is a wonderful book for browsing, for anyone drawn to physical applications of mathematics or to Arnold himself and the breadth of his interests. To sample some of his wizardly work, look at the essay on the maximum deviation of a light beam through a water drop and the following essay on the rainbow.

Bill Satzer ( [email protected] ) is a senior intellectual property scientist at 3M Company, having previously been a lab manager at 3M for composites and electromagnetic materials. His training is in dynamical systems and particularly celestial mechanics; his current interests are broadly in applied mathematics and the teaching of mathematics.

See the table of contents in pdf format .

Dummy View - NOT TO BE DELETED

what is the importance of mathematics in nature essay

MAA Publications

Periodicals
MAA History
Policies and Procedures
Support MAA
Member Discount Programs
Propose a Session
MathFest Archive
Putnam Competition
AMC Resources
Curriculum Resources
Outreach Initiatives
Professional Development
Communities

Connect with MAA

Mathematical Association of America P: (800) 331-1622 F: (240) 396-5647 Email: [email protected]

Terms of Use
Privacy Policy
Mobile Version

Mathematics and the environment

Credit: Tetra Images Photography/Shutterstock

Some people claim that the discoveries made by scientists contribute to the destruction of the natural environment. Professor Louis Gross at the University of Tennessee shows that the case can equally be made for the opposite. He is a mathematical ecologist, applying advanced mathematics to the problems of managing the natural environment to maximise the benefits to the whole natural system. The pressures of human life have an effect on the rest of nature and by understanding how the relationships work, everyone and everything might get some of what they want.

It turns out that these problems are not trivial mathematically. The flow pattern of a river might have a linear relationship with the rainfall in a particular place, but what happens when the river bursts its banks? Or if it rains after a period of drought? And how do you know what the rainfall is going to be anyway?

Not only are many natural processes essentially stochastic they also require nonlinear algebra to describe them. Getting meaningful results is a huge mathematical and computational exercise. This is why Gross, like many scientists from other, more conventional fields, has turned his attention to the mathematics of the natural world – it has some of the most interesting mathematical problems. Mathematical biology has achieved a high profile through cell biology and genomics, but at the scale of the whole ecosystem it is still in its emerging stage and the field has many opportunities to do new things.

Professor Alan Hastings, from the Department of Environmental Science and Policy at the University of California, Davis, has known Gross since graduate school where they had the same supervisor. He preceded Gross as President of the Society for Mathematical Biology. He says: ‘He is very outgoing and enthusiastic. He has done a tremendous amount of organisational work and is very active in doing things which have a world wide impact.

‘His major contributions have been in formulating and leading in the development of computer models for understanding the dynamics of ecosystems. He has been very involved in issues around training in mathematical biology. He is certainly one of the earlier people in this field.’

Lou Gross was born in Philadelphia. His father was an electrical engineer and his mother a bookkeeper. His interest in science began on a planetarium visit in the second grade. This grew into a fascination with radio-astronomy which in turn drove him to study hard at mathematics. This did not make him into a nerd – he was also a very keen boy scout and sports runner.

He went to Drexel University in Philadelphia, which offered a cooperative education programme allowing students to work for six months and then study for six months. For six months a year he was paid to work at the National Radio Astronomy Observatory in Charlottesville, and for the rest of the year he studied mathematics.

He was not just involved in lowly work but was encouraged to work on new ideas. He spent a lot of time developing computer programmes to control the interferometers that were being developed at the time. He had access to an IBM 360 mainframe with all of 360k of main memory, which taught him a lot about writing efficient programmes.

Gross had already become interested in mathematical biology before he entered the graduate programme at Cornell. It was an emerging field at the time, although some aspects had been around for many years, such as population genetics. He had taken a course at Drexel on the mathematics of human biology with a focus on demography and had become enthralled by the subject. He liked the stochastic mathematics and the real world possibilities of applying mathematics to biology.

He joined a small applied mathematics group at Cornell and did some work on neural network models of the human brain. He did not think that was going to go anywhere very soon, but at the same time he started taking a course in ecology from Simon Levin. He also met his other great mentor Brian Chabot, who was a plant physiology ecologist.

He says: ‘I realised that there had not been very much work done on photosynthesis. It was an opportunity for me to do something that I had not done before, which is laboratory work. As part of my dissertation I wrote a paper which was published on the dynamics of photosynthesis. I looked at how carbon uptake changes in response to changes in light. There are still many opportunities in biology that are completely new.’

After gaining his PhD he was certain about what he wanted to do – and made his first, and so far only, career move. He says: ‘I immediately accepted a position at the University of Tennessee because of my colleague Thomas Hallam, who had been hired here specifically to build a programme in mathematical biology with an emphasis on ecology. There were very few other places that were so forward thinking and had recognised the importance of the subject. I was appointed to the mathematics department, but I also held a position in ecology, although that was not a department at the time. I continued my work on photosynthesis here, before being drawn into other things. Even now, the strong programmes in the field do not have large groups working on them, and yet that is enough. Computational biology has grown as a field, but this tends to mean things below the organism scale – like genomics.’

Gross accepts that the growth of mathematics in fields like genomics and cell biology has gained a higher public profile than his work in recent years, because people feel that it has a direct impact on human health. His work has concentrated on a much larger scale, but he believes it can also have a direct impact on human life.

He says: ‘My major research project over the past two decades has been on Everglades restoration. This is an example of a large piece of real estate in which the driving force for the natural systems and social systems is the water. Where the water is makes a big difference to where the people are and where they are not, as well as the organisms and the responses of the whole system. It is a tremendously interlinked system where the human systems have an impact on the natural systems.

‘Unfortunately there are a very large number of stakeholders who have different views as to how the system might be appropriately managed. We use computational models rather than mathematical models, because it’s extremely difficult to write down any set of equations that are complicated enough to capture the essence of the system and still be able to say anything useful. These models can determine the implications of different human actions. What we say is, if you manage the system this way, how does that impact the system of the Everglades and we have come up with a hydrological model look at the implications of different plans on the biota.

‘One of the things that we have learned from theory in ecology is the scales in which you are interested and the scales in which they respond are tremendously important. In the Everglades, the spatial scales are rather broad, so what is happening in one part of the system may be very much decoupled from other parts of the system, unless something like the water is coupling the system. Unfortunately, the water is coupling the system so you cannot take a simple average in the way that you would with a linear process and expect it to work out. That is one of the things that we have tried to deal with in the Everglades models. What happens in one part of space should be discernable from what is happening in another part of space.

We have always been asked for one number that says one management plan is better than another management plan and we have always refused to do it. We have come down to producing maps that display how natural systems work with time series. We developed a methodology called relative assessment with two maps that represent different management schemes and show the differences between them. You can then do a time series of these maps and people can pick out the nonlinearities and see how certain populations have crashed in response to a change in the water.’

One project Gross’s group has been examining is saving the Florida panther, which is related to the cougar, and was on the verge of extinction with a population below 30 in 1995. The plan was to import female cougars from Texas who had once interbred with Florida Panthers; now the population has grown to 100. The group is working on population augmentation model to help plan such projects.

‘These models were not available at the time and we are now working on them. It was an example of a relatively simple ecological idea, but the mathematics had not been worked out. It was basically a problem in optimal control – a long standing field in mathematics – which has differential equations with a control parameter that you can modify to maximise or minimise something under certain constraints. This is a relatively new field in biological systems, but it has applications in other areas.

‘What we are trying to do with the Everglades is work out what to do, where to do it and when and how to assess what you have done. This is highly computational and involves a lot of intensive parallel computing, because when you do something in one place it affects what happens in another place. You have a huge control space with sometimes millions of control variables.’

He says a lot of ecological models can also be used in other fields, such as infection control. In many cases, he says, there are ‘rules of thumb’ that people have used for many years to make decisions on managing natural systems. The mathematical models can sometimes come up with alternative strategies, which can be shown to be more effective under certain circumstances. Gross has discovered that many issues in managing the environment, from controlling the activity of hunters to keep bears away from human settlements to controlling forest fires, are actually very interesting mathematical problems, often involving stochastic process. In many ways there are parallels with the ways that advanced mathematics has become an important part of the creation of investment strategies in the financial markets.

Gross has been at the University of Tennessee in Knoxville since 1979 and has no inclination to do the common academic shuffle between institutions to get resources, greater salary or prestige. He was brought in by a university management which, in many ways, was ahead of the game in encouraging interdisciplinary research activities and as a result he has been given a long leash. Of course his department has not been expensive to run, with many millions of dollars being brought in through research grants as the field of environmental management has acquired a higher political profile.

He says: ‘What has been good about staying here is that we have been able to build one of the best programmes in the world in mathematical biology. We have done this in a collaborative way. The Institute for Environmental Modelling has allowed us to work with a wide variety of people from different specialities. There are few other universities where it would be so easy to set up an interdisciplinary research institute.

‘Modern biology is very interdisciplinary and, in order to train the next generation of biologists, we will need to inculcate them with a lot of other specialities. One of the challenges is how to modify the undergraduate curricula so that they see other subjects. One way to do this is with electives, the other is to have truly interdisciplinary courses.’

So how was he able to persuade his university to pioneer this approach? ‘Well, it didn’t cost them very much. We got some stationery and we were up and running,’ says Gross. Since then his institute has brought in some $15m in external funding. One well-known outputs from his research is the SADA software package which is used for planning site remediation all over the world. Its development is funded by the Nuclear Regulatory Commission.

Another reason for his decision not to move is the ‘academic two body problem’. His wife is also an academic in poetry and although he has been courted by many other institutions he has not been able to tackle the double hire issue. He is also very happy where he is.

In the future he is hopeful that the growing profile of mathematical biology at the cell level will eventually spread to his work at a macroscopic level. He says that one of the problems is that many of the academic meetings have become quite specialised. Mathematical papers are presented at meetings about a particular area of biology and people in that field are unwilling at the moment to go to meetings where all they talk about is mathematical biology, but across many fields.

Gross has served as President of the Society for Mathematical Biology and he hopes that in the future this will emerge as more of a field in its own right. He says: ‘There are so many things that you can learn from how people in other areas of biology are using mathematical methods. There are many routes to how the field is advanced. Some of these developments will occur in mathematics departments and others will happen in biological science research. For example, there is a growing field of agent-based modelling, which has so far seen few applications outside ecology. They can be equally applied to many other fields and the computational tools are becoming available and people without a huge amount of coding experience can do something new.’

Much of Gross’s work has been around parallel processing simply because in ecology you have to do it because of the synchrony of biological systems. Gross believes that the same approach can be used in human biology by studying ‘whole human’ responses.

Gross has developed a number of interests outside of his university work. Most notably he is the sound engineer for a local theatre in Knoxville. He has published articles in journals about designing theatre sound systems.

This stems from a deep interest in what might be called folk music, but his tastes are very broad. Another reason to stay put in Tennessee?

Lou Gross CV

1974 BS in Mathematics with Honours, Drexel University

1979 PhD in Applied Mathematics, Cornell University.

Professional appointments

1979-1985: Assistant Professor, Department of Mathematics and Graduate Program in Ecology, University of Tennessee, Knoxville.

1985-1992: Associate Professor, Department of Mathematics, University of Tennessee, Knoxville,

1992-1997: Professor, Department of Mathematics, University of Tennessee, Knoxville,

1997-present: Professor, Departments of Ecology and Evolutionary Biology and Mathematics University of Tennessee, Knoxville,

1998-present: Director, The Institute for Environmental Modelling, University of Tennessee, Knoxville,

Essay on Importance of Mathematics in Our Daily Life

Students are often asked to write an essay on Importance of Mathematics in Our Daily Life in their schools and colleges. And if you’re also looking for the same, we have created 100-word, 250-word, and 500-word essays on the topic.

Let’s take a look…

100 Words Essay on Importance of Mathematics in Our Daily Life

Introduction.

Mathematics is a crucial part of everyday life. It helps us make sense of the world around us and solve practical problems.

Mathematics in Daily Tasks

From shopping to cooking, we use math. It helps us calculate costs, quantities, and time.

Mathematics in Professions

In professions like engineering, computer science, and finance, math is indispensable.

Mathematics in Decision Making

Math helps us make informed decisions by analyzing data and predicting outcomes.

Thus, math plays a vital role in our daily lives, making it an essential subject to learn.

250 Words Essay on Importance of Mathematics in Our Daily Life

The pervasive presence of mathematics.

Mathematics, often perceived as a complex and abstract discipline, is in fact an integral part of our everyday lives. It forms the foundation for many of the decisions we make and the actions we perform daily, from managing finances to navigating directions.

A Tool for Logical Reasoning

Mathematics fosters logical reasoning and problem-solving skills. It cultivates an analytical mindset, enabling us to break down complex problems into simpler, manageable parts. This approach is not just confined to mathematical problems but extends to various real-life situations, thereby honing our decision-making abilities.

Mathematics in Technological Advancements

The rapid progress in technology, which has become an inseparable part of our lives, is deeply rooted in mathematical principles. Algorithms, which form the basis of computing, are mathematical models. The internet, smartphones, GPS, and even AI owe their existence to mathematical concepts.

Financial Management and Mathematics

Managing personal finances, a critical life skill, is essentially a mathematical exercise. Budgeting, calculating interest, understanding the implications of loans and mortgages, or even evaluating investment options, all require a good grasp of mathematics.

Mathematics and Scientific Understanding

Mathematics is the language of science. It helps us quantitatively understand and describe the physical world around us, from the trajectory of planets to the behavior of subatomic particles.

In conclusion, mathematics is a vital part of our daily lives. It is not just a subject to be studied in school, but a tool for understanding, navigating, and shaping the world around us. Its importance cannot be overstated, as it is the foundation of critical thinking, technological progress, financial management, and scientific understanding.

500 Words Essay on Importance of Mathematics in Our Daily Life

Mathematics, often perceived as a complex and abstract subject, is in fact deeply intertwined with our daily lives. It is the foundation of numerous activities we engage in, from basic tasks such as shopping and cooking to more complex ones like planning finances or solving problems.

The Ubiquity of Mathematics

Mathematics is everywhere. It is used in our everyday activities, often without our conscious realization. When we shop, we use mathematics to calculate prices, discounts, and taxes. When we cook, we use it to measure ingredients. When we travel, we use it to calculate distances, time, and fuel consumption. Even in our leisure activities such as playing games or music, mathematics plays a crucial role in understanding patterns, probabilities, and rhythms.

Mathematics in the Professional Sphere

In the professional world, the significance of mathematics is even more pronounced. Engineers use mathematical principles to design and build infrastructure. Economists use it to predict market trends. Computer scientists use algorithms and data structures, which are fundamentally mathematical in nature, to design efficient software. Even in fields that are traditionally considered non-mathematical, such as literature and arts, mathematical concepts such as symmetry, geometry, and proportion play a key role in creating aesthetic appeal.

Mathematics and Problem-Solving

Mathematics also enhances our problem-solving skills. It teaches us to approach problems logically and systematically. It encourages us to break down complex problems into simpler parts, solve them individually, and combine the solutions to solve the original problem. This skill is not just applicable to mathematical problems but to any problem we encounter in life.

Mathematics and Critical Thinking

Furthermore, mathematics fosters critical thinking. It trains us to question assumptions, identify patterns, and draw conclusions based on evidence. It also teaches us to understand the limitations of our solutions and consider alternative approaches. These are valuable skills that can be applied in various aspects of life, from making informed decisions to evaluating the credibility of information.

Mathematics and the Digital Age

In the digital age, the importance of mathematics has grown exponentially. It is the backbone of modern technologies such as artificial intelligence, machine learning, data analysis, cryptography, and quantum computing. Understanding mathematics is essential to navigate and thrive in this digital world.

In conclusion, mathematics is not just a subject we learn in school. It is a powerful tool that helps us understand and navigate the world around us. It enhances our problem-solving and critical thinking skills, and it opens up a world of opportunities in the professional sphere. Therefore, it is essential that we appreciate the importance of mathematics in our daily lives, and strive to improve our mathematical literacy.

That’s it! I hope the essay helped you.

If you’re looking for more, here are essays on other interesting topics:

Essay on Importance of Electricity in Our Life
Essay on My Favourite Season Spring
Essay on The Power of Social Media

Apart from these, you can look at all the essays by clicking here .

Happy studying!

Essay: The Relationship between Math and Nature

ESSAY SAMPLES , Essays on Education

Sample Essay

Mathematics is one of the most fundamental of all the sciences governing our universe. Imagine our own world without it- if we didn’t know about addition and subtraction and the various calculations, none of the worlds would have been the way it is. It the mathematics that has made mankind learn so much about the universe, ocean depths, earthquake intensities etc. Here an important question arises; is math essentially a part of nature or was it developed to actually understand and interpret nature?

Diverse opinions exist in this regard. Some believe math was developed by man intentionally with the purpose of understanding this giant network laid by god. The reason for them to think this way is if math was part of nature, then man would have been born with a natural understanding for it but man instead, has to take classes and think and learn math.

Though math does help us in measuring the out and about nature, yet it is one of the most unspecific ways of actually measuring nature. This is because other sciences like physics and chemistry measure and study about the actual components of our universe. Physics can tell us which force is acting where and why. Chemistry can tell us about the various chemical reactions occurring throughout our universe and their consequences. Math, on the other hand, is merely a number game. It only helps to measure and estimate. Hence it is a generic science applicable to all other sciences and that’s what the magic is math is.

Thank you for visiting Essaydemon.com and viewing our articles and sample papers. Kindly be informed that all these articles and sample papers are for marketing purposes only. The sole purpose of these articles and sample papers is just to provide our customers with an idea about our services before they place an order. Kindly visit our order/inquiry page for further assistance.

Kindly order custom made Essays, Term Papers, Research Papers, Thesis, Dissertation, Assignment, Book Reports, Reviews, Presentations, Projects, Case Studies, Coursework, Homework, Creative Writing, Critical Thinking, on the topic by clicking on the order page.

Sample Essay Data redundancy happens when an organization stores the same type of information in…

Math can be a very difficult subject for some students as it consists of complex…

Sample Essay 5 works cited Length: 1433 words Abstract: Shakespeare talks about the relationships in…

What Students Are Saying About the Value of Math

We asked teenagers: Do you see the point in learning math? The answer from many was “yes.”

By The Learning Network

“Mathematics, I now see, is important because it expands the world,” Alec Wilkinson writes in a recent guest essay . “It is a point of entry into larger concerns. It teaches reverence. It insists one be receptive to wonder. It requires that a person pay close attention.”

In our writing prompt “ Do You See the Point in Learning Math? ” we wanted to know if students agreed. Basic arithmetic, sure, but is there value in learning higher-level math, such as algebra, geometry and calculus? Do we appreciate math enough?

The answer from many students — those who love and those who “detest” the subject alike — was yes. Of course math helps us balance checkbooks and work up budgets, they said, but it also helps us learn how to follow a formula, appreciate music, draw, shoot three-pointers and even skateboard. It gives us different perspectives, helps us organize our chaotic thoughts, makes us more creative, and shows us how to think rationally.

Not all were convinced that young people should have to take higher-level math classes all through high school, but, as one student said, “I can see myself understanding even more how important it is and appreciating it more as I get older.”

Thank you to all the teenagers who joined the conversation on our writing prompts this week, including students from Bentonville West High School in Centerton, Ark, ; Harvard-Westlake School in Los Angeles ; and North High School in North St. Paul, Minn.

Please note: Student comments have been lightly edited for length, but otherwise appear as they were originally submitted.

“Math is a valuable tool and function of the world.”

As a musician, math is intrinsically related to my passion. As a sailor, math is intertwined with the workings of my boat. As a human, math is the building block for all that functions. When I was a child, I could very much relate to wanting a reason behind math. I soon learned that math IS the reason behind all of the world’s workings. Besides the benefits that math provides to one’s intellect, it becomes obvious later in life that math is a valuable tool and function of the world. In music for example, “adolescent mathematics” are used to portray functions of audio engineering. For example, phase shifting a sine wave to better project sound or understanding waves emitted by electricity and how they affect audio signals. To better understand music, math is a recurring pattern of intervals between generating pitches that are all mathematically related. The frets on a guitar are measured precisely to provide intervals based on a tuning system surrounding 440Hz, which is the mathematically calculated middle of the pitches humans can perceive and a string can effectively generate. The difference between intervals in making a chord are not all uniform, so guitar frets are placed in a way where all chords can sound equally consonant and not favor any chord. The power of mathematics! I am fascinated by the way that math creeps its way into all that I do, despite my plentiful efforts to keep it at a safe distance …

— Renan, Miami Country Day School

“Math isn’t about taking derivatives or solving for x, it’s about having the skills to do so and putting them to use elsewhere in life.”

I believe learning mathematics is both crucial to the learning and development of 21st century students and yet also not to be imposed upon learners too heavily. Aside from the rise in career opportunity in fields centered around mathematics, the skills gained while learning math are able to be translated to many facets of life after a student’s education. Learning mathematics develops problem solving skills which combine logic and reasoning in students as they grow. The average calculus student may complain of learning how to take derivatives, arguing that they will never have to use this after high school, and in that, they may be right. Many students in these math classes will become writers, musicians, or historians and may never take a derivative in their life after high school, and thus deem the skill to do so useless. However, learning mathematics isn’t about taking derivatives or solving for x, it’s about having the skills to do so and putting them to use elsewhere in life. A student who excels at calculus may never use it again, but with the skills of creativity and rational thinking presented by this course, learning mathematics will have had a profound effect on their life.

— Cam, Glenbard West

“Just stop and consider your hobbies and pastimes … all of it needs math.”

Math is timing, it’s logic, it’s precision, it’s structure, and it’s the way most of the physical world works. I love math — especially algebra and geometry — as it all follows a formula, and if you set it up just right, you can create almost anything you want in at least two different ways. Just stop and consider your hobbies and pastimes. You could be into skateboarding, basketball, or skiing. You could be like me, and sit at home for hours on end grinding out solves on a Rubik’s cube. Or you could be into sketching. Did you know that a proper drawing of the human face places the eyes exactly halfway down from the top of the head? All of it needs math. Author Alec Wilkinson, when sharing his high school doubting view on mathematics, laments “If I had understood how deeply mathematics is embedded in the world …” You can’t draw a face without proportions. You can’t stop with your skis at just any angle. You can’t get three points without shooting at least 22 feet away from the basket, and get this: you can’t even ride a skateboard if you can’t create four congruent wheels to put on it.

— Marshall, Union High School, Vancouver, WA

“Math gives us a different perspective on everyday activities.”

Even though the question “why do we even do math?” is asked all the time, there is a deeper meaning to the values it shares. Math gives us a different perspective on everyday activities, even if those activities in our routine have absolutely nothing to do with mathematical concepts itself. Geometry, for instance, allows us to think on a different level than simply achieving accuracy maintains. It trains our mind to look at something from various viewpoints as well as teaching us to think before acting and organizing chaotic thoughts. The build up of learning math can allow someone to mature beyond the point where if they didn’t learn math and thought through everything. It paves a way where we develop certain characteristics and traits that are favorable when assisting someone with difficult tasks in the future.

— Linden, Harvard-Westlake High School, CA

“Math teaches us how to think.”

As explained in the article, math is all around us. Shapes, numbers, statistics, you can find math in almost anything and everything. But is it important for all students to learn? I would say so. Math in elementary school years is very important because it teaches how to do simple calculations that can be used in your everyday life; however middle and high school math isn’t used as directly. Math teaches us how to think. It’s far different from any other subject in school, and truly understanding it can be very rewarding. There are also many career paths that are based around math, such as engineering, statistics, or computer programming, for example. These careers are all crucial for society to function, and many pay well. Without a solid background in math, these careers wouldn’t be possible. While math is a very important subject, I also feel it should become optional at some point, perhaps part way through high school. Upper level math classes often lose their educational value if the student isn’t genuinely interested in learning it. I would encourage all students to learn math, but not require it.

— Grey, Cary High School

“Math is a valuable tool for everyone to learn, but students need better influences to show them why it’s useful.”

Although I loved math as a kid, as I got older it felt more like a chore; all the kids would say “when am I ever going to use this in real life?” and even I, who had loved math, couldn’t figure out how it benefits me either. This was until I started asking my dad for help with my homework. He would go on and on about how he used the math I was learning everyday at work and even started giving me examples of when and where I could use it, which changed my perspective completely. Ultimately, I believe that math is a valuable tool for everyone to learn, but students need better influences to show them why it’s useful and where they can use it outside of class.

— Lilly, Union High School

“At the roots of math, it teaches people how to follow a process.”

I do believe that the math outside of arithmetic, percentages, and fractions are the only math skills truly needed for everyone, with all other concepts being only used for certain careers. However, at the same time, I can’t help but want to still learn it. I believe that at the roots of math, it teaches people how to follow a process. All mathematics is about following a formula and then getting the result of it as accurately as possible. It teaches us that in order to get the results needed, all the work must be put and no shortcuts or guesses can be made. Every equation, number, and symbol in math all interconnect with each other, to create formulas that if followed correctly gives us the answer needed. Everything is essential to getting the results needed, and skipping a step will lead to a wrong answer. Although I do understand why many would see no reason to learn math outside of arithmetic, I also see lessons of work ethics and understanding the process that can be applied to many real world scenarios.

— Takuma, Irvine High School

“I see now that math not only works through logic but also creativity.”

A story that will never finish resembling the universe constantly expanding, this is what math is. I detest math, but I love a never-ending tale of mystery and suspense. If we were to see math as an adventure it would make it more enjoyable. I have often had a closed mindset on math, however, viewing it from this perspective, I find it much more appealing. Teachers urge students to try on math and though it seems daunting and useless, once you get to higher math it is still important. I see now that math not only works through logic but also creativity and as the author emphasizes, it is “a fundamental part of the world’s design.” This view on math will help students succeed and have a more open mindset toward math. How is this never-ending story of suspense going to affect YOU?

— Audrey, Vancouver, WA union high school

“In some word problems, I encounter problems that thoroughly interest me.”

I believe math is a crucial thing to learn as you grow up. Math is easily my favorite subject and I wish more people would share my enthusiasm. As Alec Wilkinson writes, “Mathematics, I now see, is important because it expands the world.” I have always enjoyed math, but until the past year, I have not seen a point in higher-level math. In some of the word problems I deal with in these classes, I encounter problems that thoroughly interest me. The problems that I am working on in math involve the speed of a plane being affected by wind. I know this is not riveting to everyone, but I thoroughly wonder about things like this on a daily basis. The type of math used in the plane problems is similar to what Alec is learning — trigonometry. It may not serve the most use to me now, but I believe a thorough understanding of the world is a big part of living a meaningful life.

— Rehan, Cary High School

“Without high school classes, fewer people get that spark of wonder about math.”

I think that math should be required through high school because math is a use-it-or-lose-it subject. If we stop teaching math in high school and just teach it up to middle school, not only will many people lose their ability to do basic math, but we will have fewer and fewer people get that spark of wonder about math that the author had when taking math for a second time; after having that spark myself, I realized that people start getting the spark once they are in harder math classes. At first, I thought that if math stopped being required in high school, and was offered as an elective, then only people with the spark would continue with it, and everything would be okay. After thinking about the consequences of the idea, I realized that technology requires knowing the seemingly unneeded math. There is already a shortage of IT professionals, and stopping math earlier will only worsen that shortage. Math is tricky. If you try your best to understand it, it isn’t too hard. However, the problem is people had bad math teachers when they were younger, which made them hate math. I have learned that the key to learning math is to have an open mind.

— Andrew, Cary High School

“I think math is a waste of my time because I don’t think I will ever get it.”

In the article Mr. Wilkinson writes, “When I thought about mathematics at all as a boy it was to speculate about why I was being made to learn it, since it seemed plainly obvious that there was no need for it in adult life.” His experience as a boy resonates with my experience now. I feel like math is extremely difficult at some points and it is not my strongest subject. Whenever I am having a hard time with something I get a little upset with myself because I feel like I need to get everything perfect. So therefore, I think it is a waste of my time because I don’t think I will ever get it. At the age of 65 Mr. Wilkinson decided to see if he could learn more/relearn algebra, geometry and calculus and I can’t imagine myself doing this but I can see myself understanding even more how important it is and appreciating it more as I get older. When my dad was young he hated history but, as he got older he learned to appreciate it and see how we can learn from our past mistakes and he now loves learning new things about history.

— Kate, Cary High School

“Not all children need to learn higher level math.”

The higher levels of math like calculus, algebra, and geometry have shaped the world we live in today. Just designing a house relates to math. To be in many professions you have to know algebra, geometry, and calculus such as being an economist, engineer, and architect. Although higher-level math isn’t useful to some people. If you want to do something that pertains to math, you should be able to do so and learn those high levels of math. Many things children learn in math they will never use again, so learning those skills isn’t very helpful … Children went through so much stress and anxiety to learn these skills that they will never see again in their lives. In school, children are using their time learning calculus when they could be learning something more meaningful that can prepare them for life.

— Julyssa, Hanover Horton High School

“Once you understand the basics, more math classes should be a choice.”

I believe that once you get to the point where you have a great understanding of the basics of math, you should be able to take more useful classes that will prepare you for the future better, rather than memorizing equations after equations about weird shapes that will be irrelevant to anything in my future. Yes, all math levels can be useful to others’ futures depending on what career path they choose, but for the ones like me who know they are not planning on encountering extremely high level math equations on the daily, we should not have to take math after a certain point.

— Tessa, Glenbard West High School

“Math could shape the world if it were taught differently.”

If we learned how to balance checkbooks and learn about actual life situations, math could be more helpful. Instead of learning about rare situations that probably won’t come up in our lives, we should be learning how to live on a budget and succeed money-wise. Since it is a required class, learning this would save more people from going into debt and overspending. In schools today, we have to take a specific class that doesn’t sound appealing to the average teenager to learn how to save and spend money responsibly. If it was required in math to learn about that instead of how far Sally has to walk then we would be a more successful nation as a whole. Math could shape the world differently but the way it is taught in schools does not have much impact on everyday life.

— Becca, Bentonville West High School

“To be honest, I don’t see the point in learning all of the complicated math.”

In a realistic point of view, I need to know how to cut a cake or a piece of pie or know how to divide 25,000 dollars into 10 paychecks. On the other hand, I don’t need to know the arc and angle. I need to throw a piece of paper into a trash can. I say this because, in all reality and I know a lot of people say this but it’s true, when are we actually going to need this in our real world lives? Learning complicated math is a waste of precious learning time unless you desire to have a career that requires these studies like becoming an engineer, or a math professor. I think that the fact that schools are still requiring us to learn these types of mathematics is just ignorance from the past generations. I believe that if we have the technology to complete these problems in a few seconds then we should use this technology, but the past generations are salty because they didn’t have these resources so they want to do the same thing they did when they were learning math. So to be honest, I don’t see the point in learning all of the complicated math but I do think it’s necessary to know the basic math.

— Shai, Julia R Masterman, Philadelphia, PA

Learn more about Current Events Conversation here and find all of our posts in this column .

Home — Essay Samples — Science — Mathematics in Everyday Life — Mathematics In Everyday Life: Most Vital Discipline

Mathematics in Everyday Life: Most Vital Discipline

Categories: Mathematics in Everyday Life

About this sample

Words: 795 |

Published: Mar 14, 2019

Words: 795 | Pages: 2 | 4 min read

Works Cited

Benacerraf, P. (1991). Mathematics as an object of knowledge. In P. Benacerraf & H. Putnam (Eds.), Philosophy of mathematics: Selected readings (pp. 1-13). Cambridge University Press.
EdReady. (n.d.). Home. Retrieved from https://www.edready.org/
Puttaswamy, T. K. (2012). Engineering mathematics. Dorling Kindersley (India) Pvt. Ltd.
Steen, L. A. (Ed.). (2001). Mathematics today: Twelve informal essays. Springer Science & Business Media.
Suter, B. W. (2012). Mathematics education: A critical introduction. Bloomsbury Academic.
Tucker, A. W. (2006). Applied combinatorics. John Wiley & Sons.
Vakil, R. (2017). A mathematical mosaic: Patterns & problem solving. Princeton University Press.
Wolfram MathWorld. (n.d.). MathWorld--The web's most extensive mathematics resource. Retrieved from http://mathworld.wolfram.com/
Wu, H. H. (2011). The mis-education of mathematics teachers. Educational Studies in Mathematics, 77(1), 1-20.
Ziegler, G. M., & Aigner, M. (2012). Proofs from THE BOOK. Springer Science & Business Media.

Cite this Essay

Let us write you an essay from scratch

450+ experts on 30 subjects ready to help
Custom essay delivered in as few as 3 hours

Get high-quality help

Prof Ernest (PhD)

Verified writer

Expert in: Science

+ 120 experts online

By clicking “Check Writers’ Offers”, you agree to our terms of service and privacy policy . We’ll occasionally send you promo and account related email

No need to pay just yet!

Related Essays

1 pages / 589 words

1 pages / 649 words

1 pages / 424 words

2 pages / 1068 words

Remember! This is just a sample.

You can get your custom paper by one of our expert writers.

121 writers online

Mathematics in Everyday Life: Most Vital Discipline Essay

Still can’t find what you need?

Browse our vast selection of original essay samples, each expertly formatted and styled

Related Essays on Mathematics in Everyday Life

Background information on field experience school: Miami Coral Park Senior High School has 2,891 students of which 92% are Hispanic, 2% are Black, 4% White, and 2% Asian. 13% of the school’s students are ELL/LEP. The grades [...]

In this 'Mathematics in Architecture' essay, the researcher delves into the question if it is possible for architecture to stand alone without the help of mathematics? This research paper will also determine how Mathematics is [...]

Algebra, a branch of mathematics that involves symbols, equations, and variables, is often met with mixed feelings among students. Some see it as a challenging and abstract subject, while others recognize its practicality and [...]

Mathematics has thousands of branches, and each branch means something different to every person. Some may know it as a useful tool that is a key to getting civilizations rolling. Others may just see it as bothersome and a tough [...]

For this project, Grade 10 Math Project, we have to pick something from real life that I can explain how math affects it. I chose to do my project about the Pharmaceutical industry. The pharmaceutical mathematics curriculum [...]

The spiral model combines the idea of iterative development with the systematic, controlled aspects of the waterfall model. The spiral model has four phases. A software project repeatedly passes through these phases in [...]

Get Your Personalized Essay in 3 Hours or Less!

We use cookies to personalyze your web-site experience. By continuing we’ll assume you board with our cookie policy .

Instructions Followed To The Letter
Deadlines Met At Every Stage
Unique And Plagiarism Free

30,000+ students realised their study abroad dream with us. Take the first step today

Meet top uk universities from the comfort of your home, here’s your new year gift, one app for all your, study abroad needs, start your journey, track your progress, grow with the community and so much more.

Verification Code

An OTP has been sent to your registered mobile no. Please verify

Thanks for your comment !

Our team will review it before it's shown to our readers.

School Education /

Essay on Importance of Mathematics in our Daily Life in 100, 200, and 350 words.

Updated on
Dec 22, 2023

Essay on Importance of Mathematics in our Daily Life

Mathematics is one of the core aspects of education. Without mathematics, several subjects would cease to exist. It’s applied in the science fields of physics, chemistry, and even biology as well. In commerce accountancy, business statistics and analytics all revolve around mathematics. But what we fail to see is that not only in the field of education but our lives also revolve around it. There is a major role that mathematics plays in our lives. Regardless of where we are, or what we are doing, mathematics is forever persistent. Let’s see how maths is there in our lives via our blog essay on importance of mathematics in our daily life.

Table of Contents

1 Essay on Importance of Mathematics in our Daily life in 100 words
2 Essay on Importance of Mathematics in our Daily life in 200 words
3 Essay on Importance of Mathematics in our Daily Life in 350 words

Essay on Importance of Mathematics in our Daily life in 100 words

Mathematics is a powerful aspect even in our day-to-day life. If you are a cook, the measurements of spices have mathematics in them. If you are a doctor, the composition of medicines that make you provide prescription is made by mathematics. Even if you are going out for just some groceries, the scale that is used for weighing them has maths, and the quantity like ‘dozen apples’ has maths in it. No matter the task, one way or another it revolves around mathematics. Everywhere we go, whatever we do, has maths in it. We just don’t realize that. Maybe from now on, we will, as mathematics is an important aspect of our daily life.

Essay on Importance of Mathematics in our Daily life in 200 words

Mathematics, as a subject, is one of the most important subjects in our lives. Irrespective of the field, mathematics is essential in it. Be it physics, chemistry, accounts, etc. mathematics is there. The use of mathematics proceeds in our daily life to a major extent. It will be correct to say that it has become a vital part of us. Imagining our lives without it would be like a boat without a sail. It will be a shock to know that we constantly use mathematics even without realising the same.

From making instalments to dialling basic phone numbers it all revolves around mathematics.

Let’s take an example from our daily life. In the scenario of going out shopping, we take an estimate of hours. Even while buying just simple groceries, we take into account the weight of vegetables for scaling, weighing them on the scale and then counting the cash to give to the cashier. We don’t even realise it and we are already counting numbers and doing calculations.

Without mathematics and numbers, none of this would be possible.

Hence we can say that mathematics helps us make better choices, more calculated ones throughout our day and hence make our lives simpler.

Essay on Importance of Mathematics in our Daily Life in 350 words

Mathematics is what we call a backbone, a backbone of science. Without it, human life would be extremely difficult to imagine. We cannot live even a single day without making use of mathematics in our daily lives. Without mathematics, human progress would come to a halt.

Maths helps us with our finances. It helps us calculate our daily, monthly as well as yearly expenses. It teaches us how to divide and prioritise our expenses. Its knowledge is essential for investing money too. We can only invest money in property, bank schemes, the stock market, mutual funds, etc. only when we calculate the figures. Let’s take an example from the basic routine of a day. Let’s assume we have to make tea for ourselves. Without mathematics, we wouldn’t be able to calculate how many teaspoons of sugar we need, how many cups of milk and water we have to put in, etc. and if these mentioned calculations aren’t made, how would one be able to prepare tea?

In such a way, mathematics is used to decide the portions of food, ingredients, etc. Mathematics teaches us logical reasoning and helps us develop problem-solving skills. It also improves our analytical thinking and reasoning ability. To stay in shape, mathematics helps by calculating the number of calories and keeping the account of the same. It helps us in deciding the portion of our meals. It will be impossible to think of sports without mathematics. For instance, in cricket, run economy, run rate, strike rate, overs bowled, overs left, number of wickets, bowling average, etc. are calculated. It also helps in predicting the result of the match. When we are on the road and driving, mathetics help us keep account of our speeds, the distance we have travelled, the amount of fuel left, when should we refuel our vehicles, etc.

We can go on and on about how mathematics is involved in our daily lives. In conclusion, we can say that the universe revolves around mathematics. It encompasses everything and without it, we cannot imagine our lives.

Deepansh Gautam

Connect With Us

30,000+ students realised their study abroad dream with us. Take the first step today.

Resend OTP in

Need help with?

Study abroad.

UK, Canada, US & More

IELTS, GRE, GMAT & More

Scholarship, Loans & Forex

Country Preference

New Zealand

Which English test are you planning to take?

Which academic test are you planning to take.

Not Sure yet

When are you planning to take the exam?

Already booked my exam slot

Within 2 Months

Want to learn about the test

Which Degree do you wish to pursue?

When do you want to start studying abroad.

January 2024

September 2024

What is your budget to study abroad?

How would you describe this article ?

Please rate this article

We would like to hear more.

Have something on your mind?

Make your study abroad dream a reality in January 2022 with

India's Biggest Virtual University Fair

Essex Direct Admission Day

Why attend .

Don't Miss Out

Mathematization of nature: how it is done

60TH ANNIVERSARY RETROSPECTIVE
Open access
Published: 27 November 2021
Volume 115 , pages 655–664, ( 2021 )

Cite this article

You have full access to this open access article

J. Leo van Hemmen 1

4395 Accesses

2 Citations

3 Altmetric

Explore all metrics

This article has been updated

Natural phenomena can be quantitatively described by means of mathematics, which is actually the only way of doing so. Physics is a convincing example of the mathematization of nature. This paper gives an answer to the question of how mathematization of nature is done and illustrates the answer. Here nature is to be taken in a wide sense, being a substantial object of study in, among others, large domains of biology, such as epidemiology and neurobiology, chemistry, and physics, the most outspoken example. It is argued that mathematization of natural phenomena needs appropriate core concepts that are intimately connected with the phenomena one wants to describe and explain mathematically. Second, there is a scale on and not beyond which a specific description holds. Different scales allow for different conceptual and mathematical descriptions. This is the scaling hypothesis, which has meanwhile been confirmed on many occasions. Furthermore, a mathematical description can, as in physics, but need not be universally valid, as in biology. Finally, the history of science shows that only an intensive gauging of theory, i.e., mathematical description, by experiment leads to progress. That is, appropriate core concepts and appropriate scales are a necessary condition for mathematizing nature, and so is its verification by experiment.

Avoid common mistakes on your manuscript.

1 Introduction: What is the question?

The key question whose answer we want to analyze in this short essay is how the mathematization of nature works. That it works is clear, as many concrete, even famous examples show, but how is it done? In answering this question, we will restrict ourselves to the natural sciences.

Mathematization of nature means that we can mathematically describe natural phenomena at hand and quantify the processes we analyze. In short, numbers in, numbers out. Only mathematics allows us to do so. Since four centuries, physics has shown that mathematization works in the sense that it is highly successful. Far more important, however, is the fact that without its mathematization the impact of physics would have been minor because making quantitative predictions that can be verified experimentally not only allows an internal check that speeds up progress in understanding (through feedback) but also gives rise to applications that can be precisely tailored to the situation at hand. Dijksterhuis ( 1961 ) brilliantly described the significant contributions of Johannes Kepler, Galileo Galilei, and Simon Stevin to the mechanization of our (physical) world picture that reached its final foundation, its crowning achievement, in the work of Isaac Newton ( 1687 ).

For Dijksterhuis ( 1961 ), mechanization meant the development of physics in general, since until the seventeenth-century mechanics was its dominant part. Hence, his focus was on mechanics. His classic (Dijksterhuis 1961 ) shows that mathematization as mathematical description of physical reality concretized as late as about 1600 with Galileo and Stevin, though the first ideas about mechanics already appeared two millennia earlier.

We will take advantage of some concrete but simple examples to illustrate the essential role that core concepts play in reaching such a mathematical description of natural reality. (In the present context, core concepts were also called key concepts but from now on the expression core concepts will be used. A key opens a door and a core is the central part carrying the full weight.) After having consolidated our common understanding, we will turn to verifying how core concepts in conjunction with suitable scales play their essential role in the success of a few but much acclaimed examples taken from Biological Cybernetics , the world’s oldest journal in computational neuroscience. The journal dates back to 1961/63. For instance, Horace Barlow (Cambridge University) and Norbert Wiener (MIT; Cambridge, MA) belong to its founding fathers (van Hemmen 2009 ). A short outlook will gather the insights we have gained.

Science is a quest, a reconnoitering expedition to find so-called logical explanations of phenomena occurring in the world around us. Such a quest is akin to looking for points of orientation and then tracing the outline of an as-yet-unknown landscape. It should be constantly borne in mind that many erudite and learned arguments fill the pages of books on the history and philosophy of science but that here we will simply skip these and pick a few masterpieces or introductions as sign posts in a fascinating landscape. As for the history of mechanics as it leads through many loopholes to Newton’s laws ( 1687 ), the classic The mechanization of the world picture of Dijksterhuis ( 1961 ) will provide the reader with practically all the details needed, and many more. From a more general perspective, the monograph of Simonyi ( 2012 ) paves the way to a grandiose overview of more recent times. For the present purposes, Okasha’s booklet (Okasha 2002 ) suffices as a nice, succinct, philosophical-background reference, also mentioning useful supplementary literature.

2 The solution: core concepts and scaling hypothesis

It is time to delve into the rich soil of concrete examples that illustrate the relevance of core concepts in the context of the scaling hypothesis (van Hemmen 2014 ). We discuss a few core concepts as they play their key role. First, we turn to Newton’s second law because nearly everyone knows this example and can now recognize it as a paradigm. Next, we quickly analyze three examples taken from theoretical neuroscience, viz. a neuron as threshold element, STDP as a canonical learning paradigm, and the population vector code as determinant of motion. All four examples are only valid on a certain scale, which naturally leads us to the scaling hypothesis.

2.1 Core concepts

We embark on analyzing four core concepts. We will then discover that there is a natural scale beyond which our natural laws do not hold.

Momentum & Newton’s laws Many people may remember the cannonball problem from their days in high-school or grammar school: A cannon is placed on a tower of height h and, at time $t=0$ , a cannon shoots a cannon ball of mass m and velocity vector $\mathbf {v} = (v_1, v_2, v_3)$ , pointing upward in some direction. Now solve the problem of determining the ball’s orbit after leaving the cannon and neglecting friction. As we live in a three-dimensional world, the velocity $\mathbf {v}$ and a direction have three components; though accidental, for the present problem two will do as the ball moves in a two-dimensional, vertical, plane spanned by the tower and the direction vector. The reader may remember that, neglecting friction, a parabola was the orbit one was looking for and that this result followed from Newton’s second law. How did that work?

Newton ( 1687 ) formulated his three laws in a monumental work with far-reaching consequences, also for planetary motion. For background information, see the classical work of Dijksterhuis ( 1961 ). Newton’s second law—commonly known as “force equals mass times acceleration”—describes how a particle with mass m and velocity $\mathbf {v}$ moves in three dimensions under the influence of a force $\mathbf {F}$ . Three ingredients are to be noted. First, the force $\mathbf {F}$ is, like $\mathbf {v} = (v_1, v_2, v_3)$ , a vector $\mathbf {F} = (F_1, F_2, F_3)$ with three components since the space in which we live has three dimensions.

Now we need a totally new concept, a core concept, viz. the momentum $\mathbf {p} = m \mathbf {v}$ , which took physics two millennia to discover (Dijksterhuis 1961 ). It was Simon Stevin (1548–1620) who discovered—almost a century before Newton—the importance of momentum (Dijksterhuis 1970 ) in his collision experiments on a frictionless table: The total momentum is conserved. That means that for two (round) disks with momentum $\mathbf {p}$ the sum $\mathbf {p}_1 + \mathbf {p}_2$ is the same before and after the collision; i.e., it is conserved.

Imagine you were an unprejudiced observer around 1600. Along comes Stevin who joyfully tells you that total momentum is conserved in collision experiments. You would turn up your nose and ask yourself: What does this nonsense mean? Mass m has dimension kg and I now need to multiply m by a weird vector $\mathbf {v}$ of dimension m/s in order to get the momentum $\mathbf {p} = m \mathbf {v}$ . Then, along comes Newton ( 1687 ) who brings in a force $\mathbf {F}$ and gives the whole thing a meaning by posing $\mathbf {F} = \mathrm {d}\mathbf {p}/\mathrm {d}t$ , Newton’s second law, where (à la Leibniz) d/d t means differentiation with respect to the time t , a new mathematical idea he brought up independently of Leibniz.

$\mathbf {F} = \mathrm {d}\mathbf {p}/\mathrm {d}t$ is what most people know but need not be aware of yet because for a particle with mass m , position vector $\mathbf {x} = \mathbf {x}(t)$ , where $\mathbf {x}$ generally depends on the time t , and velocity vector $\mathbf {v} = \mathrm {d}\mathbf {x}/\mathrm {d}t$ , we get $\mathbf {F} = \mathrm {d}\mathbf {p}/\mathrm {d}t = m \mathbf {v}/\mathrm {d}t \equiv m \mathbf {a}$ , mass times acceleration $\mathbf {a} = \mathrm {d}^2\mathbf {x}/\mathrm {d}t^2$ with $\mathbf {p} = m \mathbf {v}$ and the mass m constant. Newton’s second law is a universally applicable law of nature. That is, there is no exception...as long as $v/c \ll 1$ where $v = \Vert \mathbf {v}\Vert $ is the particle’s velocity (in m/s) and c is the velocity of light. Already here is the scale disguised as relativity theory lurking in the background.

It is worth noting that, simply put, $\mathbf {F} = \mathrm {d}\mathbf {p}/\mathrm {d}t$ describes the change in momentum $\mathbf {p}$ under the influence of a force $\mathbf {F}$ over time. Mathematics allows us to solve the differential equation $\mathbf {F} = \mathrm {d}\mathbf {p}/\mathrm {d}t$ ; rarely explicitly, but always numerically. The equation $\mathbf {F} = \mathrm {d}\mathbf {p}/\mathrm {d}t$ immediately gives the solution to the cannonball problem as $\mathbf {F} = (0, 0, -g)$ where $g = 9.81$ m/s $^2$ is the gravity constant and $\mathbf {x}(0) = (0,0, h)$ because the cannon was standing on a tower of height h . Newton’s second law also explains the conservation of momentum as Newton postulated his third law as well: $\textit{actio} = -\textit{reactio}$ during collisions. The sum $\mathbf {F}_\mathrm {total}$ of all forces on and, for the collision, in the plane of the (frictionless) table therefore $= 0$ so that $\mathrm {d}(\mathbf {p}_1+\mathbf {p}_2)/\mathrm {d}t = \mathbf {F}_\mathrm {total} = 0$ and $\mathbf {p}_1+\mathbf {p}_2$ is conserved. That is, the conservation of momentum follows.

Neuron as threshold element It is time to turn to biology. More in particular, to computational neuroscience. Let us first focus on one of the, also historically, first core concepts, the neuron as threshold element. At the axon hillock, the axon “leaves” the neuron so as to deliver a neuron’s output to elsewhere. Dropping nearly all historical and other details (Ermentrout and Terman 2010 ; Koch 1999 ), we simply state as an experimental fact that once the membrane potential V ( t ) exceeds a certain threshold $\theta $ , i.e., as soon as $V(t) > \theta $ , the neuron produces a spike, a huge—as compared to the usual mV fluctuations—positive potential jump of about 0.1 V amplitude as compared to the resting potential and lasting for about 1 ms.

Action potentials, or spikes for short, are generated through the coordinated activity of many ion channels (Ermentrout and Terman 2010 ; Koch 1999 ). There is little doubt that single ion channels can be described in surprising detail in the context of biological physics. However, a concerted action of hundreds of ion channels generating a spike is still beyond the horizon of theoretical neurobiology and theoretical biophysics. Accordingly, our scale (sic) is here the neuronal and not the ion-channel one, and we focus on the neuron as a threshold element, meaning that it produces an action potential once its membrane potential V exceeds a certain threshold $\theta $ , the core concept.

A neuron was treated as abstract notion of threshold element as early as McCulloch and Pitts ( 1943 ). McCulloch–Pitts neurons operate in discretized time with 1 ms time bins and outputting either a 1 for an active state, meaning spike emission, or 0 for an inactive state. (The McCulloch–Pitts paper has been quoted by many but read by hardly anybody as the arguments are embedded in the heavily formal language of logic.)

The threshold behavior in conjunction with the spike, which they called the “overshoot,” has also motivated Hodgkin and Huxley to perform their now famous experiments (Hodgkin and Huxley 1952 ; Huxley 2002 ; Meunier and Segev 2002 ). Their work, which was both experimental and theoretical, earned them the Nobel Prize and initiated an overwhelming plethora (Ermentrout and Terman 2010 ; Koch 1999 ) of highly detailed neuron models describing many different situations, all outputting different spike shapes, but—and that is the cardinal issue—exhibiting threshold behavior for the potential V . Their system of four coupled nonlinear differential equations that contains the threshold only implicitly is the result of their brilliant fitting work, dating back to the early fifties, when computers were still in statu nascendi . This is an intellectual achievement that theoreticians can hardly overestimate.

Spike-timing-dependent plasticity (STDP) and its learning window The barn owl (Konishi 1993 ) is a nocturnal predator that azimuthally localizes its prey in the woods with a precision of $1^{\circ }{-}2^{\circ }$ . Azimuthal sound localization uses the time difference between left and right eardrum as direction coding, which therefore depends on the interaural distance L between the two; at present, $L \approx 6$ cm. This time difference is washed out strongly by a wide distribution of delay times before the spikes stemming from left and right eardrum finally meet the neurons at the laminar nucleus, where the first map is to be built through synaptic learning, unless genetic coding would reach such a spatial $\upmu $ s precision, which is beyond scientific imagination, to phrase it friendly.

The usual precision one expects from a bird of which the neuronal system operates with spikes is in the millisecond range but a simple calculation shows that in azimuthal sound localization a barn owl reaches a precision in the $\upmu $ s range, three orders of magnitude better than the ms $=$ millisecond one expects. This is the Konishi paradox. To solve it, spike-timing-dependent plasticity (STDP) was invented (Gerstner et al. 1996 ). Its experimental verification (Markram et al. 1997 ) appeared more than a year later and illustrates that theory may well precede its experimental confirmation. It is far more important, however, that a theory, mathematical (or not), does allow experimental verification, which need not always be the case (Smolin 2006 ).

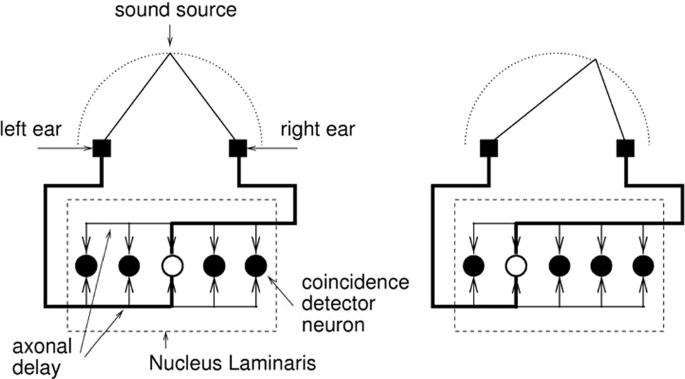
Jeffress model. Schematic anatomy of the barn owl’s laminar nucleus, the first station where axons from left and right ear come together. The figure shows the Jeffress ( 1948 ) idea of converting a time code into a place code: Depending on the direction, different neurons as threshold-coincidence detectors simultaneously get input from left and right so that different directions “ignite” different neurons. The latter are positioned in a one-dimensional row, as are the directions. In reality (Carr and Konishi 1990 ) there are many more (i.e., about 20) neurons than the 5 shown here and many more axons, all parallel to each other, coming from left and right and accidentally connecting each other though synapses that are “in between,” as indicated above

The STDP basics is simple to explain (Kempter et al. 1999 ; van Hemmen 2001 ) and goes as follows. Experimentally, it is known that the young barn owl, once it is able to leave the nest three weeks after hatching, cannot perform the azimuthal sound localization to a precision of $1^{\circ }{-}2^{\circ }$ it would need to survive. After two more weeks, however, it can. What happens during these two weeks?

Synapses need time to develop, to “learn,” which in the barn owl happens during these two critical weeks. In the barn owl’s laminar nucleus, axons stemming ultimately from left or right cochlea and carrying the interaural time-difference (ITD) code through a certain time delay meet for the first time. Let the interaural or, more precisely, the inter-tympanic distance be L and the direction of the sound source with respect to straight on be $\theta $ so that straight on means $\theta = 0$ , then the ITD equals $(L/v_s) \sin \theta $ where $v_s$ is the velocity of sound, about 330 m/s. The time code of the prey (or predator in case of the barn owl’s meal) direction is then contained in $L \sin \theta $ . No more, no less. And the brain has to decode this and tell the animal what to do. In other words, the brain apparently converts the time code contained in $\theta $ into a place code by letting neurons fire when they get their maximal input, i.e., simultaneously from left and right ear. (As the cochlea is in between, this always means modulo the period T of the oscillation.) This is what the anatomy is going to do. The original, so to speak theoretical, idea of converting time code to place code is due to Jeffress ( 1948 ), who published it long before its anatomical confirmation appeared (Carr and Konishi 1990 ).

Returning to the anatomy that is depicted schematically in Fig. 1 , the (vertical, fast) axons turn left or right, so to speak, so as to run parallel to each other with the spike speed now being slowed down and contacting about 20 neurons in a row through excitatory synapses. One needs to keep in mind that here there is no inhibition. The whole anatomical construction is genetically predisposed, though only on a global level, but the barn owl’s $\mu $ s precision is not. By construction, the growth of this anatomical construction depends among others on available food, which fluctuates from day to day, and growth of thousands and thousands of axons connected to the cochlear frequency decomposition, so that genetic coding is out. Now STDP with its learning window W as core concept comes in.

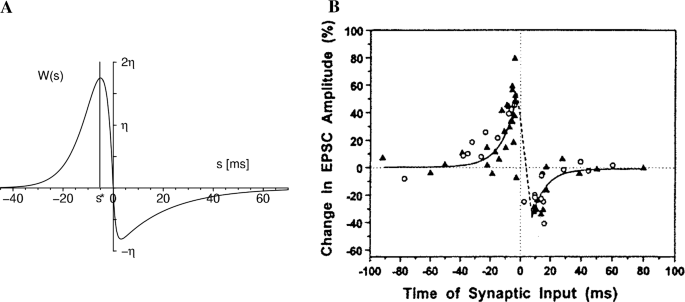
A. STDP’s learning window W in units of the learning parameter $\eta $ as function of the delay $s=t^f_i-t^n$ between presynaptic spike arrival at synapse i at time $t^f_i$ and postsynaptic firing at time $t^n$ . If W ( s ) is positive (negative), for some s the synaptic efficacy $J_i$ is increased (decreased). The increase of the excitatory $J_i$ is most efficient, if a presynaptic spike arrives a few milliseconds before the postsynaptic neuron starts firing (vertical line at $s=s^*$ ). For $|s|\rightarrow \infty $ we have $W(s)\rightarrow 0$ . Taken from Kempter et al. ( 1999 ). B. Experimentally obtained learning window of a cell in rat hippocampus; reprinted by permission (Zhang et al. 1998 ). The similarity to the left figure is evident. It is important to realize that the width of the learning window is to be in agreement with other neuronal time constants. In the auditory system, for instance, these are nearly two orders of magnitude smaller than, e.g., in hippocampus so that the learning window’s width scales accordingly

We focus on synapse i with efficacy $J_i$ and positioned on a certain neuron in the row shown in Fig. 1 and specify how it will change depending on the arrival time $t_i^f$ of a spike at the synapse and the firing time $t^n$ of the postsynaptic neuron it is on. This specification, namely, is the learning window W , a function that can assume either positive or negative values. It is the key to understanding the benign influence of W on the formation of the barn owl’s extremely precise azimuthal map. The speed of this kind of learning can be tuned mathematically by a prefactor $\eta $ so that the actual change is described by $\Delta J_i = \eta W$ . The learning window $W = W(s)$ with $s = t_{i}^{f}-t^{n}$ has a shape as specified by Fig. 2 . For now its precise shape is not important. Only its qualitative appearance counts. That is, $W(s) \ge 0$ is positive for $s = (t_{i}^{f}-t^{n})< 0 \Leftrightarrow t_{i}^{f} < t^{n}$ so that the presynaptic spike arrives before the postsynaptic neuron fires. On the other hand, $W(s) \le 0$ is negative for $s = (t_{i}^{f}-t^{n}) > 0 \Leftrightarrow t^{n} < t_{i}^{f}$ so that the presynaptic spike arrives after the postsynaptic neuron has fired. Colloquially, those who come too late shall be punished.

During map formation, many synapses on a neuron in the laminar nucleus are steered by coherent input of a specific frequency stemming from the frequency decomposition performed by the cochlea of left and right ear(drum)s. For a specific rotation angle $\theta $ of the head, the time delay between left and right eardrum is fixed but at the start of the critical period of two weeks for synaptic learning in the barn owl’s brain there is a huge scatter in time delays along different axons. In general, this wetware cannot change but the synapses can. Figure 3 shows what happens as time proceeds: The “good” ones among the synapses are strengthened and the “bad” one are weakened, which is due to the positive and negative part, respectively, of the learning window W .

Because in the barn owl phase locking of the cochlear neurons happens up to 9 kHz, the temporal resolution is far better than in, say, human ears. (Though phase locking in humans and most other vertebrates is restricted to $\le 1.5$ kHz, humans have more brains, through which they compensate their wetware deficit and become as good as barn owls, with a spatial resolution of $1^{\circ }{-}2^{\circ }$ for azimuthal sound localization.) Though in the case of the barn owl’s laminar nucleus all synapses are excitatory, in the auditory system of mammals inhibition plays a role as well and STDP can be adapted accordingly; see, e.g., Leibold and van Hemmen ( 2005 ).

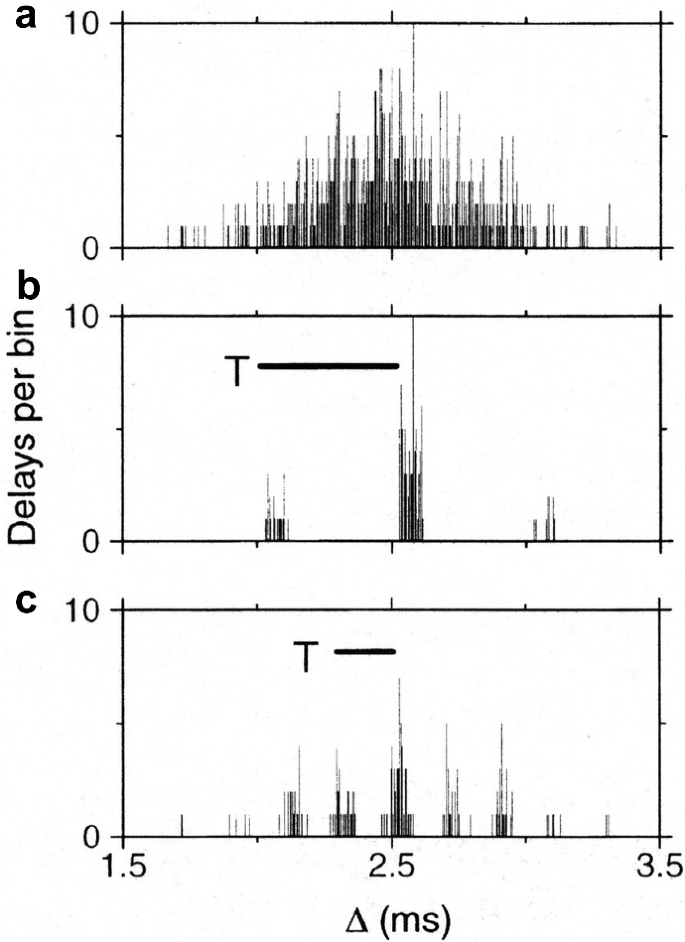
Evolution of synaptic strengths and “survival of the fittest” in the young barn owl’s laminar nucleus during its critical period. a Before learning, there are 600 synapses with a Gaussian distribution ( $2.5 \pm 0.3$ ms) of the synaptic strengths connected to a single neuron, binned as a function of the signal-transmission delays w.r.t. arrival at left and right eardrum. b After a learning session from a stimulus of 2 kHz, only 105 synapses survive. They have delays that differ by multiples of the period $T = 500\,\upmu \hbox {s}$ (scale bar); phrased differently, modulo the period T everything in an oscillation is identical. The output spikes exhibit phase locking with a vector strength (van Hemmen 2013 ) of 0.97 corresponding to a temporal precision of $20\,\upmu \hbox {s}$ . c Analogous to b but now for an input frequency of 5 kHz. Figure and data taken from Gerstner et al. ( 1996 ), Fig. 2, who also show how in subsequent nuclei the temporal precision can be increased by an order of magnitude

Not only does STDP describe the learning dynamics of individual synapses in that it tunes them so as to fit their spatiotemporal surroundings but, as Fig. 3 shows for a single neuron, it also governs how many synapses and which ones operate in concert so as to build a topographic map. To obtain a full map, however, synapses on different neurons also need—so to speak—to tell each other what they are doing, through a kind of retrograde signaling (Fitzsimonds and Poo 1998 ). In the barn-owl case (Kempter et al. 2001 ), this means that along the string of parallel axons coming from left and right ear the synapses connected to the very same presynaptic axon communicate their positive or negative change to their neighbors and in this way influence each other, a mechanism called axon-mediated synaptic leaning (AMSL). That is, given a suitable anatomy an ITD map with the required topographic precision emerges from a combined action of homosynaptic spike-based Hebbian learning through STDP together with AMSL as its propagator along the presynaptic axons.

As a final note, STDP also gives rise to (Wenisch et al. 2005 ) a full explanation of how direction-selective spatiotemporal maps come about in primary visual cortex V1. The interplay of the anatomy of excitation and slightly longer-ranged inhibition and STDP is essential to giving rise to a spatiotemporal map. This fact shows again the potency of STDP as core concept in synaptic learning and map formation (van Hemmen 2006 ). As shown by Wenisch et al. ( 2005 ), map formation in V1 is mainly a matter of self-organization based on specific neuroanatomy in conjunction with STDP that then gives rise to the spatiotemporal receptive fields from which the whole map arises, as confirmed by experiment.

Population vector code The population vector code relates directional tuning of single cells to global, directional motion induced by an assembly (Hebb 1949 ) of neurons. The scale we now focus on is that of an assembly of neurons; in this case, in motor cortex (Georgopoulos et al. 1986 ; van Hemmen and Schwartz 2008 ). The underlying geometric idea is appealingly simple and its predictions are extremely powerful. Let us assign to each motor neuron with label i its preferred direction $\mathbf {e}_i$ , a unit vector. It is a priori not evident that one can assign such a vector but experimental evidence has shown one can (Georgopoulos et al. 1986 ; van Hemmen and Schwartz 2008 ). For an assembly (Hebb 1949 ) or population of motor neurons $\{1 \le i \le N\}$ with momentary firing rate $\nu _i = \nu _i(t)$ , the weighted vector sum, the so-called population vector $\mathbf {n}$

encodes the direction $ \mathbf {e}$ of movement resulting from an assembly of motor neurons, while $\nu $ , the length of the population vector $\mathbf {n}$ , is proportional to the instantaneous speed of the drawing motion we focus on.

That is, $\mathbf {n}$ predicts the grasping direction or the direction an animal would like to choose (van Hemmen and Schwartz 2008 ) for catching its prey, be it the barn owl ( Tyto alba ), the back swimmer ( Notonecta undulata ) or the sand scorpion ( Paruroctonus mesaensis ). In fact, for all these animals it has been shown that the population vector applied to the sensory instead of the motor system of the animal already predicts its prey-catching behavior (Stürzl et al. 2000 ; van Hemmen and Schwartz 2008 ; van Hemmen 2014 ). In other words, the population vector code functions as a neuronal actuator. An extra advantage is that sensory and motor system would use the same coding, which makes this correspondence principle even more plausible.

2.2 Scaling hypothesis

The scaling hypothesis (van Hemmen 2014 ) formulates what is known from many examples, but since a definitive proof cannot be provided we are forced to formulate it as hypothesis: There is a scale on and not beyond which a specific description holds. Different scales need different conceptual and mathematical descriptions. We have just seen a few examples as illustration in that the previous core concepts only function on a certain scale. The population vector code functions on the population level is three orders of magnitude larger than the neuronal one of threshold principle and STDP.

The most outspoken examples of the correctness of the scaling hypothesis are still provided by physics. It is meanwhile known that Newton’s second law $\mathbf {F} = \mathrm {d}\mathbf {p}/\mathrm {d}t$ only holds for (i) velocities $|\mathbf {v}|/c \ll 1$ and (ii) spatial scales down to $0.1\,\upmu \hbox {m}$ . Six orders of magnitude smaller than our macroscopic world (of 1 m), i.e., in the nm range, dynamics is governed by quantum mechanics, which has some relations to our macroscopic world but also needs new and totally different principles such as its probability interpretation that have no resemblance to what we are macroscopically used to. That is, these principles cannot be derived but must be taken as “naturally” given, as is Newton’s law. Adding relativity one obtains an even richer structure. Again six orders of magnitude smaller, we arrive at quantum chromodynamics (QCD) and the so-called standard model, viz., of elementary articles and quarks, their mathematical description stemming from quantum field theory. What is beyond, be it space or time (think of origin of the universe) is a heavily debated domain of research.

2.3 Core concepts are—usually—only valid on a certain scale and stand by themselves

It is time for a tentative summary. We have seen that core concepts are a necessary condition for the mathematization of nature. They need to be “rightly” chosen, which may take time; even lots of time (Dijksterhuis 1961 ). Furthermore, their validity is bound to a certain scale in space and/or time, beyond which they do not hold. It may also take lots of patience (Simonyi 2012 ) to discover such a scale. One really outspoken example may do for now.

More than a century ago physicists discovered in the context of radiation—think of Max Planck’s 1900 introduction of his novel constant $h = 2\pi \, \hbar $ —that Newton’s mechanics apparently does not hold on the scale of atoms and molecules. The question of what could replace classical mechanics tantalized physics for three decades before a novel kind of physics, since then called quantum mechanics, was discovered during the years 1927–1929. The corresponding probabilistic interpretation, most notably, the highly successful one due to the Kopenhagen School of Niels Bohr, has been confirmed experimentally in all details, but nevertheless even the genius of Einstein was not able to accept it (mainly because of his misinterpretation of the notion of chance). As noted, beyond quantum mechanics, on a scale six orders of magnitude smaller, we enter the QCD domain. Each domain has its own rules, which cannot be derived from the “coarser” one, despite having relations with it. That is, the rules exist in their own right.

Neuroscience also has many scales, viz. that of ion channels, that of neurons, that of assemblies of neurons,.... Their scales are separated by orders of magnitude. There are relations, maybe even intimate ones, between the descriptions on different scales. Here we do not aim at ‘scales’ in the technical sense of nonlinear dynamics but at those as they exist for instance between classical mechanics à la Newton and quantum mechanics; see, e.g., van Hemmen ( 2014 ). These different scales have descriptions in their own right . They cannot be derived fully from theories that are valid on a larger or smaller scale, be that in space or time. This is what one may call the ‘principle of scientific independence’ or, for short, the independence principle.

For example, the probabilistic interpretation of quantum mechanics exists in its own right. Einstein may have grumbled “God does not play dice” but the simple reply is: Why not? Deciding that is neither up to Einstein, nor to you, nor to anybody else. Only experiment decides. End of the discussion.

From the present point of view, (many of) the “laws” of psychology exist in their own right and there is little hope that they will ever be straightforwardly “derived” from neuroscience, which focuses its attention on much smaller scales. That is, there are doubtlessly many relations between phenomena on the neuronal and, hence, also on the macromolecular level—c.f. neuromicrobiology—and the behavior of humans, and other animals, but psychology has several independent(ly existing) notions describing behavior that only exist by themselves—on the macroscopic scale of psychology. Freud sends greetings.

3 More core concepts from theoretical neurobiology

It is now time to harvest core concepts while noticing the appropriate scales. We do so by analyzing some highly acclaimed papers that have appeared as ripe, tasty, fruits in Biological Cybernetics , the world’s oldest journal in computational neuroscience, which has meanwhile reached the respectable age of 60 years and 115 volumes. Nearly all of these examples exhibit a core concept and do so in the context of a specific scale. For additional comments, see Koenderink ( 2021 ), Kelso ( 2021 ), Wilson and Cowan ( 2021 ), Baccalá and Sameshima ( 2021 ), Humphries and Gurney ( 2021 ), von der Malsburg ( 2021 ) and Abarbanel ( 2021 ).

Scale space Eyes behold the three-dimensional world through a two-dimensional projection onto the retina, an image. Images may be blurred or distorted, for instance, because of unlucky illumination of a scene, or bad quality of the eye lens, or noise, or a combination of all together. Since the mathematical theory of image processing is of fundamental importance—not only to vision!—Koenderink ( 1984 ) apparently chose Biological Cybernetics (BC) for publishing his essay “The structure of images.”

Here he implemented—cf. Koenderink ( 2021 )—the core concept of scale space that Witkin ( 1983 ) had introduced the year before. In doing so, he noticed how important Gaussian were in this game and realized that Gaussians have a unique property that comes in a minute. Introducing the mathematical framework of the diffusion equation for functions defined on the plane $\mathbb {R}^2$ , he developed a full-blown theory incorporating and explaining, and in this way integrating, many experimental facts that were already known. His bright observation was that a Gaussian is the Green’s function of a two-(or n )-dimensional Laplacian, so to speak the infinitesimal generator of blurring. [A Green’s function or fundamental solution (Evans 2015 , §2.3, Eq. (13)) is an integral kernel $\Phi $ providing an explicit solution to, e.g., $(\partial _t - \Delta ) u = f$ with initial condition $u(t=0)=0$ through $u (\mathbf {x}, t) = \int \mathrm {d}\mathbf {y} \mathrm {d}s \, \Phi (\mathbf {x} - \mathbf {y}, t -s) f(\mathbf {y},s)$ .]

In summary, here the core concept is ‘scale space’ and the scale of image analysis is macroscopic, $\mathbb {R}^2$ or, if you like, the retina plane.

Haken, Kelso, Bunz & the HKB model The best you can do in getting famous or at least well known in science is inventing a model that carries your name. Good papers in BC need a while to take off, meaning that their content is novel, but they then fly quite long, which in fact is a proven characteristic of many BC papers.

Haken et al. ( 1985 ) invented a model that now carries their names, viz., HKB. They did not derive but simply posed it so as to mathematically describe hand movements. It is a mathematically simple looking model of two coupled nonlinear ordinary differential equations of the oscillator type, with a bit of noise to incorporate many unknown, external, influences, and describing hand movements; it can be reduced to a single equation for the relative phase between two fingers. The HKB equations contain some cleverly chosen parameters that allow reproducing some experiments that Kelso and coworkers had performed and published a few years earlier. Many more experiments followed, a few of which are described and commented by Kelso ( 2021 ).

Clearly, the scale is macroscopic and so is that of the equations. The question of how to derive equations of the HKB type neuronally is still a challenge but, as argued in Sect. 2.3 , this may, but need not, happen. What then remains is a valuable quantitative description on a certain scale, the macroscopic scale of hand movements.

Wilson–Cowan equations and the continuum limit Neurons are discrete entities in a three-dimensional continuum. On the other hand, continuum descriptions allow application of powerful mathematical techniques related to the mathematics of pattern formation (Hoyle 2006 ). The Wilson and Cowan ( 1973 ) equations offer a continuum description of neuronal reality consisting of continuum variables that describe two populations of excitatory and inhibitory neurons. As such they are meanwhile well-known and widely used. As Wilson and Cowan ( 2021 ) confessed, they aimed from the very beginning to, among others, traveling waves as possible solutions—in view of nature, rightly so. The scale is, say, neuronal and so are the equations.

Hallucinations, a popular topic in the seventies, provide a nice example and the Wilson–Cowan equations were shown (Wilson and Cowan 2021 ) to allow the typical hallucinatory patterns as solutions. One need to admit, though, that the continuity of space is immaterial as a lattice of discrete neurons allows the very same patterns as solutions (Fohlmeister et al. 1995 ).

Neurons being discrete entities, a far more fundamental question is whether the popular Wilson–Cowan equations could be mathematically derived from a discrete model through a continuum limit. There are examples in applied mathematics, as tour de force far beyond the present context, that allow such a limit. Nevertheless, an early ansatz in this direction of a rigorous proof already exists since long (van Hemmen 2004 ).

Partial directed coherence = PDC Uncovering coherence such as the simultaneous, i.e., within a small time window, spiking of many neurons has been proven invaluable to neuroscience for understanding collective behavior under the influence of homogeneous (e.g., a pure tone) or correlated input. One does so by analyzing many-neuron time series of very many spikes that are considered as point events. Machine learning and, thus, high computer power are meanwhile essential in sorting the huge amounts of spike data.

Because of the inherent uncertainty that experimental data contain, statistics comes in as well. And one needs sorting criteria. Granger ( 1969 ) was one of the first to perform such an analysis. He introduced a statistical hypothesis test within the context of economics; see also his later comments (Granger 1980 ). It was within the Granger context that Baccalá and Sameshima ( 2001 ) introduced their novel core concept of ‘partial directed coherence’ (PDC) ensuing from their multivariate time-series analysis based on a decomposition of multivariate partial coherences. Hence, the name PDC.

This makes sense because, as Granger ( 1980 ) also pointed out himself on a later occasion, instead of talking about causality, i.e., X causes Y, the Granger causality actually tests whether X forecasts Y. Causality—what is that precisely?—implies prediction but probability is always dangling in the background. Neuroscience sends greetings to economics. The core concept as introduced by Baccalá and Sameshima ( 2001 ) and reconsidered by Baccalá and Sameshima ( 2021 ) is now ‘partial directed coherence’ and, for time series of spikes, the scale is neuronal.

Basal ganglia and the GPR model GPR stands for three authors, Gurney, Prescott, and Redgrave who published an anatomy-based model of action selection in what Humphries and Gurney ( 2021 ) aptly called “the dark basement of the brain,” the basal ganglia [for a clear sketch of the anatomy, see Fig. 1 of Humphries and Gurney ( 2021 )], where an essential part of the motor program is “written.” The GPR paper does what a modern theoretical-neuroscience paper should do: Specifying the essential part of the anatomy so as to make the mathematical model, and doing the job.

Orientation selection in primary visual cortex V1 as a self-organizing process Focusing on primary visual cortex V1 of primates, von der Malsburg ( 1973 ) asked how its orientation map might come about. He devised a concrete model with 338 neurons that are described by a rate and not by a ms-time code and getting input from a “retina” of 19 cells that encode a direction. The interaction structure was patterned after the V1 anatomy in that the range of the excitatory near-neigbor interactions was shorter than that of the inhibitory interactions engulfing them. Finally, learning was going to happen in the original Hebbian sense (Hebb 1949 , p 62),

When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes part in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.

Hebb continued by suggesting “synaptic knobs develop.” The synapse being at an end of an axon stemming from neuron A, it has a presynaptic part and a postsynaptic part at the other side of the synaptic cleft, sitting on neuron B. So it all fit. Therefore von der Malsburg ( 1973 ) took A’s firing rate. We note, though, that timing played no role in Hebb’s proposal, whereas it is essential in STDP (Gerstner et al. 1996 ; Markram et al. 1997 ; Zhang et al. 1998 ). Neither does the de crease of synaptic strength for those spikes that “come too late,” after the postsynaptic neuron has fired.

Given the, from the present point of view, tiny size of computers at that time the project was courageous because only through numerical simulations could even a qualitative orientation map be shown to exist. Given the relatively simple but clearly structured theoretical setup, the result was astounding in that it sufficed to generate self -organized orientation-map formation à la Hubel and Wiesel ( 1962 , 1963 ). The main contribution of von der Malsburg ( 1973 ) can be described succinctly by the title “Towards understanding the neural code of the brain” of his recent paper (von der Malsburg 2021 ).

Mathematically showing self-organization on the basis of known anatomical structures and mechanistic principles was an early (1973) stimulus for many and showed that mathematization works, leading to a far deeper understanding of the phenomena one wants to explain. The point is that, once a structure such as an orientation map has been shown to arise out of the chosen setup, one can quantitatively verify the influence of varying different parameters representing different aspects of the underlying structure. Assigning numerical values to parameters, the fewer the better, in a responsible manner is a technique by itself but not an issue here.

The above examples show both that mathematization of nature works and how it is done. Examples only sample and never depict all of natural reality, nor how scientists analyze it. After all, science is not made by abstract names but by humans. The story of Abarbanel ( 2021 ) highlights how personal interaction between the different actors in a specific domain are essential in moving the carriage of science forward. Furthermore, an intensive interaction between theory and experiment is essential to increasing our insight. Just remember Galileo’s famous, maybe even fabulous, experiment of dropping two masses of different weight from the Tower of Pisa. They arrived simultaneously at the ground and in this way refuted all previous theories.

The present paper has tried to indicate what scientific insight in the sense of mathematization of nature means: uncovering core concepts and the scale on which they act. The rest has to be filled out by the actors of science.

Change history

03 december 2021.

textual change

Abarbanel HDI (2021) A personal retrospective on the 60th anniversary of the journal Biological Cybernetics. Biol Cybern 115:205–206

PubMed Google Scholar

Baccalá LA, Sameshima K (2001) Partial directed coherence: a new concept in neural structure determination. Biol Cybern 84:463–474

Baccalá LA, Sameshima K (2021) Partial directed coherence: twenty years on some history and an appraisal. Biol Cybern 115:195–204

Carr CE, Konishi M (1990) A circuit for detection of interaural time differences in the brain stem of the barn owl. J Neurosci 10(10):3227–3246

CAS PubMed PubMed Central Google Scholar

Dijksterhuis EJ (1961) The mechanization of the world picture. Oxford University Press, Oxford. The German translation Die Mechanisierung des Weltbildes was published by Springer (Heidelberg) in 1956. For the Dutch original, De mechanisering van het wereldbeeld (Meulenhoff, Amsterdam, 1950) the author received the Dutch state prize for literature (P.C. Hooft Prize) in 1952

Dijksterhuis EJ (1970) Simon Stevin: science in the Netherlands around 1600. Martinus Nijhoff, Den Haag

Google Scholar

Ermentrout GB, Terman DH (2010) Mathematical foundations of neuroscience. Springer, New York

Evans LC (2015) Partial differential equations, 2nd edn. American Mathematical Society, Providence

Fitzsimonds RM, Poo M (1998) Retrograde signaling in the development and modification of synapses. Physiol Rev 78:143–170

CAS PubMed Google Scholar

Fohlmeister C, Ritz R, Gerstner W, van Hemmen JL (1995) Spontaneous excitations in the visual cortex: stripes, spirals, rings, and collective bursts. Neural Comput 7:905–914

Georgopoulos AP, Schwartz AB, Kettner RE (1986) Neuronal population coding of movement direction. Science 233:1416–1419

Gerstner W, Kempter R, van Hemmen JL, Wagner H (1996) A neuronal learning rule for sub-millisecond temporal coding. Nature 383:76–78

Granger CWJ (1969) Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37(3):424–438

Granger CWJ (1980) Testing for causality: a personal viewpoint. J Econ Dyn Control 2:329–352

Gurney K, Prescott TJ, Redgrave P (2001) A computational model of action selection in the basal ganglia I: a new functional anatomy & A computational model of action selection in the basal ganglia II: analysis and simulation of behaviour. Biol Cybern 85:401–410 & 411–423

Haken H, Kelso JAS, Bunz H (1985) A theoretical model of phase transitions in human hand movements. Biol Cybern 51:347–356

Hebb DO (1949) The organisation of behavior—a neurophysiological theory. Wiley, New York

Hodgkin AL, Huxley AF (1952) A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117:500–544

Hoyle RB (2006) Pattern formation—an introduction to methods. Cambridge University Press, Cambridge

Hubel DH, Wiesel TN (1962) Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol (Lond) 160:106–154

Hubel DH, Wiesel TN (1963) Receptive fields of cells in striate cortex of very young, visually inexperienced kittens. J Neurophysiol 26:994–1002

Humphries MD, Gurney K (2021) Making decisions in the dark basement of the brain: a look back at the GPR model of action selection and the basal ganglia. Biol Cybern 115:323–329

Huxley A (2002) From overshoot to voltage clamp. Trends Neurosci 25:553–558

Jeffress LA (1948) Mechanisms of sound localization. A place theory of sound localization. J Comp Physiol Psychol 42:35–39

Kelso JAS (2021) The Haken–Kelso–Bunz (HKB) model: from matter to movement to mind. Biol Cybern 115:305–322

Kempter R, Gerstner W, van Hemmen JL (1999) Hebbian learning and spiking neurons. Phys Rev E 59:4498–4514

CAS Google Scholar

Kempter R, Leibold C, Wagner H, van Hemmen JL (2001) Formation of temporal feature maps by axonal propagation of synaptic learning. Proc Natl Acad Sci USA 98:4166–4171

Koch C (1999) Biophysics of computation. Oxford University Press, New York

Koenderink J (1984) The structure of images. Biol Cybern 50:363–370

Koenderink J (2021) The structure of images: 1984–2021. Biol Cybern 115:117–120

Konishi M (1993) Listening with two ears. Sci Am 268(4):34–41

Leibold C, van Hemmen JL (2005) Spiking neurons learning phase delays: how mammals may develop auditory time-difference sensitivity. Phys Rev Lett 94:168102

Markram H, Lübke J, Frotscher M, Sakmann B (1997) Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275:213–215

McCulloch WS, Pitts WH (1943) A logical calculus of ideas immanent in nervous activity. Bull Math Biophys 5:115–133

Meunier C, Segev I (2002) Playing the Devil’s advocate: is the Hodgkin–Huxley model useful? Trends Neurosci 25:558–563

Newton I (1687) Philosophae naturalis principia mathematica. Streater, London

Okasha S (2002) Philosophy of science: a very short introduction. Oxford University Press, Oxford

Simonyi K (2012) A cultural history of physics. CRC Press, Boca Raton

Smolin L (2006) The author is a very outspoken critic of modern string theory, which does not allow experimental verification (yet). The trouble with physics. Houghton Mifflin Harcourt, Boston

Stürzl W, Kempter R, van Hemmen JL (2000) Theory of arachnid prey localization. Phys Rev Lett 84:5668–5671

van Hemmen JL (2001) Theory of synaptic plasticity. In: Moss F, Gielen S (eds) Handbook of biological physics, vol 4: neuro-informatics, neural modelling. Elsevier, Amsterdam, pp 771–823

van Hemmen JL (2004) Continuum limit of discrete neuronal structures: is cortical tissue an “excitable” medium? Biol Cybern 91:347–358

van Hemmen JL (2006) What is a neuronal map, how does it arise, and what is it good for? In: van Hemmen JL, Sejnowski TJ (eds) 23 problems in systems neuroscience. Oxford University Press, New York, pp 83–102

van Hemmen JL (2009) Editorial to volume 100 of Biological Cybernetics. Biol Cybern 100:1–3

van Hemmen JL (2013) Vector strength after Goldberg, Brown, and von Mises: biological and mathematical perspectives. Biol Cybern 107(2013):385-396

van Hemmen JL (2014) Neuroscience from a mathematical perspective: key concepts, scales and scaling hypothesis, universality. Biol Cybern 108:701–712

van Hemmen JL, Schwartz AB (2008) Population vector code: a geometric universal as actuator. Biol Cybern 98:509–518

von der Malsburg C (1973) Self-organization of orientation sensitive cells in the striate cortex. Kybernetik 14:85–100

von der Malsburg C (2021) Toward understanding the neural code of the brain. Biol Cybern 115:439–449

Wenisch OG, Noll J, van Hemmen JL (2005) Spontaneously emerging direction selectivity maps in visual cortex through STDP. Biol Cybern 93:239–247

Wilson HR, Cowan JD (1973) A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13:55–80

Wilson HR, Cowan JD (2021) Evolution of the Wilson–Cowan equations. Biol Cybern. https://doi.org/10.1007/s00422-021-00913-6

Article PubMed Google Scholar

Witkin AP (1983) Scale-space filtering. In: Proc Intern Joint Conf Artificial Intelligence (IJCAI), 1019–1021, Karlsruhe 1983. At present the paper is easily found in and downloaded from the internet

Zhang LI, Tao HW, Holt CE, Harris WA, Poo M (1998) A critical window for cooperation and competition among developing retinotectal synapses. Nature 395:37–44

Download references

Acknowledgements

It is a great pleasure to the author to thank Benjamin Lindner for valuable constructive criticism and his long-time collaborator and friend Bruce A. Young for convincing him of making the title of this essay as short as possible.

Open Access

This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Open Access funding enabled and organized by Projekt DEAL.

Author information

Authors and affiliations.

Physik Department T35, Technische Universität München, 85747, Garching bei München, Germany

J. Leo van Hemmen

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. Leo van Hemmen .

Additional information

Communicated by Benjamin Lindner.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The article by former Editor-in-Chief Leo van Hemmen concludes our series of retrospective pieces, celebrating the journal’s 60’s anniversary. We trust the reader will enjoy this first-person account of the history of big ideas in Biological Cybernetics.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

van Hemmen, J.L. Mathematization of nature: how it is done. Biol Cybern 115 , 655–664 (2021). https://doi.org/10.1007/s00422-021-00914-5

Download citation

Published : 27 November 2021

Issue Date : December 2021

DOI : https://doi.org/10.1007/s00422-021-00914-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Mathematization
Core concepts
Scaling hypothesis

Find a journal
Publish with us
Track your research

Home / Essay Samples / Science / Mathematics in Everyday Life / The Presence of Math in Nature and People’s Life

The Presence of Math in Nature and People's Life

Category: Science
Topic: Mathematical Models , Mathematics in Everyday Life

Pages: 2 (975 words)

Downloads: -->

--> ⚠️ Remember: This essay was written and uploaded by an--> click here.

Found a great essay sample but want a unique one?

are ready to help you with your essay

You won’t be charged yet!

Microbiology Essays

Photosynthesis Essays

Cell Essays

Natural Selection Essays

Biodiversity Essays

Related Essays

We are glad that you like it, but you cannot copy from our website. Just insert your email and this sample will be sent to you.

By clicking “Send”, you agree to our Terms of service and Privacy statement . We will occasionally send you account related emails.

Your essay sample has been sent.

In fact, there is a way to get an original essay! Turn to our writers and order a plagiarism-free paper.

samplius.com uses cookies to offer you the best service possible.By continuing we’ll assume you board with our cookie policy .--> -->

Nature by numbers: The hidden beauty of mathematics

Leave a Reply Cancel reply

The Power of Mathematics: Unveiling its Influence on Nature and Phenomena

Table of contents

Cite this Essay

Related Essays

Search form

You are here

V. I. Arnold

Dummy View - NOT TO BE DELETED

MAA Publications

Connect with MAA

Mathematics and the environment

Professional appointments

Read more about:

Essay on Importance of Mathematics in Our Daily Life

100 Words Essay on Importance of Mathematics in Our Daily Life

Mathematics in Daily Tasks

Mathematics in Professions

Mathematics in Decision Making

250 Words Essay on Importance of Mathematics in Our Daily Life

A Tool for Logical Reasoning

Mathematics in Technological Advancements

Financial Management and Mathematics

Mathematics and Scientific Understanding

500 Words Essay on Importance of Mathematics in Our Daily Life

The Ubiquity of Mathematics

Mathematics in the Professional Sphere

Mathematics and Problem-Solving

Mathematics and Critical Thinking

Mathematics and the Digital Age

Leave a Reply Cancel reply

Essay: The Relationship between Math and Nature

Related Posts

Recent Posts

What Students Are Saying About the Value of Math

“Math is a valuable tool and function of the world.”

“Math isn’t about taking derivatives or solving for x, it’s about having the skills to do so and putting them to use elsewhere in life.”

“Just stop and consider your hobbies and pastimes … all of it needs math.”

“Math gives us a different perspective on everyday activities.”

“Math teaches us how to think.”

“Math is a valuable tool for everyone to learn, but students need better influences to show them why it’s useful.”

“At the roots of math, it teaches people how to follow a process.”

“I see now that math not only works through logic but also creativity.”

“In some word problems, I encounter problems that thoroughly interest me.”

“Without high school classes, fewer people get that spark of wonder about math.”

“I think math is a waste of my time because I don’t think I will ever get it.”

“Not all children need to learn higher level math.”

“Once you understand the basics, more math classes should be a choice.”

“Math could shape the world if it were taught differently.”

“To be honest, I don’t see the point in learning all of the complicated math.”

Mathematics in Everyday Life: Most Vital Discipline

Works Cited

Cite this Essay

Related Essays

Still can’t find what you need?

Related Essays on Mathematics in Everyday Life

Related Topics

Get Your Personalized Essay in 3 Hours or Less!

30,000+ students realised their study abroad dream with us. Take the first step today

Essay on Importance of Mathematics in our Daily Life in 100, 200, and 350 words.

Essay on Importance of Mathematics in our Daily life in 100 words

Essay on Importance of Mathematics in our Daily life in 200 words

Essay on Importance of Mathematics in our Daily Life in 350 words

Deepansh Gautam

Connect With Us

30,000+ students realised their study abroad dream with us. Take the first step today.

Need help with?

Country Preference

Which English test are you planning to take?

When are you planning to take the exam?

Which Degree do you wish to pursue?

What is your budget to study abroad?

Make your study abroad dream a reality in January 2022 with

Essex Direct Admission Day

Mathematization of nature: how it is done

Cite this article

1 Introduction: What is the question?

2 The solution: core concepts and scaling hypothesis

2.1 Core concepts