what is number representation in computer

Data Representation in Computer: Number Systems, Characters, Audio, Image and Video

Table of Contents

• 1 What is Data Representation in Computer?
• 2.1 Binary Number System
• 2.2 Octal Number System
• 2.3 Decimal Number System
• 2.4 Hexadecimal Number System
• 3.4 Unicode
• 4 Data Representation of Audio, Image and Video
• 5.1 What is number system with example?

What is Data Representation in Computer?

A computer uses a fixed number of bits to represent a piece of data which could be a number, a character, image, sound, video, etc. Data representation is the method used internally to represent data in a computer. Let us see how various types of data can be represented in computer memory.

Before discussing data representation of numbers, let us see what a number system is.

Number Systems

Number systems are the technique to represent numbers in the computer system architecture, every value that you are saving or getting into/from computer memory has a defined number system.

A number is a mathematical object used to count, label, and measure. A number system is a systematic way to represent numbers. The number system we use in our day-to-day life is the decimal number system that uses 10 symbols or digits.

The number 289 is pronounced as two hundred and eighty-nine and it consists of the symbols 2, 8, and 9. Similarly, there are other number systems. Each has its own symbols and method for constructing a number.

A number system has a unique base, which depends upon the number of symbols. The number of symbols used in a number system is called the base or radix of a number system.

Let us discuss some of the number systems. Computer architecture supports the following number of systems:

Binary Number System

Octal number system, decimal number system, hexadecimal number system.

A Binary number system has only two digits that are 0 and 1. Every number (value) represents 0 and 1 in this number system. The base of the binary number system is 2 because it has only two digits.

The octal number system has only eight (8) digits from 0 to 7. Every number (value) represents with 0,1,2,3,4,5,6 and 7 in this number system. The base of the octal number system is 8, because it has only 8 digits.

The decimal number system has only ten (10) digits from 0 to 9. Every number (value) represents with 0,1,2,3,4,5,6, 7,8 and 9 in this number system. The base of decimal number system is 10, because it has only 10 digits.

A Hexadecimal number system has sixteen (16) alphanumeric values from 0 to 9 and A to F. Every number (value) represents with 0,1,2,3,4,5,6, 7,8,9,A,B,C,D,E and F in this number system. The base of the hexadecimal number system is 16, because it has 16 alphanumeric values.

Here A is 10, B is 11, C is 12, D is 13, E is 14 and F is 15 .

Data Representation of Characters

There are different methods to represent characters . Some of them are discussed below:

The code called ASCII (pronounced ‘􀀏’.S-key”), which stands for American Standard Code for Information Interchange, uses 7 bits to represent each character in computer memory. The ASCII representation has been adopted as a standard by the U.S. government and is widely accepted.

A unique integer number is assigned to each character. This number called ASCII code of that character is converted into binary for storing in memory. For example, the ASCII code of A is 65, its binary equivalent in 7-bit is 1000001.

Since there are exactly 128 unique combinations of 7 bits, this 7-bit code can represent only128 characters. Another version is ASCII-8, also called extended ASCII, which uses 8 bits for each character, can represent 256 different characters.

For example, the letter A is represented by 01000001, B by 01000010 and so on. ASCII code is enough to represent all of the standard keyboard characters.

It stands for Extended Binary Coded Decimal Interchange Code. This is similar to ASCII and is an 8-bit code used in computers manufactured by International Business Machines (IBM). It is capable of encoding 256 characters.

If ASCII-coded data is to be used in a computer that uses EBCDIC representation, it is necessary to transform ASCII code to EBCDIC code. Similarly, if EBCDIC coded data is to be used in an ASCII computer, EBCDIC code has to be transformed to ASCII.

ISCII stands for Indian Standard Code for Information Interchange or Indian Script Code for Information Interchange. It is an encoding scheme for representing various writing systems of India. ISCII uses 8-bits for data representation.

It was evolved by a standardization committee under the Department of Electronics during 1986-88 and adopted by the Bureau of Indian Standards (BIS). Nowadays ISCII has been replaced by Unicode.

Using 8-bit ASCII we can represent only 256 characters. This cannot represent all characters of written languages of the world and other symbols. Unicode is developed to resolve this problem. It aims to provide a standard character encoding scheme, which is universal and efficient.

It provides a unique number for every character, no matter what the language and platform be. Unicode originally used 16 bits which can represent up to 65,536 characters. It is maintained by a non-profit organization called the Unicode Consortium.

The Consortium first published version 1.0.0 in 1991 and continues to develop standards based on that original work. Nowadays Unicode uses more than 16 bits and hence it can represent more characters. Unicode can represent characters in almost all written languages of the world.

Data Representation of Audio, Image and Video

In most cases, we may have to represent and process data other than numbers and characters. This may include audio data, images, and videos. We can see that like numbers and characters, the audio, image, and video data also carry information.

We will see different file formats for storing sound, image, and video .

Multimedia data such as audio, image, and video are stored in different types of files. The variety of file formats is due to the fact that there are quite a few approaches to compressing the data and a number of different ways of packaging the data.

For example, an image is most popularly stored in Joint Picture Experts Group (JPEG ) file format. An image file consists of two parts – header information and image data. Information such as the name of the file, size, modified data, file format, etc. is stored in the header part.

The intensity value of all pixels is stored in the data part of the file. The data can be stored uncompressed or compressed to reduce the file size. Normally, the image data is stored in compressed form. Let us understand what compression is.

Take a simple example of a pure black image of size 400X400 pixels. We can repeat the information black, black, …, black in all 16,0000 (400X400) pixels. This is the uncompressed form, while in the compressed form black is stored only once and information to repeat it 1,60,000 times is also stored.

Numerous such techniques are used to achieve compression. Depending on the application, images are stored in various file formats such as bitmap file format (BMP), Tagged Image File Format (TIFF), Graphics Interchange Format (GIF), Portable (Public) Network Graphic (PNG).

What we said about the header file information and compression is also applicable for audio and video files. Digital audio data can be stored in different file formats like WAV, MP3, MIDI, AIFF, etc. An audio file describes a format, sometimes referred to as the ‘container format’, for storing digital audio data.

For example, WAV file format typically contains uncompressed sound and MP3 files typically contain compressed audio data. The synthesized music data is stored in MIDI(Musical Instrument Digital Interface) files.

Similarly, video is also stored in different files such as AVI (Audio Video Interleave) – a file format designed to store both audio and video data in a standard package that allows synchronous audio with video playback, MP3, JPEG-2, WMV, etc.

FAQs About Data Representation in Computer

What is number system with example.

Let us discuss some of the number systems. Computer architecture supports the following number of systems: 1. Binary Number System 2. Octal Number System 3. Decimal Number System 4. Hexadecimal Number System

Related posts:

• 10 Types of Computers | History of Computers, Advantages
• What is Microprocessor? Evolution of Microprocessor, Types, Features
• What is operating system? Functions, Types, Types of User Interface
• What is Cloud Computing? Classification, Characteristics, Principles, Types of Cloud Providers
• What is Debugging? Types of Errors
• What are Functions of Operating System? 6 Functions
• What is Flowchart in Programming? Symbols, Advantages, Preparation
• Advantages and Disadvantages of Flowcharts
• What is C++ Programming Language? C++ Character Set, C++ Tokens
• What are C++ Keywords? Set of 59 keywords in C ++
• What are Data Types in C++? Types
• What are Operators in C? Different Types of Operators in C
• What are Expressions in C? Types
• What are Decision Making Statements in C? Types
• Types of Storage Devices, Advantages, Examples

Data Representation 5.3. Numbers

Data representation.

• 5.1. What's the big picture?
• 5.2. Getting started

Understanding the base 10 number system

Representing whole numbers in binary, shorthand for binary numbers - hexadecimal, computers representing numbers in practice, how many bits are used in practice, representing negative numbers in practice.

• 5.5. Images and Colours
• 5.6. Program Instructions
• 5.7. The whole story!
• 5.8. Further reading

In this section, we will look at how computers represent numbers. To begin with, we'll revise how the base 10 number system that we use every day works, and then look at binary , which is base 2. After that, we'll look at some other charactertistics of numbers that computers must deal with, such as negative numbers and numbers with decimal points.

The number system that humans normally use is in base 10 (also known as decimal). It's worth revising quickly, because binary numbers use the same ideas as decimal numbers, just with fewer digits!

In decimal, the value of each digit in a number depends on its place in the number. For example, in $123, the 3 represents $3, whereas the 1 represents $100. Each place value in a number is worth 10 times more than the place value to its right, i.e. there are the "ones", the "tens", the "hundreds", the "thousands" the "ten thousands", the "hundred thousands", the "millions", and so on. Also, there are 10 different digits (0,1,2,3,4,5,6,7,8,9) that can be at each of those place values.

If you were only able to use one digit to represent a number, then the largest number would be 9. After that, you need a second digit, which goes to the left, giving you the next ten numbers (10, 11, 12... 19). It's because we have 10 digits that each one is worth 10 times as much as the one to its right.

You may have encountered different ways of expressing numbers using "expanded form". For example, if you want to write the number 90328 in expanded form you might have written it as:

A more sophisticated way of writing it is:

If you've learnt about exponents, you could write it as:

The key ideas to notice from this are:

• Decimal has 10 digits – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
• A place is the place in the number that a digit is, i.e. ones, tens, hundreds, thousands, and so on. For example, in the number 90328, 3 is in the "hundreds" place, 2 is in the "tens" place, and 9 is in the "ten thousands" place.
• Numbers are made with a sequence of digits.
• The right-most digit is the one that's worth the least (in the "ones" place).
• The left-most digit is the one that's worth the most.
• Because we have 10 digits, the digit at each place is worth 10 times as much as the one immediately to the right of it.

All this probably sounds really obvious, but it is worth thinking about consciously, because binary numbers have the same properties.

As discussed earlier, computers can only store information using bits, which have 2 possible states. This means that they cannot represent base 10 numbers using digits 0 to 9, the way we write down numbers in decimal. Instead, they must represent numbers using just 2 digits – 0 and 1.

Binary works in a very similar way to decimal, even though it might not initially seem that way. Because there are only 2 digits, this means that each digit is 2 times the value of the one immediately to the right.

The base 10 (decimal) system is sometimes called denary, which is more consistent with the name binary for the base 2 system. The word "denary" also refers to the Roman denarius coin, which was worth ten asses (an "as" was a copper or bronze coin). The term "denary" seems to be used mainly in the UK; in the US, Australia and New Zealand the term "decimal" is more common.

The interactive below illustrates how this binary number system represents numbers. Have a play around with it to see what patterns you can see.

Base Calculator

Find the representations of 4, 7, 12, and 57 using the interactive.

What is the largest number you can make with the interactive? What is the smallest? Is there any integer value in between the biggest and the smallest that you can’t make? Are there any numbers with more than one representation? Why/ why not?

• 000000 in binary, 0 in decimal is the smallest number.
• 111111 in binary, 63 in decimal is the largest number.
• All the integer values (0, 1, 2... 63) in the range can be represented (and there is a unique representation for each one). This is exactly the same as decimal!

You have probably noticed from the interactive that when set to 1, the leftmost bit (the "most significant bit") adds 32 to the total, the next adds 16, and then the rest add 8, 4, 2, and 1 respectively. When set to 0, a bit does not add anything to the total. So the idea is to make numbers by adding some or all of 32, 16, 8, 4, 2, and 1 together, and each of those numbers can only be included once.

Choose a number less than 61 (perhaps your house number, your age, a friend's age, or the day of the month you were born on), set all the binary digits to zero, and then start with the left-most digit (32), trying out if it should be zero or one. See if you can find a method for converting the number without too much trial and error. Try different numbers until you find a quick way of doing this.

Figure out the binary representation for 23 without using the interactive? What about 4, 0, and 32? Check all your answers using the interactive to verify they are correct.

Can you figure out a systematic approach to counting in binary? i.e. start with the number 0, then increment it to 1, then 2, then 3, and so on, all the way up to the highest number that can be made with the 7 bits. Try counting from 0 to 16, and see if you can detect a pattern. Hint: Think about how you add 1 to a number in base 10. e.g. how do you work out 7 + 1, 38 + 1, 19 + 1, 99 + 1, 230899999 + 1, etc? Can you apply that same idea to binary?

Using your new knowledge of the binary number system, can you figure out a way to count to higher than 10 using your 10 fingers? What is the highest number you can represent using your 10 fingers? What if you included your 10 toes as well (so you have 20 fingers and toes to count with).

A binary number can be incremented by starting at the right and flipping all consecutive bits until a 1 comes up (which will be on the very first bit half of the time).

Counting on fingers in binary means that you can count to 31 on 5 fingers, and 1023 on 10 fingers. There are a number of videos on YouTube of people counting in binary on their fingers. One twist is to wear white gloves with the numbers 16, 8, 4, 2, 1 on the 5 fingers respectively, which makes it easy to work out the value of having certain fingers raised.

The interactive used exactly 6 bits. In practice, we can use as many or as few bits as we need, just like we do with decimal. For example, with 5 bits, the place values would be 16, 8, 4, 2 and 1, so the largest value is 11111 in binary, or 31 in decimal. Representing 14 with 5 bits would give 01110.

Write representations for the following. If it is not possible to do the representation, put "Impossible".

• Represent 101 with 7 bits
• Represent 28 with 10 bits
• Represent 7 with 3 bits
• Represent 18 with 4 bits
• Represent 28232 with 16 bits

The answers are (spaces are added to make the answers easier to read, but are not required).

• 101 with 7 bits is: 110 0101
• 28 with 10 bits is: 00 0001 1100
• 7 with 3 bits is: 111
• 18 with 4 bits is: Impossible (not enough bits to represent value)
• 28232 with 16 bits is: 0110 1110 0100 1000

An important concept with binary numbers is the range of values that can be represented using a given number of bits. When we have 8 bits the binary numbers start to get useful – they can represent values from 0 to 255, so it is enough to store someone's age, the day of the month, and so on.

Groups of 8 bits are so useful that they have their own name: a byte . Computer memory and disk space are usually divided up into bytes, and bigger values are stored using more than one byte. For example, two bytes (16 bits) are enough to store numbers from 0 to 65,535. Four bytes (32 bits) can store numbers up to 4,294,967,295. You can check these numbers by working out the place values of the bits. Every bit that's added will double the range of the number.

In practice, computers store numbers with either 16, 32, or 64 bits. This is because these are full numbers of bytes (a byte is 8 bits), and makes it easier for computers to know where each number starts and stops.

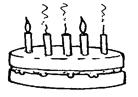
Candles on birthday cakes use the base 1 numbering system, where each place is worth 1 more than the one to its right. For example, the number 3 is 111, and 10 is 1111111111. This can cause problems as you get older – if you've ever seen a cake with 100 candles on it, you'll be aware that it's a serious fire hazard.

Luckily it's possible to use binary notation for birthday candles – each candle is either lit or not lit. For example, if you are 18, the binary notation is 10010, and you need 5 candles (with only two of them lit).

There's a video on using binary notation for counting up to 1023 on your hands, as well as using it for birthday cakes .

Most of the time binary numbers are stored electronically, and we don't need to worry about making sense of them. But sometimes it's useful to be able to write down and share numbers, such as the unique identifier assigned to each digital device (MAC address), or the colours specified in an HTML page.

Writing out long binary numbers is tedious – for example, suppose you need to copy down the 16-bit number 0101001110010001. A widely used shortcut is to break the number up into 4-bit groups (in this case, 0101 0011 1001 0001), and then write down the digit that each group represents (giving 5391). There's just one small problem: each group of 4 bits can go up to 1111, which is 15, and the digits only go up to 9.

The solution is simple: we introduce symbols for the digits from 1010 (10) to 1111 (15), which are just the letters A to F. So, for example, the 16-bit binary number 1011 1000 1110 0001 can be written more concisely as B8E1. The "B" represents the binary 1011, which is the decimal number 11, and the E represents binary 1110, which is decimal 14.

Because we now have 16 digits, this representation is base 16, and known as hexadecimal (or hex for short). Converting between binary and hexadecimal is very simple, and that's why hexadecimal is a very common way of writing down large binary numbers.

Here's a full table of all the 4-bit numbers and their hexadecimal digit equivalent:

For example, the largest 8-bit binary number is 11111111. This can be written as FF in hexadecimal. Both of those representations mean 255 in our conventional decimal system (you can check that by converting the binary number to decimal).

Which notation you use will depend on the situation; binary numbers represent what is actually stored, but can be confusing to read and write; hexadecimal numbers are a good shorthand of the binary; and decimal numbers are used if you're trying to understand the meaning of the number or doing normal math. All three are widely used in computer science.

It is important to remember though, that computers only represent numbers using binary. They cannot represent numbers directly in decimal or hexadecimal.

A common place that numbers are stored on computers is in spreadsheets or databases. These can be entered either through a spreadsheet program or database program, through a program you or somebody else wrote, or through additional hardware such as sensors, collecting data such as temperatures, air pressure, or ground shaking.

Some of the things that we might think of as numbers, such as the telephone number (03) 555-1234, aren't actually stored as numbers, as they contain important characters (like dashes and spaces) as well as the leading 0 which would be lost if it was stored as a number (the above number would come out as 35551234, which isn't quite right). These are stored as text , which is discussed in the next section.

On the other hand, things that don't look like a number (such as "30 January 2014") are often stored using a value that is converted to a format that is meaningful to the reader (try typing two dates into Excel, and then subtract one from the other – the result is a useful number). In the underlying representation, a number is used. Program code is used to translate the underlying representation into a meaningful date on the user interface.

The difference between two dates in Excel is the number of days between them; the date itself (as in many systems) is stored as the amount of time elapsed since a fixed date (such as 1 January 1900). You can test this by typing a date like "1 January 1850" – chances are that it won't be formatted as a normal date. Likewise, a date sufficiently in the future may behave strangely due to the limited number of bits available to store the date.

Numbers are used to store things as diverse as dates, student marks, prices, statistics, scientific readings, sizes and dimensions of graphics.

The following issues need to be considered when storing numbers on a computer:

• What range of numbers should be able to be represented?
• How do we handle negative numbers?
• How do we handle decimal points or fractions?

In practice, we need to allocate a fixed number of bits to a number, before we know how big the number is. This is often 32 bits or 64 bits, although can be set to 16 bits, or even 128 bits, if needed. This is because a computer has no way of knowing where a number starts and ends, otherwise.

Any system that stores numbers needs to make a compromise between the number of bits allocated to store the number, and the range of values that can be stored.

In some systems (like the Java and C programming languages and databases) it's possible to specify how accurately numbers should be stored; in others it is fixed in advance (such as in spreadsheets).

Some are able to work with arbitrarily large numbers by increasing the space used to store them as necessary (e.g. integers in the Python programming language). However, it is likely that these are still working with a multiple of 32 bits (e.g. 64 bits, 96 bits, 128 bits, 160 bits, etc). Once the number is too big to fit in 32 bits, the computer would reallocate it to have up to 64 bits.

In some programming languages there isn't a check for when a number gets too big (overflows). For example, if you have an 8-bit number using two's complement, then 01111111 is the largest number (127), and if you add one without checking, it will change to 10000000, which happens to be the number -128. (Don't worry about two's complement too much, it's covered later in this section.) This can cause serious problems if not checked for, and is behind a variant of the Y2K problem, called the Year 2038 problem , involving a 32-bit number overflowing for dates on Tuesday, 19 January 2038.

On tiny computers, such as those embedded inside your car, washing machine, or a tiny sensor that is barely larger than a grain of sand, we might need to specify more precisely how big a number needs to be. While computers prefer to work with chunks of 32 bits, we could write a program (as an example for an earthquake sensor) that knows the first 7 bits are the lattitude, the next 7 bits are the longitude, the next 10 bits are the depth, and the last 8 bits are the amount of force.

Even on standard computers, it is important to think carefully about the number of bits you will need. For example, if you have a field in your database that could be either "0", "1", "2", or "3" (perhaps representing the four bases that can occur in a DNA sequence), and you used a 64 bit number for every one, that will add up as your database grows. If you have 10,000,000 items in your database, you will have wasted 62 bits for each one (only 2 bits is needed to represent the 4 numbers in the example), a total of 620,000,000 bits, which is around 74 MB. If you are doing this a lot in your database, that will really add up – human DNA has about 3 billion base pairs in it, so it's incredibly wasteful to use more than 2 bits for each one.

And for applications such as Google Maps, which are storing an astronomical amount of data, wasting space is not an option at all!

It is really useful to know roughly how many bits you will need to represent a certain value. Have a think about the following scenarios, and choose the best number of bits out of the options given. You want to ensure that the largest possible number will fit within the number of bits, but you also want to ensure that you are not wasting space.

• Storing the day of the week - a) 1 bit - b) 4 bits - c) 8 bits - d) 32 bits
• Storing the number of people in the world - a) 16 bits - b) 32 bits - c) 64 bits - d) 128 bits
• Storing the number of roads in New Zealand - a) 16 bits - b) 32 bits - c) 64 bits - d) 128 bits
• Storing the number of stars in the universe - a) 16 bits - b) 32 bits - c) 64 bits - d) 128 bits
• b (actually, 3 bits is enough as it gives 8 values, but amounts that fit evenly into 8-bit bytes are easier to work with)
• c (32 bits is slightly too small, so you will need 64 bits)
• b (This is a challenging question, but one a database designer would have to think about. There's about 94,000 km of roads in New Zealand, so if the average length of a road was 1km, there would be too many roads for 16 bits. Either way, 32 bits would be a safe bet.)
• d (Even 64 bits is not enough, but 128 bits is plenty! Remember that 128 bits isn't twice the range of 64 bits.)

The binary number representation we have looked at so far allows us to represent positive numbers only. In practice, we will want to be able to represent negative numbers as well, such as when the balance of an account goes to a negative amount, or the temperature falls below zero. In our normal representation of base 10 numbers, we represent negative numbers by putting a minus sign in front of the number. But in binary, is it this simple?

We will look at two possible approaches: Adding a simple sign bit, much like we do for decimal, and then a more useful system called two's complement.

Using a simple sign bit

On a computer we don’t have minus signs for numbers (it doesn't work very well to use the text based one when representing a number because you can't do arithmetic on characters), but we can do it by allocating one extra bit, called a sign bit, to represent the minus sign. Just like with decimal numbers, we put the negative indicator on the left of the number — when the sign bit is set to "0", that means the number is positive and when the sign bit is set to "1", the number is negative (just as if there were a minus sign in front of it).

For example, if we wanted to represent the number 41 using 7 bits along with an additional bit that is the sign bit (to give a total of 8 bits), we would represent it by 00101001 . The first bit is a 0, meaning the number is positive, then the remaining 7 bits give 41 , meaning the number is +41 . If we wanted to make -59 , this would be 10111011 . The first bit is a 1, meaning the number is negative, and then the remaining 7 bits represent 59 , meaning the number is -59 .

Using 8 bits as described above (one for the sign, and 7 for the actual number), what would be the binary representations for 1, -1, -8, 34, -37, -88, and 102?

The spaces are not necessary, but are added to make reading the binary numbers easier

• 1 is 0000 0001
• -1 is 1000 0001
• -8 is 1000 1000
• 34 is 0010 0010
• -37 is 1010 0101
• -88 is 1101 1000
• 102 is 0110 0110

Going the other way is just as easy. If we have the binary number 10010111 , we know it is negative because the first digit is a 1. The number part is the next 7 bits 0010111 , which is 23 . This means the number is -23 .

What would the decimal values be for the following, assuming that the first bit is a sign bit?

• 00010011 is 19
• 10000110 is -6
• 10100011 is -35
• 01111111 is 127
• 11111111 is -127

But what about 10000000? That converts to -0 . And 00000000 is +0 . Since -0 and +0 are both just 0, it is very strange to have two different representations for the same number.

This is one of the reasons that we don't use a simple sign bit in practice. Instead, computers usually use a more sophisticated representation for negative binary numbers called two's complement .

Two's complement

There's an alternative representation called two's complement , which avoids having two representations for 0, and more importantly, makes it easier to do arithmetic with negative numbers.

Representing positive numbers with two's complement

Representing positive numbers is the same as the method you have already learnt. Using 8 bits ,the leftmost bit is a zero and the other 7 bits are the usual binary representation of the number; for example, 1 would be 00000001 , and 50 would be 00110010 .

Representing negative numbers with two's complement

This is where things get more interesting. In order to convert a negative number to its two's complement representation, use the following process. 1. Convert the number to binary (don't use a sign bit, and pretend it is a positive number). 2. Invert all the digits (i.e. change 0's to 1's and 1's to 0's). 3. Add 1 to the result (Adding 1 is easy in binary; you could do it by converting to decimal first, but think carefully about what happens when a binary number is incremented by 1 by trying a few; there are more hints in the panel below).

For example, assume we want to convert -118 to its two's complement representation. We would use the process as follows. 1. The binary number for 118 is 01110110 . 2. 01110110 with the digits inverted is 10001001 . 3. 10001001 + 1 is 10001010 .

Therefore, the two's complement representation for -118 is 10001010 .

The rule for adding one to a binary number is pretty simple, so we'll let you figure it out for yourself. First, if a binary number ends with a 0 (e.g. 1101010), how would the number change if you replace the last 0 with a 1? Now, if it ends with 01, how much would it increase if you change the 01 to 10? What about ending with 011? 011111?

The method for adding is so simple that it's easy to build computer hardware to do it very quickly.

What would be the two's complement representation for the following numbers, using 8 bits ? Follow the process given in this section, and remember that you do not need to do anything special for positive numbers.

• 19 in binary is 0001 0011 , which is the two's complement for a positive number.
• For -19, we take the binary of the positive, which is 0001 0011 (above), invert it to 1110 1100, and add 1, giving a representation of 1110 1101 .
• 107 in binary is 0110 1011 , which is the two's complement for a positive number.
• For -107, we take the binary of the positive, which is 0110 1011 (above), invert it to 1001 0100, and add 1, giving a representation of 1001 0101 .
• For -92, we take the binary of the positive, which is 0101 1100, invert it to 1010 0011, and add 1, giving a representation of 1010 0100 . (If you have this incorrect, double check that you incremented by 1 correctly).

Converting a two's complement number back to decimal

In order to reverse the process, we need to know whether the number we are looking at is positive or negative. For positive numbers, we can simply convert the binary number back to decimal. But for negative numbers, we first need to convert it back to a normal binary number.

So how do we know if the number is positive or negative? It turns out (for reasons you will understand later in this section) that two's complement numbers that are negative always start in a 1, and positive numbers always start in a 0. Have a look back at the previous examples to double check this.

So, if the number starts with a 1, use the following process to convert the number back to a negative decimal number.

• Subtract 1 from the number.
• Invert all the digits.
• Convert the resulting binary number to decimal.
• Add a minus sign in front of it.

So if we needed to convert 11100010 back to decimal, we would do the following.

• Subtract 1 from 11100010 , giving 11100001 .
• Invert all the digits, giving 00011110 .
• Convert 00011110 to a binary number, giving 30 .
• Add a negative sign, giving -30 .

Convert the following two's complement numbers to decimal.

• 10001100 -> (-1) 10001011 -> (inverted) 01110100 -> (to decimal) 116 -> (negative sign added) -116
• 10111111 -> (-1) 10111110 -> (inverted) 01000001 -> (to decimal) 65 -> (negative sign added) -65

How many numbers can be represented using two's complement?

While it might initially seem that there is no bit allocated as the sign bit, the left-most bit behaves like one. With 8 bits, you can still only make 256 possible patterns of 0's and 1's. If you attempted to use 8 bits to represent positive numbers up to 255, and negative numbers down to -255, you would quickly realise that some numbers were mapped onto the same pattern of bits. Obviously, this will make it impossible to know what number is actually being represented!

In practice, numbers within the following ranges can be represented. Unsigned Range is how many numbers you can represent if you only allow positive numbers (no sign is needed), and two's complement Range is how many numbers you can represent if you require both positive and negative numbers. You can work these out because the range of 8-bit values if they are stored using unsigned numbers will be from 00000000 to 11111111 (i.e. 0 to 255 in decimal), while the signed two's complement range is from 10000000 (the lowest number, -128 in decimal) to 01111111 (the highest number, 127 in decimal). This might seem a bit weird, but it works out really well because normal binary addition can be used if you use this representation even if you're adding a negative number.

Adding negative binary numbers

Before adding negative binary numbers, we'll look at adding positive numbers. It's basically the same as the addition methods used on decimal numbers, except the rules are way simpler because there are only two different digits that you might add!

You've probably learnt about column addition. For example, the following column addition would be used to do 128 + 255 .

When you go to add 5 + 8, the result is higher than 9, so you put the 3 in the one's column, and carry the 1 to the 10's column. Binary addition works in exactly the same way.

Adding positive binary numbers

If you wanted to add two positive binary numbers, such as 00001111 and 11001110 , you would follow a similar process to the column addition. You only need to know 0+0, 0+1, 1+0, and 1+1, and 1+1+1. The first three are just what you might expect. Adding 1+1 causes a carry digit, since in binary 1+1 = 10, which translates to "0, carry 1" when doing column addition. The last one, 1+1+1 adds up to 11 in binary, which we can express as "1, carry 1". For our two example numbers, the addition works like this:

Remember that the digits can be only 1 or 0. So you will need to carry a 1 to the next column if the total you get for a column is (decimal) 2 or 3.

Adding negative numbers with a simple sign bit

With negative numbers using sign bits like we did before, this does not work. If you wanted to add +11 (01011) and -7 (10111) , you would expect to get an answer of +4 (00100) .

Which is -2 .

One way we could solve the problem is to use column subtraction instead. But this would require giving the computer a hardware circuit which could do this. Luckily this is unnecessary, because addition with negative numbers works automatically using two's complement!

Adding negative numbers with two's complement

For the above addition (+11 + -7), we can start by converting the numbers to their 5-bit two's complement form. Because 01011 (+11) is a positive number, it does not need to be changed. But for the negative number, 00111 (-7) (sign bit from before removed as we don't use it for two's complement), we need to invert the digits and then add 1, giving 11001 .

Adding these two numbers works like this:

Any extra bits to the left (beyond what we are using, in this case 5 bits) have been truncated. This leaves 00100 , which is 4 , like we were expecting.

We can also use this for subtraction. If we are subtracting a positive number from a positive number, we would need to convert the number we are subtracting to a negative number. Then we should add the two numbers. This is the same as for decimal numbers, for example 5 - 2 = 3 is the same as 5 + (-2) = 3.

This property of two's complement is very useful. It means that positive numbers and negative numbers can be handled by the same computer circuit, and addition and subtraction can be treated as the same operation.

The idea of using a "complementary" number to change subtraction to addition can be seen by doing the same in decimal. The complement of a decimal digit is the digit that adds up to 10; for example, the complement of 4 is 6, and the complement of 8 is 2. (The word "complement" comes from the root "complete" – it completes it to a nice round number.)

Subtracting 2 from 6 is the same as adding the complement, and ignoring the extra 1 digit on the left. The complement of 2 is 8, so we add 8 to 6, giving (1)4.

For larger numbers (such as subtracting the two 3-digit numbers 255 - 128), the complement is the number that adds up to the next power of 10 i.e. 1000-128 = 872. Check that adding 872 to 255 produces (almost) the same result as subtracting 128.

Working out complements in binary is way easier because there are only two digits to work with, but working them out in decimal may help you to understand what is going on.

Using sign bits vs using two's complement

We have now looked at two different ways of representing negative numbers on a computer. In practice, a simple sign bit is rarely used, because of having two different representations of zero, and requiring a different computer circuit to handle negative and positive numbers, and to do addition and subtraction.

Two's complement is widely used, because it only has one representation for zero, and it allows positive numbers and negative numbers to be treated in the same way, and addition and subtraction to be treated as one operation.

There are other systems such as "One's Complement" and "Excess-k", but two's complement is by far the most widely used in practice.

Computer representation of numbers

Integer representation.

You are in charge of the US Census for 2000. You must design computers to keep track of people. How many bytes should you devote to the population count?

Floating point representations

You are given a single byte, 8 bits, for storing signed, floating-point numbers. You choose the following system: 1 bit for sign, 3 bits for a signed exponent, 4 bits for mantissa Answer the following questions: What is the largest positive value you can express? What is the smallest positive value you can express? What is the "average" spacing between values in your system? That is, what is the total range of positive values, divided by the number of different values inside that range? How many different values does your system have between the numbers 5.1 and 6.8?

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Computers and the Internet

Course: computers and the internet   >   unit 1, how do computers represent data.

• Binary & data
• Bits (binary digits)

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Representing Numbers in Computers

The smallest unit of information that can be stored by a computer is a binary digit (usually shortened to "bit"). Its value is usually held in memory as an electrical charge stored in a capacitor. Modern memory chips contain millions of these tiny capacitors, each of which is capable of storing exactly one bit of information. A single bit can have one of two values at any given time - one or zero . As we shall see, in order to represent a number greater than one, we will have to use several bits.

Fixed-point numbers

Floating-point numbers, one's complement.

• Two’s complement
• Binary-Coded Decimal (BCD)

BCD addition

Bcd subtraction.

Generally speaking, single bits are used only for storing Boolean values (true or false). In most programming languages, true equates to one , while false equates to zero . The smallest unit of data that can be addressed in computer memory is the byte . The definition of the byte has varied over the years but it is now generally considered to be a group of eight bits, and can be used to represent alpha-numeric and non-printing characters, unsigned integer (whole number) values from 0 to 255 , or signed integer values from -127 to +127 .

A byte usually consists of eight bits

Some texts refer to a group of eight bits as an octet to avoid any possible ambiguity. Because the hexadecimal number system consists of sixteen digits, each of which can be specified using just four bits, it is sometimes useful to consider groupings of four bits as a unit. Such a grouping is often referred to as a nibble (which undoubtedly proves that computer scientists have a sense of humour after all!).

The number of bits that can be processed by a CPU in a single machine operation is dependent upon the number of bits it can store in its internal registers. In the early days of computing this was a relatively small number (four or eight bits). At some point, therefore, the size of the processor's register coincided with the size of a byte. For many years now, however, this has not been the case. As CPU architecture has evolved, we have seen the size of registers double and re-double. Most processors now have either 32-bit or 64-bit registers that can hold four or eight bytes of data respectively.

A modern CPU has a 64-bit architecture

The unit of data that can be processed in a single operation by a machine-code instruction is called a word . A word can be viewed as a 32-bit or 64-bit binary number. The range of values that can be represented by a word is therefore dependent on microprocessor architecture, and will determine the size of the memory space that can be addressed.

As of 2010, practically all personal computers are capable of processing 64-bits of data, although they are frequently used in 32-bit mode in order to provide support for existing software. Keep in mind however that many embedded systems still use microcontroller chips that have eight or sixteen-bit registers.

Integers are whole numbers. The range of values that can be stored as an integer depends on whether or not the number is signed (i.e. positive or negative), and how much memory is allocated for it in memory. Programming languages can generally represent integers that are signed or unsigned, and of different sizes.

A single byte can represent unsigned numbers ranging in value from 0 to 255 , or signed integers ranging from -128 to +127 . If two bytes are used, unsigned numbers from 0 to 65,535 or signed numbers from -32,768 to 32,767 can be stored. Much larger numbers can be represented if more bytes are made available.

For signed numbers, one bit is used to store the sign ( + or - ) of the number, so the absolute value of the biggest number that can be stored is only half that for unsigned numbers. The number of bits used to represent an integer value will equal the number of bytes multiplied by eight. An integer represented by n bits can represent 2 n numbers.

The magnitude of a four-byte integer can thus be anything up to 2  (4×8) or 2  32 which means it can hold an unsigned value of up to 4,294,967,296 (a tad over two billion). Negative numbers can be represented in several different ways in binary number systems, although the most commonly used method is two's complement (the subject of two's complement is dealt with below).

A fixed-point number is used to represent a real number (one that has a fractional part) using a fixed number of digits after the radix point. The radix point is called the decimal point for real numbers to base ten. In binary number systems it would be called the binary point . Fixed-point numbers are sometimes used where the processor employed does not have a floating-point unit (FPU), which is often the case in low-cost microcontrollers.

Fixed point fractional numbers are usually represented by integer values that are scaled by an appropriate factor (the exponent ). For example, the real number 1.234 could be represented by the integer value 1234 , with a scaling factor of  1 / 1000  (or 10  -3 ), while the number 1,234,000 could also be represented by the integer value 1234 but using a scaling factor of 1000 ( 10  3 ).

The difference between fixed-point and floating-point representation of real numbers is that the scaling factor remains the same for all values represented by a particular fixed-point data type. The scaling factor used will (usually) be a power of ten for denary (base ten) numbers or a power of two for binary numbers.

The maximum and minimum values that can be represented by a fixed-point data type will depend on the maximum and minimum values that can be represented by the underlying integer data type, and the scaling factor.

Arithmetic operations on fixed-point numbers can produce answers that cannot be accurately represented using the number of places available either before or after the radix point. In such cases, the answer will be rounded or truncated. The options are either to keep the same number format for the answer and accept that there will be some loss of accuracy, or to convert the result to a more appropriate data type to preserve accuracy.

In the first approach, the number of digits before and after the radix point remains the same for the result of an operation. If digits are lost from the fractional part of the result, there will be an associated loss of precision that may be acceptable in many cases. If digits are lost from the integer part of the result however, the result will be fundamentally incorrect.

When writing programs for control systems that will be implemented on microprocessors, it is essential to understand the limitations of the microprocessor being used in terms of the maximum size of the integer values it can store. This will usually depend on the size of its internal registers.

Floating-point numbers are somewhat more complicated to deal with because the radix point does not occupy a fixed position (i.e. it can "float" to the left or right within the representation of a real number depending on the number's magnitude). In most commonly used encodings, a floating-point value is stored as three separate components – the significand , the exponent , and the sign . A 32-bit floating-point number is typically made up as follows:

• Significand - 23 bits
• Exponent - 8 bits
• Sign - 1 bit

The significand represents the significant digits of the number itself, while the exponent essentially represents the position occupied within those digits of the decimal (or binary) point. When a floating-point value is stored in memory, it is first normalised . This means moving the decimal point to the left until it is immediately on the right of the most significant (left-most) digit. The number of places that the decimal point must be moved in order to achieve this is the exponent.

As an example, take the real number 1234.56 (which has a significand of 123456 ). In order to normalise the number, we need to move the radix point (in this case, a decimal point) three places to the left, resulting in a normalised value of 1.23456 and an exponent of 3 . Because we are looking at a denary (base ten) number, we can now write the number as 1.23456 × 10  3 .

Binary real numbers can be dealt with in exactly the same way, except that the exponent will be applied to a number base of two. Note however that fractional values such as  1 / 5  ( 0.2 ) that can be represented exactly in base ten cannot be exactly represented in base two.

From the above, it should be evident that the maximum number of digits that can be used to represent any real number in a given format will be fixed. It follows that for any given number, the precision of its representation will depend on the number of digits required to represent it exactly. If the number of digits required is less than or equal to the number of digits available in a given representation, there will be no loss of precision. If the number of digits required is greater than the number available, there will inevitably be some loss of precision.

Of course, for values that do not have an exact representation in a given number base precision will be limited in any case. The fractional value  1 / 3  , for example, cannot be exactly represented in a denary number system, no matter how many digits are used after the decimal point (although as more digits are added, the value stored will more closely approach the actual value). A number that cannot be represented exactly in a number base regardless of the number of digits used is said to be non-terminating .

The main advantage floating-point numbers have over fixed-point numbers is that they can represent a much greater range of values. If we use a fixed-point format with two significant digits after the decimal point, for example, the significand 1234567 could represent the values 12,345.67 , 1,234.56 , 123.45 , 12.34 and so on. A floating-point number with the same significand could represent values such as 1.234567 , 123,456.7 , 0.00001234567 , 1,234,567,000,000 and so on.

The down side is that the floating-point format requires more bits to store the exponent part of the number, so floating-point numbers that occupy the same space as a fixed-point data type achieve a greater range at the expense of some loss of precision. Generally speaking, the larger the range of values we wish to represent, the more bits are needed to store numbers in that range.

Because the number of bits available for both the significand and the exponent will be fixed for a given real number data type, programming languages tend to offer floating-point data types of different sizes (and hence precision) so that the programmer can select the type most appropriate for the intended purpose of a variable. In this way, memory can be used more economically than if there were a single "one size fits all" real number data type. Floating-point values are usually represented using either 32 bits ( single precision ) or 64 bits ( double precision ).

As we said earlier, the significand is stored as an integer having a fixed number of digits, with an implied radix point to the immediate right of the most significant digit. In order to derive the real number value being stored, the significand must be multiplied by the base raised to the power of the exponent. This will effectively move the radix point from its implied position by the number of places given by the exponent.

If the exponent is positive, the radix point moves to the right. If the exponent is negative, it moves to the left. Using a denary example, the number 12345.67 would be normalised to 1.234567 . In order to restore the number to its original value, the normalised value would have to be multiplied by 10  4 . Note that the computer representation of binary floating-point numbers is standardised in IEEE 754-2008 - the IEEE Standard for Floating-Point Arithmetic.

A computer uses a fixed number of bits to store each of the common data types. For example, a byte (8 bits) is commonly used to represent alphanumeric characters, unsigned integer values from 0 to 255 , or signed integer values from -127 to +127 .

For signed integer data types, the range of values that can be represented is only half that for unsigned integer data types because the most significant bit is used to signify whether the number is positive ( 0 ) or negative ( 1 ), leaving one less bit available to represent the absolute value of the number.

The range of signed 4-bit integers that can be represented using this system (known as sign and magnitude ) is shown in the table below, and illustrates how the system works. Note that there are two possible representations for zero ( 0000 2  = +0 10  and 1000 2  = -0 10  ).

Signed integers can be represented using a number of alternative systems, one of which is called one's complement . Using one's complement, the most significant bit is again used to indicate the sign ( 0 = positive, 1 = negative), and positive numbers are represented in the normal way (see above).

To change the sign of a positive number (i.e. to negate it) using one's complement however, all of the bits are inverted (or "flipped"). In other words, all the ones are replaced with zeros, and all the zeros are replaced with ones. The following binary numbers are the 8-bit one's complement representation of 12 10 and -12 10 , respectively:

12 10   =  0001100 2 -12 10   =  1110011 2

For those familiar with Boolean logic, the one's complement of any binary number is the equivalent of carrying out a bitwise NOT operation on it and it should be fairly obvious that the one's complement of a negative one's complement number is its positive counterpart.

The 8-bit binary representation of zero using one's complement can take one of two forms - 00000000 2 (+0 10 ) or 11111111 2 (−0 10 ) , and the range of values that can be represented using 8 bits is -127 10 to +127 10 . One of the benefits of using one's complement is that addition and subtraction can both be carried out using binary addition, with end-around carry (this simply means that if there is a carry of one bit into the bit position to the left of the most significant bit as a result of the addition, the bit is added back to the least significant bit).

To subtract one binary number x from another binary number y using one's complement, simply add y to the one's complement of x . The two examples below illustrate the principle.

118 10 – 85 10   =  01110110 2 – 01010101 2   =  33 10   =  00100001 2

   01110110 +  10101010     (one's complement of 01010101 )    -------- = 100100000     (result of standard binary addition) =  00100001     (overflow bit is added back to LSB)

106 10 + -79 10 (01101010 2 – 10110000 2 ) = 27 10 (00011011 2 )

   01101010 +  10110000     (one's complement of 01001111 )    -------- = 100011010     (result of standard binary addition) =  00011011     (overflow bit is added back to LSB)

Two's Complement

Because of the limitations of one's complement when carrying out arithmetic operations such as multiplication and division, the most commonly used way of representing signed integers on computers is to use two's complement , because it allows the logic that handles arithmetic functions to be implemented more easily in hardware.

The two's complement of a binary number is the value obtained by subtracting the number from a large power of two (specifically, from 2 n for an n -bit number). As with one's complement, the most significant bit is used to indicate the sign ( 0 = positive, 1 = negative), and positive numbers are represented in the same way. To negate a positive number, its two's complement is used.

Taking the unsigned number 3 10 as an example, this would be represented as a positive 8-bit two's complement binary number as 00000011 2 . The value of 2 8 expressed in standard binary format is 100000000 . In order to find the two's complement of +3 , therefore, we would carry out the following arithmetic operation:

 100000000 - 00000011   -------- = 11111101

Negative binary numbers can thus be represented using the two's complement of their absolute value. The absolute value of the largest negative number that can be represented with a given number of bits is always one more than that of the largest positive number that can be represented using the same number of bits. Thus, a two's complement 8-bit binary number can represent signed integer values from −128 to +127 (note that the two's complement of -128 is -128 ).

For similar reasons, zero has only a single representation in a two's complement binary system, since the two's complement of zero is zero. It is worth noting that the two's complement of a binary number can also be obtained by adding one to the one's complement of that number.

Putting this in simple terms, you can get the two's complement of a number simply by inverting all the bits (i.e. changing ones to zeros, and zeros to ones) to get the one's complement, and adding one to the result (any resulting carry past the most significant bit is ignored). The range of signed 4-bit integers that can be represented using two's complement is shown in the table below.

Like one's complement, two's complement allows an addition operation to be used to carry out both addition and subtraction. To subtract one binary number x from another binary number y using two's complement, simply add y to the two's complement of x (any carry past the most significant bit is simply ignored). The two examples below illustrate the principle.

118 10 - 85 10 (01110110 2 – 01010101 2 )  =  33 10 (00100001 2 )

  01110110 + 10101011     (two's complement of 01010101 )   -------- = 00100001     (result of standard binary addition, ignoring overflow)

106 10 + -79 10 (01101010 2 + 10110000 2 )  =  27 10 (00011011 2 )

  01101010 + 10110001     (two's complement of 01001111 )   -------- = 00011011     (result of standard binary addition, ignoring overflow)

Note that although binary arithmetic (addition, subtraction, multiplication and division) is simplified by the use of the two's complement representation of signed binary values, the problem remains that an arithmetic operation involving numbers having a fixed number of bits may well produce a result that requires more than the number of bits provided.

The addition of the 8-bit signed integers 117 10 and 96 10 , for example, would produce the result 213 10 . This result is outside the range of values that can be stored as an 8-bit signed binary integer, regardless of the type of representation used ( sign and magnitude , one's complement , or two's complement ). For this reason, computers will carry out checks to determine whether the result of an arithmetic operation will result in an overflow, and as a result will often need to promote a value from one data type to another (e.g. from integer to long integer ).

When converting an 8-bit two's complement number to a 16-bit two's complement number, a process of sign extension occurs, in which the sign bit (the most significant bit of the original 8-bit binary number) is repeated in every bit position to the left of it in the new 16-bit version. The following examples illustrate this:

01010101 2 (+85 10 ) = 00000000 01010101 2 (as a 16-bit number)

00111011 2 (-59 10 ) = 11111111 10101011 2 (as a 16-bit number)

Finally, it is worth noting that binary multiplication is also relatively straightforward in a two's complement system. For example, a bitwise multiplication of 11110100 2 ( -12 10 ) and 00001000 2 ( +8 10 ) gives the result 11110100000 2 .

Since we are dealing with 8-bit numbers, we can drop the leftmost three bits, leaving 10100000 2 . Since the most significant bit is 1, we know the result has a negative value. The two's complement of 10100000 2 is 01100000 2 , or 96 10 , so the result represents -96 10 , which is the correct result of multiplying -12 10 and +8 10 .

Binary-Coded Decimal

In electronic control systems, binary-coded decimal (BCD) is a method for representing decimal numbers in which each decimal digit is represented by a sequence of binary digits. This makes it relatively easy for the system to convert the numeric representation for printing or display purposes, and speeds up decimal calculations. The main disadvantage is that representing decimal numbers in this way takes up more space in memory than using a more conventional binary representation.

The circuitry required to carry out calculations also tends to be more complex. The decimal digits 0-9 are each represented using four bits. Additional bit combinations may be used to represent sign values ( + or - ) or other values (e.g. overflow or error conditions). The table below shows the standard BCD encodings for the decimal digits 0-9 . Note that values greater than 1001 ( 1010 , 1011 , 1100 , 1101 , 1110 , or 1111 ) are not valid BCD decimal values.

The BCD encoding for the number 123 would therefore be:

0001 0010 0011

As opposed to the normal binary representation:

Computers usually store data in blocks of 8 bits (called bytes ). Two main methods of storing BCD digits are used. In the first method (called zoned BCD ), each 4-bit BCD representation of a decimal digit is stored in the right-most four bits of a byte. The left-most four bits are all set to zero, or all set to one in systems such as mainframe computers that use Extended Binary Coded Decimal Interchange Code (EBCDIC), or to 0011 (in systems that use the American Standard Code for Information Interchange (ASCII).

In the second form of representation, two BCD encoded decimal digits are stored in a single byte. Displaying a BCD-encoded number is relatively straightforward for hardware, because each of the numeric characters is mapped to a distinct bit pattern consisting of four binary digits. The control circuitry required to display each number is therefore relatively straightforward since no arithmetic conversion is required.

Another variation on BCD encoding called packed BCD uses each byte of a multi-byte word to store two BCD-encoded decimal digits except the lowest byte. In this byte, the upper four bits are used to store a BCD-encoded decimal digit, but the lowest four bits are used to store the sign value (most commonly 1100 for ' + ' and 1101 for ' - '). A 32-bit word can thus hold a 7-digit signed decimal number using binary coded decimal encoding. The number -1,234,567 would therefore be represented as follows:

0001 0010 0011 0100 0101 0110 0111 1101

The same sign values can be used with zoned BCD to represent signed numbers. The left-most four bits of the least significant byte are used to represent the sign of the number. For an EBCDIC representation of -123 , therefore, the binary pattern used would be as follows:

1111 0001 1111 0010 1101 0011

Unpacked BCD numbers can be added together in the same way that other binary numbers are added together, with the result being put into the appropriate binary format afterwards. If the result of adding two BCD numbers is greater than 9 10 ( 1001 ), however, the result will be invalid and must be corrected by adding 6 10 ( 0110 ). Take the example of adding 7 and 8 :

  0000 0111 + 0000 1000   --------- = 0000 1111

The answer derived is OK for normal binary addition ( 1111 2 = 15 10 ) but results in an invalid BCD representation. In order to rectify this, we need to add 6 (0110) to the result, as follows (note that the number being added must also be in the unpacked format):

  0000 1111 + 0000 0110   --------- = 0001 0101

We now have two BCD values represented, 1 and 5 . This is the correct BCD representation of 15 (the correct result of adding 7 and 8 ). In order to correctly represent this number in the unpacked BCD format, however, we need to shift the left-most four bits of the answer into a higher-order byte, as shown below.

0000 0001 0000 0101 = 15 10

Adding together groups of BCD values is trickier, but basically involves adding each set of BCD encoded values from right to left, and carrying the second digit to the next highest order byte (remembering of course to correct for invalid BCD results before doing so). The following example, in which we will add 97 to 48 , illustrates the principle (note that the BCD-encoded values that will appear in the final encoding are highlighted at each stage):

Add the first set of values:

The result is an invalid BCD value, so add 0110 :

Add the second set of values (plus the 1 carried from the first addition):

  0000 1001 + 0000 0100 + 0000 0001   --------- = 0000 1110

This result of this addition is also an invalid BCD value, so add 0110 :

  0000 1110 + 0000 0110   --------- = 0001 0100

The 1 will be carried into the next highest order byte. The overall result of the addition is shown below (note that the same method for addition can also be applied to packed BCD - just remember that each byte contains two BCD-encoded decimal digits rather than one).

0000 0001 0000 0100 0000 0101 = 145 10

Binary subtraction can be carried out on both packed and unpacked BCD-encoded numbers in the same way that it can for numbers that use a standard binary representation. Note that, as with addition, subtraction can result in an invalid BCD value. It can also give an erroneous answer if the subtraction operation results in a borrow (from the next highest BCD-encoded value).

If either of these situations occurs, an adjustment is needed to produce a correct result. For subtraction, we need to subtract 6 ( 0110 ) from the invalid or erroneous BCD value. Some examples will illustrate the point (we will use packed BCD values for the purposes of this exercise). First, a straightforward example that requires no corrections would be to subtract 12 from 37 :

  0011 0111 - 0001 0010   --------- = 0010 0101

For the next example, we will subtract 19 from 65 :

  0110 0101 - 0001 1001   --------- = 0100 1100

Since the right-most BCD value is invalid, we need to subtract 6 ( 0110 ):

  0100 1100 - 0000 0110   --------- = 0100 0110

The adjustment gives us the correct answer:

0100 0110 = 46 10

For the final example we will subtract 18 from 41 :

  0100 0001 - 0001 1000   --------- = 0010 1001

Since we had to borrow from the left most BCD value when subtracting, the right most BCD value in the result is erroneous and we again need to subtract 6 ( 0110 ):

  0010 1001 - 0000 0110   --------- = 0010 0011

Once again, the adjustment gives us the correct answer:

0010 0011 = 23 10

• Engineering Mathematics
• Discrete Mathematics
• Operating System
• Computer Networks
• Digital Logic and Design
• C Programming
• Data Structures
• Theory of Computation
• Compiler Design
• Computer Org and Architecture
• Floating Point Representation - Basics
• Fixed Point Representation
• Introduction of Floating Point Representation
• Binary Representations in Digital Logic
• IEEE Standard 754 Floating Point Numbers
• C | Pointer Basics | Question 3
• C | Pointer Basics | Question 17
• Matlab Floating Point Precision
• Why floating-point values do not represent exact value
• Floating point error in Python
• std is_floating_point Template in C++
• How to Catch Floating Point Errors in C++?
• Display scientific notation as float in Python
• Division Algorithm in Signed Magnitude Representation
• C++ Floating Point Manipulation
• sizeof() for Floating Constant in C
• Program for conversion of 32 Bits Single Precision IEEE 754 Floating Point Representation
• How to count set bits in a floating point number in C?
• Convert a floating point number to string in C
• Floating point number precision in JavaScript

Floating Point Representation – Basics

There are posts on representation of floating point format. The objective of this article is to provide a brief introduction to floating point format. 

The following description explains terminology and primary details of IEEE 754 binary floating-point representation. The discussion confines to single and double precision formats. 

Usually, a real number in binary will be represented in the following format,   

I m I m-1 …I 2 I 1 I 0 .F 1 F 2 …F n F n-1

Where I m and F n will be either 0 or 1 of integer and fraction parts respectively. 

A finite number can also represented by four integers components, a sign (s), a base (b), a significant (m), and an exponent (e). Then the numerical value of the number is evaluated as   

(-1) s x m x b e ________ Where m < |b|

Depending on base and the number of bits used to encode various components, the IEEE 754 standard defines five basic formats. Among the five formats, the binary32 and the binary64 formats are single precision and double precision formats respectively in which the base is 2.   

Table – 1 Precision Representation

Single Precision Format:  

As mentioned in Table 1 the single precision format has 23 bits for significant (1 represents implied bit, details below), 8 bits for exponent and 1 bit for sign. 

For example, the rational number 9÷2 can be converted to single precision float format as following,   

9 (10) ÷ 2 (10) = 4.5 (10) = 100.1 (2)

The result said to be normalized , if it is represented with leading 1 bit, i.e. 1.001 (2) x 2 2 . (Similarly when the number 0.000000001101 (2) x 2 3 is normalized, it appears as 1.101 (2) x 2 -6 ). Omitting this implied 1 on left extreme gives us the mantissa of float number. A normalized number provides more accuracy than corresponding de-normalized number. The implied most significant bit can be used to represent even more accurate significant (23 + 1 = 24 bits) which is called subnormal representation. The floating point numbers are to be represented in normalized form . 

The subnormal numbers fall into the category of de-normalized numbers. The subnormal representation slightly reduces the exponent range and can’t be normalized since that would result in an exponent which doesn’t fit in the field. Subnormal numbers are less accurate, i.e. they have less room for nonzero bits in the fraction field, than normalized numbers. Indeed, the accuracy drops as the size of the subnormal number decreases. However, the subnormal representation is useful in filing gaps of floating point scale near zero. 

In other words, the above result can be written as (-1) 0 x 1.001 (2) x 2 2 which yields the integer components as s = 0, b = 2, significant (m) = 1.001, mantissa = 001 and e = 2. The corresponding single precision floating number can be represented in binary as shown below, 

Where the exponent field is supposed to be 2, yet encoded as 129 (127+2) called biased exponent . The exponent field is in plain binary format which also represents negative exponents with an encoding (like sign magnitude, 1’s complement, 2’s complement, etc.). The biased exponent is used for the representation of negative exponents. The biased exponent has advantages over other negative representations in performing bitwise comparing of two floating point numbers for equality. 

A bias of (2 n-1 – 1), where n is # of bits used in exponent, is added to the exponent (e) to get biased exponent ( E ). So, the biased exponent ( E ) of single precision number can be obtained as   

E = e + 127

The range of exponent in single precision format is -128 to +127. Other values are used for special symbols. 

Note: When we unpack a floating point number the exponent obtained is the biased exponent. Subtracting 127 from the biased exponent we can extract unbiased exponent.  

Double Precision Format:  

As mentioned in Table – 1 the double precision format has 52 bits for significant (1 represents implied bit), 11 bits for exponent and 1 bit for sign. All other definitions are same for double precision format, except for the size of various components. 

Precision:  

The smallest change that can be represented in floating point representation is called as precision. The fractional part of a single precision normalized number has exactly 23 bits of resolution, (24 bits with the implied bit). This corresponds to log (10) (2 23 ) = 6.924 = 7 (the characteristic of logarithm) decimal digits of accuracy. Similarly, in case of double precision numbers the precision is log (10) (2 52 ) = 15.654 = 16 decimal digits. 

Accuracy:  

Accuracy in floating point representation is governed by number of significant bits, whereas range is limited by exponent. Not all real numbers can exactly be represented in floating point format. For any numberwhich is not floating point number, there are two options for floating point approximation, say, the closest floating point number less than x as x_ and the closest floating point number greater than x as x+. A rounding operation is performed on number of significant bits in the mantissa field based on the selected mode. The round down mode causes x set to x_, the round up mode causes x set to x+, the round towards zero mode causes x is either x_ or x+ whichever is between zero and. The round to nearest mode sets x to x_ or x+ whichever is nearest to x. Usually round to nearest is most used mode. The closeness of floating point representation to the actual value is called as accuracy . 

Special Bit Patterns:  

The standard defines few special floating point bit patterns. Zero can’t have most significant 1 bit, hence can’t be normalized. The hidden bit representation requires a special technique for storing zero. We will have two different bit patterns +0 and -0 for the same numerical value zero. For single precision floating point representation, these patterns are given below, 

0 00000000 00000000000000000000000 = +0 

1 00000000 00000000000000000000000 = -0 

Similarly, the standard represents two different bit patterns for +INF and -INF. The same are given below, 

0 11111111 00000000000000000000000 = +INF 

1 11111111 00000000000000000000000 = -INF 

All of these special numbers, as well as other special numbers (below) are subnormal numbers, represented through the use of a special bit pattern in the exponent field. This slightly reduces the exponent range, but this is quite acceptable since the range is so large. 

An attempt to compute expressions like 0 x INF, 0 ÷ INF, etc. make no mathematical sense. The standard calls the result of such expressions as Not a Number (NaN). Any subsequent expression with NaN yields NaN. The representation of NaN has non-zero significant and all 1s in the exponent field. These are shown below for single precision format (x is don’t care bits), 

x 11111111 m 0000000000000000000000 

Where m can be 0 or 1. This gives us two different representations of NaN. 

0 11111111 0 0000000000000000000001 _____________ Signaling NaN (SNaN) 

0 11111111 1 0000000000000000000001 _____________Quiet NaN (QNaN) 

Usually QNaN and SNaN are used for error handling. QNaN do not raise any exceptions as they propagate through most operations. Whereas SNaN are which when consumed by most operations will raise an invalid exception. 

Overflow and Underflow:  

Overflow is said to occur when the true result of an arithmetic operation is finite but larger in magnitude than the largest floating point number which can be stored using the given precision. Underflow is said to occur when the true result of an arithmetic operation is smaller in magnitude (infinitesimal) than the smallest normalized floating point number which can be stored. Overflow can’t be ignored in calculations whereas underflow can effectively be replaced by zero. 

Endianness:  

The IEEE 754 standard defines a binary floating point format. The architecture details are left to the hardware manufacturers. The storage order of individual bytes in binary floating point numbers varies from architecture to architecture. 

Thanks to Venki for writing the above article.  

Please Login to comment...

Similar reads.

• Digital Logic

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Number Systems

The number system is a way to represent or express numbers.  You have heard of various types of number systems such as the whole numbers and the real numbers. But in the context of computers, we define other types of number systems. They are:

• The decimal number system
• The binary number system
• The octal number system and
• The hexadecimal number system

Suggested Videos

Decimal number system (base 10), browse more topics under basics of computers.

• Number Systems Conversions
• Generations of Computers
• Computer Organisation
• Computer Memory
• History of Computers
• Computers Abbreviations
• Basic Computer Terminology
• Computer Languages
• Basic Internet Knowledge and Protocols
• Hardware and Software
• Keyboard Shortcuts
• I/O Devices
• Practice Problems On Basics Of Computers

Binary Number System (Base 2)

Want to see how smart you are? Want to exercise your brain? Click here for a wonderfully explained and lucid section of Reasoning Ability.

Units of measurement of data

Octal Number System (Base 8)

Hexadecimal number system (base 16).

Having trouble with concepts like DBMS? Have an important exam soon? Click here and start your preparations now!

Number System Chart

Example for you.

Preparing for a job exam and can’t find the complete coverage of topics? No worries we are here to help!

Click here to learn everything you need to know about the English Language .

Find all the topics of Reasoning Ability here!

We have the most complete syllabus of quantitative aptitude in one place for you! Click here

Practice Questions

Q 1: How would you represent 10111 in the decimal number system?

Q 2: The LSB and MSB in the following number are: 1220

A) 1 & 0

B) 0 & 1

Ans: A) 0 & 1

Stay updated and don’t get stuck in an exam. Prepare your General Awareness topics here.

Customize your course in 30 seconds

Which class are you in.

Basics of Computers

• Computer Abbreviations
• Basic Computer Knowledge – Practice Problems
• Computer Organization
• Input and Output (I/O) Devices

One response to “Hardware and Software”

THANKS ,THIS IS THE VERY USEFUL KNOWLEDGE

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

Isaac Computer Science

You need to enable JavaScript to access Isaac Computer Science.

LGBTQ representation in government is growing but still disproportionate: Graphics explain

Those identifying as gay represented the largest share of lgbtq elected officials, with 544 gay men in public office within local, state and federal governments.

Nearly 1,300 elected officials in the U.S. are a part of the LGBTQ community − a number that continues to grow every election cycle but still falls far short of being representative of the LGBTQ community.

About 7.6% of U.S. adults now identify as lesbian, gay, bisexual, transgender, queer, or as something other than heterosexual, according to a recent Gallup poll . That’s compared to 3.5% in 2012, the year the national polling agency began measuring sexual orientation and transgender identity.

While 7.6% of adults identify as LGBTQ+, less than 1% of elected officials in the U.S. identify the same, though there's no way to quantify those who hold office but haven't come out publicly.

In order for the government to be fully representative of the queer population, more than 35,000 LGBTQ people would need to be elected, according to the Victory Institute , a nonprofit focused on training LGBTQ+ leaders to run for office.

Although the LGBTQ community is underrepresented in government, an annual report by the organization did identify gains in several areas.

LGBTQ+ representation in government

According to the most recent year of data available (2022), those identifying as gay represented the largest share of LGBTQ elected officials, with 544 gay men in public office within local, state and federal governments.

The following groups made gains between 2021 and 2022:

• Non-binary and genderqueer elected officials increased from nine to 12
• Transgender elected officials grew from 41 to 45
• Bisexual elected officials increased from 71 to 90 during the same time period

The growing number of adults identifying as LGBTQ+ represents a greater sense of societal acceptance and/or support systems for those who identify as queer, Brandon Robinson, an associate professor and department chair of gender and sexuality studies at the University of California, Riverside, previously told USA TODAY.

"More people identifying as LGBTQ is often a sign that more people feel safe and/or comfortable to openly claim an LGBTQ identity," they said.

Map shows which states have LGBTQ+ representation in public office

Alabama, Wyoming and Idaho all have one elected official that identifies as queer. California, Illinois, Pennsylvania, Massachusetts and Michigan all have more than 50 LGBTQ+ elected officials serving in local, state and federal office.

Ten states have fewer LGBTQ+ elected officials in 2022 compared to 2021. During the same time period, 22 states have more LGBTQ+ elected officials, the Victory Institute reported.

Between June 2021 and 2022, the share of LGBTQ+ elected officials who were affiliated with the Democratic Party increased from 73.1% to 75.1%. The share of LGBTQ elected officials that are affiliated with the Republican party was much smaller, at 3%.

"LGBTQ elected officials are on the front lines of defending our rights and freedoms, which are under threat at every level of government," Victory Institute President and CEO Annise Parker, also the mayor of Houston, says on the group's website. "LGBTQ elected officials represent the strength and diversity of not only who we are as a society now, but also the America we aspire to build for future generations."

Data trends: Portion of US adults identifying as LGBTQ has more than doubled in last 12 years

More than just 'firsts': LGBTQ elected officials carve space for a future generation of politicians

Contributing: Marc Ramirez

What Seeing The Angel Number 111 Really Means For Your Life, According To A Numerologist

Hint: It's a sign that new beginnings are on the horizon.

ICYDK, 111 is an angel number . Angel numbers are repetitive numbers or sequences within numerology said to carry messages from the universe, Women’s Health previously reported . “Each number has its own energetic vibration and symbolic meaning,” says Johanna Aúgusta , a professional numerologist. The number 1, in particular, is the first numerical vibration and a powerful symbol for new beginnings in numerology , per Aúgusta.

This energy can also represent an opportunity for growth and development. “By harnessing this power, you can create positive changes in your life and manifest your desires with ease,” says Aúgusta. “When the number 1 appears throughout your readings or in your day-to-day life, such as when looking at a clock, trust that it is urging you to step into your power and blaze your own trail.”

If you are noticing 111 everywhere you go, keep reading to find out what that angel number really means and how you can harness its specific energy to empower your life.

What does the number 1 represent in numerology?

“In numerology, the number one symbolizes new beginnings, fresh starts, and motivation,” says Aúgusta. “It’s associated with taking initiative and striving forward.” Think about it: The number one starts all orders of things so it makes perfect sense that it reveals something new is on the horizon.

If you’re going through a challenging time, or just searching for inspiration, let seeing 111 shed a bit of light in your path—change is coming. Maybe it’s the birth of a new idea, which will make you reconsider your current position or push you to take on a new project. Perhaps, it’s a sign that a business idea you’ve been working so hard on behind the scenes will finally come into fruition. Whatever is brewing, you’re definitely stepping into your lucky girl era .

What does the angel number 111 mean?

Per Aúgusta, angel number 111 is a sign of encouragement and support: “It signifies that you are on the right path.” If you’ve been wary about a decision you recently made or wondering if you’re headed in the right direction, take seeing this angel number as an encouraging wink.

As the number one brings with it motivational and renewed energy, “it’s a reminder to stay positive, focus on your desires, and be grateful for what you have in life,” says Aúgusta.

What does 111 mean for my love life?

As mentioned, the angel number 111 is a powerful symbol of new beginnings and this translates into your love life, as well, Aúgusta notes. Whatever season you’re in when it comes to romance, here’s what seeing 111 means for you:

• If you’re single: Seeing 111 is highly promising. Take this sighting as a nudge to go out and explore new territory so that you might “bump” into your new fling or potential beau. Stop by that bar that just opened across the street. Finally sign up for that pottery class you’ve been eyeing. Put yourself out there because your love life is about to get a lot more interesting.
• If you’re in a relationship: If you’re happily in l-o-v-e, then you can rest assured that you’re supported and deserve to relish in that joy. “Angel number 111 signifies that you deserve love and are on the right path to finding your soulmate,” says Aúgusta. So go on, full steam ahead.
• If you’re going through a break up: If you have a break up pending, but have been putting it off because you don’t want to deal with those feelings (it’s tough, I know), this is your sign to be honest about where you stand. “[The angel number 111] often appears when you are ready to release old patterns and relationships that no longer serve you,” says Aúgusta. In other words, it’s time to release and let go. You might find that true love is awaiting in the next chapter of your life, but you won’t reach it if you don’t turn the page first.

Speaking about relationships, angel number 111 can also reveal things about a twin flame connection , according to Aúgusta. FYI, a twin flame is basically your ultimate karmic soulmate, Women’s Health previously reported. They make you feel complete and there’s a natural magnetism between you two—almost as if they’re a mirror image of yourself.

If you see the number 111 frequently, it may signify that you are about to meet your twin flame, says Aúgusta. It can also mean that “you are already in a very compatible relationship,” she adds. TL;DR: “Pay attention to the signs and synchronicities around you, and trust that the universe is guiding you toward your greatest good,” says Aúgusta.

What does 111 mean for my finances and career?

When it comes to money matters , seeing the angel number 111 is a sign that now is the time to make a change or take action. “If you want to manifest more money or create a new business, this is a great time to take inspired action and stay focused on your goals,” says Aúgusta. That means that if you’re plotting a career change, or wanting to take a big step, this is your moment to go for it.

The number one is a sign of abundance, so whether you’re eager to begin your business venture, or looking for new opportunities to put more money in your pocket, spotting 111 asks you to take the chance to invest in yourself. Prosperity is on the horizon.

Why do I keep seeing 111 everywhere?

Seeing the number 111 everywhere is akin to getting a memo from the universe and your guardian angels that you’re a-okay. It’s reassurance “that you are on the right path and that your angels support and guide you,” says Aúgusta. Whether you’re spiritual or just plain curious about why you keep spotting the sequence 111, let it reveal to you a positive message: You’re supported on whatever route you choose to follow.

“Pay attention to your thoughts and feelings when you see this number, as it may hold a specific message or guidance for you,” Aúgusta advises. For example, if you’re feeling anxious about a big move, seeing 111 is an encouraging sign that everything will be fine—hey, you might even thrive in this new environment.

How do I harness the power of 111 energy?

Seeing the angel number 111 is the universe telling you that you gotta have faith in yourself—really though. “Trust in yourself and the universe, knowing that you are supported on your path,” Aúgusta reiterates.

If the number 111 keeps showing up in your life, “it’s essential to stay positive and focused on your desires,” Aúgusta adds. “Visualize your goals and dreams, and take inspired action toward making them a reality.” Maybe you can practice some positive psychology and put together a vision board , as placing an image to those goals you have in mind can motivate you to work towards them.

Additionally, “practice gratitude for what you have,” says Aúgusta—you might even want to try keeping a gratitude journal . You can make a list of things you are grateful for each day, and jot down the things you’d like to attract and manifest for your future.

Case in point: It’s time to embody confidence and take a step forward. You got this!

Karina Castrillo is a freelance writer, paid leave advocate, communications specialist at a New Jersey-based labor union, and a Libra. She was formerly a travel writer at Culture Trip where she reviewed restaurants and cultural events in both Paris and Miami. Outside of spending a lot of time at coffee shops in the West Village or perusing vintage shops in Greenpoint, you can find her writing her next zine or at a social justice movement rally. 

Here's Exactly How To Break Up With Your Therapist

Princess Diana’s Siblings Support Prince Harry

Your June 2024 Horoscope Is Here

Why Travis Kelce Remained in the U.S. This Weekend

Boost Your Mood With This Happy Song Playlist

All The Pregnant Celebrities With 2024 Due Dates

All About Nika Mühl's Little Sister Hana Mühl

All About 'Unrivaled,' The New WNBA 3x3 League

Angel Reese and Caitlin Clark's On-Court History

Iga Swiatek And Aryna Sabalenka's History, Rivalry

Everything To Know About Gypsy Rose Blanchard

Help | Advanced Search

Computer Science > Computer Vision and Pattern Recognition

Title: retrieval meets reasoning: even high-school textbook knowledge benefits multimodal reasoning.

Abstract: Large language models equipped with retrieval-augmented generation (RAG) represent a burgeoning field aimed at enhancing answering capabilities by leveraging external knowledge bases. Although the application of RAG with language-only models has been extensively explored, its adaptation into multimodal vision-language models remains nascent. Going beyond mere answer generation, the primary goal of multimodal RAG is to cultivate the models' ability to reason in response to relevant queries. To this end, we introduce a novel multimodal RAG framework named RMR (Retrieval Meets Reasoning). The RMR framework employs a bi-modal retrieval module to identify the most relevant question-answer pairs, which then serve as scaffolds for the multimodal reasoning process. This training-free approach not only encourages the model to engage deeply with the reasoning processes inherent in the retrieved content but also facilitates the generation of answers that are precise and richly interpretable. Surprisingly, utilizing solely the ScienceQA dataset, collected from elementary and high school science curricula, RMR significantly boosts the performance of various vision-language models across a spectrum of benchmark datasets, including A-OKVQA, MMBench, and SEED. These outcomes highlight the substantial potential of our multimodal retrieval and reasoning mechanism to improve the reasoning capabilities of vision-language models.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .