- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

One-Tailed and Two-Tailed Hypothesis Tests Explained
By Jim Frost 60 Comments
Choosing whether to perform a one-tailed or a two-tailed hypothesis test is one of the methodology decisions you might need to make for your statistical analysis. This choice can have critical implications for the types of effects it can detect, the statistical power of the test, and potential errors.
In this post, you’ll learn about the differences between one-tailed and two-tailed hypothesis tests and their advantages and disadvantages. I include examples of both types of statistical tests. In my next post, I cover the decision between one and two-tailed tests in more detail.
What Are Tails in a Hypothesis Test?
First, we need to cover some background material to understand the tails in a test. Typically, hypothesis tests take all of the sample data and convert it to a single value, which is known as a test statistic. You’re probably already familiar with some test statistics. For example, t-tests calculate t-values . F-tests, such as ANOVA, generate F-values . The chi-square test of independence and some distribution tests produce chi-square values. All of these values are test statistics. For more information, read my post about Test Statistics .
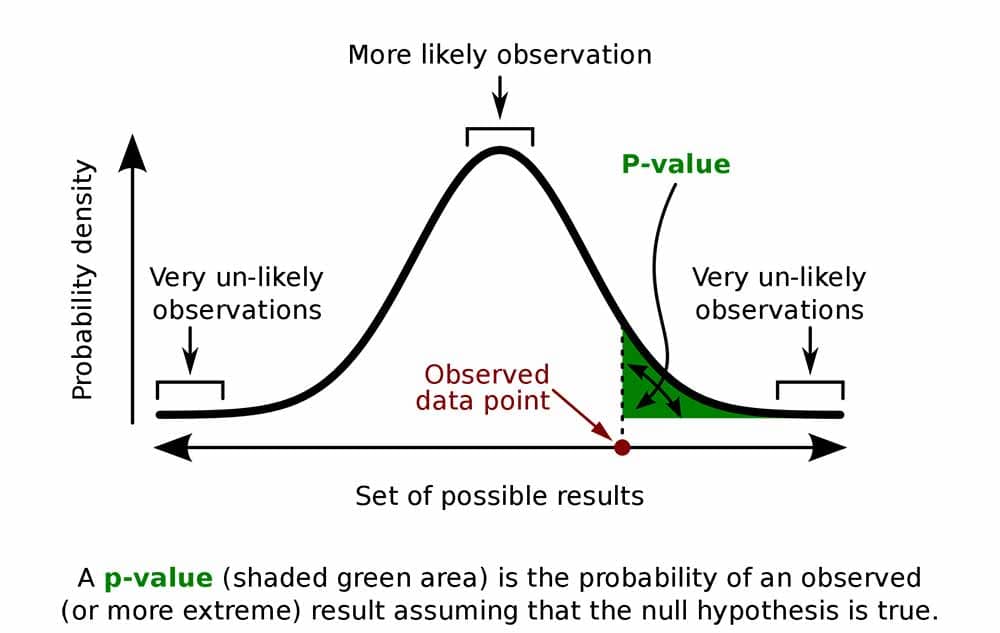
These test statistics follow a sampling distribution. Probability distribution plots display the probabilities of obtaining test statistic values when the null hypothesis is correct. On a probability distribution plot, the portion of the shaded area under the curve represents the probability that a value will fall within that range.
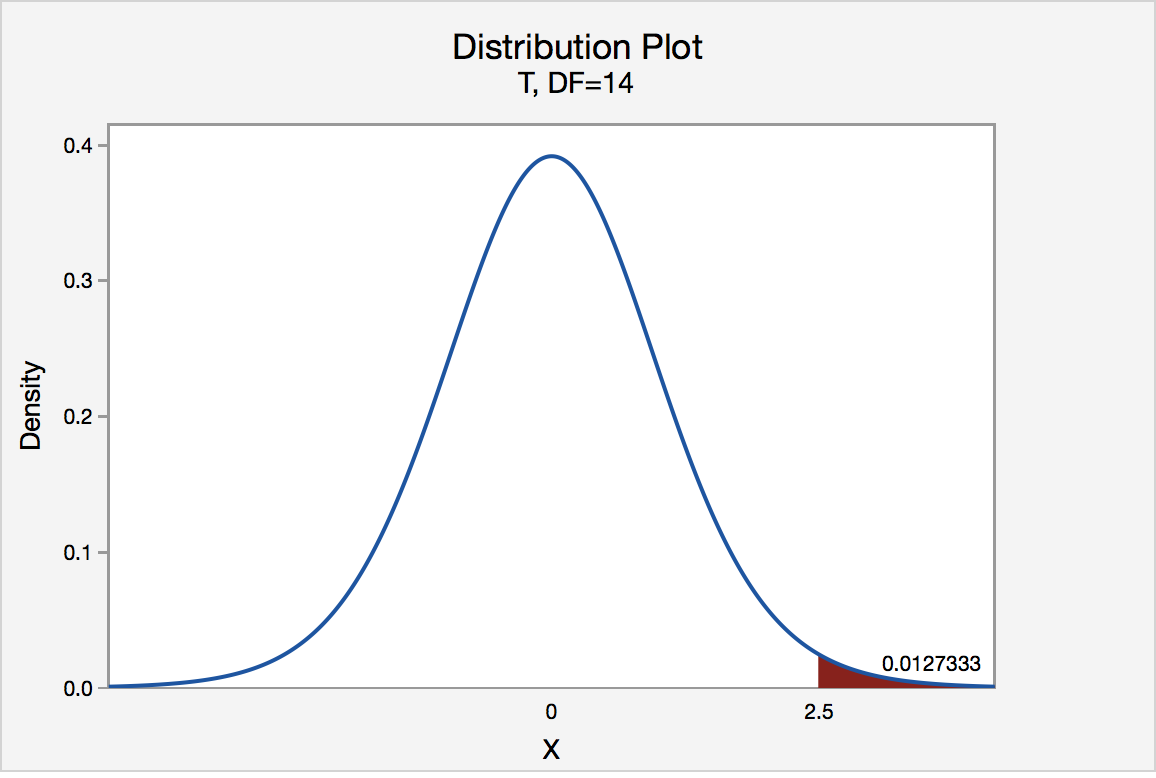
The graph below displays a sampling distribution for t-values. The two shaded regions cover the two-tails of the distribution.

Keep in mind that this t-distribution assumes that the null hypothesis is correct for the population. Consequently, the peak (most likely value) of the distribution occurs at t=0, which represents the null hypothesis in a t-test. Typically, the null hypothesis states that there is no effect. As t-values move further away from zero, it represents larger effect sizes. When the null hypothesis is true for the population, obtaining samples that exhibit a large apparent effect becomes less likely, which is why the probabilities taper off for t-values further from zero.
Related posts : How t-Tests Work and Understanding Probability Distributions
Critical Regions in a Hypothesis Test
In hypothesis tests, critical regions are ranges of the distributions where the values represent statistically significant results. Analysts define the size and location of the critical regions by specifying both the significance level (alpha) and whether the test is one-tailed or two-tailed.
Consider the following two facts:
- The significance level is the probability of rejecting a null hypothesis that is correct.
- The sampling distribution for a test statistic assumes that the null hypothesis is correct.
Consequently, to represent the critical regions on the distribution for a test statistic, you merely shade the appropriate percentage of the distribution. For the common significance level of 0.05, you shade 5% of the distribution.
Related posts : Significance Levels and P-values and T-Distribution Table of Critical Values
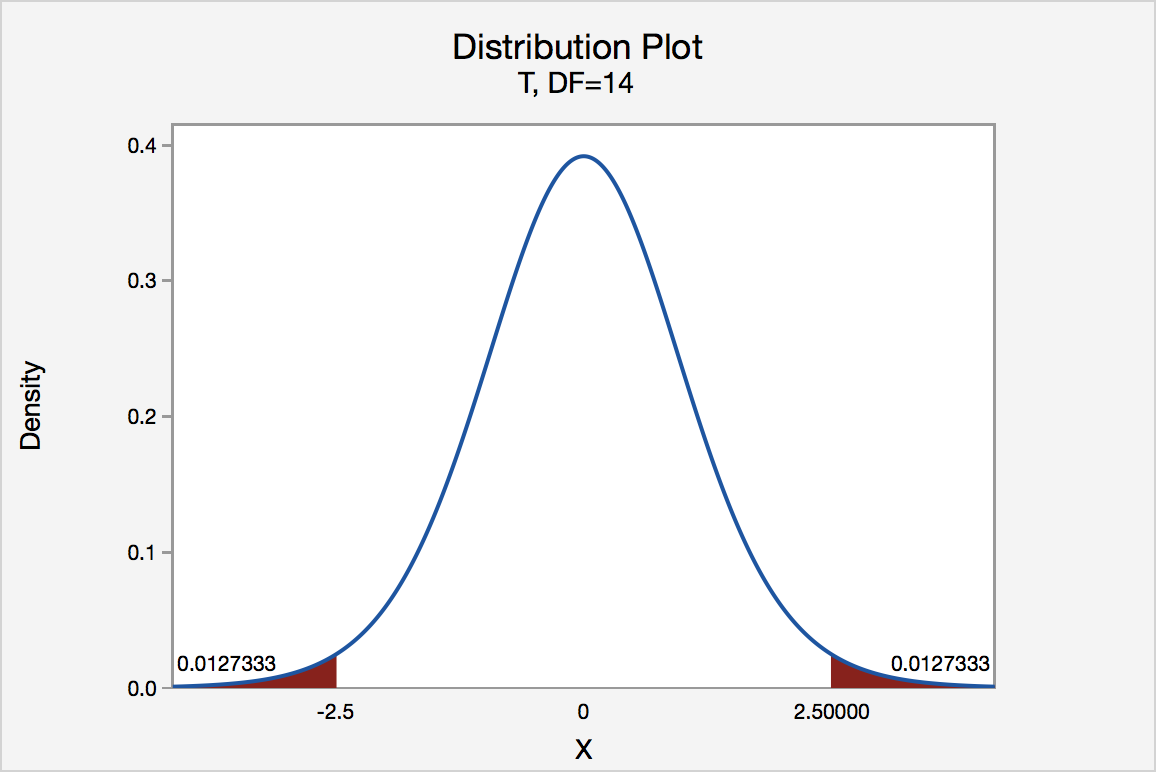
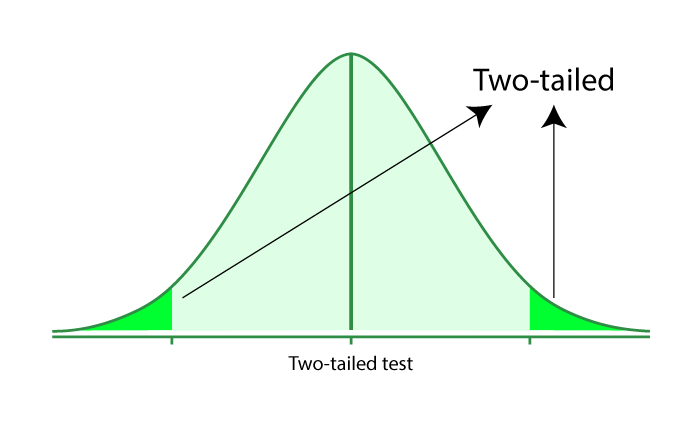
Two-Tailed Hypothesis Tests
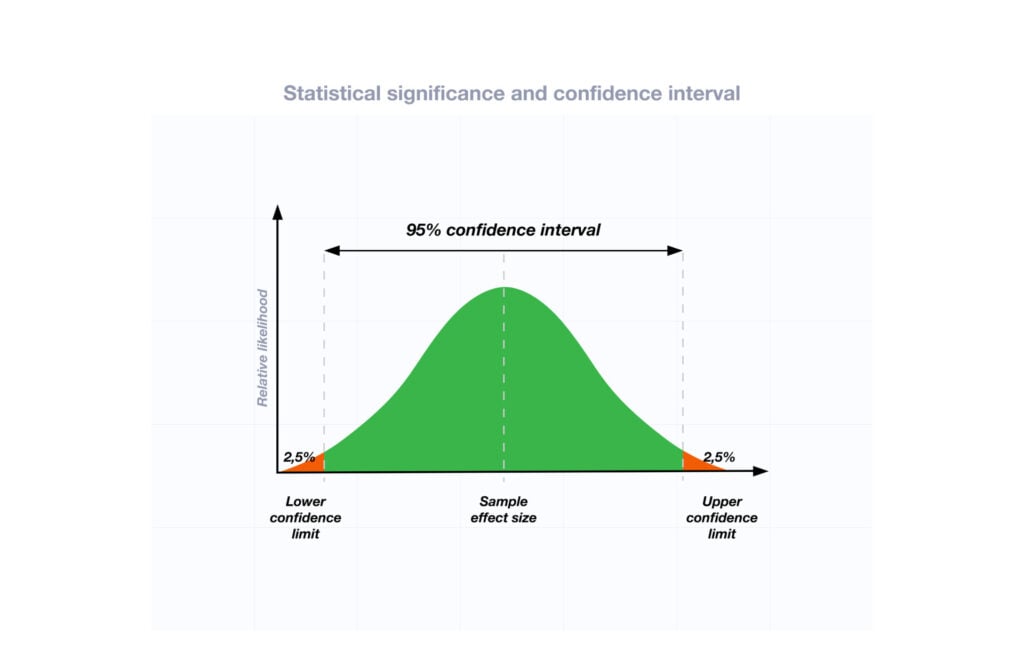
Two-tailed hypothesis tests are also known as nondirectional and two-sided tests because you can test for effects in both directions. When you perform a two-tailed test, you split the significance level percentage between both tails of the distribution. In the example below, I use an alpha of 5% and the distribution has two shaded regions of 2.5% (2 * 2.5% = 5%).
When a test statistic falls in either critical region, your sample data are sufficiently incompatible with the null hypothesis that you can reject it for the population.
In a two-tailed test, the generic null and alternative hypotheses are the following:
- Null : The effect equals zero.
- Alternative : The effect does not equal zero.
The specifics of the hypotheses depend on the type of test you perform because you might be assessing means, proportions, or rates.
Example of a two-tailed 1-sample t-test
Suppose we perform a two-sided 1-sample t-test where we compare the mean strength (4.1) of parts from a supplier to a target value (5). We use a two-tailed test because we care whether the mean is greater than or less than the target value.
To interpret the results, simply compare the p-value to your significance level. If the p-value is less than the significance level, you know that the test statistic fell into one of the critical regions, but which one? Just look at the estimated effect. In the output below, the t-value is negative, so we know that the test statistic fell in the critical region in the left tail of the distribution, indicating the mean is less than the target value. Now we know this difference is statistically significant.

We can conclude that the population mean for part strength is less than the target value. However, the test had the capacity to detect a positive difference as well. You can also assess the confidence interval. With a two-tailed hypothesis test, you’ll obtain a two-sided confidence interval. The confidence interval tells us that the population mean is likely to fall between 3.372 and 4.828. This range excludes the target value (5), which is another indicator of significance.
Advantages of two-tailed hypothesis tests
You can detect both positive and negative effects. Two-tailed tests are standard in scientific research where discovering any type of effect is usually of interest to researchers.
One-Tailed Hypothesis Tests
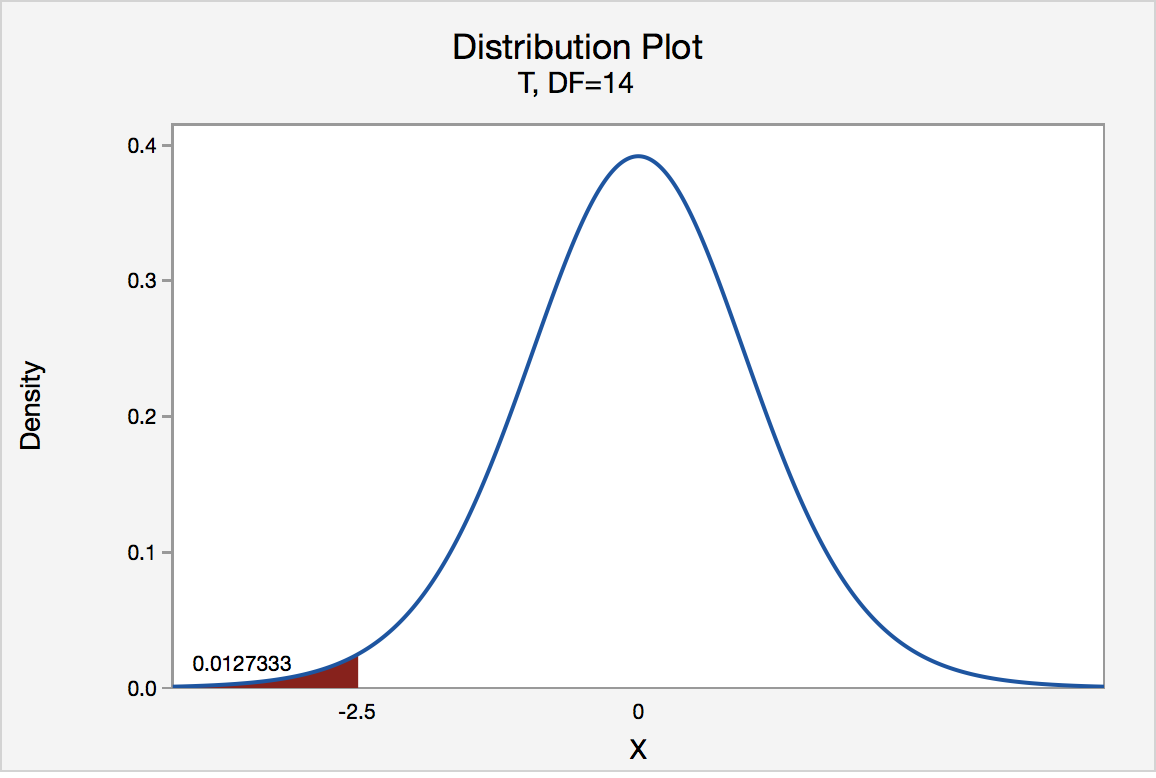
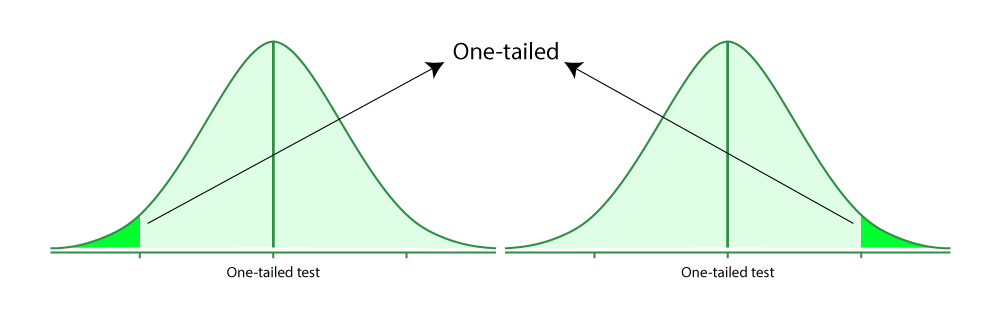
One-tailed hypothesis tests are also known as directional and one-sided tests because you can test for effects in only one direction. When you perform a one-tailed test, the entire significance level percentage goes into the extreme end of one tail of the distribution.
In the examples below, I use an alpha of 5%. Each distribution has one shaded region of 5%. When you perform a one-tailed test, you must determine whether the critical region is in the left tail or the right tail. The test can detect an effect only in the direction that has the critical region. It has absolutely no capacity to detect an effect in the other direction.
In a one-tailed test, you have two options for the null and alternative hypotheses, which corresponds to where you place the critical region.
You can choose either of the following sets of generic hypotheses:
- Null : The effect is less than or equal to zero.
- Alternative : The effect is greater than zero.

- Null : The effect is greater than or equal to zero.
- Alternative : The effect is less than zero.

Again, the specifics of the hypotheses depend on the type of test you perform.
Notice how for both possible null hypotheses the tests can’t distinguish between zero and an effect in a particular direction. For example, in the example directly above, the null combines “the effect is greater than or equal to zero” into a single category. That test can’t differentiate between zero and greater than zero.
Example of a one-tailed 1-sample t-test
Suppose we perform a one-tailed 1-sample t-test. We’ll use a similar scenario as before where we compare the mean strength of parts from a supplier (102) to a target value (100). Imagine that we are considering a new parts supplier. We will use them only if the mean strength of their parts is greater than our target value. There is no need for us to differentiate between whether their parts are equally strong or less strong than the target value—either way we’d just stick with our current supplier.
Consequently, we’ll choose the alternative hypothesis that states the mean difference is greater than zero (Population mean – Target value > 0). The null hypothesis states that the difference between the population mean and target value is less than or equal to zero.

To interpret the results, compare the p-value to your significance level. If the p-value is less than the significance level, you know that the test statistic fell into the critical region. For this study, the statistically significant result supports the notion that the population mean is greater than the target value of 100.
Confidence intervals for a one-tailed test are similarly one-sided. You’ll obtain either an upper bound or a lower bound. In this case, we get a lower bound, which indicates that the population mean is likely to be greater than or equal to 100.631. There is no upper limit to this range.
A lower-bound matches our goal of determining whether the new parts are stronger than our target value. The fact that the lower bound (100.631) is higher than the target value (100) indicates that these results are statistically significant.
This test is unable to detect a negative difference even when the sample mean represents a very negative effect.
Advantages and disadvantages of one-tailed hypothesis tests
One-tailed tests have more statistical power to detect an effect in one direction than a two-tailed test with the same design and significance level. One-tailed tests occur most frequently for studies where one of the following is true:
- Effects can exist in only one direction.
- Effects can exist in both directions but the researchers only care about an effect in one direction. There is no drawback to failing to detect an effect in the other direction. (Not recommended.)
The disadvantage of one-tailed tests is that they have no statistical power to detect an effect in the other direction.
As part of your pre-study planning process, determine whether you’ll use the one- or two-tailed version of a hypothesis test. To learn more about this planning process, read 5 Steps for Conducting Scientific Studies with Statistical Analyses .
This post explains the differences between one-tailed and two-tailed statistical hypothesis tests. How these forms of hypothesis tests function is clear and based on mathematics. However, there is some debate about when you can use one-tailed tests. My next post explores this decision in much more depth and explains the different schools of thought and my opinion on the matter— When Can I Use One-Tailed Hypothesis Tests .
If you’re learning about hypothesis testing and like the approach I use in my blog, check out my Hypothesis Testing book! You can find it at Amazon and other retailers.

Share this:

Reader Interactions
June 26, 2022 at 12:14 pm
Hi, Can help me with figuring out the null and alternative hypothesis of the following statement? Some claimed that the real average expenditure on beverage by general people is at least $10.
February 19, 2022 at 6:02 am
thank you for the thoroughly explanation, I’m still strugling to wrap my mind around the t-table and the relation between the alpha values for one or two tail probability and the confidence levels on the bottom (I’m understanding it so wrongly that for me it should be the oposite, like one tail 0,05 should correspond 95% CI and two tailed 0,025 should correspond to 95% because then you got the 2,5% on each side). In my mind if I picture the one tail diagram with an alpha of 0,05 I see the rest 95% inside the diagram, but for a one tail I only see 90% CI paired with a 5% alpha… where did the other 5% go? I tried to understand when you said we should just double the alpha for a one tail probability in order to find the CI but I still cant picture it. I have been trying to understand this. Like if you only have one tail and there is 0,05, shouldn’t the rest be on the other side? why is it then 90%… I know I’m missing a point and I can’t figure it out and it’s so frustrating…
February 23, 2022 at 10:01 pm
The alpha is the total shaded area. So, if the alpha = 0.05, you know that 5% of the distribution is shaded. The number of tails tells you how to divide the shaded areas. Is it all in one region (1-tailed) or do you split the shaded regions in two (2-tailed)?
So, for a one-tailed test with an alpha of 0.05, the 5% shading is all in one tail. If alpha = 0.10, then it’s 10% on one side. If it’s two-tailed, then you need to split that 10% into two–5% in both tails. Hence, the 5% in a one-tailed test is the same as a two-tailed test with an alpha of 0.10 because that test has the same 5% on one side (but there’s another 5% in the other tail).
It’s similar for CIs. However, for CIs, you shade the middle rather than the extremities. I write about that in one my articles about hypothesis testing and confidence intervals .
I’m not sure if I’m answering your question or not.
February 17, 2022 at 1:46 pm
I ran a post hoc Dunnett’s test alpha=0.05 after a significant Anova test in Proc Mixed using SAS. I want to determine if the means for treatment (t1, t2, t3) is significantly less than the means for control (p=pathogen). The code for the dunnett’s test is – LSmeans trt / diff=controll (‘P’) adjust=dunnett CL plot=control; I think the lower bound one tailed test is the correct test to run but I’m not 100% sure. I’m finding conflicting information online. In the output table for the dunnett’s test the mean difference between the control and the treatments is t1=9.8, t2=64.2, and t3=56.5. The control mean estimate is 90.5. The adjusted p-value by treatment is t1(p=0.5734), t2 (p=.0154) and t3(p=.0245). The adjusted lower bound confidence limit in order from t1-t3 is -38.8, 13.4, and 7.9. The adjusted upper bound for all test is infinity. The graphical output for the dunnett’s test in SAS is difficult to understand for those of us who are beginner SAS users. All treatments appear as a vertical line below the the horizontal line for control at 90.5 with t2 and t3 in the shaded area. For treatment 1 the shaded area is above the line for control. Looking at just the output table I would say that t2 and t3 are significantly lower than the control. I guess I would like to know if my interpretation of the outputs is correct that treatments 2 and 3 are statistically significantly lower than the control? Should I have used an upper bound one tailed test instead?
November 10, 2021 at 1:00 am
Thanks Jim. Please help me understand how a two tailed testing can be used to minimize errors in research
July 1, 2021 at 9:19 am
Hi Jim, Thanks for posting such a thorough and well-written explanation. It was extremely useful to clear up some doubts.
May 7, 2021 at 4:27 pm
Hi Jim, I followed your instructions for the Excel add-in. Thank you. I am very new to statistics and sort of enjoy it as I enter week number two in my class. I am to select if three scenarios call for a one or two-tailed test is required and why. The problem is stated:
30% of mole biopsies are unnecessary. Last month at his clinic, 210 out of 634 had benign biopsy results. Is there enough evidence to reject the dermatologist’s claim?
Part two, the wording changes to “more than of 30% of biopsies,” and part three, the wording changes to “less than 30% of biopsies…”
I am not asking for the problem to be solved for me, but I cannot seem to find direction needed. I know the elements i am dealing with are =30%, greater than 30%, and less than 30%. 210 and 634. I just don’t know what to with the information. I can’t seem to find an example of a similar problem to work with.
May 9, 2021 at 9:22 pm
As I detail in this post, a two-tailed test tells you whether an effect exists in either direction. Or, is it different from the null value in either direction. For the first example, the wording suggests you’d need a two-tailed test to determine whether the population proportion is ≠ 30%. Whenever you just need to know ≠, it suggests a two-tailed test because you’re covering both directions.
For part two, because it’s in one direction (greater than), you need a one-tailed test. Same for part three but it’s less than. Look in this blog post to see how you’d construct the null and alternative hypotheses for these cases. Note that you’re working with a proportion rather than the mean, but the principles are the same! Just plug your scenario and the concept of proportion into the wording I use for the hypotheses.
I hope that helps!
April 11, 2021 at 9:30 am
Hello Jim, great website! I am using a statistics program (SPSS) that does NOT compute one-tailed t-tests. I am trying to compare two independent groups and have justifiable reasons why I only care about one direction. Can I do the following? Use SPSS for two-tailed tests to calculate the t & p values. Then report the p-value as p/2 when it is in the predicted direction (e.g , SPSS says p = .04, so I report p = .02), and report the p-value as 1 – (p/2) when it is in the opposite direction (e.g., SPSS says p = .04, so I report p = .98)? If that is incorrect, what do you suggest (hopefully besides changing statistics programs)? Also, if I want to report confidence intervals, I realize that I would only have an upper or lower bound, but can I use the CI’s from SPSS to compute that? Thank you very much!
April 11, 2021 at 5:42 pm
Yes, for p-values, that’s absolutely correct for both cases.
For confidence intervals, if you take one endpoint of a two-side CI, it becomes a one-side bound with half the confidence level.
Consequently, to obtain a one-sided bound with your desired confidence level, you need to take your desired significance level (e.g., 0.05) and double it. Then subtract it from 1. So, if you’re using a significance level of 0.05, double that to 0.10 and then subtract from 1 (1 – 0.10 = 0.90). 90% is the confidence level you want to use for a two-sided test. After obtaining the two-sided CI, use one of the endpoints depending on the direction of your hypothesis (i.e., upper or lower bound). That’s produces the one-sided the bound with the confidence level that you want. For our example, we calculated a 95% one-sided bound.
March 3, 2021 at 8:27 am
Hi Jim. I used the one-tailed(right) statistical test to determine an anomaly in the below problem statement: On a daily basis, I calculate the (mapped_%) in a common field between two tables.
The way I used the t-test is: On any particular day, I calculate the sample_mean, S.D and sample_count (n=30) for the last 30 days including the current day. My null hypothesis, H0 (pop. mean)=95 and H1>95 (alternate hypothesis). So, I calculate the t-stat based on the sample_mean, pop.mean, sample S.D and n. I then choose the t-crit value for 0.05 from my t-ditribution table for dof(n-1). On the current day if my abs.(t-stat)>t-crit, then I reject the null hypothesis and I say the mapped_pct on that day has passed the t-test.
I get some weird results here, where if my mapped_pct is as low as 6%-8% in all the past 30 days, the t-test still gets a “pass” result. Could you help on this? If my hypothesis needs to be changed.
I would basically look for the mapped_pct >95, if it worked on a static trigger. How can I use the t-test effectively in this problem statement?
December 18, 2020 at 8:23 pm
Hello Dr. Jim, I am wondering if there is evidence in one of your books or other source you could provide, which supports that it is OK not to divide alpha level by 2 in one-tailed hypotheses. I need the source for supporting evidence in a Portfolio exercise and couldn’t find one.
I am grateful for your reply and for your statistics knowledge sharing!
November 27, 2020 at 10:31 pm
If I did a one directional F test ANOVA(one tail ) and wanted to calculate a confidence interval for each individual groups (3) mean . Would I use a one tailed or two tailed t , within my confidence interval .
November 29, 2020 at 2:36 am
Hi Bashiru,
F-tests for ANOVA will always be one-tailed for the reasons I discuss in this post. To learn more about, read my post about F-tests in ANOVA .
For the differences between my groups, I would not use t-tests because the family-wise error rate quickly grows out of hand. To learn more about how to compare group means while controlling the familywise error rate, read my post about using post hoc tests with ANOVA . Typically, these are two-side intervals but you’d be able to use one-sided.
November 26, 2020 at 10:51 am
Hi Jim, I had a question about the formulation of the hypotheses. When you want to test if a beta = 1 or a beta = 0. What will be the null hypotheses? I’m having trouble with finding out. Because in most cases beta = 0 is the null hypotheses but in this case you want to test if beta = 0. so i’m having my doubts can it in this case be the alternative hypotheses or is it still the null hypotheses?
Kind regards, Noa
November 27, 2020 at 1:21 am
Typically, the null hypothesis represents no effect or no relationship. As an analyst, you’re hoping that your data have enough evidence to reject the null and favor the alternative.
Assuming you’re referring to beta as in regression coefficients, zero represents no relationship. Consequently, beta = 0 is the null hypothesis.
You might hope that beta = 1, but you don’t usually include that in your alternative hypotheses. The alternative hypothesis usually states that it does not equal no effect. In other words, there is an effect but it doesn’t state what it is.
There are some exceptions to the above but I’m writing about the standard case.
November 22, 2020 at 8:46 am
Your articles are a help to intro to econometrics students. Keep up the good work! More power to you!
November 6, 2020 at 11:25 pm
Hello Jim. Can you help me with these please?
Write the null and alternative hypothesis using a 1-tailed and 2-tailed test for each problem. (In paragraph and symbols)
A teacher wants to know if there is a significant difference in the performance in MAT C313 between her morning and afternoon classes.
It is known that in our university canteen, the average waiting time for a customer to receive and pay for his/her order is 20 minutes. Additional personnel has been added and now the management wants to know if the average waiting time had been reduced.
November 8, 2020 at 12:29 am
I cover how to write the hypotheses for the different types of tests in this post. So, you just need to figure which type of test you need to use. In your case, you want to determine whether the mean waiting time is less than the target value of 20 minutes. That’s a 1-sample t-test because you’re comparing a mean to a target value (20 minutes). You specifically want to determine whether the mean is less than the target value. So, that’s a one-tailed test. And, you’re looking for a mean that is “less than” the target.
So, go to the one-tailed section in the post and look for the hypotheses for the effect being less than. That’s the one with the critical region on the left side of the curve.
Now, you need include your own information. In your case, you’re comparing the sample estimate to a population mean of 20. The 20 minutes is your null hypothesis value. Use the symbol mu μ to represent the population mean.
You put all that together and you get the following:
Null: μ ≥ 20 Alternative: μ 0 to denote the null hypothesis and H 1 or H A to denote the alternative hypothesis if that’s what you been using in class.
October 17, 2020 at 12:11 pm
I was just wondering if you could please help with clarifying what the hypothesises would be for say income for gamblers and, age of gamblers. I am struggling to find which means would be compared.
October 17, 2020 at 7:05 pm
Those are both continuous variables, so you’d use either correlation or regression for them. For both of those analyses, the hypotheses are the following:
Null : The correlation or regression coefficient equals zero (i.e., there is no relationship between the variables) Alternative : The coefficient does not equal zero (i.e., there is a relationship between the variables.)
When the p-value is less than your significance level, you reject the null and conclude that a relationship exists.
October 17, 2020 at 3:05 am
I was ask to choose and justify the reason between a one tailed and two tailed test for dummy variables, how do I do that and what does it mean?
October 17, 2020 at 7:11 pm
I don’t have enough information to answer your question. A dummy variable is also known as an indicator variable, which is a binary variable that indicates the presence or absence of a condition or characteristic. If you’re using this variable in a hypothesis test, I’d presume that you’re using a proportions test, which is based on the binomial distribution for binary data.
Choosing between a one-tailed or two-tailed test depends on subject area issues and, possibly, your research objectives. Typically, use a two-tailed test unless you have a very good reason to use a one-tailed test. To understand when you might use a one-tailed test, read my post about when to use a one-tailed hypothesis test .
October 16, 2020 at 2:07 pm
In your one-tailed example, Minitab describes the hypotheses as “Test of mu = 100 vs > 100”. Any idea why Minitab says the null is “=” rather than “= or less than”? No ASCII character for it?
October 16, 2020 at 4:20 pm
I’m not entirely sure even though I used to work there! I know we had some discussions about how to represent that hypothesis but I don’t recall the exact reasoning. I suspect that it has to do with the conclusions that you can draw. Let’s focus on the failing to reject the null hypothesis. If the test statistic falls in that region (i.e., it is not significant), you fail to reject the null. In this case, all you know is that you have insufficient evidence to say it is different than 100. I’m pretty sure that’s why they use the equal sign because it might as well be one.
Mathematically, I think using ≤ is more accurate, which you can really see when you look at the distribution plots. That’s why I phrase the hypotheses using ≤ or ≥ as needed. However, in terms of the interpretation, the “less than” portion doesn’t really add anything of importance. You can conclude that its equal to 100 or greater than 100, but not less than 100.
October 15, 2020 at 5:46 am
Thank you so much for your timely feedback. It helps a lot
October 14, 2020 at 10:47 am
How can i use one tailed test at 5% alpha on this problem?
A manufacturer of cellular phone batteries claims that when fully charged, the mean life of his product lasts for 26 hours with a standard deviation of 5 hours. Mr X, a regular distributor, randomly picked and tested 35 of the batteries. His test showed that the average life of his sample is 25.5 hours. Is there a significant difference between the average life of all the manufacturer’s batteries and the average battery life of his sample?
October 14, 2020 at 8:22 pm
I don’t think you’d want to use a one-tailed test. The goal is to determine whether the sample is significantly different than the manufacturer’s population average. You’re not saying significantly greater than or less than, which would be a one-tailed test. As phrased, you want a two-tailed test because it can detect a difference in either direct.
It sounds like you need to use a 1-sample t-test to test the mean. During this test, enter 26 as the test mean. The procedure will tell you if the sample mean of 25.5 hours is a significantly different from that test mean. Similarly, you’d need a one variance test to determine whether the sample standard deviation is significantly different from the test value of 5 hours.
For both of these tests, compare the p-value to your alpha of 0.05. If the p-value is less than this value, your results are statistically significant.
September 22, 2020 at 4:16 am
Hi Jim, I didn’t get an idea that when to use two tail test and one tail test. Will you please explain?
September 22, 2020 at 10:05 pm
I have a complete article dedicated to that: When Can I Use One-Tailed Tests .
Basically, start with the assumption that you’ll use a two-tailed test but then consider scenarios where a one-tailed test can be appropriate. I talk about all of that in the article.
If you have questions after reading that, please don’t hesitate to ask!
July 31, 2020 at 12:33 pm
Thank you so so much for this webpage.
I have two scenarios that I need some clarification. I will really appreciate it if you can take a look:
So I have several of materials that I know when they are tested after production. My hypothesis is that the earlier they are tested after production, the higher the mean value I should expect. At the same time, the later they are tested after production, the lower the mean value. Since this is more like a “greater or lesser” situation, I should use one tail. Is that the correct approach?
On the other hand, I have several mix of materials that I don’t know when they are tested after production. I only know the mean values of the test. And I only want to know whether one mean value is truly higher or lower than the other, I guess I want to know if they are only significantly different. Should I use two tail for this? If they are not significantly different, I can judge based on the mean values of test alone. And if they are significantly different, then I will need to do other type of analysis. Also, when I get my P-value for two tail, should I compare it to 0.025 or 0.05 if my confidence level is 0.05?
Thank you so much again.
July 31, 2020 at 11:19 pm
For your first, if you absolutely know that the mean must be lower the later the material is tested, that it cannot be higher, that would be a situation where you can use a one-tailed test. However, if that’s not a certainty, you’re just guessing, use a two-tail test. If you’re measuring different items at the different times, use the independent 2-sample t-test. However, if you’re measuring the same items at two time points, use the paired t-test. If it’s appropriate, using the paired t-test will give you more statistical power because it accounts for the variability between items. For more information, see my post about when it’s ok to use a one-tailed test .
For the mix of materials, use a two-tailed test because the effect truly can go either direction.
Always compare the p-value to your full significance level regardless of whether it’s a one or two-tailed test. Don’t divide the significance level in half.
June 17, 2020 at 2:56 pm
Is it possible that we reach to opposite conclusions if we use a critical value method and p value method Secondly if we perform one tail test and use p vale method to conclude our Ho, then do we need to convert sig value of 2 tail into sig value of one tail. That can be done just by dividing it with 2
June 18, 2020 at 5:17 pm
The p-value method and critical value method will always agree as long as you’re not changing anything about how the methodology.
If you’re using statistical software, you don’t need to make any adjustments. The software will do that for you.
However, if you calculating it by hand, you’ll need to take your significance level and then look in the table for your test statistic for a one-tailed test. For example, you’ll want to look up 5% for a one-tailed test rather than a two-tailed test. That’s not as simple as dividing by two. In this article, I show examples of one-tailed and two-tailed tests for the same degrees of freedom. The t critical value for the two-tailed test is +/- 2.086 while for the one-sided test it is 1.725. It is true that probability associated with those critical values doubles for the one-tailed test (2.5% -> 5%), but the critical value itself is not half (2.086 -> 1.725). Study the first several graphs in this article to see why that is true.
For the p-value, you can take a two-tailed p-value and divide by 2 to determine the one-sided p-value. However, if you’re using statistical software, it does that for you.
June 11, 2020 at 3:46 pm
Hello Jim, if you have the time I’d be grateful if you could shed some clarity on this scenario:
“A researcher believes that aromatherapy can relieve stress but wants to determine whether it can also enhance focus. To test this, the researcher selected a random sample of students to take an exam in which the average score in the general population is 77. Prior to the exam, these students studied individually in a small library room where a lavender scent was present. If students in this group scored significantly above the average score in general population [is this one-tailed or two-tailed hypothesis?], then this was taken as evidence that the lavender scent enhanced focus.”
Thank you for your time if you do decide to respond.
June 11, 2020 at 4:00 pm
It’s unclear from the information provided whether the researchers used a one-tailed or two-tailed test. It could be either. A two-tailed test can detect effects in both directions, so it could definitely detect an average group score above the population score. However, you could also detect that effect using a one-tailed test if it was set up correctly. So, there’s not enough information in what you provided to know for sure. It could be either.
However, that’s irrelevant to answering the question. The tricky part, as I see it, is that you’re not entirely sure about why the scores are higher. Are they higher because the lavender scent increased concentration or are they higher because the subjects have lower stress from the lavender? Or, maybe it’s not even related to the scent but some other characteristic of the room or testing conditions in which they took the test. You just know the scores are higher but not necessarily why they’re higher.
I’d say that, no, it’s not necessarily evidence that the lavender scent enhanced focus. There are competing explanations for why the scores are higher. Also, it would be best do this as an experiment with a control and treatment group where subjects are randomly assigned to either group. That process helps establish causality rather than just correlation and helps rules out competing explanations for why the scores are higher.
By the way, I spend a lot of time on these issues in my Introduction to Statistics ebook .
June 9, 2020 at 1:47 pm
If a left tail test has an alpha value of 0.05 how will you find the value in the table
April 19, 2020 at 10:35 am
Hi Jim, My question is in regards to the results in the table in your example of the one-sample T (Two-Tailed) test. above. What about the P-value? The P-value listed is .018. I assuming that is compared to and alpha of 0.025, correct?
In regression analysis, when I get a test statistic for the predictive variable of -2.099 and a p-value of 0.039. Am I comparing the p-value to an alpha of 0.025 or 0.05? Now if I run a Bootstrap for coefficients analysis, the results say the sig (2-tail) is 0.098. What are the critical values and alpha in this case? I’m trying to reconcile what I am seeing in both tables.
Thanks for your help.
April 20, 2020 at 3:24 am
Hi Marvalisa,
For one-tailed tests, you don’t need to divide alpha in half. If you can tell your software to perform a one-tailed test, it’ll do all the calculations necessary so you don’t need to adjust anything. So, if you’re using an alpha of 0.05 for a one-tailed test and your p-value is 0.04, it is significant. The procedures adjust the p-values automatically and it all works out. So, whether you’re using a one-tailed or two-tailed test, you always compare the p-value to the alpha with no need to adjust anything. The procedure does that for you!
The exception would be if for some reason your software doesn’t allow you to specify that you want to use a one-tailed test instead of a two-tailed test. Then, you divide the p-value from a two-tailed test in half to get the p-value for a one tailed test. You’d still compare it to your original alpha.
For regression, the same thing applies. If you want to use a one-tailed test for a cofficient, just divide the p-value in half if you can’t tell the software that you want a one-tailed test. The default is two-tailed. If your software has the option for one-tailed tests for any procedure, including regression, it’ll adjust the p-value for you. So, in the normal course of things, you won’t need to adjust anything.
March 26, 2020 at 12:00 pm
Hey Jim, for a one-tailed hypothesis test with a .05 confidence level, should I use a 95% confidence interval or a 90% confidence interval? Thanks
March 26, 2020 at 5:05 pm
You should use a one-sided 95% confidence interval. One-sided CIs have either an upper OR lower bound but remains unbounded on the other side.
March 16, 2020 at 4:30 pm
This is not applicable to the subject but… When performing tests of equivalence, we look at the confidence interval of the difference between two groups, and we perform two one-sided t-tests for equivalence..
March 15, 2020 at 7:51 am
Thanks for this illustrative blogpost. I had a question on one of your points though.
By definition of H1 and H0, a two-sided alternate hypothesis is that there is a difference in means between the test and control. Not that anything is ‘better’ or ‘worse’.
Just because we observed a negative result in your example, does not mean we can conclude it’s necessarily worse, but instead just ‘different’.
Therefore while it enables us to spot the fact that there may be differences between test and control, we cannot make claims about directional effects. So I struggle to see why they actually need to be used instead of one-sided tests.
What’s your take on this?
March 16, 2020 at 3:02 am
Hi Dominic,
If you’ll notice, I carefully avoid stating better or worse because in a general sense you’re right. However, given the context of a specific experiment, you can conclude whether a negative value is better or worse. As always in statistics, you have to use your subject-area knowledge to help interpret the results. In some cases, a negative value is a bad result. In other cases, it’s not. Use your subject-area knowledge!
I’m not sure why you think that you can’t make claims about directional effects? Of course you can!
As for why you shouldn’t use one-tailed tests for most cases, read my post When Can I Use One-Tailed Tests . That should answer your questions.
May 10, 2019 at 12:36 pm
Your website is absolutely amazing Jim, you seem like the nicest guy for doing this and I like how there’s no ulterior motive, (I wasn’t automatically signed up for emails or anything when leaving this comment). I study economics and found econometrics really difficult at first, but your website explains it so clearly its been a big asset to my studies, keep up the good work!
May 10, 2019 at 2:12 pm
Thank you so much, Jack. Your kind words mean a lot!
April 26, 2019 at 5:05 am
Hy Jim I really need your help now pls
One-tailed and two- tailed hypothesis, is it the same or twice, half or unrelated pls
April 26, 2019 at 11:41 am
Hi Anthony,
I describe how the hypotheses are different in this post. You’ll find your answers.
February 8, 2019 at 8:00 am
Thank you for your blog Jim, I have a Statistics exam soon and your articles let me understand a lot!
February 8, 2019 at 10:52 am
You’re very welcome! I’m happy to hear that it’s been helpful. Best of luck on your exam!
January 12, 2019 at 7:06 am
Hi Jim, When you say target value is 5. Do you mean to say the population mean is 5 and we are trying to validate it with the help of sample mean 4.1 using Hypo tests ?.. If it is so.. How can we measure a population parameter as 5 when it is almost impossible o measure a population parameter. Please clarify
January 12, 2019 at 6:57 pm
When you set a target for a one-sample test, it’s based on a value that is important to you. It’s not a population parameter or anything like that. The example in this post uses a case where we need parts that are stronger on average than a value of 5. We derive the value of 5 by using our subject area knowledge about what is required for a situation. Given our product knowledge for the hypothetical example, we know it should be 5 or higher. So, we use that in the hypothesis test and determine whether the population mean is greater than that target value.
When you perform a one-sample test, a target value is optional. If you don’t supply a target value, you simply obtain a confidence interval for the range of values that the parameter is likely to fall within. But, sometimes there is meaningful number that you want to test for specifically.
I hope that clarifies the rational behind the target value!
November 15, 2018 at 8:08 am
I understand that in Psychology a one tailed hypothesis is preferred. Is that so
November 15, 2018 at 11:30 am
No, there’s no overall preference for one-tailed hypothesis tests in statistics. That would be a study-by-study decision based on the types of possible effects. For more information about this decision, read my post: When Can I Use One-Tailed Tests?
November 6, 2018 at 1:14 am
I’m grateful to you for the explanations on One tail and Two tail hypothesis test. This opens my knowledge horizon beyond what an average statistics textbook can offer. Please include more examples in future posts. Thanks
November 5, 2018 at 10:20 am
Thank you. I will search it as well.
Stan Alekman
November 4, 2018 at 8:48 pm
Jim, what is the difference between the central and non-central t-distributions w/respect to hypothesis testing?
November 5, 2018 at 10:12 am
Hi Stan, this is something I will need to look into. I know central t-distribution is the common Student t-distribution, but I don’t have experience using non-central t-distributions. There might well be a blog post in that–after I learn more!
November 4, 2018 at 7:42 pm
this is awesome.
Comments and Questions Cancel reply
- Skip to primary navigation
- Skip to main content
- Skip to primary sidebar
Institute for Digital Research and Education
FAQ: What are the differences between one-tailed and two-tailed tests?
When you conduct a test of statistical significance, whether it is from a correlation, an ANOVA, a regression or some other kind of test, you are given a p-value somewhere in the output. If your test statistic is symmetrically distributed, you can select one of three alternative hypotheses. Two of these correspond to one-tailed tests and one corresponds to a two-tailed test. However, the p-value presented is (almost always) for a two-tailed test. But how do you choose which test? Is the p-value appropriate for your test? And, if it is not, how can you calculate the correct p-value for your test given the p-value in your output?
What is a two-tailed test?
First let’s start with the meaning of a two-tailed test. If you are using a significance level of 0.05, a two-tailed test allots half of your alpha to testing the statistical significance in one direction and half of your alpha to testing statistical significance in the other direction. This means that .025 is in each tail of the distribution of your test statistic. When using a two-tailed test, regardless of the direction of the relationship you hypothesize, you are testing for the possibility of the relationship in both directions. For example, we may wish to compare the mean of a sample to a given value x using a t-test. Our null hypothesis is that the mean is equal to x . A two-tailed test will test both if the mean is significantly greater than x and if the mean significantly less than x . The mean is considered significantly different from x if the test statistic is in the top 2.5% or bottom 2.5% of its probability distribution, resulting in a p-value less than 0.05.
What is a one-tailed test?
Next, let’s discuss the meaning of a one-tailed test. If you are using a significance level of .05, a one-tailed test allots all of your alpha to testing the statistical significance in the one direction of interest. This means that .05 is in one tail of the distribution of your test statistic. When using a one-tailed test, you are testing for the possibility of the relationship in one direction and completely disregarding the possibility of a relationship in the other direction. Let’s return to our example comparing the mean of a sample to a given value x using a t-test. Our null hypothesis is that the mean is equal to x . A one-tailed test will test either if the mean is significantly greater than x or if the mean is significantly less than x , but not both. Then, depending on the chosen tail, the mean is significantly greater than or less than x if the test statistic is in the top 5% of its probability distribution or bottom 5% of its probability distribution, resulting in a p-value less than 0.05. The one-tailed test provides more power to detect an effect in one direction by not testing the effect in the other direction. A discussion of when this is an appropriate option follows.
When is a one-tailed test appropriate?
Because the one-tailed test provides more power to detect an effect, you may be tempted to use a one-tailed test whenever you have a hypothesis about the direction of an effect. Before doing so, consider the consequences of missing an effect in the other direction. Imagine you have developed a new drug that you believe is an improvement over an existing drug. You wish to maximize your ability to detect the improvement, so you opt for a one-tailed test. In doing so, you fail to test for the possibility that the new drug is less effective than the existing drug. The consequences in this example are extreme, but they illustrate a danger of inappropriate use of a one-tailed test.
So when is a one-tailed test appropriate? If you consider the consequences of missing an effect in the untested direction and conclude that they are negligible and in no way irresponsible or unethical, then you can proceed with a one-tailed test. For example, imagine again that you have developed a new drug. It is cheaper than the existing drug and, you believe, no less effective. In testing this drug, you are only interested in testing if it less effective than the existing drug. You do not care if it is significantly more effective. You only wish to show that it is not less effective. In this scenario, a one-tailed test would be appropriate.
When is a one-tailed test NOT appropriate?
Choosing a one-tailed test for the sole purpose of attaining significance is not appropriate. Choosing a one-tailed test after running a two-tailed test that failed to reject the null hypothesis is not appropriate, no matter how "close" to significant the two-tailed test was. Using statistical tests inappropriately can lead to invalid results that are not replicable and highly questionable–a steep price to pay for a significance star in your results table!
Deriving a one-tailed test from two-tailed output
The default among statistical packages performing tests is to report two-tailed p-values. Because the most commonly used test statistic distributions (standard normal, Student’s t) are symmetric about zero, most one-tailed p-values can be derived from the two-tailed p-values.
Below, we have the output from a two-sample t-test in Stata. The test is comparing the mean male score to the mean female score. The null hypothesis is that the difference in means is zero. The two-sided alternative is that the difference in means is not zero. There are two one-sided alternatives that one could opt to test instead: that the male score is higher than the female score (diff > 0) or that the female score is higher than the male score (diff < 0). In this instance, Stata presents results for all three alternatives. Under the headings Ha: diff < 0 and Ha: diff > 0 are the results for the one-tailed tests. In the middle, under the heading Ha: diff != 0 (which means that the difference is not equal to 0), are the results for the two-tailed test.
Two-sample t test with equal variances ------------------------------------------------------------------------------ Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval] ---------+-------------------------------------------------------------------- male | 91 50.12088 1.080274 10.30516 47.97473 52.26703 female | 109 54.99083 .7790686 8.133715 53.44658 56.53507 ---------+-------------------------------------------------------------------- combined | 200 52.775 .6702372 9.478586 51.45332 54.09668 ---------+-------------------------------------------------------------------- diff | -4.869947 1.304191 -7.441835 -2.298059 ------------------------------------------------------------------------------ Degrees of freedom: 198 Ho: mean(male) - mean(female) = diff = 0 Ha: diff < 0 Ha: diff != 0 Ha: diff > 0 t = -3.7341 t = -3.7341 t = -3.7341 P < t = 0.0001 P > |t| = 0.0002 P > t = 0.9999
Note that the test statistic, -3.7341, is the same for all of these tests. The two-tailed p-value is P > |t|. This can be rewritten as P(>3.7341) + P(< -3.7341). Because the t-distribution is symmetric about zero, these two probabilities are equal: P > |t| = 2 * P(< -3.7341). Thus, we can see that the two-tailed p-value is twice the one-tailed p-value for the alternative hypothesis that (diff < 0). The other one-tailed alternative hypothesis has a p-value of P(>-3.7341) = 1-(P<-3.7341) = 1-0.0001 = 0.9999. So, depending on the direction of the one-tailed hypothesis, its p-value is either 0.5*(two-tailed p-value) or 1-0.5*(two-tailed p-value) if the test statistic symmetrically distributed about zero.
In this example, the two-tailed p-value suggests rejecting the null hypothesis of no difference. Had we opted for the one-tailed test of (diff > 0), we would fail to reject the null because of our choice of tails.
The output below is from a regression analysis in Stata. Unlike the example above, only the two-sided p-values are presented in this output.
Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 2, 197) = 46.58 Model | 7363.62077 2 3681.81039 Prob > F = 0.0000 Residual | 15572.5742 197 79.0486001 R-squared = 0.3210 -------------+------------------------------ Adj R-squared = 0.3142 Total | 22936.195 199 115.257261 Root MSE = 8.8909 ------------------------------------------------------------------------------ socst | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- science | .2191144 .0820323 2.67 0.008 .0573403 .3808885 math | .4778911 .0866945 5.51 0.000 .3069228 .6488594 _cons | 15.88534 3.850786 4.13 0.000 8.291287 23.47939 ------------------------------------------------------------------------------
For each regression coefficient, the tested null hypothesis is that the coefficient is equal to zero. Thus, the one-tailed alternatives are that the coefficient is greater than zero and that the coefficient is less than zero. To get the p-value for the one-tailed test of the variable science having a coefficient greater than zero, you would divide the .008 by 2, yielding .004 because the effect is going in the predicted direction. This is P(>2.67). If you had made your prediction in the other direction (the opposite direction of the model effect), the p-value would have been 1 – .004 = .996. This is P(<2.67). For all three p-values, the test statistic is 2.67.
Your Name (required)
Your Email (must be a valid email for us to receive the report!)
Comment/Error Report (required)
How to cite this page
- © 2021 UC REGENTS
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Statistics and probability
Course: statistics and probability > unit 12.
- Hypothesis testing and p-values
One-tailed and two-tailed tests
- Z-statistics vs. T-statistics
- Small sample hypothesis test
- Large sample proportion hypothesis testing
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript

Hypothesis Testing for Means & Proportions
- 1
- | 2
- | 3
- | 4
- | 5
- | 6
- | 7
- | 8
- | 9
- | 10

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests
Type i and type ii errors.

All Modules

Z score Table
t score Table
The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.
- Step 1. Set up hypotheses and select the level of significance α.
H 0 : Null hypothesis (no change, no difference);
H 1 : Research hypothesis (investigator's belief); α =0.05
|
Upper-tailed, Lower-tailed, Two-tailed Tests The research or alternative hypothesis can take one of three forms. An investigator might believe that the parameter has increased, decreased or changed. For example, an investigator might hypothesize: : μ > μ , where μ is the comparator or null value (e.g., μ =191 in our example about weight in men in 2006) and an increase is hypothesized - this type of test is called an ; : μ < μ , where a decrease is hypothesized and this is called a ; or : μ ≠ μ where a difference is hypothesized and this is called a .The exact form of the research hypothesis depends on the investigator's belief about the parameter of interest and whether it has possibly increased, decreased or is different from the null value. The research hypothesis is set up by the investigator before any data are collected.
|
- Step 2. Select the appropriate test statistic.
The test statistic is a single number that summarizes the sample information. An example of a test statistic is the Z statistic computed as follows:
When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.
- Step 3. Set up decision rule.
The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.
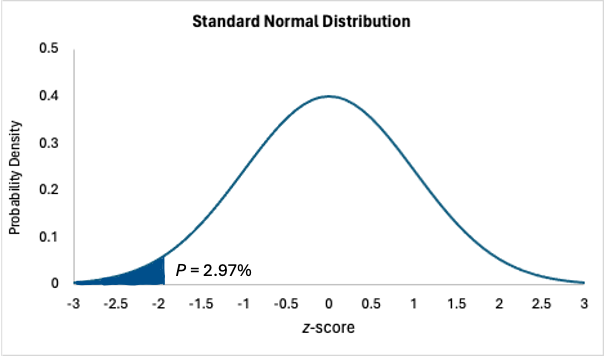
- The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value. In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
- The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.
- The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value. For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.
The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.












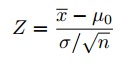








:max_bytes(150000):strip_icc():format(webp)/wk_headshot_aug_2018_02__william_kenton-5bfc261446e0fb005118afc9.jpg)
:max_bytes(150000):strip_icc():format(webp)/Term-Definitions_p-value-61f80de6ec3f4bc481ce22dac498109c.png)



COMMENTS
Two-tailed hypothesis tests are also known as nondirectional and two-sided tests because you can test for effects in both directions. When you perform a two-tailed test, you split the significance level percentage between both tails of the distribution. In the example below, I use an alpha of 5% and the distribution has two shaded regions of 2. ...
To test this, she can perform a one-tailed hypothesis test with the following null and alternative hypotheses: H 0 (Null Hypothesis): μ = 10 inches; H A (Alternative Hypothesis): μ ≠ 10 inches; This is an example of a two-tailed hypothesis test because the alternative hypothesis contains the not equal "≠" sign. The botanist believes ...
Two-Tailed Test: A two-tailed test is a statistical test in which the critical area of a distribution is two-sided and tests whether a sample is greater than or less than a certain range of values ...
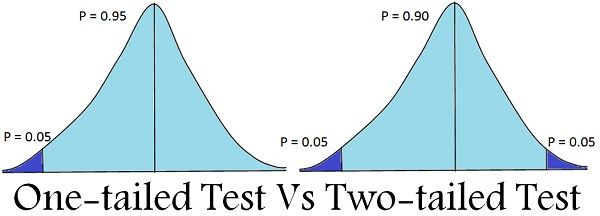
A two tailed test tells you that you're finding the area in the middle of a distribution. In other words, your rejection region (the place where you would reject the null hypothesis) is in both tails. For example, let's say you were running a z test with an alpha level of 5% (0.05). In a one tailed test, the entire 5% would be in a single tail.
In coin flipping, the null hypothesis is a sequence of Bernoulli trials with probability 0.5, yielding a random variable X which is 1 for heads and 0 for tails, and a common test statistic is the sample mean (of the number of heads) ¯. If testing for whether the coin is biased towards heads, a one-tailed test would be used - only large numbers of heads would be significant.
A two-sample t-test always uses the following null hypothesis: H 0: μ 1 = μ 2 (the two population means are equal) The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed: H 1 (two-tailed): μ 1 ≠ μ 2 (the two population means are not equal) H 1 (left-tailed): μ 1 < μ 2 (population 1 mean is less than population ...
A two-tailed test will test both if the mean is significantly greater than x and if the mean significantly less than x. ... So, depending on the direction of the one-tailed hypothesis, its p-value is either .5*(two-tailed p-value) or 1-.5*(two-tailed p-value) if the test statistic symmetrically distributed about zero.
A one tailed test does not leave more room to conclude that the alternative hypothesis is true. The benefit (increased certainty) of a one tailed test doesn't come free, as the analyst must know "something more", which is the direction of the effect, compared to a two tailed test. Show more...
The alternate hypothesis for a two-sided t-test would simply state that the mean blood pressure for the medication group is different than the placebo group, but it wouldn't specify if medication would raise or lower the mean blood pressure. Typically, researchers choose to use two-sided t-tests, since they usually don't know how a ...
So if the alternate hypothesis is written with a ≠ sign that means that we are going to perform a 2-tailed test because chances are it could be more than 100 or less than 100 which makes it 2-tailed. So, after stating the Null and Alternative hypothesis, it's time to move to step-2 which is: 2. Choose the level of Significance(α)
The two red tails are the alpha level, divided by two (i.e. α/2). Alpha levels (sometimes just called "significance levels") are used in hypothesis tests; it is the probability of making the wrong decision when the null hypothesis is true. A one-tailed test has the entire 5% of the alpha level in one tail (in either the left, or the right tail).
The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. ... In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper ...
This test is called a directional or one‐tailed test because the region of rejection is entirely within one tail of the distribution. Some hypotheses predict only that one value will be different from another, without additionally predicting which will be higher. The test of such a hypothesis is nondirectional or two‐tailed because an ...
Two-Tailed. In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t* instead of equaling -2.5.The P-value for conducting the two-tailed test H 0: μ = 3 versus H A: μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean ...
There are three different types of hypothesis tests: Two-tailed test: The alternative hypothesis contains the "≠" sign. Left-tailed test: The alternative hypothesis contains the "<" sign. Right-tailed test: The alternative hypothesis contains the ">" sign. Notice that we only have to look at the sign in the alternative hypothesis ...
A one-tailed test looks for an increase or decrease in the parameter whereas a two-tailed test looks for any change in the parameter (which can be any change- increase or decrease). We can perform the test at any level (usually 1%, 5% or 10%). For example, performing the test at a 5% level means that there is a 5% chance of wrongly rejecting H 0.
Step 2: Collect data. For a statistical test to be valid, it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in. Hypothesis testing example.
The one-tailed hypothesis is rejected only if the sample proportion is much greater than \(0.5\). The alternative hypothesis in the two-tailed test is \(\pi \neq 0.5\). In the one-tailed test it is \(\pi > 0.5\). You should always decide whether you are going to use a one-tailed or a two-tailed probability before looking at the data.
One-tailed test, as the name suggest is the statistical hypothesis test, in which the alternative hypothesis has a single end. On the other hand, two-tailed test implies the hypothesis test; wherein the alternative hypothesis has dual ends. In the one-tailed test, the alternative hypothesis is represented directionally.
HYPOTHESIS TESTING. A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the "alternate" hypothesis, and the opposite ...
For a right-tailed test: For a left-tailed test: Test Statistic: Depending on the type of test and the distribution, the test statistic is computed (Z-score for normal distribution). Decision Rule: If the test statistic falls in the critical region, reject the null hypothesis in favor of the alternative hypothesis. Example: Effect of participants of students in coding competition on their fear ...
Two tailed test. The right tailed test and the left tailed test are examples of one-tailed tests. They are called "one tailed" tests because the rejection region (the area where you would reject the null hypothesis) is only in one tail. The two tailed test is called a two tailed test because the rejection region can be in either tail.
When delving into Business Intelligence (BI), hypothesis testing is a cornerstone of data analysis, providing insights and guiding decision-making. Choosing between a one-tailed and two-tailed ...
In a one-tailed test, the entire significance level is allocated to one tail of the distribution. For example, if you are using a significance level of 0.05 (5%), you would reject the null hypothesis if your data point falls in the 5% tail on either the right (for a right-tailed test) or the left (for a left-tailed test) end of the distribution.
The formula for the two-sample t-test can be written as: Where: X 1 and X 2 are the sample means of the two groups. s 1 and s 2 are the sample variances of the two groups. n 1 and n 2 are the sample sizes of the two groups. We then need to calculate the p-value using degrees of freedom equal to (n 1 +n 2 -1).
One-Tailed Test: A one-tailed test is a statistical test in which the critical area of a distribution is one-sided so that it is either greater than or less than a certain value, but not both. If ...
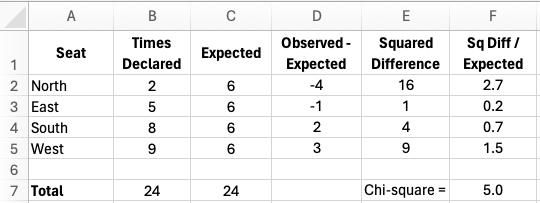
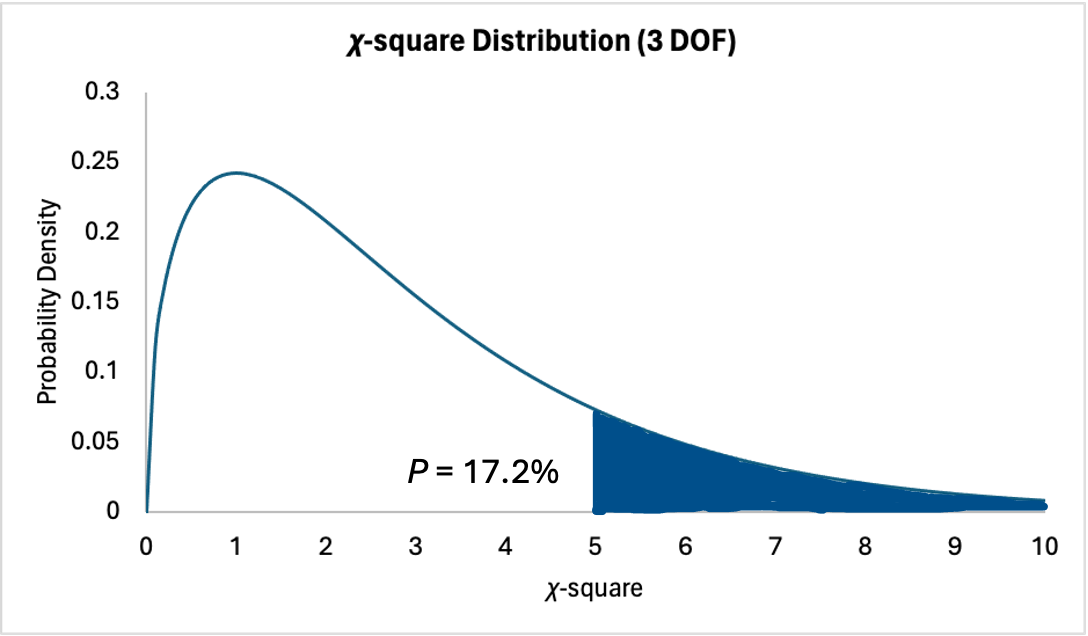
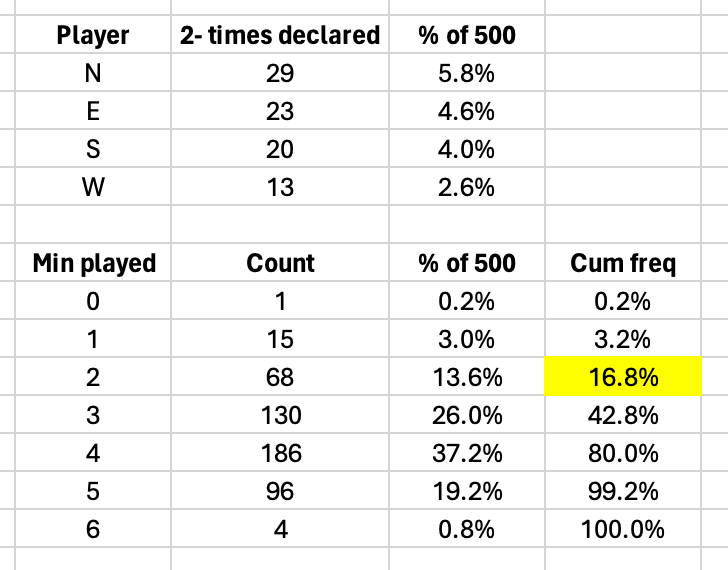
Hypothesis testing is the branch of statistical inference wherein you collect samples from a population to test an assumption about the population. In this case, the null hypothesis is that the true proportion of hands with North as declarer is 25%. The alternative hypothesis—based on our observation—is that North actually declares less ...