transportation problem solving

Transportation Problem: Finding an Optimal Solution

• Post last modified: 27 July 2022
• Reading time: 15 mins read
• Post category: Operations Research

The transportation problem is an important Linear Programming Problem (LPP). This problem depicts the transportation of goods from a group of sources to a group of destinations. The whole process is subject to the availability and demand of the sources as well as destination, respectively in a way, where entire cost of transportation is minimised.

Sometimes, it is known as Hitchcock problem. Generally, transportation costs are involved in such problems but the scope of problems extends well beyond to hide situations that do not have anything to try with these costs.

Table of Content

• 1.1 Step 1: Obtaining the Initial Feasible Solution
• 1.2 Step 2: Testing the Optimality
• 1.3 Step 3: Improving the Solution
• 2 Stepping Stone Method
• 3.1 Degeneracy in Transportation Problem
• 3.2 Unbalanced Transportation Problem
• 3.3 Alternative Optimal Solutions
• 3.4 Maximisation Transportation Problem
• 3.5 Prohibited Routes

The term ‘transportation’ is related to such problems principally because in studying efficient transportation routes, a special procedure was used which has come to be referred to as the transportation method.

A typical transportation problem is a distribution problem where transfers are made from various sources to different destinations, with known unit costs of transfer for all source-destination combinations, in a manner that the total cost of transfers is the minimum. In this chapter, you will discuss how to improve an optimal solution by stepping stone method and describe the special cases in the transportation problems.

Finding Optimal Solution Using the Stepping Stone Method

A typical transportation problem is like this. Let’s consider that a man- ufacturer of refrigerators runs three plants located at different places called A, B and C. Suppose further that his buyers are located in three regions X, Y and Z where he has got to supply them the products.

So, the need within the three regions as well as production in several plants per unit time period are known and equal in aggregate and further that the cost of one transporting refrigerator from each plant to each of the requirement centres is given and constant.

The manufacturer’s problem is to determine as to how he should route his product from his plants to the marketplaces so that the total cost involved in the transportation is minimized. In other words, he needs to decide on how many refrigerators should be supplied from A to X, Y and Z, how many from B to X, Y and Z and how many from C to X, Y and Z to attain it at the least cost.

The places where the products originate from (the plants in our example) are called the sources or the origins and places where they are to be supplied are the destinations. In this terminology, the trouble of the manufacturer is to decide on how many units are transported from different origins to different destinations in order that the overall transportation cost is the minimum.

The transportation method is an efficient alternative to the simplex method for solving transportation problems.

Step 1: Obtaining the Initial Feasible Solution

To use the transportation method is to get a feasible solution, namely, the one that satisfies the rim requirements (i.e., the requirements of demand and supply). The initial feasible solution may be obtained by various methods.

• Row Minima Method
• Column Minima Method
• North-West Corner (NWC) Rule
• Least Cost Method (LCM)
• The Vogel’s Approximation Method (VAM)

Step 2: Testing the Optimality

After obtaining the initial basic feasible solution, the successive step is to check whether it is optimal or not. There are two methods of testing the optimality of a basic feasible solution. One of these is named the stepping-stone method within which the optimality test is applied by calculating the opportunity cost of each empty cell.

The other method is named as the Modified Distribution Method (MODI). It is based on the concept of dual variables that are used to evaluate the empty cell. Using these dual variables, the opportunity cost of each of the empty cell is determined. Thus, while both methods involves determining opportunity costs of empty cells, the methodology employed by them differs.

Both the methods can be used only when the solution is a basic feasible solution so that it has m + n – 1 basic variables. If a basic feasible solution contains less than m + n – 1 non-negative allocation, then the transportation problem is said to be a degenerate one. Incidentally, none of the methods used to find initial solution would yield a solution with greater than m + n – 1 number of occupied cells.

Step 3: Improving the Solution

By applying stepping stone method, if the answer is found to be optimal, then the process terminates because the problem is solved. If the answer is not seen to be optimal, then a revised and improved basic feasible solution is obtained. This can be done by exchanging a non-basic variable for a basic variable.

In simple terms, rearrangement is formed by transferring units from an occupied cell to an empty cell that has the largest opportunity cost, then adjusting the units in other related cells in a way that each one of the rim requirements are satisfied. The solution obtained is again tested for optimality and revised, if necessary. You continue this manner until an optimal solution is finally obtained.

Stepping Stone Method

This is a procedure for determining the potential, if any, of improving upon each of the non-basic variables in terms of the objective function.

To determine this potential, each of the non-basic variables (empty cells) is taken into account one by one. For each such cell, you discover what effect on the overall cost would be if one unit is assigned to the present cell. With this information, then, you come to understand whether the solution is optimal or not.

If not, you improve that solution. This method is derived from the analogy of crossing a pond using stepping stones. It concludes that the whole transportation table is assumed to be a pond and the occupied cells are the stones required to build specific movements inside the pond.

Stepping stone method helps in determining the change in net cost by presenting any of the vacant cells into the solution. The main rule of the stepping stone method is that every increase (or decrease) in supply in one occupied cell must be associated with a decrease (or increase) in supply in another cell. The same rule also holds for demand.

The steps involved in the stepping stone method are as follows:

• Determine Initial Basic Feasible Solution (IBFS). Make sure the number of occupied cells is exactly equal to m + n − 1. 2. Evaluate the cost-effectiveness of shipping goods via transpor- tation routes for the testing of each unoccupied cell. For this, se- lect an unoccupied cell and trace a closed path using the straight route in which at least three occupied cells are used.
• Assign plus (+) and minus (−) signs alternatively in the corner cells of the closed path (identified in step 2). The unoccupied cell should be assigned with a plus sign.
• Add the unit transportation costs associated with each of the cell traced in the closed path. This would give the net change in terms of cost.
• Repeat steps 2 to 4 until all unoccupied cells are evaluated.
• Check the sign of each of the net change in the unit transportation costs. If all the net changes calculated are more than or equal to zero, an optimal solution has been attained. If not, then it is possible to advance the current solution and minimise the total transportation cost.
• Select the vacant cell with the highest negative net cost change and calculate the maximum number of units that can be assigned to this cell. The smallest value with a negative position on the closed path indicates the number of units that can be shipped to the entering cell. Add this number to the unoccupied cell and all other cells on the route having a plus sign and subtract it from the cells marked with a minus sign.
• Repeat the procedure until we get an optimal solution.

Special Cases in the Transportation Problems

Transportation is all about getting a product from one place to another, put the product on a truck or railcar and you are good to go. Well, not exactly. There’s a bit more that goes into it. It becomes particularly complicated when there are multiple places the product is coming from, and multiple places the product is going to.

Transportation managers must do to some calculations to find the optimum path for getting their product to the customer. Let us look at some common problems a transportation manager might encounter. One common transportation issue has to do with supply and demand.

Some variations that often arise while solving the transportation problem could be as follows:

Degeneracy in Transportation Problem

In a standard transportation problem with m sources of supply and n demand destinations, the test of optimality of any feasible solution requires allocations in m + n – 1 independent cells. Degeneracy occurs whenever the number of individual allocations are but m + n – 1, where m and n are the number of rows and columns of the transportation problem, respectively. Degeneracy in transportation problem can develop in two ways.

• The basic feasible solution might have been degenerate from the initial stage
• They may become degenerate at any immediate stage

To resolve degeneracy a little positive number, Δ is assigned to at least one or more unoccupied cell that have lowest transportation costs so on make N = m + n – 1 allocations. (Δ is an infinitesimally small number almost equal to zero.)

Although there is a great deal of flexibility in choosing the unused square for the Δ stone, the general procedure, when using the North West Corner Rule, is to assign it to a square in such how that it maintains an unbroken chain of stone squares. However, where Vogel’s method is used, the Δ allocation is carried during a least cost independent cell.

An independent cell during this context means a cell which cannot cause a closed path on such allocation. After this, the test of optimality is applied and if necessary, the solution is improved within the normal way until optimality is reached.

Unbalanced Transportation Problem

When the total supply of all the sources is not equal to the total demand of all destinations, the problem is an unbalanced transportation problem.

Two situations are possible: 1. If supply < demand, a dummy supply variable is introduced in the equation to make it equal to demand 2. If demand < supply, a dummy demand variable is introduced in the equation to make it equal to supply

Then before solving you must balance the demand and supply. The unit transportation cost for the dummy column and dummy row are assigned zero values, because no shipment is really made just in case of a dummy source and dummy destination.

Alternative Optimal Solutions

An alternate optimal solution is additionally called as an alternate optima, which is when a linear / integer programming problem has more than one optimal solution. Typically, an optimal solution may be a solution to a problem which satisfies the set of constraints of the problem and, therefore, the objective function which is to maximise or minimise. It is possible for a transportation problem to possess multiple optimal solutions.

This happens when one or more of the development indices zero within the optimal solution, which suggests that it’s possible to style routes with an equivalent total shipping cost. The alternate optimal solution is often found by shipping the foremost to the present unused square employing a stepping-stone path. Within the world, alternate optimal solutions provide management with greater flexibility in selecting and using resources.

Maximisation Transportation Problem

The main motive of transportation model is used to minimise transportation cost. However, it also can be used to get a solution with the objective of maximising the overall value or returns. Since the criterion of optimality is maximisation, the converse of the rule for minimisation will be used. The rule is: a solution is optimal if all – opportunity costs dij for the unoccupied cell are zero or negative.

Hence, how does all this help the business overall? If a business’ objective is to maximise profits, then finding the answer to transportation problems allows the companies to use the results from the matrixes to maximise their objective and obtain the foremost profit they will. Profit is often calculated by using this easy formula.

Profit = Selling price – Production cost – Transportation cost

If the objective of a transportation problem is to maximise profit, a minor change is required in the transportation algorithm. Now, the optimal solution is reached when all the development indices are negative or zero. The cell with the most important positive improvement index is chosen to be filled by employing a stepping-stone path. This new solution is evaluated and therefore the process continues until there are not any positive improvement indices.

Prohibited Routes

At times there is transportation problems during which one among the sources is unable to ship to at least one or more of the destinations. When this happens, the problem is claimed to have an unacceptable or prohibited route.

In a minimisation problem, such a prohibited route is assigned a really high cost to prevent this route from ever getting used within the optimal solution. In a maximisation problem, the very high cost utilised in minimisation problems is given a negative sign, turning it into an awfully bad profit.

Sometimes there could also be situations, where it is unacceptable to use certain routes during a transportation problem. For example, road construction, bad road conditions, strike, unexpected floods, local traffic rules, etc.

Such restrictions (or prohibitions) will be handled within the transportation problem by assigning a very high cost (say M or [infinity]) to the prohibited routes to make sure that routes will not be included within the optimal solution then the matter is solved within the usual manner.

Business Ethics

( Click on Topic to Read )

• What is Ethics?
• What is Business Ethics?
• Values, Norms, Beliefs and Standards in Business Ethics
• Indian Ethos in Management
• Ethical Issues in Marketing
• Ethical Issues in HRM
• Ethical Issues in IT
• Ethical Issues in Production and Operations Management
• Ethical Issues in Finance and Accounting
• What is Corporate Governance?
• What is Ownership Concentration?
• What is Ownership Composition?
• Types of Companies in India
• Internal Corporate Governance
• External Corporate Governance
• Corporate Governance in India
• What is Enterprise Risk Management (ERM)?
• What is Assessment of Risk?
• What is Risk Register?
• Risk Management Committee

Corporate social responsibility (CSR)

• Theories of CSR
• Arguments Against CSR
• Business Case for CSR
• Importance of CSR in India
• Drivers of Corporate Social Responsibility
• Developing a CSR Strategy
• Implement CSR Commitments
• CSR Marketplace
• CSR at Workplace
• Environmental CSR
• CSR with Communities and in Supply Chain
• Community Interventions
• CSR Monitoring
• CSR Reporting
• Voluntary Codes in CSR
• What is Corporate Ethics?

Lean Six Sigma

• What is Six Sigma?
• What is Lean Six Sigma?
• Value and Waste in Lean Six Sigma
• Six Sigma Team
• MAIC Six Sigma
• Six Sigma in Supply Chains
• What is Binomial, Poisson, Normal Distribution?
• What is Sigma Level?
• What is DMAIC in Six Sigma?
• What is DMADV in Six Sigma?
• Six Sigma Project Charter
• Project Decomposition in Six Sigma
• Critical to Quality (CTQ) Six Sigma
• Process Mapping Six Sigma
• Flowchart and SIPOC
• Gage Repeatability and Reproducibility
• Statistical Diagram
• Lean Techniques for Optimisation Flow
• Failure Modes and Effects Analysis (FMEA)
• What is Process Audits?
• Six Sigma Implementation at Ford
• IBM Uses Six Sigma to Drive Behaviour Change
• Research Methodology
• What is Research?
• What is Hypothesis?
• Sampling Method
• Research Methods
• Data Collection in Research
• Methods of Collecting Data
• Application of Business Research
• Levels of Measurement
• What is Sampling?
• Hypothesis Testing
• Research Report
• What is Management?
• Planning in Management
• Decision Making in Management
• What is Controlling?
• What is Coordination?
• What is Staffing?
• Organization Structure
• What is Departmentation?
• Span of Control
• What is Authority?
• Centralization vs Decentralization
• Organizing in Management
• Schools of Management Thought
• Classical Management Approach
• Is Management an Art or Science?
• Who is a Manager?

Operations Research

• What is Operations Research?
• Operation Research Models
• Linear Programming
• Linear Programming Graphic Solution
• Linear Programming Simplex Method
• Linear Programming Artificial Variable Technique

Duality in Linear Programming

• Transportation Problem Initial Basic Feasible Solution
• Transportation Problem Finding Optimal Solution
• Project Network Analysis with Critical Path Method

Project Network Analysis Methods

Project evaluation and review technique (pert), simulation in operation research.

• Replacement Models in Operation Research

Operation Management

• What is Strategy?
• What is Operations Strategy?
• Operations Competitive Dimensions
• Operations Strategy Formulation Process
• What is Strategic Fit?
• Strategic Design Process
• Focused Operations Strategy
• Corporate Level Strategy
• Expansion Strategies
• Stability Strategies
• Retrenchment Strategies
• Competitive Advantage
• Strategic Choice and Strategic Alternatives
• What is Production Process?
• What is Process Technology?
• What is Process Improvement?
• Strategic Capacity Management
• Production and Logistics Strategy
• Taxonomy of Supply Chain Strategies
• Factors Considered in Supply Chain Planning
• Operational and Strategic Issues in Global Logistics
• Logistics Outsourcing Strategy
• What is Supply Chain Mapping?
• Supply Chain Process Restructuring
• Points of Differentiation
• Re-engineering Improvement in SCM
• What is Supply Chain Drivers?
• Supply Chain Operations Reference (SCOR) Model
• Customer Service and Cost Trade Off
• Internal and External Performance Measures
• Linking Supply Chain and Business Performance
• Netflix’s Niche Focused Strategy
• Disney and Pixar Merger
• Process Planning at Mcdonald’s

Service Operations Management

• What is Service?
• What is Service Operations Management?
• What is Service Design?
• Service Design Process
• Service Delivery
• What is Service Quality?
• Gap Model of Service Quality
• Juran Trilogy
• Service Performance Measurement
• Service Decoupling
• IT Service Operation
• Service Operations Management in Different Sector

Procurement Management

• What is Procurement Management?
• Procurement Negotiation
• Types of Requisition
• RFX in Procurement
• What is Purchasing Cycle?
• Vendor Managed Inventory
• Internal Conflict During Purchasing Operation
• Spend Analysis in Procurement
• Sourcing in Procurement
• Supplier Evaluation and Selection in Procurement
• Blacklisting of Suppliers in Procurement
• Total Cost of Ownership in Procurement
• Incoterms in Procurement
• Documents Used in International Procurement
• Transportation and Logistics Strategy
• What is Capital Equipment?
• Procurement Process of Capital Equipment
• Acquisition of Technology in Procurement
• What is E-Procurement?
• E-marketplace and Online Catalogues
• Fixed Price and Cost Reimbursement Contracts
• Contract Cancellation in Procurement
• Ethics in Procurement
• Legal Aspects of Procurement
• Global Sourcing in Procurement
• Intermediaries and Countertrade in Procurement

Strategic Management

• What is Strategic Management?
• What is Value Chain Analysis?
• Mission Statement
• Business Level Strategy
• What is SWOT Analysis?
• What is Competitive Advantage?
• What is Vision?
• What is Ansoff Matrix?
• Prahalad and Gary Hammel
• Strategic Management In Global Environment
• Competitor Analysis Framework
• Competitive Rivalry Analysis
• Competitive Dynamics
• What is Competitive Rivalry?
• Five Competitive Forces That Shape Strategy
• What is PESTLE Analysis?
• Fragmentation and Consolidation Of Industries
• What is Technology Life Cycle?
• What is Diversification Strategy?
• What is Corporate Restructuring Strategy?
• Resources and Capabilities of Organization
• Role of Leaders In Functional-Level Strategic Management
• Functional Structure In Functional Level Strategy Formulation
• Information And Control System
• What is Strategy Gap Analysis?
• Issues In Strategy Implementation
• Matrix Organizational Structure
• What is Strategic Management Process?

Supply Chain

• What is Supply Chain Management?
• Supply Chain Planning and Measuring Strategy Performance
• What is Warehousing?
• What is Packaging?
• What is Inventory Management?
• What is Material Handling?
• What is Order Picking?
• Receiving and Dispatch, Processes
• What is Warehouse Design?
• What is Warehousing Costs?

You Might Also Like

What is linear programming assumptions, properties, advantages, disadvantages, transportation problem: initial basic feasible solution, linear programming: simplex method, linear programming: graphic solution, linear programming: artificial variable technique, what is operations research (or) definition, concept, characteristics, tools, advantages, limitations, applications and uses, operation research models and modelling, project network analysis with critical path method, leave a reply cancel reply.

You must be logged in to post a comment.

World's Best Online Courses at One Place

We’ve spent the time in finding, so you can spend your time in learning

Digital Marketing

Personal growth.

Development

All Courses

• Interview Questions
• Free Courses
• Career Guide
• PGP in Data Science and Business Analytics
• PG Program in Data Science and Business Analytics Classroom
• PGP in Data Science and Engineering (Data Science Specialization)
• PGP in Data Science and Engineering (Bootcamp)
• PGP in Data Science & Engineering (Data Engineering Specialization)
• Master of Data Science (Global) – Deakin University
• MIT Data Science and Machine Learning Course Online
• Master’s (MS) in Data Science Online Degree Programme
• MTech in Data Science & Machine Learning by PES University
• Data Analytics Essentials by UT Austin
• Data Science & Business Analytics Program by McCombs School of Business
• MTech In Big Data Analytics by SRM
• M.Tech in Data Engineering Specialization by SRM University
• M.Tech in Big Data Analytics by SRM University
• PG in AI & Machine Learning Course
• Weekend Classroom PG Program For AI & ML
• AI for Leaders & Managers (PG Certificate Course)
• Artificial Intelligence Course for School Students
• IIIT Delhi: PG Diploma in Artificial Intelligence
• Machine Learning PG Program
• MIT No-Code AI and Machine Learning Course
• Study Abroad: Masters Programs
• MS in Information Science: Machine Learning From University of Arizon
• SRM M Tech in AI and ML for Working Professionals Program
• UT Austin Artificial Intelligence (AI) for Leaders & Managers
• UT Austin Artificial Intelligence and Machine Learning Program Online
• MS in Machine Learning
• IIT Roorkee Full Stack Developer Course
• IIT Madras Blockchain Course (Online Software Engineering)
• IIIT Hyderabad Software Engg for Data Science Course (Comprehensive)
• IIIT Hyderabad Software Engg for Data Science Course (Accelerated)
• IIT Bombay UX Design Course – Online PG Certificate Program
• Online MCA Degree Course by JAIN (Deemed-to-be University)
• Cybersecurity PG Course
• Online Post Graduate Executive Management Program
• Product Management Course Online in India
• NUS Future Leadership Program for Business Managers and Leaders
• PES Executive MBA Degree Program for Working Professionals
• Online BBA Degree Course by JAIN (Deemed-to-be University)
• MBA in Digital Marketing or Data Science by JAIN (Deemed-to-be University)
• Master of Business Administration- Shiva Nadar University
• Post Graduate Diploma in Management (Online) by Great Lakes
• Online MBA Programs
• Cloud Computing PG Program by Great Lakes
• University Programs
• Stanford Design Thinking Course Online
• Design Thinking : From Insights to Viability
• PGP In Strategic Digital Marketing
• Post Graduate Diploma in Management
• Master of Business Administration Degree Program
• MS in Business Analytics in USA
• MS in Machine Learning in USA
• Study MBA in Germany at FOM University
• M.Sc in Big Data & Business Analytics in Germany
• Study MBA in USA at Walsh College
• MS Data Analytics
• MS Artificial Intelligence and Machine Learning
• MS in Data Analytics
• Master of Business Administration (MBA)
• MS in Information Science: Machine Learning
• MS in Machine Learning Online
• MIT Data Science Program
• AI For Leaders Course
• Data Science and Business Analytics Course
• Cyber Security Course
• PG Program Online Artificial Intelligence Machine Learning
• PG Program Online Cloud Computing Course
• Data Analytics Essentials Online Course
• MIT Programa Ciencia De Dados Machine Learning
• MIT Programa Ciencia De Datos Aprendizaje Automatico
• Program PG Ciencia Datos Analitica Empresarial Curso Online
• Mit Programa Ciencia De Datos Aprendizaje Automatico
• Online Data Science Business Analytics Course
• Online Ai Machine Learning Course
• Online Full Stack Software Development Course
• Online Cloud Computing Course
• Cybersecurity Course Online
• Online Data Analytics Essentials Course
• Ai for Business Leaders Course
• Mit Data Science Program
• No Code Artificial Intelligence Machine Learning Program
• MS Information Science Machine Learning University Arizona
• Wharton Online Advanced Digital Marketing Program
• Introduction

Transportation Problem Explained and how to solve it?

• Transportation Problem
• Balanced Problem
• Unbalanced Problem

Contributed by: Patrick

Operations Research (OR) is a state of art approach used for problem-solving and decision making. OR helps any organization to achieve their best performance under the given constraints or circumstances. The prominent OR techniques are,

• Linear programming
• Goal programming
• Integer programming
• Dynamic programming
• Network programming

One of the problems the organizations face is the transportation problem. It originally means the problem of transporting/shipping the commodities from the industry to the destinations with the least possible cost while satisfying the supply and demand limits.  It is a special class of linear programming technique that was designed for models with linear objective and constraint functions. Their application can be extended to other areas of operation, including

• Scheduling and Time management
• Network optimization
• Inventory management
• Enterprise resource planning
• Process planning
• Routing optimization  

The notations of the representation are:

m sources and n destinations

(i , j) joining source (i) and destination (j)

c ij 🡪  transportation cost per unit

x ij 🡪  amount shipped

a i   🡪 the amount of supply at source (i)

b j   🡪 the amount of demand at destination (j)

Transportation problem works in a way of minimizing the cost function. Here, the cost function is the amount of money spent to the logistics provider for transporting the commodities from production or supplier place to the demand place. Many factors decide the cost of transport. It includes the distance between the two locations, the path followed, mode of transport, the number of units that are transported, the speed of transport, etc. So, the focus here is to transport the commodities with minimum transportation cost without any compromise in supply and demand. The transportation problem is an extension of linear programming technique because the transportation costs are formulated as a linear function to the supply capacity and demand. Check out the course on transportation analytics .

Transportation problem exists in two forms. 

• Balanced 

It is the case where the total supply equals the total demand.

It is the case where either the demand is greater than the supply, or vice versa.

In most cases, the problems take a balanced form. It is because usually, the production units work, taking the inventory and the demand into consideration. Overproduction increases the inventory cost whereas under production is challenged by the demand. Hence the trade-off should be carefully examined. Whereas, the unbalanced form exists in a situation where there is an unprecedented increase or decrease in demand.

Let us understand this in a much simpler way with the help of a basic example. 

Let us assume that there is a leading global automotive supplier company named JIM. JIM has it’s production plants in many countries and supplies products to all the top automotive makers in the world. For instance, let’s consider that there are three plants in India at places M, N, and O. The capacity of the plants is 700, 300, 550 per day. The plant supplies four customers A, B, C, and D, whose demand is 650, 200, 450, 250 per day. The cost of transport per unit per km in INR and the distance between each source and destination in Kms are given in the tables below.

Here, the objective is to determine the unknown while satisfying all the supply and demand restrictions. The cost of shipping from a source to a destination is directly proportional to the number of units shipped.

Many sophisticated programming languages have evolved to solve OR problems in a much simpler and easier way. But the significance of Microsoft Excel cannot be compromised and devalued at any time. It also provides us with a greater understanding of the problem than others. Hence we will use Excel to solve the problem.

It is always better to formulate the working procedure in steps that it helps in better understanding and prevents from committing any error.

Steps to be followed to solve the problem:

• Create a transportation matrix (define decision variables)
• Define the objective function
• Formulate the constraints
• Solve using LP method 

Creating a transportation matrix:

A transportation matrix is a way of understanding the maximum possibilities the shipment can be done. It is also known as decision variables because these are the variables of interest that we will change to achieve the objective, that is, minimizing the cost function.

Define the objective function: 

An objective function is our target variable. It is the cost function, that is, the total cost incurred for transporting. It is known as an objective function because our interest here is to minimize the cost of transporting while satisfying all the supply and demand restrictions.

The objective function is the total cost. It is obtained by the sum product of the cost per unit per km and the decision variables (highlighted in red), as the total cost is directly proportional to the sum product of the number of units shipped and cost of transport per unit per Km.

The column “Total shipped” is the sum of the columns A, B, C, and D for respective rows and the row “Total Demand” is the sum of rows M, N, and O for the respective columns. These two columns are introduced to satisfy the constraints of the amount of supply and demand while solving the cost function. 

Formulate the constraints:

The constraints are formulated concerning the demand and supply for respective rows and columns. The importance of these constraints is to ensure they satisfy all the supply and demand restrictions.

For example, the fourth constraint, x ma + x na + x oa = 650 is used to ensure that the number of units coming from plants M, N, and O to customer A should not go below or above the demand that A has. Similarly the first constraint x ma + x mb + x mc + x md  = 700 will ensure that the capacity of the plant M will not go below or above the given capacity hence, the plant can be utilized to its fullest potential without compromising the inventory. 

Solve using LP method:

The simplest and most effective method to solve is using solver. The input parameters are fed as stated below and proceed to solve. 

This is the best-optimized cost function, and there is no possibility to achieve lesser cost than this having the same constraints.

From the solved solution, it is seen that plant M ships 100 units to customer A, 350 units to C and 250 units to D. But why nothing to customer B? And a similar trend can be seen for other plants as well. 

What could be the reason for this? Yes, you guessed it right! It is because some other plants ship at a profitable rate to a customer than others and as a result, you can find few plants supplying zero units to certain customers. 

So, when will these zero unit suppliers get profitable and can supply to those customers? Wait! Don’t panic. Excel has got away for it too. After proceeding to solve, there appears a dialogue box in which select the sensitivity report and click OK. You will get a wonderful sensitivity report which gives details of the opportunity cost or worthiness of the resource.

Basic explanation for the report variables,

Cell: The cell ID in the excel

Name: The supplier customer pairing

Final value: Number of units shipped (after solving)

Reduced cost: How much should the transportation cost per unit per km should be reduced to make the zero supplying plant profitable and start supplying

Objective coefficient: Current transportation cost per unit per Km for each supplier customer pair

Allowable Increase: It tells us the maximum cost of the current transportation cost per unit per Km can be increased which doesn’t make any changes to the solution

Allowable Decrease: It tells how much maximum the current transportation cost per unit per Km can be lowered which doesn’t make any changes to the solution

Here, look into the first row of the sensitivity report. Plant M supplies to customer A. Here, the transportation cost per unit per Km is ₹14 and 100 units are shipped to customer A. In this case, the transportation cost can increase a maximum of ₹6, and can lower to a maximum of ₹1. For any value within this range, there will not be any change in the final solution. 

Now, something interesting. Look at the second row. Between MB, there is not a single unit supplied to customer B from plant M. The current shipping cost is ₹22 and to make this pair profitable and start a business, the cost should come down by ₹6 per unit per Km. Whereas, there is no possibility of increasing the cost by even a rupee. If the shipping cost for this pair comes down to ₹16, we can expect a business to begin between them, and the final solution changes accordingly.

The above example is a balanced type problem where the supply equals the demand. In case of an unbalanced type, a dummy variable is added with either a supplier or a customer based on how the imbalance occurs.

Thus, the transportation problem in Excel not only solves the problem but also helps us to understand how the model works and what can be changed, and to what extent to modify the solution which in turn helps to determine the cost and an optimal supplier. 

If you found this helpful, and wish to learn more such concepts, head over to Great Learning Academy and enroll in the free online courses today.

Top Free Courses

What is Time Complexity And Why Is It Essential?

Top 30 Python Libraries To Know

Python Dictionary Append: How To Add Key/Value Pair?

¿Qué es la Ciencia de Datos? – Una Guía Completa [2024]

What is Data Science? – The Complete Guide

Python NumPy Tutorial – 2024

Leave a comment cancel reply.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Table of contents

• MapReduce Algorithm
• Linear Programming using Pyomo
• Networking and Professional Development for Machine Learning Careers in the USA
• Predicting Employee Churn in Python
• Airflow Operators

Solving Transportation Problem using Linear Programming in Python

Learn how to use Python PuLP to solve transportation problems using Linear Programming.

In this tutorial, we will broaden the horizon of linear programming problems. We will discuss the Transportation problem. It offers various applications involving the optimal transportation of goods. The transportation model is basically a minimization model.

The transportation problem is a type of Linear Programming problem. In this type of problem, the main objective is to transport goods from source warehouses to various destination locations at minimum cost. In order to solve such problems, we should have demand quantities, supply quantities, and the cost of shipping from source and destination. There are m sources or origin and n destinations, each represented by a node. The edges represent the routes linking the sources and the destinations.

In this tutorial, we are going to cover the following topics:

Transportation Problem

The transportation models deal with a special type of linear programming problem in which the objective is to minimize the cost. Here, we have a homogeneous commodity that needs to be transferred from various origins or factories to different destinations or warehouses.

Types of Transportation problems

• Balanced Transportation Problem :  In such type of problem, total supplies and demands are equal.
• Unbalanced Transportation Problem : In such type of problem, total supplies and demands are not equal.

Methods for Solving Transportation Problem:

• NorthWest Corner Method
• Least Cost Method
• Vogel’s Approximation Method (VAM)

Let’s see one example below. A company contacted the three warehouses to provide the raw material for their 3 projects.

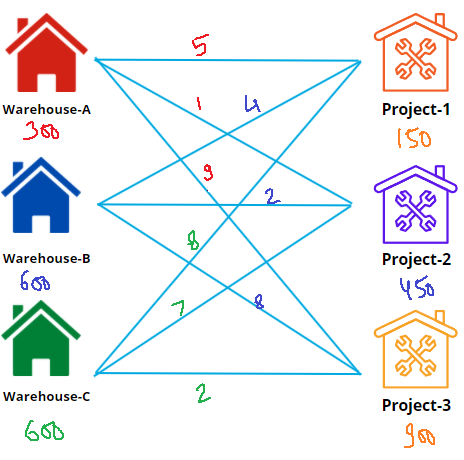
This constitutes the information needed to solve the problem. The next step is to organize the information into a solvable transportation problem.

Formulate Problem

Let’s first formulate the problem. first, we define the warehouse and its supplies, the project and its demands, and the cost matrix.

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have various Route variables. Let’s create them using  LpVariable.dicts()  class.  LpVariable.dicts()  used with Python’s list comprehension.  LpVariable.dicts()  will take the following four values:

• First, prefix name of what this variable represents.
• Second is the list of all the variables.
• Third is the lower bound on this variable.
• Fourth variable is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are  LpContinuous  or  LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem  object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

In this code, we have summed up the two variables(full-time and part-time) list values in an additive fashion.

Define the Constraints

Here, we are adding two types of constraints: supply maximum constraints and demand minimum constraints. We have added the 4 constraints defined in the problem by adding them to the LpProblem  object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Warehouse-A supplies the 300 units to Project -2. Warehouse-B supplies 150, 150, and 300 to respective project sites. And finally, Warehouse-C supplies 600 units to Project-3.

In this article, we have learned about Transportation problems, Problem Formulation, and implementation using the python PuLp library. We have solved the transportation problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. In upcoming articles, we will write more on different optimization problems such as transshipment problem, assignment problem, balanced diet problem. You can revise the basics of mathematical concepts in  this article  and learn about Linear Programming  in this article .

• Solving Cargo Loading Problem using Integer Programming in Python
• Solving Blending Problem in Python using Gurobi

You May Also Like

Dimensionality Reduction using PCA

Sensitivity Analysis in Python

Naive Bayes Classification using Scikit-learn

• Practice Mathematical Algorithm
• Mathematical Algorithms
• Pythagorean Triplet
• Fibonacci Number
• Euclidean Algorithm
• LCM of Array
• GCD of Array
• Binomial Coefficient
• Catalan Numbers
• Sieve of Eratosthenes
• Euler Totient Function
• Modular Exponentiation
• Modular Multiplicative Inverse
• Stein's Algorithm
• Juggler Sequence
• Chinese Remainder Theorem
• Quiz on Fibonacci Numbers
• Transportation Problem | Set 6 (MODI Method - UV Method)
• Transportation Problem | Set 2 (NorthWest Corner Method)
• Transportation Problem | Set 4 (Vogel's Approximation Method)
• Transportation Problem | Set 1 (Introduction)
• Transportation Problem | Set 3 (Least Cost Cell Method)
• Transportation Problem Set 8 | Transshipment Model-1
• Transportation Problem | Set 5 ( Unbalanced )
• Transportation Problem | Set 7 ( Degeneracy in Transportation Problem )
• Travelling Salesman Problem using Hungarian method
• Travelling Salesman Problem (TSP) using Reduced Matrix Method
• Traveling Salesman Problem (TSP) Implementation
• Approximate solution for Travelling Salesman Problem using MST
• Travelling Salesman Problem implementation using BackTracking
• Bitonic Travelling Salesman Problem
• Bellman Ford Algorithm (Simple Implementation)
• Find the minimum cost to reach destination using a train
• Problem on Trains, Boat and streams
• Java Program to Solve Travelling Salesman Problem Using Incremental Insertion Method
• QA - Placement Quizzes | Mixtures and Alligation | Question 6
• QA - Placement Quizzes | Permutation and Combination | Question 8

Transportation Problem | Set 6 (MODI Method – UV Method)

There are two phases to solve the transportation problem. In the first phase, the initial basic feasible solution has to be found and the second phase involves optimization of the initial basic feasible solution that was obtained in the first phase. There are three methods for finding an initial basic feasible solution,

NorthWest Corner Method

• Least Cost Cell Method
• Vogel’s Approximation Method

This article will discuss how to optimize the initial basic feasible solution through an explained example. Consider the below transportation problem.

Check whether the problem is balanced or not. If the total sum of all the supply from sources

is equal to the total sum of all the demands for destinations

then the transportation problem is a balanced transportation problem.

If the problem is not unbalanced then the concept of a dummy row or a dummy column to transform the unbalanced problem to balanced can be followed as discussed in

Finding the initial basic feasible solution. Any of the three aforementioned methods can be used to find the initial basic feasible solution. Here,

will be used. And according to the NorthWest Corner Method this is the final initial basic feasible solution:

Now, the total cost of transportation will be

(200 * 3) + (50 * 1) + (250 * 6) + (100 * 5) + (250 * 3) + (150 * 2) = 3700

U-V method to optimize the initial basic feasible solution. The following is the initial basic feasible solution:

– For U-V method the values

have to be found for the rows and the columns respectively. As there are three rows so three

values have to be found i.e.

for the first row,

for the second row and

for the third row. Similarly, for four columns four

. Check the image below:

There is a separate formula to find

is the cost value only for the allocated cell. Read more about it

. Before applying the above formula we need to check whether

m + n – 1 is equal to the total number of allocated cells

or not where

is the total number of rows and

is the total number of columns. In this case m = 3, n = 4 and total number of allocated cells is 6 so m + n – 1 = 6. The case when m + n – 1 is not equal to the total number of allocated cells will be discussed in the later posts. Now to find the value for u and v we assign any of the three u or any of the four v as 0. Let we assign

in this case. Then using the above formula we will get

). Similarly, we have got the value for

so we get the value for

which implies

. From the value of

. See the image below:

Now, compute penalties using the formula

only for unallocated cells. We have two unallocated cells in the first row, two in the second row and two in the third row. Lets compute this one by one.

• For C 13 , P 13 = 0 + 0 – 7 = -7 (here C 13 = 7 , u 1 = 0 and v 3 = 0 )
• For C 14 , P 14 = 0 + (-1) -4 = -5
• For C 21 , P 21 = 5 + 3 – 2 = 6
• For C 24 , P 24 = 5 + (-1) – 9 = -5
• For C 31 , P 31 = 3 + 3 – 8 = -2
• For C 32 , P 32 = 3 + 1 – 3 = 1

If we get all the penalties value as zero or negative values that mean the optimality is reached and this answer is the final answer. But if we get any positive value means we need to proceed with the sum in the next step. Now find the maximum positive penalty. Here the maximum value is 6 which corresponds to

cell. Now this cell is new basic cell. This cell will also be included in the solution.

The rule for drawing closed-path or loop.

Starting from the new basic cell draw a closed-path in such a way that the right angle turn is done only at the allocated cell or at the new basic cell. See the below images:

Assign alternate plus-minus sign to all the cells with right angle turn (or the corner) in the loop with plus sign assigned at the new basic cell.

Consider the cells with a negative sign. Compare the allocated value (i.e. 200 and 250 in this case) and select the minimum (i.e. select 200 in this case). Now subtract 200 from the cells with a minus sign and add 200 to the cells with a plus sign. And draw a new iteration. The work of the loop is over and the new solution looks as shown below.

Check the total number of allocated cells is equal to (m + n – 1). Again find u values and v values using the formula

is the cost value only for allocated cell. Assign

then we get

. Similarly, we will get following values for

Find the penalties for all the unallocated cells using the formula

• For C 11 , P 11 = 0 + (-3) – 3 = -6
• For C 13 , P 13 = 0 + 0 – 7 = -7
• For C 14 , P 14 = 0 + (-1) – 4 = -5
• For C 31 , P 31 = 0 + (-3) – 8 = -11

There is one positive value i.e. 1 for

. Now this cell becomes new basic cell.

Now draw a loop starting from the new basic cell. Assign alternate plus and minus sign with new basic cell assigned as a plus sign.

Select the minimum value from allocated values to the cell with a minus sign. Subtract this value from the cell with a minus sign and add to the cell with a plus sign. Now the solution looks as shown in the image below:

Check if the total number of allocated cells is equal to (m + n – 1). Find u and v values as above.

Now again find the penalties for the unallocated cells as above.

• For P 11 = 0 + (-2) – 3 = -5
• For P 13 = 0 + 1 – 7 = -6
• For P 14 = 0 + 0 – 4 = -4
• For P 22 = 4 + 1 – 6 = -1
• For P 24 = 4 + 0 – 9 = -5
• For P 31 = 2 + (-2) – 8 = -8

All the penalty values are negative values. So the optimality is reached. Now, find the total cost i.e.

(250 * 1) + (200 * 2) + (150 * 5) + (50 * 3) + (200 * 3) + (150 * 2) = 2450

Please Login to comment...

Similar reads.

• Mathematical

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Balanced and Unbalanced Transportation Problems

The two categories of transportation problems are balanced and unbalanced transportation problems . As we all know, a transportation problem is a type of Linear Programming Problem (LPP) in which items are carried from a set of sources to a set of destinations based on the supply and demand of the sources and destinations, with the goal of minimizing the total transportation cost. It is also known as the Hitchcock problem.

Introduction to Balanced and Unbalanced Transportation Problems

Balanced transportation problem.

The problem is considered to be a balanced transportation problem when both supplies and demands are equal.

Unbalanced Transportation Problem

Unbalanced transportation problem is defined as a situation in which supply and demand are not equal. A dummy row or a dummy column is added to this type of problem, depending on the necessity, to make it a balanced problem. The problem can then be addressed in the same way as the balanced problem.

Methods of Solving Transportation Problems

There are three ways for determining the initial basic feasible solution. They are

1. NorthWest Corner Cell Method.

2. Vogel’s Approximation Method (VAM).

3. Least Call Cell Method.

The following is the basic framework of the balanced transportation problem:

The destinations D1, D2, D3, and D4 in the above table are where the products/goods will be transported from various sources O1, O2, O3, and O4. The supply from the source Oi is represented by S i . The demand for the destination Dj is d j . If a product is delivered from source Si to destination Dj, then the cost is called C ij .

Let us now explore the process of solving the balanced transportation problem using one of the ways known as the NorthWest Corner Method in this article.

Solving Balanced Transportation problem by Northwest Corner Method

Consider this scenario:

With three sources (O1, O2, and O3) and four destinations (D1, D2, D3, and D4), what is the best way to solve this problem? The supply for the sources O1, O2, and O3 are 300, 400, and 500, respectively. Demands for the destination D1, D2, D3, and D4 are 250, 350, 400, and 200, respectively.

The starting point for the North West Corner technique is (O1, D1), which is the table’s northwest corner. The cost of transportation is calculated for each value in the cell. As indicated in the diagram, compare the demand for column D1 with the supply from source O1 and assign a minimum of two to the cell (O1, D1).

Column D1’s demand has been met, hence the entire column will be canceled. The supply from the source O1 is still 300 – 250 = 50.

Analyze the northwest corner, i.e. (O1, D2), of the remaining table, excluding column D1, and assign the lowest among the supply for the appropriate column and rows. Because the supply from O1 is 50 and the demand for D2 is 350, allocate 50 to the cell (O1, D2).

Now, row O1 is canceled because the supply from row O1 has been completed. Hence, the demand for Column D2 has become 350 – 50 = 50.

The northwest corner cell in the remaining table is (O2, D2). The shortest supply from source O2 (400) and the demand for column D2 (300) is 300, thus putting 300 in the cell (O2, D2). Because the demand for column D2 has been met, the column can be deleted, and the remaining supply from source O2 is 400 – 300 = 100.

Again, find the northwest corner of the table, i.e. (O2, D3), and compare the O2 supply (i.e. 100) to the D2 demand (i.e. 400) and assign the smaller (i.e. 100) to the cell (O2, D2). Row O2 has been canceled because the supply from O2 has been completed. Column D3 has a leftover demand of 400 – 100 = 300.

Continuing in the same manner, the final cell values will be:

It should be observed that the demand for the relevant columns and rows is equal in the last remaining cell, which was cell (O3, D4). In this situation, the supply from O3 was 200, and the demand for D4 was 200, therefore this cell was assigned to it. Nothing was left for any row or column at the end.

To achieve the basic solution, multiply the allotted value by the respective cell value (i.e. the cost) and add them all together.

I.e., (250 × 3) + (50 × 1) + (300 × 6) + (100 × 5) + (300 × 3) + (200 × 2) = 4400.

Solving Unbalanced Transportation Problem

An unbalanced transportation problem is provided below. Because the sum of all the supplies, O1, O2, O3, and O4, does not equal the sum of all the demands, D1, D2, D3, D4, and D5, the situation is unbalanced.

The idea of a dummy row or dummy column will be applied in this type of scenario. Because the supply is more than the demand in this situation, a fake demand column will be inserted, with a demand of (total supply – total demand), i.e. 117 – 95 = 22, as seen in the image below. A fake supply row would have been introduced if demand was greater than supply.

Now this problem has been changed to a balanced transportation problem, and it can be addressed using any of the ways listed below to solve a balanced transportation problem, such as the northwest corner method mentioned earlier.

Frequently Asked Questions on Balanced and Unbalanced Transportation Problems

What is meant by balanced and unbalanced transportation problems.

The problem is referred to as a balanced transportation problem when both supplies and demands are equal. Unbalanced transportation is defined as a situation where supply and demand are not equal.

What is called a transportation problem?

The transportation problem is a type of Linear Programming Problem in which commodities are carried from a set of sources to a set of destinations while taking into account the supply and demand of the sources and destinations, respectively, in order to reduce the total cost of transportation.

What are the different methods to solve transportation problems?

The following are three approaches to solve the transportation issue:

• NorthWest Corner Cell Method.
• Least Call Cell Method.
• Vogel’s Approximation Method (VAM).

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey

Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

WHAT IS TRANSPORTATION PROBLEM

The transportation problem is a special type of linear programming problem where the objective is to minimise the cost of distributing a product from a number of sources or origins to a number of destinations. Because of its special structure the usual simplex method is not suitable for solving transportation problems. These problems require a special method of solution. The origin of a transportation problem is the location from which shipments are despatched. The destination of a transportation problem is the location to which shipments are transported. The unit transportation cost is the cost of transporting one unit of the consignment from an origin to a destination.

In the most general form, a transportation ...

Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

A Comprehensive Literature Review on Transportation Problems

• Review Article
• Published: 24 September 2021
• Volume 7 , article number  206 , ( 2021 )

Cite this article

• Yadvendra Kacher 1 &
• Pitam Singh 1  

841 Accesses

6 Citations

Explore all metrics

A systematic and organized overview of various existing transportation problems and their extensions developed by different researchers is offered in the review article. The article has gone through different research papers and books available in Google scholar, Sciencedirect, Z-library Asia, Springer.com, Research-gate, shodhganga, and many other E-learning platforms. The main purpose of the review paper is to recapitulate the existing form of various types of transportation problems and their systematic developments for the guidance of future researchers to help them classify the varieties of problems to be solved and select the criteria to be optimized.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Last-mile delivery concepts: a survey from an operational research perspective

Vehicle routing problem and related algorithms for logistics distribution: a literature review and classification

Public transportation and sustainability: A review

Data availability.

No data is used to prepare this article.

Monge, G.: The founding fathers of optimal transport. Springer, Cham (1781)

Google Scholar  

Tolstoĭ, A.: On the history of the transportation and maximum flow problems. Math. Program. 91 , 437–445 (1930)

MathSciNet   Google Scholar  

Kantorovich, L.V.: Mathematical methods of organizing and planning production. Manag. Sci. 6 (4), 366–422 (1960). https://doi.org/10.1287/mnsc.6.4.366

Article   MathSciNet   MATH   Google Scholar  

Hitchcock, F.L.: The distribution of a product from several sources to numerous localities. J. Math. Phys. 20 (1–4), 224–230 (1941). https://doi.org/10.1002/sapm1941201224

Koopmans, T.: A model of transportation. Act. Anal. Prod. Alloc. (1951). http://web.eecs.umich.edu/~pettie/matching/Koopmans-Reiter-mincost-flow-model-Cowlescommision-report.pdf . Accessed 12 Oct 2020

Charnes, A., Cooper, W.W.: The stepping stone method of explaining linear programming calculations in transportation problems. Manag. Sci. 1 (1), 49–69 (1954). https://doi.org/10.1287/mnsc.1.1.49

Dantzig, G.: Application of the simplex method to a transportation problem. Act. Anal. Prod. Alloc. (1951). https://ci.nii.ac.jp/naid/10021311930/ . Accessed 12 Oct 2020

Hitchcock, F.: The distribution of a product from several sources to numerous localities. Int. J. Pharm. Technol. 8 (1), 3554–3570 (2016)

Sungeeta, S., Renu, T., Deepali, S.: A review on fuzzy and stochastic extensions of the Multi Index transportation problem. Yugoslav. J. Oper. Res. 27 (1), 3–29 (2017)

Gupta, R., Komal.: Literature Survey on Single and Multi-Objective Transportation Problems. Proceedings of International Conference on Sustainable Computing in Science, Technology and Management (SUSCOM), Amity University Rajasthan, Jaipur - India (2019)

Klein, M.: A primal method for minimal cost flows with applications to the assignment and transportation problems. Manag. Sci. 14 (3), 205–220 (1967). https://doi.org/10.1287/mnsc.14.3.205

Article   MATH   Google Scholar  

Lee, S.M., Moore, L.J.: Optimizing transportation problems with multiple objectives. AIIE Trans. 5 (4), 333–338 (1973). https://doi.org/10.1080/05695557308974920

Article   Google Scholar  

Kwak, N., Schniederjans, M.J.: A goal programming model for improved transportation problem solutions. Omega 7 , 367–370 (1979). https://www.sciencedirect.com/science/article/pii/0305048379900458 . Accessed 12 Oct 2020

Ahuja, R.K.: Algorithms for the minimax transportation problem. Nav. Res. Logist. Q. 33 (4), 725–739 (1986). https://doi.org/10.1002/nav.3800330415

Currin, D.C.: Transportation problems with inadmissible routes. J. Oper. Res. Soc. 37 (4), 387–396 (1986). https://doi.org/10.1057/jors.1986.66

Shafaat, A., Goyal, S.K.: Resolution of degeneracy in transportation problems. J. Oper. Res. Soc. 39 (4), 411–413 (1988). https://doi.org/10.1057/jors.1988.69

Arsham, H., Kahn, A.B.: A simplex-type algorithm for general transportation problems: an alternative to stepping-stone. J. Oper. Res. Soc. 40 (6), 581–590 (1989). https://doi.org/10.1057/jors.1989.95

Kirca, Ö., Şatir, A.: A heuristic for obtaining an initial solution for the transportation problem. J. Oper. Res. Soc. 41 (9), 865–871 (1990). https://doi.org/10.1057/jors.1990.124

Goczyłla, K., Cielatkowski, J.: Optimal routing in a transportation network. Eur. J. Oper. Res. 87 , 214–222 (1995)

Adlakha, V., Kowalski, K.: An alternative solution algorithm for certain transportation problems. Int. J. Math. Educ. Sci. Technol. 30 (5), 719–728 (2010). https://doi.org/10.1080/002073999287716

Minghe, S.: The transportation problem with exclusionary side constraints and two branch-and-bound algorithms. Eur. J. Oper. Res. 140 , 629–647 (2002)

Sharma, R., Gaur, A., Okunbor, D.: Management decision-making for transportation problems through goal programming. J. Acad. Bus. Econ. 4 , 195 (2004)

Imam, T., Elsharawy, G., Gomah, M., Samy, I.: Solving transportation problem using object-oriented model. IJCSNS 9 , 353 (2009)

Adlakha, V.: Alternate solutions analysis for transportation problems (2009). https://clutejournals.com/index.php/JBER/article/view/2354 . Accessed 12 Oct 2020

Pandian, P., Natarajan, G.: A new method for finding an optimal solution for transportation problems. Int. J. Math. Sci. Eng. Appl. 4 , 59–65 (2010)

MathSciNet   MATH   Google Scholar  

Korukoğlu, S., Ballı, S.: An improved Vogel’s approximation method for the transportation problem. Math. Comput. Appl. 16 , 370–381 (2011)

Sharma, G., Abbas, S., Gupta, V.: Solving transportation problem with the various method of a linear programming problem. Asian J. Curr. Eng. Maths 1 , 81–83 (2012)

Sharma, G., Abbas, S., Gupta, V.K.: Solving transportation problem with the help of integer programming problem. IOSR J. Eng. 2 , 1274–1277 (2012)

Joshi, R.V.: Optimization techniques for transportation problems of three variables. IOSR J. Math. 9 , 46–50 (2013)

Rekha, S., Srividhya, B., Vidya, S.: Transportation cost minimization: max–min penalty approach. IOSR J. Math. 10 , 6–8 (2014)

Azad, S., Hossain, M., Rahman, M.: An algorithmic approach to solve transportation problems with the average total opportunity cost method. Int. J. Sci. Res. Publ. 7 , 262–270 (2017)

Singh, S.: Note on transportation problem with a new method for the resolution of degeneracy. Univers. J. Ind. Bus. Manag. 3 , 26–36 (2015)

Palanievel, M., Suganya, M.: A new method to solve transportation problem-Harmonic Mean approach. Eng. Technol. Open Access J. 2 , 1–3 (2018)

Charnes, A., Klingman, D.: The more-for-less paradox in the distribution model. Cahiers du Centre d’Etudes de Recherche Operationelle 13 , 11–22 (1971)

Klingman, D., Russell, R.: The transportation problem with mixed constraints. J. Oper. Res. Soc. 25 (3), 447–455 (1974). https://doi.org/10.1057/jors.1974.78

Robb, D.J.: The ‘more for less’ paradox in distribution models: an intuitive explanation. IIE Trans. 22 (4), 377–378 (2007). https://doi.org/10.1080/07408179008964192

Article   MathSciNet   Google Scholar  

Arora, S., Ahuja, A.: A paradox in a fixed charge transportation problem. Indian J. Pure Appl. Math. 31 , 809–822 (2000)

Adlakha, V., Kowalski, K.: A heuristic method for ‘more-for-less’ in distribution-related problems. Int. J. Math. Educ. Sci. Technol. 32 (1), 61–71 (2001). https://doi.org/10.1080/00207390117225

Adlakha, V., Kowalski, K., Lev, B.: Solving transportation problems with mixed constraints. Int. J. Manag. Sci. Eng. Manag. 1 (1), 47–52 (2006). https://doi.org/10.1080/17509653.2006.10670996

Storøy, S.: The transportation paradox revisited (2007). http://web.ist.utl.pt/mcasquilho/compute/_linpro/2007Storoy.pdf . Accessed 13 Oct 2020

Pandian, P., Natarajan, G.: Fourier methods for solving transportation problems with mixed constraints. Int. J. Contemp. Math. Sci. 5 , 1385–1395 (2010)

Joshi, V., Gupta, N.: Linear fractional transportation problem with varying demand and supply Vishwas Deep Joshi–Nilama Gupta. Matematiche (Catania) (2011). https://doi.org/10.4418/2011.66.2.1

Joshi, V.D., Gupta, N.: Identifying more-for-less paradox in the linear fractional transportation problem using objective matrix (2012). https://matematika.utm.my/index.php/matematika/article/view/572 . Accessed 13 Oct 2020

Pandian, P., Anuradha, D.: Path method for finding a more-for-less optimal solution to transportation problems. In: International Conference on Mathematical Computer Engineering (2013)

George, A.O., Jude, O., Anderson, C.N.: Paradox algorithm in application of a linear transportation problem. Am. J. Appl. Math. Stat. 2 , 10–15 (2014)

Gupta, S., Ali, I., Ahmed, A.: Multi-choice multi-objective capacitated transportation problem: a case study of uncertain demand and supply. J. Stat. Manag. Syst. 21 (3), 467–491 (2018). https://doi.org/10.1080/09720510.2018.1437943

Agarwal, S., Sharma, S.: A shootout method for time minimizing transportation problem with mixed constraints. Am. J. Math. Manag. Sci. 39 (4), 299–314 (2020). https://doi.org/10.1080/01966324.2020.1730274

Hammer, P.L.: Time-minimizing transportation problems. Nav. Res. Logist. Q. 16 (3), 345–357 (1969). https://doi.org/10.1002/nav.3800160307

Garfinkel, R.S., Rao, M.R.: The bottleneck transportation problem. Nav. Res. Logist. Q. 18 (4), 465–472 (1971). https://doi.org/10.1002/nav.3800180404

Szwarc, W.: Some remarks on the time transportation problem. Nav. Res. Logist. Q. 18 (4), 473–485 (1971). https://doi.org/10.1002/nav.3800180405

Sharma, J., Swarup, K.: Time minimizing transportation problems. In: Proceedings of the Indian Academy of Sciences (1977)

Varadarajan, R.: An optimal algorithm for 2× n bottleneck transportation problem. Oper. Res. Lett. 10 , 525–529 (1991)

Geetha, S., Nair, K.P.: A stochastic bottleneck transportation problem. J. Oper. Res. Soc. 45 (5), 583–588 (1994). https://doi.org/10.1057/jors.1994.86

Nikolić, I.: Total time minimizing transportation problem. Yugosl. J. Oper. Res. 17 , 125–133 (2007). https://doi.org/10.2298/YUJOR0701125N

Pandian, P., Natarajan, G.: A new method for solving bottleneck-cost transportation problems. In: International Mathematical Forum (2011)

Jain, M., Saksena, P.K.: Time minimizing transportation problem with fractional bottleneck objective function. Yugosl. J. Oper. Res. 22 , 115–129 (2012). https://doi.org/10.2298/YJOR100818004J

Kolman, P.: Time minimizing transportation problems with partial limitations of transported amount for transport participants. In: AIP Conference Proceedings, vol. 1648 (2015). https://doi.org/10.1063/1.4912945

Waldherr, S., Poppenborg, J., Knust, S.: The bottleneck transportation problem with auxiliary resources. 4OR 13 (3), 279–292 (2015). https://doi.org/10.1007/s10288-015-0284-9

Dhanapal, A., Sobana, V.E., Anuradha, D.: On solving bottleneck bi-criteria fuzzy transportation problems. Int. J. Eng. Technol. 7 , 547–551 (2018)

Vidhya, V., Ganesan, K.: A simple method for the solution of bottleneck-cost transportation problem under fuzzy environment. In: AIP Conference Proceedings, vol. 2277, no. 1, p. 090008 (2020). https://doi.org/10.1063/5.0026105

Agarwal, S., Sharma, S.: A shootout method for time minimizing transportation problem with mixed constraints. Am. J. Math. Manag. Sci. (2020). https://doi.org/10.1080/01966324.2020.1730274

Haley, K.B.: New methods in mathematical programming: the solid transportation problem. Oper. Res. 10 (4), 448–463 (1962). https://doi.org/10.1287/opre.10.4.448

Shell, E.: Distribution of product by several properties. In: Proceedings of the Second Symposium in Linear Programming (1955)

Sharma, J.: Extensions and special cases of transportation problem: a survey (1978). Accessed 03 Dec 2020

Haley, K.B.: The existence of a solution to the multi-index problem. J. Oper. Res. Soc. 16 (4), 471–474 (1965). https://doi.org/10.1057/jors.1965.81

Morávek, J., Vlach, M.: Letter to the Editor—On the necessary conditions for the existence of the solution of the multi-index transportation problem. Oper. Res. 15 (3), 542–545 (1967). https://doi.org/10.1287/opre.15.3.542

Smith, G.: A procedure for determining necessary and sufficient conditions for the existence of a solution to the multi-index problem. Aplikace matematiky 19 (3), 177–183 (1974)

Vlach, M.: Conditions for the existence of solutions of the three-dimensional planar transportation problem. Discrete Appl. Math. 13 , 61–78 (1986)

Junginger, W.: On representatives of multi-index transportation problems. Eur. J. Oper. Res. 66 , 353–371 (1993)

Kravtsov, M., Krachkovskii, A.: On some properties of three-index transportation polytopes (1999)

Benterki, D., Zitouni, R., Keraghel, A., Benterki, D.: Elaboration and implantation of an algorithm solving a capacitated four-index transportation. Appl. Math. Sci. 1 , 2643–2657 (2007). https://www.researchgate.net/publication/267118025 . Accessed 14 Oct 2020

Dhanapal, A., Pandian, P., Anuradha, D.: A new approach for solving solid transportation problems. Appl. Math. Sci. 4 , 3603–3610 (2010)

Pham, T., Dott, P.: Four indexes transportation problem with interval cost parameter for goods allocation planning. In: 2012 4th IEEE International Symposium on Logistics and Industrial Informatics (2012)

Halder, S., Das, B., Panigrahi, G., Maiti, M.: Solving a solid transportation problem through fuzzy ranking. In: Lecture Notes Electrical Engineering, vol. 470, pp. 283–292 (2017). https://doi.org/10.1007/978-981-10-8585-7_27

Bandopadhyaya, L., Puri, M.C.: Impaired flow multi-index transportation problem with axial constraints. J. Aust. Math. Soc. Ser. B 29 , 296–309 (2018). https://doi.org/10.1017/S0334270000005828

Halder Jana, S., Giri, D., Das, B., Panigrahi, G., Jana, B., Maiti, M.: A solid transportation problem with additional constraints using Gaussian type-2 fuzzy environments. In: Springer Proceedings in Mathematics and Statistics, vol. 253, pp. 113–125. Springer, New York (2018)

Das, A., Bera, U.K., Maiti, M.: A solid transportation problem in an uncertain environment involving a type-2 fuzzy variable. Neural Comput. Appl. 31 (9), 4903–4927 (2019). https://doi.org/10.1007/s00521-018-03988-8

Hirsch, W.M., Dantzig, G.B.: The fixed charge problem. Nav. Res. Logist. Q. 15 (3), 413–424 (1968). https://doi.org/10.1002/nav.3800150306

Balinski, M.L.: Fixed-cost transportation problems. Nav. Res. Logist. Q. 8 (1), 41–54 (1961). https://doi.org/10.1002/nav.3800080104

Kowalski, K., Lev, B.: On step fixed-charge transportation problem. Omega 36 , 913–917 (2008)

Kuhn, H.W., Baumol, W.J.: An approximative algorithm for the fixed-charges transportation problem. Nav. Res. Logist. Q. 9 (1), 1–15 (1962). https://doi.org/10.1002/nav.3800090102

Robers, P., Cooper, L.: A study of the fixed charge transportation problem. Comput. Math. Appl. 2 , 125–135 (1976)

Diaby, M.: Successive linear approximation procedure for generalized fixed-charge transportation problems. J. Oper. Res. Soc. 42 (11), 991–1001 (1991). https://doi.org/10.1057/jors.1991.189

Kennington, J., Unger, E.: New branch-and-bound algorithm for the fixed-charge transportation problem. Manag. Sci. 22 (10), 1116–1126 (1976). https://doi.org/10.1287/mnsc.22.10.1116

Gray, P.: Technical note-exact solution of the fixed-charge transportation problem. Oper. Res. 19 (6), 1529 (1971). https://doi.org/10.1287/opre.19.6.1529

Sandrock, K.: A simple algorithm for solving small, fixed-charge transportation problems. J. Oper. Res. Soc. 39 (5), 467–475 (1988)

Palekar, U.S., Karwan, M.H., Zionts, S.: A branch-and-bound method for the fixed charge transportation problem. Manag. Sci. 36 (9), 1092–1105 (1990). https://doi.org/10.1287/mnsc.36.9.1092

Diaby, M.: Successive linear approximation procedure for generalized fixed-charge transportation problems. J. Oper. Res. Soc. 42 , 991–1001 (1991)

Hultberg, T., Cardoso, D.: The teacher assignment problem: a special case of the fixed charge transportation problem. Eur. J. Oper. Res. 101 , 463–473 (1997)

Adlakha, V., Kowalski, K.: On the fixed-charge transportation problem. Omega 27 (3), 381–388 (1999). https://doi.org/10.1016/S0305-0483(98)00064-4

Raj, K.A.A.D., Rajendran, C.: A hybrid genetic algorithm for solving single-stage fixed-charge transportation problems. Technol. Oper. Manag. 2 (1), 1–15 (2011). https://doi.org/10.1007/s13727-012-0001-2

Altassan, K.M., Moustafa El-Sherbiny, M., Sasidhar, B., El-Sherbiny, M.M.: Near-Optimal Solution For The Step Fixed Charge Transportation Problem. Appl. Math. Inf. Sci. 7 (2), 661–669 (2013). https://doi.org/10.12785/amis/072L41

Molla-Alizadeh-Zavardehi, S., et al.: Step fixed charge transportation problems via the genetic algorithm. Indian J. Sci. Technol. 7 , 949 (2014)

Sagratella, S., Schmidt, M., Sudermann-Merx, N.: The noncooperative fixed charge transportation problem. Eur. J. Oper. Res. 284 (1), 373–382 (2020). https://doi.org/10.1016/j.ejor.2019.12.024

Roy, S.K., Midya, S., Weber, G.W.: Multi-objective multi-item fixed-charge solid transportation problem under twofold uncertainty. Neural Comput. Appl. 31 (12), 8593–8613 (2019). https://doi.org/10.1007/s00521-019-04431-2

Biswas, A., Shaikh, A.A., Niaki, S.T.A.: Multi-objective non-linear fixed charge transportation problem with multiple modes of transportation in crisp and interval environments. Appl. Soft Comput. J. 80 , 628–649 (2019). https://doi.org/10.1016/j.asoc.2019.04.011

Midya, S., Roy, S.K.: Multi-objective fixed-charge transportation problem using rough programming. Int. J. Oper. Res. 37 (3), 377–395 (2020). https://doi.org/10.1504/IJOR.2020.105444

Singh, G., Singh, A.: Solving multi-objective fixed charged transportation problem using a modified particle swarm optimization algorithm. In: Lecture Notes on Data Engineering and Communications Technologies, vol. 53, pp. 373–386. Springer (2021)

Mahapatra, D.R.: Multi-choice stochastic transportation problem involving Weibull distribution. Int. Optim. Control Theor. Appl. 4 (1), 45–55 (2013). https://doi.org/10.11121/ijocta.01.2014.00154

Maity, G., Roy, S.K.: Solving multi-choice multi-objective transportation problem: a utility function approach. J. Uncertain. Anal. Appl. (2014). https://doi.org/10.1186/2195-5468-2-11

Quddoos, A., ull Hasan, M.G., Khalid, M.M.: Multi-choice stochastic transportation problem involving a general form of distributions. J. Korean Phys. Soc. 3 (1), 1–9 (2014). https://doi.org/10.1186/2193-1801-3-565

Roy, S.K.: Transportation problem with multi-choice cost and demand and stochastic supply. J. Oper. Res. Soc. China 4 (2), 193–204 (2016). https://doi.org/10.1007/s40305-016-0125-3

Ranarahu, N., Dash, J.K., Acharya, S.: Computation of Multi-choice Multi-objective Fuzzy Probabilistic Transportation Problem, pp. 81–95. Springer, Singapore (2019)

Agrawal, P., Ganesh, T.: Multi-choice stochastic transportation problem involving logistic distribution. Adv. Appl. Math. Sci. 18 , 45–58 (2018)

Al Qahtani, H., El-Hefnawy, A., El-Ashram, M.M., Fayomi, A.: A goal programming approach to multichoice multiobjective stochastic transportation problems with extreme value distribution. Adv. Oper. Res. (2019). https://doi.org/10.1155/2019/9714137

Nayak, J., et al.: Generalized binary variable approach to solving Multi-Choice transportation problem-Indian Journals. https://www.indianjournals.com/ijor.aspx?target=ijor:ijesm&volume=6&issue=5&article=012 . Accessed 27 Jan 2021

Agrawal, P., Ganesh, T.: Solution of stochastic transportation problem involving multi-choice random parameter using Newton’s divided difference interpolation. J. Inf. Optim. Sci. (2020). https://doi.org/10.1080/02522667.2019.1694741

Chanas, S., Delgado, M., Verdegay, J.L., Vila, M.A.: Interval and fuzzy extensions of classical transportation problems. Transp. Plan. Technol. 17 (2), 203–218 (1993). https://doi.org/10.1080/03081069308717511

Baidya, A., Bera, U.K., Maiti, M.: Multi-item interval-valued solid transportation problem with safety measure under fuzzy-stochastic environment. J. Transp. Secur. 6 (2), 151–174 (2013). https://doi.org/10.1007/s12198-013-0109-z

Rani, D., Gulati, T.R.: Fuzzy optimal solution of interval-valued fuzzy transportation problems. Adv. Intell. Syst. Comput. 258 , 881–888 (2014). https://doi.org/10.1007/978-81-322-1771-8_76

Yu, V.F., Hu, K.J., Chang, A.Y.: An interactive approach for the multi-objective transportation problem with interval parameters. Int. J. Prod. Res. 53 (4), 1051–1064 (2015). https://doi.org/10.1080/00207543.2014.939236

Ebrahimnejad, A.: Fuzzy linear programming approach for solving transportation problems with interval-valued trapezoidal fuzzy numbers. Sadhana Acad. Proc. Eng. Sci. 41 (3), 299–316 (2016). https://doi.org/10.1007/s12046-016-0464-0

Henriques, C.O., Coelho, D.: Multiobjective Interval Transportation Problems: A Short Review, pp. 99–116. Springer, Cham (2017)

Akilbasha, A., Pandian, P., Natarajan, G.: An innovative exact method for solving fully interval integer transportation problems. Inform. Med. Unlocked 11 , 95–99 (2018). https://doi.org/10.1016/j.imu.2018.04.007

Ramesh, G., Sudha, G., Ganesan, K.: A novel approach for the solution of multi-objective interval transportation problem. In: Journal of Physics: Conference Series, vol. 1000, no. 1 (2018). https://doi.org/10.1088/1742-6596/1000/1/012010

Malik, M., Gupta, S.K.: Goal programming technique for solving fully interval-valued intuitionistic fuzzy multiple objective transportation problems. Soft Comput. 24 (18), 13955–13977 (2020). https://doi.org/10.1007/s00500-020-04770-6

Bharati, S.K.: Transportation problem with interval-valued intuitionistic fuzzy sets: impact of a new ranking. Prog. Artif. Intell. (2021). https://doi.org/10.1007/s13748-020-00228-w

Chanas, S., Kołodziejczyk, W., Machaj, A.: A fuzzy approach to the transportation problem. Fuzzy Sects Syst. 13 , 211–221 (1984)

Chanas, S., Kuchta, D.: A concept of the optimal solution of the transportation problem with fuzzy cost coefficients. Fuzzy Sets Syst. 82 (3), 299–305 (1996). https://doi.org/10.1016/0165-0114(95)00278-2

Tada, M., Ishii, H.: An integer fuzzy transportation problem. Comput. Math. Appl. 31 , 71–87 (1996)

Liu, S., Kao, C.: Solving fuzzy transportation problems based on extension principle. Eur. J. Oper. Res. 153 , 661–674 (2004)

Gani, A.N., Razak, K.A.: Two-stage fuzzy transportation problem (2006). Accessed 14 Oct 2020

Gupta, P., Mehlawat, M.: An algorithm for a fuzzy transportation problem to select a new type of coal for a steel manufacturing unit. TOP 15 , 114–137 (2007). https://link.springer.com/content/pdf/10.1007/s11750-007-0006-3.pdf . Accessed 14 Oct 2020

Li, L., Huang, Z., Da, Q., Hu, J.: A new method based on goal programming for solving transportation problem with fuzzy cost. In: Proceedings—International Symposium on Information Processing, ISIP 2008 and International Pacific Workshop on Web Mining and Web-Based Application, WMWA 2008, pp. 3–8 (2008). https://doi.org/10.1109/ISIP.2008.9

Lin, F.: Solving the transportation problem with fuzzy coefficients using genetic algorithms. In: 2009 IEEE International Conference on Fuzzy Systems (2009)

Pandian, P., Natarajan, G.: A new algorithm for finding an optimal fuzzy solution for fuzzy transportation problems. Appl. Math. Sci. 4 , 79–90 (2010)

MATH   Google Scholar  

Güzel, N.: Fuzzy transportation problem with the fuzzy amounts and the fuzzy costs. World Appl. Sci. J. 8 (5), 543–549 (2010)

Kumar, A., Kaur, A.: Application of classical transportation methods to find the fuzzy optimal solution of fuzzy transportation problems. Fuzzy Inf. Eng 1 (1), 81–99 (2011). https://doi.org/10.1007/s12543-011-0068-7

Gani, A.N., Samuel, A.E., Anuradha, D.: Simplex type algorithm for solving fuzzy transportation problem. Tamsui Oxf. J. Inf. Math. Sci. 27 (1), 89–98 (2011). https://doi.org/10.13140/2.1.1865.7929

Kumar, B., Murugesan, S.: On fuzzy transportation problem using triangular fuzzy numbers with the modified, revised simplex method. Int. J. Eng. Sci. Technol. 4 (2012), 285–294 (2012)

Ebrahimnejad, A.: A simplified new approach for solving fuzzy transportation problems with generalized trapezoidal fuzzy numbers. Appl. Soft. Comput. 19 , 171–176 (2014)

Das, U.K., Ashraful-Babu, R., Khan, A., Helal, U.: Logical development of Vogel’s approximation method (LD-VAM): an approach to find basic feasible solution of transportation problem. Int. J. Sci. Technol. Res. 3 (2), 42–48 (2014)

Elmaghraby, S.E.: Allocation under uncertainty when the demand has continuous D.F. Manag. Sci. 6 (3), 270–294 (1960). https://doi.org/10.1287/mnsc.6.3.270

Williams, A.C.: A stochastic transportation problem. Oper. Res. 11 (5), 759–770 (1963). https://doi.org/10.1287/opre.11.5.759

Szwarc, W.: The transportation problem with stochastic demand. Manag. Sci. 11 (1), 33–50 (1964). https://doi.org/10.1287/mnsc.11.1.33

Wilson, D.: An a priori bounded model for transportation problems with stochastic demand and integer solutions. AIIE Trans. 4 (3), 186–193 (1972). https://doi.org/10.1080/05695557208974848

Cooper, L., Leblanc, L.J.: Stochastic transportation problems and other network-related convex problems. Nav. Res. Logist. Q. 24 (2), 327–337 (1977). https://doi.org/10.1002/nav.3800240211

LeBlanc, L.J.: A heuristic approach for large scale discrete stochastic transportation-location problems. Comput. Math. Appl. 3 , 87–94 (1977)

Holmberg, K., Joernsten, K.: Cross decomposition applied to the stochastic transportation problem. Eur. J. Oper. Res. 17 (1984), 361–368 (1984)

Qi, L.: Forest iteration method for stochastic transportation problem. Math. Program. Study 25 , 142–163 (1985). https://doi.org/10.1007/bfb0121081

Freling, R., Romeijn, H.E., Morales, D.R., Wagelmans, A.P.M.: A branch-and-price algorithm for the multiperiod single-sourcing problem. Oper. Res. 51 (6), 922–939 (2003). https://doi.org/10.1287/opre.51.6.922.24914

Larsson, T., Patriksson, M., Rydergren, C., Daneva, M.: A comparison of feasible direction methods for the stochastic transportation problem. Comput. Optim. Appl. 46 (3), 451–466 (2008). https://doi.org/10.1007/s10589-008-9199-0

Mahapatra, D.R., Roy, S.K., Biswal, M.P.: Stochastic based on multi-objective transportation problems involving normal randomness. Adv. Model. Optim. 12 (2), 205–223 (2010)

Ge, Y., Ishii, H.: Stochastic bottleneck transportation problem with flexible supply and demand quantity. Kybernetika 47 , 560–571 (2011)

Akdemir, H.G., Tiryaki, F., Günay Akdemir, H.: Bilevel stochastic transportation problem with exponentially distributed demand. Bitlis Eren Univ. J. Sci. Technol. (2012). https://doi.org/10.17678/beuscitech.47150

Biswal, M.P., Samal, H.K.: Stochastic transportation problem with cauchy random variables and multi choice parameters (2013). Accessed 15 Oct 2020

Hinojosa, Y., Puerto, J., Saldanha-da-Gama, F.: A two-stage stochastic transportation problem with fixed handling costs and a priori selection of the distribution channels. TOP 22 , 1123–1147 (2014). https://link.springer.com/content/pdf/10.1007/s11750-014-0321-4.pdf . Accessed 15 Oct 2020

Stewart, T.J., Ittmann, H.W.: Two-stage optimization in a transportation problem. J. Oper. Res. Soc. 30 (10), 897–904 (1979). https://doi.org/10.1057/jors.1979.210

Fulya, M.G., Lin, A.L., Gen, M., Lin, L., Altiparmak, F.: A genetic algorithm for two-stage transportation problem using priority-based encoding. OR Spectr. (2006). https://doi.org/10.1007/s00291-005-0029-9

Tang, L., Gong, H.: A hybrid two-stage transportation and batch scheduling problem. Appl. Math. Model. 32 (12), 2467–2479 (2008). https://doi.org/10.1016/j.apm.2007.09.028

Sudhakar, V.J., Kumar, V.N.: Solving the multiobjective two-stage fuzzy transportation problem by zero suffix method (2010). [Online]. Available: www.ccsenet.org/jmr . Accessed 22 Feb 2021

Pandian, P., Natarajan, G.: Solving two-stage transportation problems. In: Communications in Computer and Information Science, 2011, vol. 140, CCIS, pp. 159–165 (2011). https://doi.org/10.1007/978-3-642-19263-0_20

Raj, K.A.A.D., Rajendran, C.: A genetic algorithm for solving the fixed-charge transportation model: two-stage problem. Comput. Oper. Res. 39 (9), 2016–2032 (2012). https://doi.org/10.1016/j.cor.2011.09.020

Calvete, H.I., Galé, C., Iranzo, J.A.: An improved evolutionary algorithm for the two-stage transportation problem with the fixed charge at depots. OR Spectr. 38 (1), 189–206 (2016). https://doi.org/10.1007/s00291-015-0416-9

Roy, S.K., Maity, G., Weber, G.W.: Multi-objective two-stage grey transportation problem using utility function with goals. Cent. Eur. J. Oper. Res. 25 (2), 417–439 (2017). https://doi.org/10.1007/s10100-016-0464-5

Malhotra, R.: A polynomial algorithm for a two-stage time minimizing transportation problem. Opsearch 39 (5–6), 251–266 (2002). https://doi.org/10.1007/bf03399188

Cosma, O., Pop, P.C., Sabo, C.: A novel hybrid genetic algorithm for the two-stage transportation problem with fixed charges associated to the routes. In: Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Jan 2020, vol. 12011, LNCS, pp. 417–428 (2020). https://doi.org/10.1007/978-3-030-38919-2_34

Khanna, S., Puri, M.C.: A paradox in linear fractional transportation problems with mixed constraints. Optimization 27 (4), 375–387 (1993). https://doi.org/10.1080/02331939308843896

Stancu-Minasian, I.M.: Fractional Transportation Problem, pp. 336–364. Springer, Dordrecht (1997)

Joshi, V.D., Gupta, N.: Linear fractional transportation problem with varying demand and supply. Matematiche (Catania) LXVI , 3–12 (2011). https://doi.org/10.4418/2011.66.2.1

Saxena, A., Singh, P., Saxena, P.K.: Quadratic fractional transportation problem with additional impurity restrictions. J. Stat. Manag. Syst. 10 (3), 319–338 (2007). https://doi.org/10.1080/09720510.2007.10701257

Khurana, A., Arora, S.R.: The sum of a linear and a linear fractional transportation problem with the restricted and enhanced flow. J. Interdiscip. Math. 9 (2), 373–383 (2006). https://doi.org/10.1080/09720502.2006.10700450

Liu, S.: Fractional transportation problem with fuzzy parameters. Soft Comput. (2015). https://doi.org/10.1007/s00500-015-1722-5

Mohanaselvi, S., Ganesan, K.: A new approach for solving linear fuzzy fractional transportation problem. Int. J. Civ. Eng. Technol. 8 (8), 1123–1129 (2017)

Anukokila, P., Anju, A., Radhakrishnan, B.: Optimality of intuitionistic fuzzy fractional transportation problem of type-2. Arab J. Basic Appl. Sci. 26 (1), 519–530 (2019). https://doi.org/10.1080/25765299.2019.1691895

Anukokila, P., Radhakrishnan, B.: Goal programming approach to the fully fuzzy fractional transportation problem. J. Taibah Univ. Sci. 13 (1), 864–874 (2019). https://doi.org/10.1080/16583655.2019.1651520

El Sayed, M.A., Abo-Sinna, M.A.: A novel approach for fully intuitionistic fuzzy multi-objective fractional transportation problem. Alex. Eng. J. 60 (1), 1447–1463 (2021). https://doi.org/10.1016/j.aej.2020.10.063

Rubin, P., Narasimhan, R.: Fuzzy goal programming with nested priorities. Fuzzy Sets Syst. 14 , 115–129 (1984)

Charnes, A., Cooper, W.W.: Management models and industrial applications of linear programming. Manag. Sci. 4 (1), 38–91 (1957). https://doi.org/10.1287/mnsc.4.1.38

Zimmermann, H.: Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1 , 45–55 (1978)

Diaz, J., Ja, D.: Finding a complete description of all efficient solutions to a multiobjective transportation problem (1979). Accessed 22 Nov 2020

Isermann, H.: The enumeration of all efficient solutions for a linear multiple-objective transportation problem. Nav. Res. Logist. Q. 26 (1), 123–139 (1979). https://doi.org/10.1002/nav.3800260112

Leberling, H.: On finding compromise solutions in multicriteria problems using the fuzzy min-operator. Fuzzy Sets Syst. 6 , 105–118 (1981)

Majumdar, M., Mitra, T.: Dynamic optimization with a non-convex technology: the case of a linear objective function. Rev. Econ. Stud. 50 , 143–151 (1983)

Słowiński, R.: A multicriteria fuzzy linear programming method for water supply system development planning. Fuzzy Sets Syst. 19 (3), 217–237 (1986). https://doi.org/10.1016/0165-0114(86)90052-7

Ringuest, J., Rinks, D.: Interactive solutions for the linear multiobjective transportation problem. Eur. J. Oper. Res. 32 , 96–106 (1987)

Bit, A., Biswal, M., Alam, S.: Fuzzy programming approach to multicriteria decision making transportation problem. Fuzzy Sets Syst. 50 , 135–141 (1992)

Verma, R., Biswal, M., Biswas, A.: Fuzzy programming technique to solve multi-objective transportation problems with some non-linear membership functions. Fuzzy Sets Syst. 91 , 37–43 (1997)

Gen, M., Li, Y., Gen, M., Ida, K.: Solving multi-objective transportation problem by spanning tree-based genetic algorithm. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 82 , 2802–2810 (2000)

Das, S., Goswami, A., Alam, S.: Multiobjective transportation problem with interval cost, source and destination parameters. Eur. J. oper. Res. 117 , 100–112 (1999)

Li, L., Lai, K.: A fuzzy approach to the multiobjective transportation problem. Comput. Oper. Res. 27 , 43–57 (2000)

Abd El-Wahed, W.: A multi-objective transportation problem under fuzziness Fuzzy Approach. Fuzzy Sets Syst. 117 , 27–33 (2001)

Ammar, E., Youness, E.: Study on multiobjective transportation problem with fuzzy numbers. Appl. Math. Comput. 166 , 241–253 (2005)

Abd El-Wahed, W.F., Lee, S.M.: Interactive fuzzy goal programming for multi-objective transportation problems. Omega 34 , 158–166 (2006). https://doi.org/10.1016/j.omega.2004.08.006

Zangiabadi, M., Maleki, H.R.: Fuzzy goal programming for multiobjective transportation problems. J. Appl. Math. Comput. 24 (1–2), 449–460 (2007). https://doi.org/10.1007/BF02832333

Lau, H.C.W., Chan, T.M., Tsui, W.T., Chan, F.T.S., Ho, G.T.S., Choy, K.L.: A fuzzy guided multi-objective evolutionary algorithm model for solving transportation problem. Expert Syst. Appl. 36 (4), 8255–8268 (2009). https://doi.org/10.1016/j.eswa.2008.10.031

Lohgaonkar, M., Bajaj, V.: Fuzzy approach to solve the multi-objective capacitated transportation problem. Int. J. Bioinform. 2 , 10–14 (2010)

Pal, B.B., Kumar, M., Sen, S.: Priority based fuzzy goal programming approach for fractional multilevel programming problems. Int. Rev. Fuzzy Math. 6 (2), 1–14 (2011)

Zaki, S., Allah, A.A., Geneedi, H., Elmekawy, A.; Efficient multiobjective genetic algorithm for solving transportation, assignment, and transshipment problems (2012). Accessed 22 Nov 2020

Maity, G., Roy, S.K.: Solving a multi-objective transportation problem with nonlinear cost and multi-choice demand. Int. J. Manag. Sci. Eng. Manag. 11 (1), 62–70 (2016). https://doi.org/10.1080/17509653.2014.988768

Roy, S.K., Maity, G., Weber, G.-W.: Multi-objective two-stage grey transportation problem using utility function with goals. Artic. Cent. Eur. J. Oper. Res. (2017). https://doi.org/10.1007/s10100-016-0464-5

Biswas, A., Shaikh, A., Niaki, S.: Multi-objective non-linear fixed charge transportation problem with multiple modes of transportation in crisp and interval environments. Appl. Soft. Comput. 80 , 628–649 (2019)

Bera, R.K., Mondal, S.K.: Analyzing a two-staged multi-objective transportation problem under quantity dependent credit period policy using q-fuzzy number. Int. J. Appl. Comput. Math. (2020). https://doi.org/10.1007/s40819-020-00901-7

Download references

Acknowledgements

First author (Yadvendra Kacher) acknowledges the financial support as Junior research fellowship (JRF) received from CSIR (Govt. of India) through HRDG(CSIR) senction Letter No./File No.: 09/1032(0019)/2019-EMR-I.

Author information

Authors and affiliations.

Department of Mathematics, Motilal Nehru National Institute of Technology Allahabad, Prayagraj, 211004, India

Yadvendra Kacher & Pitam Singh

You can also search for this author in PubMed   Google Scholar

Contributions

Both the authors contributed equally in developing the whole article.

Corresponding author

Correspondence to Pitam Singh .

Ethics declarations

Conflict of interest.

The authors declare that they have no conflicts of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Kacher, Y., Singh, P. A Comprehensive Literature Review on Transportation Problems. Int. J. Appl. Comput. Math 7 , 206 (2021). https://doi.org/10.1007/s40819-021-01134-y

Download citation

Accepted : 26 August 2021

Published : 24 September 2021

DOI : https://doi.org/10.1007/s40819-021-01134-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Transportation problem
• Multi-objective transportation problem
• Optimal solution
• Fuzzy programming
• Goal programming
• Find a journal
• Publish with us
• Track your research

• Open access
• Published: 20 July 2023

Solving a multi-objective solid transportation problem: a comparative study of alternative methods for decision-making

• Mohamed H. Abdelati   ORCID: orcid.org/0000-0002-5034-7323 1 ,
• Ali M. Abd-El-Tawwab 1 ,
• Elsayed Elsayed M. Ellimony 2 &
• M Rabie 1  

Journal of Engineering and Applied Science volume  70 , Article number:  82 ( 2023 ) Cite this article

2345 Accesses

1 Citations

Metrics details

The transportation problem in operations research aims to minimize costs by optimizing the allocation of goods from multiple sources to destinations, considering supply, demand, and transportation constraints. This paper applies the multi-dimensional solid transportation problem approach to a private sector company in Egypt, aiming to determine the ideal allocation of their truck fleet.

In order to provide decision-makers with a comprehensive set of options to reduce fuel consumption costs during transportation or minimize total transportation time, a multi-objective approach is employed. The study explores the best compromise solution by leveraging three multi-objective approaches: the Zimmermann Programming Technique, Global Criteria Method, and Minimum Distance Method. Optimal solutions are derived for time and fuel consumption objectives, offering decision-makers a broad range to make informed decisions for the company and the flexibility to adapt them as needed.

Lingo codes are developed to facilitate the identification of the best compromise solution using different methods. Furthermore, non-dominated extreme points are established based on the weights assigned to the different objectives. This approach expands the potential ranges for enhancing the transfer problem, yielding more comprehensive solutions.

This research contributes to the field by addressing the transportation problem practically and applying a multi-objective approach to support decision-making. The findings provide valuable insights for optimizing the distribution of the truck fleet, reducing fuel consumption costs, and improving overall transportation efficiency.

Introduction

The field of operations research has identified the transportation problem as an optimization issue of significant interest [ 1 , 2 ]. This problem concerns determining the optimal approach to allocate a given set of goods that come from particular sources to the designated destinations to minimize the overall transportation costs [ 3 ]. The transportation problem finds applications in various areas, including logistics planning, distribution network design, and supply chain management. Solving this problem relies on the assumption that the supply and demand of goods are known, as well as the transportation cost for each source–destination pairing [ 4 , 5 ].

Solving the transportation problem means finding the right quantities of goods to be transported from the sources to the destinations, given the supply and demand restrictions. The ultimate goal is to minimize the total transportation cost, which is the sum of the cost for each shipment [ 6 ]. Various optimization algorithms have been developed for this problem, such as the North-West Corner Method, the Least Cost Method, and Vogel’s Approximation Method [ 7 ].

A solid transportation problem (STP) is a related transportation problem that centers around a single commodity, which can be stored at interim points [ 8 ]. These interim points, known as transshipment points, act as origins and destinations. The STP involves determining the most efficient means of transporting the commodity from the sources to the destinations, while minimizing transportation costs by going through the transshipment points. The STP has real-world applications in container shipping, air cargo transportation, and oil and gas pipeline transportation [ 9 , 10 ].

Multi-dimensional solid transportation problem (MDSTP) represents a variation on the STP, incorporating multiple commodities that vary in properties such as volume, weight, and hazard level [ 11 ]. The MDSTP aims to identify the best way to transport each commodity from the sources to the destinations, taking into account the capacity restrictions of transshipment points and hazardous commodity regulations [ 12 ]. The MDSTP is more complex than the STP and requires specific algorithms and models for its resolution.

Solving the STP and MDSTP requires identifying the most effective routing of commodities and considering the storage capacity of transshipment points. The goal is to minimize total transportation costs while satisfying supply and demand constraints and hazardous material regulations. Solutions to these problems include the Network Simplex Method, Branch and Bound Method, and Genetic Algorithm [ 13 ]. Solving the STP and MDSTP contributes valuable insights into the design and operation of transportation systems and supports improved sustainability and efficiency.

In the field of operations research, two critical research areas are the multi-objective transportation problem (MOTP) and the multi-objective solid transportation problem (MOSTP) [ 14 ]. The MOTP aims to optimize the transportation of goods from multiple sources to various destinations by considering multiple objectives, including minimizing cost, transportation time, and environmental impacts. The MOSTP, on the other hand, focuses on the transportation of solid materials, such as minerals or ores, and involves dealing with multiple competing objectives, such as cost, time, and quality of service. These problems are essential in logistics and supply chain management, where decision-makers must make optimal transportation plans by considering multiple objectives. Researchers and practitioners often employ optimization techniques, such as mathematical programming, heuristics, and meta-heuristics, to address these challenges efficiently [ 15 ].

Efficient transportation planning is essential for moving goods from their source to the destination. This process involves booking different types of vehicles and minimizing the total transportation time and cost is a crucial factor to consider. Various challenges can affect the optimal transportation policy, such as the weight and volume of products, the availability of specific vehicles, and other uncertain parameters. In this regard, several studies have proposed different approaches to solve the problem of multi-objective solid transportation under uncertainty. One such study by Kar et al. [ 16 ] used fuzzy parameters to account for uncertain transportation costs and time, and two methods were employed to solve the problem, namely the Zimmermann Method and the Global Criteria Method.

Similarly, Mirmohseni et al. [ 17 ] proposed a fuzzy interactive probabilistic programming approach, while Kakran et al. [ 18 ] addressed a multi-objective capacitated solid transportation problem with uncertain zigzag variables. Additionally, Chen et al. [ 19 ] investigated an uncertain bicriteria solid transportation problem by using uncertainty theory properties to transform the models into deterministic equivalents, proposing two models, namely the expected value goal programming and chance-constrained goal programming models [ 20 ]. These studies have contributed to developing different approaches using fuzzy programming, uncertainty theory, and related concepts to solve multi-objective solid transportation problems with uncertain parameters.

This paper presents a case study carried out on a private sector company in Egypt intending to ascertain the minimum number of trucks required to fulfill the decision-makers’ objectives of transporting the company’s fleet of trucks from multiple sources to various destinations. This objective is complicated by the diversity of truck types and transported products, as well as the decision-makers’ multiple priorities, specifically the cost of fuel consumption and the timeliness of truck arrival.

In contrast to previous research on the transportation problem, this paper introduces a novel approach that combines the multi-dimensional solid transportation problem framework with a multi-objective optimization technique. Building upon previous studies, which often focused on single-objective solutions and overlooked specific constraints, our research critically analyzes the limitations of these approaches. We identify the need for comprehensive solutions that account for the complexities of diverse truck fleets and transported products, as well as the decision-makers’ multiple priorities. By explicitly addressing these shortcomings, our primary goal is to determine the minimum number of trucks required to fulfill the decision-makers’ objectives, while simultaneously optimizing fuel consumption and transportation timeliness. Through this novel approach, we contribute significantly to the field by advancing the understanding of the transportation problem and providing potential applications in various domains. Our research not only offers practical solutions for real-world scenarios but also demonstrates the potential for improving transportation efficiency and cost-effectiveness in other industries or contexts. The following sections will present a comparative analysis of the proposed work, highlighting the advancements and novelty introduced by our approach.

Methods/experimental

This study uses a case study from Egypt to find the optimal distribution of a private sector company’s truck fleet under various optimization and multi-objective conditions. Specifically, the study aims to optimize the distribution of a private sector company’s truck fleet by solving a multi-objective solid transportation problem (MOSTP) and comparing three different methods for decision-making.

Design and setting

This study uses a case study design in a private sector company in Egypt. The study focuses on distributing the company’s truck fleet to transport products from factories to distribution centers.

Participants or materials

The participants in this study are the transportation planners and managers of the private sector company in Egypt. The materials used in this study include data on the truck fleet, sources, destinations, and products.

Processes and methodologies

The study employs the multi-objective multi-dimensional solid transportation problem (MOMDSTP) to determine the optimal solution for the company’s truck fleet distribution, considering two competing objectives: fuel consumption cost and total shipping time. The MOMDSTP considers the number and types of trucks, sources, destinations, and products and considers the supply and demand constraints.

To solve the MOMDSTP, three decision-making methods are employed: Zimmermann Programming Technique, Global Criteria Method, and Minimum Distance Method. The first two methods directly yield the best compromise solution (BCS), whereas the last method generates non-dominated extreme points by assigning different weights to each objective. Lingo software is used to obtain the optimal solutions for fuel consumption cost and time and the BCS and solutions with different weights for both objectives.

Ethics approval and consent

This study does not involve human participants, data, or tissue, nor does it involve animals. Therefore, ethics approval and consent are not applicable.

Statistical analysis

Statistical analysis is not conducted in this study. However, the MOMDSTP model and three well-established decision-making methods are employed to derive the optimal distribution of the company’s truck fleet under various optimization and multi-objective conditions.

In summary, this study uses a case study design to find the optimal distribution of a private sector company’s truck fleet under various optimization and multi-objective conditions. The study employs the MOMDSTP and three methods for decision-making, and data on the truck fleet, sources, destinations, and products are used as materials. Ethics approval and consent are not applicable, and statistical analysis is not performed.

Multi-objective transportation problem

The multi-objective optimization problem is a complex issue that demands diverse approaches to determine the most satisfactory solution. Prevalent techniques employed in this domain include the Weighted Sum Method, Minimum Distance Method, Zimmermann Programming Technique, and Global Criteria Method. Each method offers its own benefits and limitations, and the selection of a specific method depends on the nature of the problem and the preferences of the decision-makers [ 21 ].

This section discusses various methodologies employed to identify the most optimal solution(s) for the multi-objective multi-dimensional solid transportation problem (MOMDSTP), which is utilized as the basis for the case study. These methodologies encompass the Minimum Distance Method (MDM), the Zimmermann Programming Technique, and the Global Criteria Method [ 22 ].

Zimmermann Programming Technique

The Zimmermann Programming Technique (ZPT) is a multi-objective optimization approach that was developed by Professor Hans-Joachim Zimmermann in the late 1970s. This technique addresses complex problems with multiple competing objectives that cannot be optimized simultaneously. Additionally, it incorporates the concept of an “aspiration level,” representing the minimum acceptable level for each objective. The aspiration level ensures that the solution obtained is satisfactory for each objective. If the solution does not meet the aspiration level for any objective, the weights are adjusted, and the optimization process is iterated until a satisfactory solution is obtained.

A key advantage of ZPT is its ability to incorporate decision-makers’ preferences and judgments into the decision-making process. The weights assigned to each objective are based on the decision-maker’s preferences, and the aspiration levels reflect their judgments about what constitutes an acceptable level for each objective [ 23 ].

The Zimmermann Programming Technique empowers decision-makers to incorporate multiple objectives and achieve a balanced solution. By assigning weights to objectives, a trade-off can be made to find a compromise that meets various criteria. For example, this technique can optimize cost, delivery time, and customer satisfaction in supply chain management [ 24 ]. However, the interpretation of results may require careful consideration, and computational intensity can increase with larger-scale and complex problems.

 In order to obtain the solution, each objective is considered at a time to get the lower and upper bounds for that objective. Let for objective, and are the lower (min) and upper (max) bounds. The membership functions of the first and second objective functions can be generated based on the following formula [ 25 ]:

Next, the fuzzy linear programming problem is formulated using the max–min operator as follows:

Maximize min \({\mu }_{k}\left({F}_{k}\left(x\right)\right)\)   

Subject to \({g}_{i}\left(x\right) \left\{ \le ,= , \ge \right\}{b}_{i}\mathrm{ where }\;i = 1, 2, 3, ..., m.\)   

Moreover, x ≥ 0.

Global Criteria Method

The Global Criteria Method is a multi-objective optimization method that aims to identify the set of ideal solutions based on predetermined criteria. This method involves defining a set of decision rules that assess the feasibility and optimality of the solutions based on the objectives and constraints [ 26 ]. By applying decision rules, solutions that fail to meet the predetermined criteria are eliminated, and the remaining solutions are ranked [ 27 ].

The Global Criteria Method assesses overall system performance, aiding decision-makers in selecting solutions that excel in all objectives. However, it may face challenges when dealing with conflicting objectives [ 28 ]. Furthermore, it has the potential to overlook specific details, and the choice of aggregation function or criteria can impact the results by favoring specific solutions or objectives.

Let us consider the following ideal solutions:

f 1* represents the ideal solution for the first objective function,

f 2* represents the ideal solution for the second objective function, and

n 1* represents the ideal solution for the nth objective function.

Objective function formula:

Minimize the objective function F  =  \(\sum_{k=1}^{n}{(\frac{{f}_{k}\left({x}^{*}\right)-{f}_{k}(x)}{{f}_{k}({x}^{*})})}^{p}\)

Subject to the constraints: g i ( x ) \(\le\) 0, i  = 1, 2,.., m

The function fk( x ) can depend on variables x 1 , x 2 , …, x n .

Minimum Distance Method

The Minimum Distance Method (MDM) is a novel distance-based model that utilizes the goal programming weighted method. The model aims to minimize the distances between the ideal objectives and the feasible objective space, leading to an optimal compromise solution for the multi-objective linear programming problem (MOLPP) [ 29 ]. To solve MOLPP, the proposed model breaks it down into a series of single objective subproblems, with the objectives transformed into constraints. To further enhance the compromise solution, priorities can be defined using weights, and a criterion is provided to determine the best compromise solution. A significant advantage of this approach is its ability to obtain a compromise solution without any specific preference or for various preferences.

The Minimum Distance Method prioritizes solutions that closely resemble the ideal or utopian solution, assisting decision-makers in ranking and identifying high-performing solutions. It relies on a known and achievable ideal solution, and its sensitivity to the chosen reference point can influence results. However, it does not provide a comprehensive trade-off solution, focusing solely on proximity to the ideal point [ 30 ].

The mathematical formulation for MDM for MOLP is as follows:

The formulation for multi-objective linear programming (MOLP) based on the minimum distance method is referred to[ 31 ]. It is possible to derive the multi-objective transportation problem with two objective functions using this method and its corresponding formula.

Subject to the following constraints:

f * 1 , f * 2 : the obtained ideal objective values by solving single objective STP.

w 1 , w 2 : weights for objective1 and objective2 respectively.

f 1, f 2: the objective values for another efficient solution.

d : general deviational variable for all objectives.

\({{c}_{ij}^{1}, c}_{ij}^{2}\) : the unit cost for objectives 1 and 2 from source i to destination j .

\({{x}_{ij}^{1}, x}_{ij}^{2}\) : the amount to be shipped when optimizing for objectives 1 and 2 from source i to destination j .

Mathematical model for STP

The transportation problem (TP) involves finding the best method to ship a specific product from a defined set of sources to a designated set of destinations, while adhering to specific constraints. In this case, the objective function and constraint sets take into account three-dimensional characteristics instead of solely focusing on the source and destination [ 32 ]. Specifically, the TP considers various modes of transportation, such as ships, freight trains, cargo aircraft, and trucks, which can be used to represent the problem in three dimensions When considering a single mode of transportation, the TP transforms into a solid transportation problem (STP), which can be mathematically formulated as follows:

The mathematical form of the solid transportation problem is given by [ 33 ]:

Subject to:

Z = the objective function to be minimized

m = the number of sources in the STP

n = the number of destinations in the STP

p = the number of different modes of transportation in the STP

x ijk represents the quantity of product transported from source i to destination j using conveyance k

c ijk = the unit transportation cost for each mode of transportation in the STP

a i = the amount of products available at source i

b j = the demand for the product at destination j

e k = the maximum amount of product that can be transported using conveyance k

The determination of the size of the fleet for each type of truck that is dispatched daily from each factory to all destinations for the transportation of various products is expressed formally as follows:

z ik denotes the number of trucks of type k that are dispatched daily from factory i .

C k represents the capacity of truck k in terms of the number of pallets it can transport.

x ijk denotes a binary decision variable that is set to one if truck k is dispatched from factory i to destination j to transport product p , and zero otherwise. The summation is performed over all destinations j and all products p .

This case study focuses on an Egyptian manufacturing company that produces over 70,000 pallets of various water and carbonated products daily. The company has 25 main distribution centers and eight factories located in different industrial cities in Egypt. The company’s transportation fleet consists of hundreds of trucks with varying capacities that are used to transport products from factories to distribution centers. The trucks have been classified into three types (type A, type B, and type C) based on their capacities. The company produces three different types of products that are packaged in pallets. It was observed that the sizes and weights of the pallets are consistent across all product types The main objective of this case study is to determine the minimum number of each truck type required in the manufacturer’s garage to minimize fuel consumption costs and reduce product delivery time.

The problem was addressed by analyzing the benefits of diversifying trucks and implementing the solid transport method. Subsequently, the problem was resolved while considering the capacities of the sources and the requirements of the destinations. The scenario involved shipping products using a single type of truck, and the fuel consumption costs were calculated accordingly. The first objective was to reduce the cost of fuel consumption on the one-way journey from the factories to the distribution centers. The second objective was to reduce the time of arrival of the products to the destinations. The time was calculated based on the average speed of the trucks in the company’s records, which varies depending on the weight and size of the transported goods.

To address the multiple objectives and the uncertainty in supply and demand, an approach was adopted to determine the minimum number of trucks required at each factory. This approach involved determining the maximum number of trucks of each type that should be present in each factory under all previous conditions. The study emphasizes the significance of achieving a balance between reducing transportation costs and time while ensuring trucks are capable of accommodating quantities of any size, thus avoiding underutilization.

Figure  1 presents the mean daily output, measured in pallets, for each factory across three distinct product types. Additionally, Fig.  2 displays the average daily demand, measured in pallets, for the distribution centers of the same three product types.

No. of pallets in each source

No. of pallets in each destination

Results and discussion

As a result of the case study, the single objective problems of time and fuel consumption cost have been solved. The next step is to prepare a model for the multi-objective multi-dimensional solid transportation problem. Prior to commencing, it is necessary to determine the upper and lower bounds for each objective.

Assuming the first objective is fuel consumption cost and the second objective is time, we calculate the upper and lower bounds as follows:

The lower bound for the first objective, “cost,” is generated from the optimal solution for its single-objective model, denoted as Z 1 ( x 1 ), and equals 70,165.50 L.E.

The lower bound for the second objective, “time,” is generated from the optimal solution for its single-objective model, denoted as Z 2 ( x 2 ), and equals 87,280 min.

The upper bound for the first objective is obtained by multiplying c ijkp for the second objective by x ijkp for the first objective. The resulting value is denoted as Z 1 ( x 2 ) and equals 73,027.50 L.E.

The upper bound for the second objective is obtained by multiplying t ijkp for the first objective by x ijkp for the second objective. The resulting value is denoted as Z 2 ( x 1 ) and equals 88,286.50 min.

As such, the aspiration levels for each objective are defined from the above values by evaluating the maximum and minimum value of each objective.

The aspiration level for the first objective, denoted as F 1, ranges between 70,165.50 and 73,027.50, i.e., 70,165.50 <  =  F 1 <  = 730,27.50.

The aspiration level for the second objective, denoted as F 2, ranges between 87,280 and 88,286.50, i.e., 87,280 <  =  F 2 <  = 88,286.50.

The objective function for the multi-objective multidimensional solid transport problem was determined using the Zimmermann Programming Technique, Global Criteria Method, and Minimum Distance Method. The first two methods directly provided the best compromise solution (BCS), while the last method generated non-dominated extreme points by assigning different weights to each objective and finding the BCS from them. The best compromise solution was obtained using the Lingo software [ 34 ]. Table 1 and Fig.  3 present the objective values for the optimal solutions of fuel consumption cost and time, the best compromise solution, and solutions with different weights for both objectives. Figure  4 illustrates the minimum required number of each type of truck for daily transportation of various products from sources to destinations.

Objective value in different cases

Ideal distribution of the company’s truck fleet

The primary objective of the case study is to determine the minimum number of trucks of each type required daily at each garage for transporting products from factories to distribution centers. The minimum number of trucks needs to be flexible, allowing decision-makers to make various choices, such as minimizing fuel consumption cost, delivery time, or achieving the best compromise between different objectives. To determine the minimum number of required trucks, we compare all the previously studied cases and select the largest number that satisfies the condition: min Zik (should be set) = max Zik (from different cases). Due to the discrepancy between the truck capacity and the quantity of products to be transported, the required number of trucks may have decimal places. In such cases, the fraction is rounded to the nearest whole number. For example, if the quantity of items from a location requires one and a half trucks, two trucks of the specified type are transported on the first day, one and a half trucks are distributed, and half a truck remains in stock at the distribution center. On the next day, only one truck is transferred to the same distribution center, along with the semi-truck left over from the previous day, and so on. This solution may be preferable to transporting trucks that are not at full capacity. Table 2 and Fig.  5 depict the ideal distribution of the company’s truck fleet under various optimization and multi-objective conditions.

Min. No. of trucks should be set for different cases

Conclusions

In conclusion, this research paper addresses the critical issue of optimizing transportation within the context of logistics and supply chain management, specifically focusing on the methods known as the solid transportation problem (STP) and the multi-dimensional solid transportation problem (MDSTP). The study presents a case study conducted on a private sector company in Egypt to determine the optimal distribution of its truck fleet under different optimization and multi-objective conditions.

The research utilizes the multi-objective multi-dimensional solid transportation problem (MOMDSTP) to identify the best compromise solution, taking into account fuel consumption costs and total shipping time. Three decision-making methods, namely the Zimmermann Programming Technique, the Global Criteria Method, and the Minimum Distance Method, are employed to derive optimal solutions for the objectives.

The findings of this study make a significant contribution to the development of approaches for solving multi-objective solid transportation problems with uncertain parameters. The research addresses the complexities of diverse truck fleets and transported products by incorporating fuzzy programming, uncertainty theory, and related concepts. It critically examines the limitations of previous approaches that often focused solely on single-objective solutions and overlooked specific constraints.

The primary objective of this research is to determine the minimum number of trucks required to fulfill decision-makers objectives while optimizing fuel consumption and transportation timeliness. The proposed approach combines the framework of the multi-dimensional solid transportation problem with a multi-objective optimization technique, offering comprehensive solutions for decision-makers with multiple priorities.

This study provides practical solutions for real-world transportation scenarios and demonstrates the potential for enhancing transportation efficiency and cost-effectiveness in various industries or contexts. The comparative analysis of the proposed work highlights the advancements and novelty introduced by the approach, emphasizing its significant contributions to the field of transportation problem research.

Future research should explore additional dimensions of the multi-objective solid transportation problem and incorporate other decision-making methods or optimization techniques. Additionally, incorporating uncertainty analysis and sensitivity analysis can enhance the robustness and reliability of the proposed solutions. Investigating the applicability of the approach in diverse geographical contexts or industries would yield further insights and broaden the potential applications of the research findings.

Availability of data and materials

The data that support the findings of this study are available from the company but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. Data are however available from the authors upon reasonable request. Please note that some data has been mentioned in the form of charts as agreed with the company.

Abbreviations

Solid transportation problem

Multi-objective solid transportation problems

Multi-dimensional solid transportation problem

Multi-objective multi-dimensional solid transportation problem

Best compromise solution

Taha HA (2013) Operations research: an introduction. Pearson Education India

Li T et al (2020) Federated optimization in heterogeneous networks. Proc Mach Learn Syst 2:429–450

Google Scholar  

Babu MA et al (2020) A brief overview of the classical transportation problem.

Winston WL (2022) Operations research: applications and algorithms. Cengage Learning

Pratihar J et al (2020) Transportation problem in neutrosophic environment, in Neutrosophic graph theory and algorithms. IGI Global, p 180–212

Guo G, Obłój J (2019) Computational methods for martingale optimal transport problems. Ann Appl Probab 29(6):3311–3347

Article   MathSciNet   MATH   Google Scholar  

Marwan M (2022) Optimasi biaya distribusi material Dengan Metode NWC (North West Corner) DAN Metode VAM (Vogel Approximation Method) PADA PT XYZ. IESM J (Indust Eng Syst Manage J) 2(2):137–146

Qiuping N et al (2023) A parametric neutrosophic model for the solid transportation problem. Manag Decis 61(2):421–442

Article   Google Scholar  

Singh S, Tuli R, Sarode D (2017) A review on fuzzy and stochastic extensions of the multi index transportation problem. Yugoslav J Oper Res 27(1):3–29

Baidya A, Bera UK (2019) Solid transportation problem under fully fuzzy environment. Int J Math Oper Res 15(4):498–539

Berbatov K et al (2022) Diffusion in multi-dimensional solids using Forman’s combinatorial differential forms. Appl Math Model 110:172–192

Carlier G (2003) On a class of multidimensional optimal transportation problems. J Convex Anal 10(2):517–530

MathSciNet   MATH   Google Scholar  

Zaki SA et al (2012) Efficient multiobjective genetic algorithm for solving transportation, assignment, and transshipment problems. Appl Math 03(01):92–99

Article   MathSciNet   Google Scholar  

Latpate R, Kurade SS (2022) Multi-objective multi-index transportation model for crude oil using fuzzy NSGA-II. IEEE Trans Intell Transp Syst 23(2):1347–1356

Bélanger V, Ruiz A, Soriano P (2019) Recent optimization models and trends in location, relocation, and dispatching of emergency medical vehicles. Eur J Oper Res 272(1):1–23

Kar MB et al (2018) A multi-objective multi-item solid transportation problem with vehicle cost, volume and weight capacity under fuzzy environment. J Intell Fuzzy Syst 35(2):1991–1999

Mirmohseni SM, Nasseri SH, Zabihi A (2017) An interactive possibilistic programming for fuzzy multi objective solid transportation problem. Appl Math Sci 11:2209–2217

Kakran VY, Dhodiya JM (2021) Multi-objective capacitated solid transportation problem with uncertain variables. Int J Math, Eng Manage Sci 6(5):1406–1422

MATH   Google Scholar  

Chen L, Peng J, Zhang B (2017) Uncertain goal programming models for bicriteria solid transportation problem. Appl Soft Comput 51:49–59

Khalifa HAE-W, Kumar P, Alharbi MG (2021) On characterizing solution for multi-objective fractional two-stage solid transportation problem under fuzzy environment. J Intell Syst 30(1):620–635

El-Shorbagy MA et al (2020) Evolutionary algorithm for multi-objective multi-index transportation problem under fuzziness. J Appl Res Ind Eng 7(1):36–56

Uddin MS et al (2021) Goal programming tactic for uncertain multi-objective transportation problem using fuzzy linear membership function. Alex Eng J 60(2):2525–2533

Hosseinzadeh E (2023) A solution procedure to solve multi-objective linear fractional programming problem in neutrosophic fuzzy environment . J Mahani Math Res. 111–126.  https://jmmrc.uk.ac.ir/article_3728_bc0be59dc0f595cc32faae1991cd12f9.pdf

Jagtap K, and Kawale S (2017) Multi-Dimensional-Multi-Objective-Transportation-Problem-by-Goal-Programming . Int J Sci Eng Res 8(6):568–573

Paratne P, and Bit A (2019) Fuzzy programming technique with new exponential membership function for the solution of multiobjective transportation problem with mixed constraints. J Emerg Technol Innov Res.  https://www.researchgate.net/profile/Mohammed-Rabie-3/publication/363480949_A_case_study_on_the_optimization_of_multi-objective_functions_transportation_model_for_public_transport_authority_Egypt/links/631f0549071ea12e362a9214/A-case-study-on-the-optimization-of-multi-objective-functions-transportation-model-for-public-transport-authority-Egypt.pdf

Annamalaınatarajan R, and Swaminathan M (2021) Uncertain multi–objective multi–item four dimensional fractional transportation model . Ann Rom Soc Cell Biol. 231–247.  https://www.annalsofrscb.ro/index.php/journal/article/download/2457/2063

Mohammed A (2020) Towards a sustainable assessment of suppliers: an integrated fuzzy TOPSIS-possibilistic multi-objective approach. Ann Oper Res 293:639–668

Umarusman N (2019) Using global criterion method to define priorities in Lexicographic goal programming and an application for optimal system design . MANAS Sosyal Araştırmalar Dergisi. 8(1):326–341

Kamal M et al (2018) A distance based method for solving multi-objective optimization problems . J Mod Appl Stat Methods 17(1).  https://digitalcommons.wayne.edu/jmasm/vol17/iss1/21

Kaur L, Rakshit M, Singh S (2018) A new approach to solve multi-objective transportation problem. Appl Appl Math: Int J (AAM) 13(1):10

Kamal M et al (2018) A distance based method for solving multi-objective optimization problems. J Mod Appl Stat Methods 17(1):21

Yang L, Feng Y (2007) A bicriteria solid transportation problem with fixed charge under stochastic environment. Appl Math Model 31(12):2668–2683

Article   MATH   Google Scholar  

Munot DA, Ghadle KP (2022) A GM method for solving solid transportation problem. J Algebraic Stat 13(3):4841–4846

Gupta N, and Ali I (2021) Optimization with LINGO-18 problems and applications. CRC Press

Download references

Acknowledgements

Not applicable.

Author information

Authors and affiliations.

Automotive and Tractor Engineering Department, Minia University, Minia, Egypt

Mohamed H. Abdelati, Ali M. Abd-El-Tawwab & M Rabie

Automotive and Tractor Engineering Department, Helwan University, Mataria, Egypt

Elsayed Elsayed M. Ellimony

You can also search for this author in PubMed   Google Scholar

Contributions

MHA designed the research study, conducted data collection, analyzed the data, contributed to the writing of the paper, and reviewed and edited the final manuscript. AMA contributed to the design of the research study, conducted a literature review, analyzed the data, contributed to the writing of the paper, and reviewed and edited the final manuscript. EEME contributed to the design of the research study, conducted data collection, analyzed the data, contributed to the writing of the paper, and reviewed and edited the final manuscript.MR contributed to the design of the research study, conducted programming using Lingo software and others, analyzed the data, contributed to the writing of the paper, and reviewed and edited the final manuscript. All authors have read and approved the manuscript.

Corresponding author

Correspondence to Mohamed H. Abdelati .

Ethics declarations

Competing interests.

The authors declare that they have no competing interests.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Abdelati, M.H., Abd-El-Tawwab, A.M., Ellimony, E.E.M. et al. Solving a multi-objective solid transportation problem: a comparative study of alternative methods for decision-making. J. Eng. Appl. Sci. 70 , 82 (2023). https://doi.org/10.1186/s44147-023-00247-z

Download citation

Received : 19 April 2023

Accepted : 27 June 2023

Published : 20 July 2023

DOI : https://doi.org/10.1186/s44147-023-00247-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Decision-making
• Multi-objective
• Solid transpiration