
- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
Table of Contents
Last modified on May 27th, 2024

#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline
Intermediate value theorem.
The intermediate value theorem (IVT) is about continuous functions in calculus. It states that if a function f(x) is continuous on the closed interval [a, b] and has two values f(a) and f(b) at the endpoints of the interval, then there is at least one value on [a, b] that lies between f(a) and f(b).
Mathematically, the IVT is written as:
- The curve y = f(x) is continuous on [a, b]
- ‘k’ is a number that lies between f(a) and f(b)
Then,
- There is at least one value ‘c’ such that c Є (a, b) and f(c) = k
Thus, the function y = f(x) at some point k = f(c) where either f(a) < k < f(b) or f(b) < k < f(a), which means a < c < b or b < c < a.
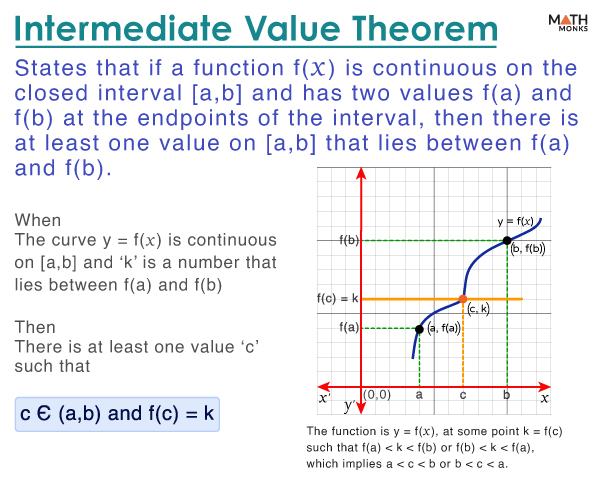
Here, the graph of y = f(x) is drawn in a continuous way within the interval [a, b], and thus, f(x) is continuous on [a, b]. In addition, if a value ‘c’ exists within the interval [a, b] such that c Є (a, b), then f(c) = k and f(a) < f(c) < f(b).
Since there exists ‘at least one value’ within the given interval, there can be more.
For example, there are three points where f(x) = k, as shown.
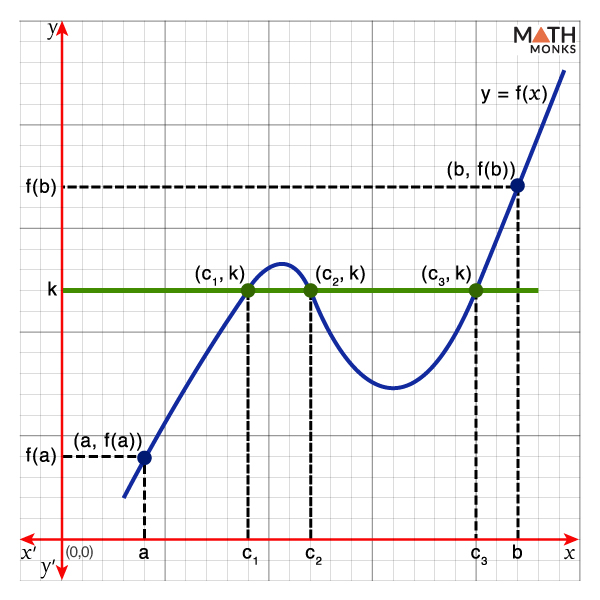
In the graph, f(c 1 ) = f(c 2 ) = f(c 3 ) = k, which means there are three values ‘c 1 ,’ ‘c 2 ,’ and ‘c 3 ’ on [a, b] with the function value ‘k.’
In particular, when c = 0, the intermediate value theorem is called Bolzano’s theorem (after its discoverer, Bernard Bolzano) or the Intermediate Zero Theorem .
To prove the IVT, we use the limit definition.
Without loss of generality, let us assume that f(a) < k < f(b) and a set A = {x Є [a, b]: f(x) < k}
Here, the set ‘A’ is non-empty since a Є A and f(a) < k, and also, ‘A’ is bounded above by ‘b.’
Thus, by completeness property, it has a supremum, say ‘c,’ which is greater than or equal to each element of ‘A’ and f(c) = k.
Proving c Є (a, b)
Since the function f(x) is continuous at ‘a’ and ‘b,’ f(c) ≠ a and f(c) ≠ b and thus c Є (a, b)
Proving f(c) = k
To prove f(c) = k, we verify both f(c) ≤ k and f(c) ≥ k.
Proving f(c) ≤ k
Since ‘c’ is the supremum, from the extreme value theorem, we get a sequence x n Є A where x n → c
Since f(x) is continuous, so f(x n ) → f(c)
Again, since x n Є A, by definition of ‘A,’ f(x n ) < k
⇒ f(c) = ${\lim _{n\rightarrow \infty }f\left( x_{n}\right) \leq k}$
Thus, f(c) ≤ k is proved …..(i)
Proving f(c) ≥ k:
Since c < b, thus for a very small ‘n,’ t n = ${c+\dfrac{1}{n} <b}$
⇒ t n > c
⇒ t n > supremum of ‘A’
Thus, f(t n ) ≥ k
Since ‘n’ is considered to be very small and f(x) is continuous, so f(t n ) → f(c), which implies
f(c) = ${\lim _{n\rightarrow \infty }f\left( t_{n}\right) \geq k}$
Thus, f(c) ≥ k is proved …..(ii)
From (i) and (ii), we conclude that f(c) = k
Thus, the intermediate value theorem is proved.
Verifying the Roots in an Interval
The intermediate value theorem is used to verify the existence of an equation’s root in a given interval, which shows whether the given function has its zero (or f(x) = 0) within the interval (a, b).
Let us verify this statement using the function f(x) = x 4 – 2x 3 + 3x – 21, which has a zero within the interval [1, 3]
Step 1: Finding f(a) and f(b)
Here, the given interval is [1, 3]
Calculating f(1) and f(3), we get
At x = 1, f(1) = (1) 4 – 2(1) 3 + 3(1) – 21 = -19
At x = 3, f(3) = (3) 4 – 2(3) 3 + 3(3) – 21 = 15
Step 2: Verifying
Since f(1) is negative, the curve is below zero at x = 1. Similarly, since f(3) is positive, the curve is above zero at x = 3.
Also, as f(x) is a polynomial function, it is continuous.
Now, by the intermediate value theorem, we conclude that the curve must pass through some point ‘c’ (say) within [1, 3] such that f(c) = 0
Hence, there exists a solution to the function f(x) = x 4 – 2x 3 + 3x – 21 on [1, 3] such that f(x) = 0
Limitations
However, we can only verify whether the function has a root in the given interval using the intermediate value theorem. We cannot find the number of roots or their values from it.
Considering the previous example, f(x) = x 4 – 2x 3 + 3x – 21, which has some root ‘c’ within [1, 3] such that f(c) = 0.
Thus, from the intermediate value theorem, the function f(x) = x 4 – 2x 3 + 3x – 21 has some roots, but the number of roots and their values cannot be obtained.
In addition to its theoretical applications, the intermediate value theorem has many real-life applications. One of them, ‘The Mystery of the Wobbly Table,’ is discussed.
Fixing a Wobbly Table
The intermediate value theorem helps to fix a wobbly table.
Here is an example of uneven ground causing a wobbly table. If the ground is continuous, and poorly fitted tiles cause no ups and downs, we rotate the table to fix the problem.
In a wobbly table, where three legs touch the ground, and the fourth leg is disturbed due to poorly fitted tiles, we can solve the issue using the intermediate value theorem. According to the theorem, there is a point where the fourth leg touches the ground perfectly. Finding the point will help us fix the issue.
It is based on the assumption that if we rotate a table and the 4 th leg goes inside the ground, then at some point, it will be above the ground, and at another point, it will be below the ground.
Mean Value Theorem vs. Intermediate Value Theorem
- The mean value theorem applies to differentiable functions and their derivatives, whereas the intermediate theorem applies to continuous functions.
- The mean value theorem guarantees the derivatives with certain values, whereas the intermediate value theorem confirms that the function has certain values between two given points within the interval.
Solved Example
Use the intermediate value theorem to verify whether the function f(x) = x 6 – x 3 – 3 has any roots in the interval [0, 2]
Here, the function is f(x) = x 6 – x 3 – 3 in the interval [0, 2] Calculating f(0) and f(2), we get At x = 0, f(0) = (0) 6 – (0) 3 – 3 = -3 At x = 2, f(2) = (2) 6 – (2) 3 – 3 = 53 Since f(0) is negative and f(2) is positive, the curve is below zero at x = 0 and above zero at x = 2. Also, since f(x) is a polynomial, it is continuous. Thus, by the intermediate value theorem, we conclude that the function f(x) = x 6 – x 3 – 3 has some roots on [0, 2] for which f(x) = 0.
- Mean Value Theorem
- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.
Intermediate Value Theorem
The idea behind the Intermediate Value Theorem is this:
one point below the line the other point above the line
then there is at least one place where the curve crosses the line!
Well of course we must cross the line to get from A to B!
Now that you know the idea , let's look more closely at the details.
The curve must be continuous ... no gaps or jumps in it.
Continuous is a special term with an exact definition in calculus, but here we will use this simplified definition:
More Formal
Here is the Intermediate Value Theorem stated more formally:
- The curve is the function y = f(x) ,
- which is continuous on the interval [a, b],
- and w is a number between f(a) and f(b),
... there must be at least one value c within [a, b] such that f(c) = w
In other words the function y = f(x) at some point must be w = f(c)
Notice that:
- w is between f(a) and f(b), which leads to ...
- c must be between a and b
At Least One
It also says "at least one value c", which means we could have more.
Here, for example, are 3 points where f(x)=w:
How Is This Useful?
Whenever we can show that:
- there is a point above some line
- and a point below that line, and
- that the curve is continuous,
we can then safely say "yes, there is a value somewhere in between that is on the line".
Example: is there a solution to x 5 − 2x 3 − 2 = 0 between x=0 and x=2?
0 5 − 2 × 0 3 − 2 = − 2
At x=2:
2 5 − 2 × 2 3 − 2 = 14
Now we know:
- at x=0, the curve is below zero
- at x=2, the curve is above zero
And, being a polynomial, the curve will be continuous,
so somewhere in between the curve must cross through y=0
Yes, there is a solution to x 5 − 2x 3 − 2 = 0 in the interval [0, 2]
An Interesting Thing!
The intermediate value theorem can fix a wobbly table.
| If your table is wobbly because of uneven ground ... ... just to fix it! The ground must be continuous (no steps such as poorly laid tiles). |
Why does this work?
We can always have 3 legs on the ground, it is the 4th leg that is the trouble.
Imagine we are rotating the table , and the 4th leg could somehow go into the ground (like sand):
- at some point it will be above the ground
- at another point it will be below the ground
So there must be some point where the 4th leg perfectly touches the ground and the table won't wobble.
(The famous Martin Gardner wrote about this in Scientific American. There is also a very complicated proof somewhere).
Another One
(It only works if you don't start at the highest or lowest point.)
The idea is:
- at some point you will be higher than where you started
- at another point you will be lower than where you started
So there must be a point in between where you are exactly as high as where you started.
Oh, and your path must be continuous , no disappearing and reappearing somewhere else.
The same thing happens with temperature, pressure, and so on.
And There's More!
If you follow a circular path ... somewhere on that circle there will be points that are:
- directly opposite each other
- and at the same height!
Can you think of more examples?
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
AP®︎/College Calculus AB
Course: ap®︎/college calculus ab > unit 1, intermediate value theorem.
- Worked example: using the intermediate value theorem
- Using the intermediate value theorem
- Justification with the intermediate value theorem: table
- Justification with the intermediate value theorem: equation
- Justification with the intermediate value theorem
- Intermediate value theorem review
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Video transcript
Reset password New user? Sign up
Existing user? Log in
Intermediate Value Theorem
Already have an account? Log in here.
- Khang Nguyen Thanh
- Ishan Singh
- Christopher Williams
- Akshay Sharma
- Satyabrata Dash
- Mahindra Jain
- A Former Brilliant Member
The intermediate value theorem states that if a continuous function attains two values, it must also attain all values in between these two values. Intuitively, a continuous function is a function whose graph can be drawn "without lifting pencil from paper." For instance, if \(f(x)\) is a continuous function that connects the points \([0,0]\) and \([5,20]\), then there must be some \(x_a\) between \(0\) and \(5\) where \(y=1,\) also some \(x_b\) where \(y=19\), another \(x_c\) where \(y= \frac{19}{5}\), etc. For this function there is an \(x\in [0,5]\) for any \(y\) value between \(0\) and \(20\).
Intermediate Value Theorem For two real numbers \(a\) and \(b\) with \(a < b\), let \(f\) be a continuous function on the closed interval \([a, b].\) Then for every \(y_0\) between \(f(a)\) and \(f(b),\) there exists a number \(x_0\in [a, b]\) with \(f(x_0)=y_0\).
A continuous function attaining the values \(f(a)\) and \(f(b)\) also attains all values in between.
The idea of the proof is as follows: take the two points \(\big(a,f(a)\big)\) and \(\big(b,f(b)\big)\) on the graph of the continuous function \(f: [a,b] \to \mathbb{R}\). These points demarcate a segment of the graph which connects the two points, as in the picture above. Since this segment has no holes or breaks in it (by continuity of the function), it must pass through each "level curve" \(y=c,\) where \(\min\big(f(a), f(b)\big) \le c \le \max\big(f(a), f(b)\big) \).
Note that the \(x_0\) guaranteed by the theorem may not be unique; the theorem implies that there is at least one \(x_0\) such that \(f(x_0) = y_0,\) but there may be more than one, depending on \(f\) and \(y_0.\)
Common Misinterpretations
Examples and applications, proofs of the intermediate value theorem.
The statement of the theorem has multiple requirements, all of which are necessary for the conclusion to hold. Here is an illustrative example:
For the function \(f(x) = x^2 - \frac{9}{x} + 1\), over which of the following intervals does the intermediate value theorem guarantee a root: \[\begin{array} &\left[-3, -1\right], &\left[-1, 1\right], &\left[1, 3\right]? \end{array}\] In order for the intermediate value theorem to guarantee a root on a specified interval \(\left[a, b\right]\), not only must the function \(f\) be continuous on the interval, but 0 must be contained between \(f(a)\) and \(f(b).\) Let's check the values of \(f(-3), f(-1), f(1),\) and \(f(3):\) \[\begin{array} &f(-3) = 13, &f(-1) = 11, &f(1) = -7, &f(3) = 7. \end{array} \] For the first interval \(\left[-3, -1\right],\) the values returned by \(f\) are both positive which do not sandwich 0, meaning the intermediate value theorem does not guarantee a root. For the second interval \(\left[-1, 1\right],\) the values returned by \(f\) are on either side of 0, which seems to suggest that \(f\) has a root on the interval \(\left[-1, 1\right].\) However, it's important to note that \(f(x)\) has a discontinuity at \(x = 0,\) meaning the intermediate value theorem does not hold. Indeed, \(f(x)\) does not have an \(x\)-intercept on the interval \(\left[-1, 1\right].\) For the last interval \(\left[1, 3\right],\) the values returned by \(f\) are on either side of 0, which implies that \(f\) has a root on the interval \(\left[1, 3\right].\) This is confirmed by the intermediate value theorem because \(f\) is continuous on \(\left[1, 3\right].\) \(_\square\) Graph of f(x)
As in the above example, one simple and important use of the intermediate value theorem (hereafter referred to as IVT) is to prove that certain equations have solutions. Consider the following example:
Does the equation \(\cos x = x\) have solution(s) \(x\in \mathbb{R}\)? If so, how many solutions does it have? We study the function \(f(x) = x-\cos x\). Note that \(f(0) = -1 < 0\) and \(f(\pi) = \pi + 1 > 0\). Thus, by the IVT, there must be some \(y\in [0,\pi]\) such that \(f(y) = 0 \), i.e. \(y = \cos y\). One root of the equation has been identified. Is this the only root? Note that \(f'(x) = 1+\sin x\) is everywhere non-negative, so \(f\) is increasing monotonically. Hence, \(f\) can only have one root. \(_\square\)
Is there a solution to \(x^5 - 2 x^3 - 2 = 0,\) where \(x\in [0,2]?\) At \(x=0\), we have \(0^5 - 2 \times 0^3 - 2 = -2.\) At \(x=2\), we have \(2^5 - 2 \times 2^3 - 2 = 14.\) So the IVT implies that there is a solution to \(x^5 - 2 x^3 - 2 = 0\) in the interval \( [0, 2]\). \(_\square\)
Suppose that \(f\) is continuous on \([0, 1]\) and \(f(0) = f(1)\). Let \(n\) be any positive integer, then prove that there is some number \(x\) such that \[f(x) = f\left(x +\dfrac{1}{n}\right).\] Define \(g(x) = f(x) − f\left(x +\frac{1}{n}\right)\). Consider the set of numbers \(S =\left\{f(0), f\left(\frac{1}{n}\right), f\left(\frac{2}{n}\right), \ldots , f(1)\right\}\). Let \(k\) be such that \(f\left(\frac{k}{n}\right)\) is the largest number in \(S\). Suppose that \(k \ne 0\) and \(k \ne n\). Then \(g\left(\frac{k}{n}\right) = f\left(\frac{k}{n}\right) − f\left(\frac{k+1}{n}\right) \geq 0\), and \(g\left(\frac{k-1}{n}\right) = f\left(\frac{k-1}{n}\right) − f\left(\frac{k}{n}\right)\leq 0\). By the Intermediate value theorem, there is \(c\in \left[\frac{k-1}{n},\frac{k}{n}\right]\) with \(g(c) = 0\), so that \(f(c) − f\left(c + \frac{1}{n}\right) = 0\), or \(f(c) = f\left(c + \frac{1}{n}\right)\) as desired. Finally, if the largest number in \(S\) is \(f(0) = f(1)\), then the same argument works with \(k\) chosen such that \(f\left(\frac{k}{n}\right)\) is the minimum number in \(S\). \(_\square\) Note that if \(f(0)\) is both the largest and smallest number in \(S\), then they are all the same and \(f(0) = f\left(\frac{1}{n}\right)\).
Suppose that \(f\) is continuous on \([0, 1]\) and \(f(0) = f(1)\). Let \(\varepsilon\) be the hyperreal unit, then prove that there is some number \(x\) such that \[f(x) = f\left(x +\varepsilon \right).\] First, assume \(f(x)\) is not constant on \([0,1]\). The result holds trivially if it is. Then, let \(g(x)=f(x)-f(x+\varepsilon)\) Since \(f\) is not constant, there exists a \(c\in[0,1]\) such that \(f(c)\) is a maximum (or a minimum, but assume for now that it is a max; a min is handled similarly). Then, \(g(c) = f(c) - f(c+\varepsilon) \geq 0\) and \(g(c-\varepsilon) = f(c-\varepsilon) - f(c) \leq 0\) Now, by the Intermediate Value Theorem, if \(\varepsilon >0\), there exists a \(y\in[c-\varepsilon,c]\) such that \(g(y)=0\). \((\)If \(\varepsilon < 0, y\in[c,c-\varepsilon]\), instead.\()\) Thus, \(f(y) = f(y+\varepsilon)\), as wanted. If \(\varepsilon = 0\), \(f(x) = f(x+\varepsilon)\ \forall x\). \(_\square\)
Of the four statements below, which are true?
I. The equation \(x^4 -3x+ 1 = 0\) has a unique real solution. II. The equation \(\sin x = x\) has a unique real solution. III. The equation \(3x^5 - 20x^3 + 60x +16=0\) has a unique real solution. IV. The equation \(\tan x = x\) has a unique real solution.
A real-valued function \(f\) is said to have the intermediate value property if for every \( [a,b] \) in the domain of \(f\), and for every
\[x \in \Big[\min\big(f(a), f(b)\big), \max\big(f(a), f(b)\big)\Big],\]
there exists some \(c\in [a,b]\) such that \(f(c) = x\).
The intermediate value theorem states that if \(f\) is continuous, then \(f\) has the intermediate value property. Is the converse of this theorem true? That is, if a function has the intermediate value property, must it be continuous on its domain?
Since it can detect zeroes of functions, the IVT is an important tool for the analysis of continuous functions. However, through some clever contortions, IVT can give even more impressive results. For instance, one can prove the Borsuk-Ulam theorem in dimension 1. This theorem states that for any continuous real-valued function \(f\) on a circle, there is some point \(p\) on the circle such that \(f\) takes the same value at \(p\) and at the point on the circle directly opposite to \(p\) \((\)the antipode of \(p).\)
This implies that on any great circle of the globe, any continuously varying information will take on the same value at some two antipodal points. For instance, there must exist two antipodal points on the equator at which the air temperature is the same.
Let \(S^1\) denote a circle, and suppose that \(f: S^1 \to \mathbb{R}\) is a continuous function. Then, there exists \(\mathbf{x}\in S^1\) such that \(f(\mathbf{x}) = f(-\mathbf{x})\). Note: Here, by the circle \(S^1\), we mean the set of vectors in \(\mathbb{R}^2\) of length precisely 1. In other words, \(S^1\) is the set of points \((x,y) \in \mathbb{R}^2\) such that \(x^2 + y^2 = 1\).
There is a function \(p: [0,2\pi) \to S^1\) given by \(p(\theta) = (\cos \theta, \sin \theta)\). Composing this with \(f\) gives \(g:= f\circ p : [0,2\pi) \to \mathbb{R}\). Define a function \(h:[0,2\pi) \to \mathbb{R}\) by \[h(\theta) := g(\theta + \pi) - g(\theta),\] where we take \(\theta + \pi \pmod{2\pi}\) if \(\theta >\pi\). Note that \[h(0) = g(\pi) - g(0) = -\big(g(0) - g(\pi)\big) = -h(\pi).\] In particular, \(h(0)\) and \(h(\pi)\) have opposite signs. Thus, by the IVT, there is some \(t \in (0,\pi)\) such that \(h(t) = 0\). This means \(g(t + \pi) = g(t)\). Let \(\mathbf{x} = (\cos t, \sin t)\). Since \(p(t+\pi) = -\mathbf{x}\), we conclude \[f(-\mathbf{x}) = g(t+\pi) = g(t) = f(\mathbf{x})\] as desired. \(_\square\)
Any die is modeled by some polyhedron. If the polyhedron is completely symmetric in the sense that any face can be taken to any other face via a rigid motion, then the die will be fair; when the die is rolled, the probability of landing on any face will equal the probability of landing on any other face.
Do there exist fair dice that are not completely symmetric?
Hint : Start with a prism \(P\) whose cross-sections are regular \(n\)-gons. Now consider the dual polyhedron \(P^{\star}\), the polyhedron whose vertices are the centers of the faces of the original prism. This \(P^{\star}\) looks like two pyramids with regular \(n\)-gon cross-sections that have been glued together at their bases. Now, can you modify \(P^{\star}\) to obtain a fair die that isn't completely symmetric?
One standard proof of the intermediate value theorem uses the least upper bound property of the real numbers that every nonempty subset of \(\mathbb R\) with an upper bound has a least upper bound. This is an important property that helps characterize the real numbers—note that the rational numbers don't have the least upper bound property \(\big(\)consider e.g. the set of all rational numbers less than \(\sqrt{2}\big).\) For a discussion of this property, see the Infimum/Supremum wiki. Here is a proof of the intermediate value theorem using the least upper bound property.
Let \(f \colon [a,b] \to {\mathbb R}\) be a continuous function. Let \(y\) be a number between \(f(a)\) and \(f(b).\) Suppose without loss of generality that \( f(a) \le f(b), \) and consider \[S = \big\{ x \in [a,b] \colon f(z) \le y \text{ for all } z \in [a,x] \big\}.\] Then \( S \) is nonempty since \( a \in S,\) and it has an upper bound \((\)namely \( b), \) so there is a least upper bound. Call that least upper bound \( c. \) Suppose \( f(c) > y.\) Then let \( \epsilon = f(c) - y > 0.\) By continuity, there is a \( \delta >0 \) such that \( |x-c|<\delta \) implies \( |f(x)-f(c)|<\epsilon. \) But \( |f(x)-f(c)|<\epsilon \) implies \( f(x) > y \) for all \( x \) in that range, so no \( x\)'s in that range lie in \( S. \) So \( c-\delta \) is an upper bound for \( S \) as well, which is a contradiction of the "leastness" of \( c.\) Suppose \( f(c) < y \). Then let \( \epsilon = y-f(c) > 0.\) By continuity, there is a \( \delta>0 \) such that \( |x-c|<\delta \) implies \( |f(x)-f(c)|<\epsilon. \) But \( |f(x)-f(c)|<\epsilon\) implies \( f(x) < y \) for all \( x \) in that range, so every \( x \) in that range lies in \( S. \) So for instance \( x = c+\frac{\delta}2 \) is in \( S \), which is a contradiction since \( c \) is an upper bound. The conclusion is that \( f(c)=y,\) as desired. \(_\square\)
In fact, the intermediate value theorem is equivalent to the least upper bound property. Suppose the intermediate value theorem holds, and for a nonempty set \(S\) with an upper bound, consider the function \(f\) that takes the value \(1\) on all upper bounds of \(S\) and \(-1\) on the rest of \(\mathbb R.\) Then \(f\) is not continuous by the intermediate value theorem \((\)it takes on the values \(-1\) and \(1,\) but never \(0),\) and it is straightforward to show that a point \(x\) where \(f\) is discontinuous must be a least upper bound for \(S.\)
The intermediate value theorem can also be reframed and generalized in terms of connected sets in \(\mathbb R.\) Recall that a connected set is a set which is not a disjoint union of two open subsets. The continuous image of a connected set is connected, so the image of a continuous function on a closed interval is connected, and thus must contain every point between any two points in the image. Here is a formal translation of this idea, adapted from the wiki on connected sets:
Let \(f\colon [a,b] \to \mathbb R \) be a continuous function, and \( y\) any real number between \(f(a)\) and \(f(b).\) We want to show that there is a \(c \in [a,b] \) such that \(f(c) = y.\) Because \([a,b]\) is connected, the image of \(f\) is connected. If \( y \notin f\big([a,b]\big),\) then the sets \( \Big\{ (-\infty,y) \cap f\big([a,b]\big) \Big\} \) and \( \Big\{\big(y,\infty\big) \cap f\big([a,b]\big)\Big\}\) are disjoint nonempty sets which are open in the subspace topology on \(f\big([a,b]\big).\) And their union is \( f\big([a,b]\big),\) which is a contradiction. \(_\square\)
Note that the least upper bound property is used in a relatively subtle way: it is needed in order to prove that the domain, the closed interval \([a,b],\) is connected. Any proof of the intermediate value theorem must appeal to a property equivalent to the least upper bound property, which uses the completeness of the real numbers.
This framing in terms of connected subsets explains why the intermediate value theorem does not generalize easily to continuous functions whose image lies in \({\mathbb R}^n\) for \(n > 1\) \((\text{or in }\, {\mathbb C});\) the connected subsets of \(\mathbb R\) are just the intervals, but the connected subsets of \({\mathbb R}^n\) are potentially much more complicated.
Problem Loading...
Note Loading...
Set Loading...
- Number Theory
- Data Structures
- Cornerstones
Proof of the Intermediate Value Theorem
If $f(x)$ is continuous on $[a,b]$ and $k$ is strictly between $f(a)$ and $f(b)$, then there exists some $c$ in $(a,b)$ where $f(c)=k$.
Without loss of generality, let us assume that $k$ is between $f(a)$ and $f(b)$ in the following way: $f(a) \lt k \lt f(b)$. The case were $f(b) \lt k \lt f(a)$ is handled similarly.
Define a set $S = \{x \in [a,b] : f(x) \lt k\}$, and let $c$ be the supremum of $S$ (i.e., the smallest value that is greater than or equal to every value of $S$).
Note, due to continuity at $a$, we can keep $f(x)$ within any $\epsilon \gt 0$ of $f(a)$ by keeping $x$ sufficiently close to $a$. Since $f(a) \lt k$ is a strict inequality, consider the implication when $\epsilon$ is half the distance between $k$ and $f(a)$. No value sufficiently close to $a$ can then be greater than $k$, which means there are values larger than $a$ in $S$. Hence, $a$ cannot be the supremum $c$ -- some value to its right must be..
Likewise, due to the continuity at $b$, we can keep $f(x)$ within any $\epsilon \gt 0$ of $f(b)$ by keeping $x$ sufficiently close to $b$. Since $k \lt f(b)$ is a strict inequality, consider the similar implication when $\epsilon$ is half the distance between $k$ and $f(b)$. Every value sufficiently close to $b$ must then be greater than $k$, which means $b$ cannot be the supremum $c$ -- some value to its left must be.
With $c \ne a$ and $c \ne b$, but $c \in [a,b]$, it must be the case that $c$ is in $(a,b)$.
Now we hope to show that $f(c) = k$.
Since $f(x)$ is assumed to be continuous on $[a,b]$ and $c \in [a,b]$, we know that $\lim_{x \rightarrow c} f(x) = f(c)$. Thus, by the epsilon-delta definition, we know that for any $\epsilon > 0$, we can find a $\delta > 0$ so that (with the exception of $x=c$) whenever $c-\delta \lt x \lt c+\delta$, we must have $f(c) - \epsilon \lt f(x) \lt f(c) + \epsilon$.
Consider any such value $\epsilon \gt 0$ and the value of $\delta$ that goes with it.
Now that there must exist some $x_0 \in (c - \delta, c]$ where $f(x_0) \lt k$. If there wasn't, then $c$ would not have been the supremum of $S$ -- some value to the left of $c$ would have been.
However, since $c-\delta \lt x_0 \lt c+\delta$, we also know that $f(c) - \epsilon \lt f(x_0) \lt f(c) + \epsilon$. Note, that in the case not inferred by the continuity of $f$ (i.e., when $x = c$), this just says $f(c) - \epsilon < f(c) < f(c) + \epsilon$, which should be obvious.
Focusing on the left side of this string inequality, $f(c) - \epsilon \lt f(c)$, we add $\epsilon$ to both sides to obtain $f(c) \lt f(x_0) + \epsilon$. Remembering that $f(x_0) \lt k$ we have
There also must exist some $x_1 \in [c, c + \delta)$ where $f(x_1) \ge k$. If there wasn't, then $c$ would not have been the supremum of $S$ -- some value to the right of $c$ would have been.
However, since $c - \delta \lt x_1 \lt c + \delta$, we also know that $f(c) - \epsilon \lt f(x_1) \lt f(c) + \epsilon$. (As above, the case not inferred by the continuity of $f$ is an obvious one.)
Focusing on the right side of this string inequality, $f(x_1) \lt f(c) + \epsilon$, we subtract $\epsilon$ from both sides to obtain $f(x_1) - \epsilon \lt f(c)$. Remembering that $f(x_1) \ge k$ we have
Then combining $(1)$ and $(2)$, we have
However, the only way this holds for any $\epsilon \gt 0$, is for $f(c) = k$.
1.5: the Intermediate Value Theorem
$\newcommand{\R}{\mathbb R }$ $\newcommand{\N}{\mathbb N }$ $\newcommand{\Z}{\mathbb Z }$ $\newcommand{\bfa}{\mathbf a}$ $\newcommand{\bfb}{\mathbf b}$ $\newcommand{\bff}{\mathbf f}$ $\newcommand{\bfu}{\mathbf u}$ $\newcommand{\bfx}{\mathbf x}$ $\newcommand{\bfy}{\mathbf y}$ $\newcommand{\ep}{\varepsilon}$
The Intermediate Value Theorem
Definition, examples of path-connected the Intermediate Value Theorem Problems
Definition, examples of path-connected
The familiar Intermediate Value Theorem (abbreviated IVT ) in 1d applies to a continuous function $f$ whose domain is an interval.
To state an analogue of the IVT in higher dimensions, we need to figure out what kind of domains the theorem should apply to.
A condition that is easy to state, intuitively reasonable, and good enough for all our purposes is path-connectedness . Informally, a set $S\subset \R^n$ is path-connected if any two points in $S$ can be connected by a path that stays in $S$. More precisely:
Definition. A set $S\subset \R^n$ is path-connected if, for every pair of points $\bfx$ and $\bfy$ in $S$, \begin{equation}\label{pc1} \exists \mbox{ continuous }\ \gamma:[0,1]\to S, \mbox{ such that }\gamma(0) = \bfx, \qquad \gamma(1) = \bfy. \end{equation}
(As is usual with mathematics, different sources sometimes use different terms. For example, Folland uses the terms arcwise connected or pathwise connected in place of path-connected .)
We emphasize that a key point in the definition is that $\gamma(s)$ is required to belong to $S$ for all $s\in [0,1]$
In general, our position will be that we can recognize path-connectedness when we see it. For example, consider the pictures below:
The set above is clearly path-connected set, and the set below clearly is not.
Because we can easily determine whether a set is path-connected by looking at it, we will not often go to the trouble of giving a rigorous mathematical proof of path-conectedness. If for some reason we decide to prove it, then normally the main point of a proof will be to write down in mathematical language an argument that captures our geometric intuition.
Here are a couple of examples:
Example 1 . A ball $B(r,\bfa)$ is path-connected.
Our geometric intuition: This is clear, because if $\bfx, \bfy$ both belong to $B(r,\bfa)$, then from drawing a picture, we are confident that the straight line segment that starts at $\bfx$ and ends at $\bfy$ is a continuous path joining $\bfx$ to $\bfy$.
If we decide to prove it: then we can just write down the above idea using mathematical language. We can interpret straight line segment that starts at $\bfx$ and ends at $\bfy$ as the function of the form $$ \gamma(t) = \bfb +t {\bf m} \quad\mbox{ for vectors }\bfb, {\bf m}\in \R^n, $$ where we will choose $\bfb$ and $\bf m$ so that $\gamma$ satisfies $\gamma(0)=\bfx, \gamma(1) = \bfy$, as required. This leads to \begin{equation}\label{segment} \boxed{ \gamma(t) = \bfx + t(\bfy - \bfx) = (1-t) \bfx + t\bfy } \end{equation} We have to check 3 things:
- $\gamma:[0,1]\to \R^n$ is continuous -- obvious!
- $\gamma(0)=\bfx$ and $\gamma(1) = \bfy$ --- obvious!
- $\gamma(t)\in B(r,\bfa)$ for all $t\in [0,1]$. In other words, we have to show that $|\gamma(t) - \bfa|<r$ for all $t\in [0,1]$. This is not obvious, but since the (mental) picture is very convincing, we can be confident that it's actually true. In fact this is the case, because for $t\in [0,1]$, \begin{align*} |\gamma(t) - \bfa| &= |(1-t) \bfx + t\bfy - \bfa| &\mbox{(definiton of $\gamma(t)$)}\\ &= |(1-t) (\bfx-\bfa) + t(\bfy - \bfa)| &\mbox{(rewrite)}\\ &\le |(1-t) (\bfx-\bfa)| + |t(\bfy - \bfa)| &\mbox{(triangle ineq.)}\\ %&= %|1-t|\, |\bfx-\bfa| + |t|\ |\bfy - \bfa| &\mbox{(triangle ineq.)}\\ &< (1-t) r + t r = r &\mbox{ since $\bfx, \bfy \in B(r,\bfa)$}. \end{align*} Thus $B(r,\bfa)$ satisfies condition \eqref{pc1}, and hence it is path-connected.
Remark. The formula \eqref{segment} for a path corresponding to a straight-line segment that starts at $\bfx$ and ends at $\bfy$ appears very frequently in mathematics, and should be committed to memory.
Example 2 . If $S_1$ and $S_2$ are path-connected, and $S_1\cap S_2 \ne \emptyset$, then $S := S_1\cup S_2$ is path-connected.
Our geometric intuition: Consider any $\bfx$ and $\bfy$ in $S$.
To find a path connecting these two points, let $\bf z$ be an element of $S_1\cap S_2$.
Then since $\bf z$ and $\bfx$ both belong to either $S_1$ or $S_2$, we can find a continuous path connecting $\bfx$ to $\bf z$ that stays in that set, and hence in $S$.
Similarly we can find a continuous path connecting $\bf z$ to $\bfy$ that stays in $S$.
Now we can move continuously from $\bfx$ to $\bfy$, while staying inside $S$, by concatenating the paths, i.e. first following the continuous path from $\bfx$ to $\bf z$; then following the continuous path from $\bf z$ to $\bfy$.
In this way, we can find a path conecting any two points $\bfx$ and $\bfy$.
If we decide to prove it : we will just follow the above geometric intuition.
Suppose we are given any two points $\bfx, \bfy$ in $S_1\cup S_2$.
Fix a point ${\bf z}\in S_1\cap S_2$. Here we are using the hypothesis that $S_1\cap S_2\ne \emptyset$.
Since $\bfx$ belongs to either $S_1$ or $S_2$, and $\bf z$ belongs to both $S_1$ and $S_2$, it is clear that one of these two path-connected sets --- either $S_1$ or $S_2$ --- must contain both $\bfx$ and $\bf z$. Thus these two points can be connected by a path, say $\gamma_x$, that stays in this set, and hence inside $S = S_1\cup S_2$. That is, $$ \exists \mbox{ continuous }\gamma_x:[0,1]\to S \mbox{ such that }\gamma_x(0) = \bfx, \qquad \gamma_x(1) ={\bf z}. $$
By exactly the same reasoning, $$ \exists\mbox{ continuous }\gamma_y:[0,1]\to S \mbox{ such that }\gamma_y(0) = {\bf z}, \qquad \gamma_y(1) ={\bf y}. $$
Now we have to figure out how to write down our idea of joining the two paths together to obtain a single continuous function $\gamma:[0,1]\to S$ that starts that $\bfx$ and ends at $\bfy$. As a preliminary step, define $\widetilde \gamma:[0,2]\to S$ by \begin{equation}\label{tg} \widetilde \gamma(t) := \begin{cases} \gamma_x(t) &\mbox{ if }t\in [0,1]\\ \gamma_y(t-1) &\mbox{ if }t\in [1,2] \ . \end{cases} \end{equation} This satisfies $$ \widetilde \gamma\mbox{ is continuous}, \qquad \widetilde \gamma(0) = \bfx, \qquad \widetilde \gamma(2) = \bfy. $$ (The detailed $\ep-\delta$ proof of continuity is left as a practice problem for those who are interested.) The only problem is that we want a function that ends up at $\bfy$ at $t=1$ rather than $t=2$. But this is easy to fix, by defining $$ \gamma(t) := \widetilde \gamma(2t),\qquad t\in [0,1]. $$ Then $\gamma$ satisfies \eqref{pc1}. Since $\bfx$ and $\bfy$ were arbitrary points in $S = S_1\cup S_2$, it follows that $S$ is path-connected. $\quad \Box$
Having given the definition of path-connected and seen some examples, we now state an $n$-dimensional version of the Intermediate Value Theorem, for which path-connectedness is the main geometric hypothesis.
Theorem 1: the Intermediate Value Theorem. Assume that $S$ is a path-connected subset of $\R^n$ and that $f:S\to \R$ is continuous. If $\bfa, \bfb$ are points in $S$ and $$ \mbox{ either } f(\bfa) < t <f(\bfb), \qquad \mbox{ or }\quad f(\bfb) < t <f(\bfa), $$ then there exists a point ${\bf c} \in S$ such that $f({\bf c})=t$.
Because $S$ is path-connected, there exists a continuous $\gamma:[0,1]\to S$ such that $\gamma(0)=\bfa$ and $\gamma(1) = \bfb$.
Now define $\phi: [0,1]\to \R$ by $\phi = f\circ \gamma$.
Because both $f$ and $\gamma$ are continuous, we know that $\phi$ is continuous. Also, by hypothesis $$ \mbox{ either } \ \ \phi(0) = f(\bfa) < t <f(\bfb)= \phi(1) , \qquad \mbox{ or }\quad \phi(1) = f(\bfb) < t <f(\bfa) =\phi(0). $$ So the Intermediate Value Theorem for functions of a single variable implies that there exists $s\in [0,1]$ such that $\phi(s) = t$.
But since $\phi(s) = f(\gamma(s))$, if we define ${\bf c} := \gamma(s)$, then ${\bf c} \in S$ and $f({\bf c})=t$. This proves the existence of a point $\bf c$ with the desired properties. $\quad\Box$
As with functions of a single variable, the theorem can be used to show that certain equations have solutions. The following example is a little artificial but it illustrates this point.
Example 3 . Prove that the equation $$ x^2+2y^2 = e^{(z-\frac 12)^2 cos(e^{-\sin (y/(x+2))}) } $$ has a solution in the ball $B(2, {\bf 0})\subset \R^3$.
To solve this, let's rewrite the problem as $f(x,y,z)=0$ for $f(x,y,z) = x^2+2y^2 - e^{(z-\frac 12)^2 cos(e^{-\sin (y/(x+2))})}$. Note that $f(0,0,\frac 12) = -e^0 = -1 0$. Both of these points belong to $B(2,{\bf 0})$. We also know that balls are pathwise connected, so it follows from the Intermediate Value Theorem that there must exist some point in $B(2, {\bf 0})$ where $f=0$.
Example 4 Assume that $S$ is a subset of $\R^n$. The Intermediate Value Theorem implies if there exists a continuous function $f:S\to \R$ and a number $c\in \R$ and points $\bfa,\bfb\in S$ such that $$ f(\bfa)< c, \qquad f(\bfb)>c, \qquad f(\bfx)\ne c \mbox{ for any }\bfx\in S $$ then $S$ is not path-connected.
This can be used to prove that some sets $S$ are not path connected. For example, let $$ S := \{(x,y)\in \R^2 : x^2 - y^2 \ge 1 \}. $$ Let $f(x,y) = x$, and let $\bfa = (-1,0)$ and $\bfb= (1,0)$. Clearly $f(\bfa) = -1$ and $f(\bfb)=1$. But $S$ cannot contain any points where $f=0$, since $$ f(x,y)=0 \Rightarrow x=0 \Rightarrow x^2-y^2 = -y^2 \le 0 \Rightarrow (x,y)\not \in S. $$
Basic skills
Given an example of a set that is/is not path-connected
Determine (without proof) whether a given set is path-connected. For example, let $Q_j\subset \R^2$ denote the (open) $j$th quadrant, for $j=1,\ldots, 4$, so that $$ Q_1= \{(x,y)\in \R^2 : x>0\mbox{ and }y>0\}, \qquad Q_3= \{(x,y)\in \R^2 : x< 0\mbox{ and }y< 0\}, $$ Determine which of the following sets are path-connected:
- $Q_1\cup Q_3$
- $\bar Q_1 \cup Q_3$
- $\bar Q_1 \cup \bar Q_3$.
- $\partial Q_1\cup Q_3$.
Show that the equation $f(\bfx)= 0$ has a solution on the set $S = \cdots$. See Example 3 above. Strictly speaking, we should only ask this question when $S$ is a set that we have proved is path-connected, such as a ball.
More advanced/abstract questions
Prove that the function $\widetilde \gamma$, defined in \eqref{tg}, is continuous.
Detrmine whether a set is path-connected, and explain why your answer is correct. Consider for example the same sets appearing in the Basic Skills above. (Recall that in this class, explain means: give a mathematical argument that may fall short of a full proof but that commnunicates a basic relevant mathematical idea. In this case, to explain why a set is path-connected, you might for example describe, in words, how to connect any two points in a set by a continuous path, without writing down a formula for the path.)
If $S_1$ and $S_2$ are path-connected sets in $\R^2$, must it be true that $S_1\cap S_2$ is path-connected? Explain your answer.
A set $S\subset \R^n$ is defined to be star-shaped about the origin if, $$ \mbox{ for every $\bfx \in S$ and every $\lambda\in [0,1]$ }, \qquad\mbox{ the point }\lambda \bfx \mbox{ belongs to $S$}. $$
- Is a ball $B(r, {\bf 0})$ star-shaped about the origin?
- Draw a picture of a set $S \subset\R^2$ that is star-shaped about the origin and that contains the points $(10,0)$ and $(0,10)$, but not the point $(1,1)$.
- It is a fact that every set that is star-shaped about the origin is path-connected. Give a pictorial argument to explain why this is true.
- If you wish, prove that every set that is star-shaped about the origin is path-connected (presumably by converting your pictorial argument into a mathematical proof).
Let $$ S^+ := \{ \bfx = (x_1,\ldots, x_n)\in \R^n : |\bfx|=1, \ x_n \ge 0 \}. $$ and $$ S^- := \{ \bfx = (x_1,\ldots, x_n)\in \R^n : |\bfx|=1, \ x_n \le 0 \}. $$ One might call these sets the upper (unit) hemisphere and lower (unit) hemisphere respectively.
- Draw a picture of $S^+$ when $n=3$.
- Determine (without proof) whether $S^+$ is path-connected.
- If you wish, give a proof to show that your answer to the above question is correct. For this, it may be helpful to write a point $\ \bfx = (x_1,\ldots, x_n)\in S^+$ in the form $$ \bfx = (x_1,\ldots, x_{n-1}, f(x_1,\ldots, x_{n-1})) $$ where $$ x_1^2 +\ldots + x_{n-1}^2 \le 1, \quad\mbox{ and }\quad f(x_1,\ldots, x_{n-1}) =\sqrt{1- x_1^2 - \cdots -x_{n-1}^2}. $$
Let $S$ denote the unit sphere in $\R^n$: $$ S := \{ \bfx \in \R^n : |\bfx|=1, \}. $$
- Determine (without proof) whether $S$ is path-connected.
- If you wish, give a proof to show that your answer to the above question is correct.
Let $S$ denote the unit sphere in $\R^n$, as in the previous problem, and assume that $f:S\to \R$ is continuous. Prove that there exists some $\bfx\in S$ such that $f(\bfx) = f(-\bfx)$. (This implies, for example, that at any given moment, there are two exactly antipodal points on the earth where the temperature is exactly the same.) hints :
- Consider the function $g(\bfx) := f(\bfx) - f(-\bfx)$.
- If you have done the previous problem correctly, you now know that $S$ is pathwise connected. Use this fact in your solution.
$\Leftarrow$ $\Uparrow$ $\Rightarrow$
- Math Article
Intermediate Value Theorem

The intermediate value theorem is a theorem about continuous functions. Intermediate value theorem has its importance in Mathematics, especially in functional analysis. This theorem explains the virtues of continuity of a function . The two important cases of this theorem are widely used in Mathematics. Let us go ahead and learn about the intermediate value theorem and its two statements in this article.
Intermediate Value Theorem Statement
Intermediate value theorem states that if “f” be a continuous function over a closed interval [a, b] with its domain having values f(a) and f(b) at the endpoints of the interval, then the function takes any value between the values f(a) and f(b) at a point inside the interval. This theorem is explained in two different ways:
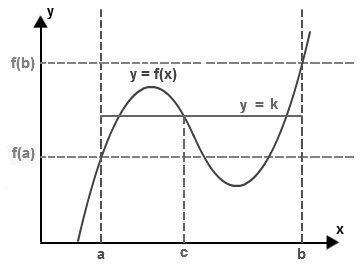
Statement 1:
If k is a value between f(a) and f(b), i.e.
either f(a) < k < f(b) or f(a) > k > f(b)
then there exists at least a number c within a to b i.e. c ∈ (a, b) in such a way that f(c) = k
Statement 2:
The set of images of function in interval [a, b], containing [f(a), f(b)] or [f(b), f(a)], i.e.
Theorem Explanation:
The statement of intermediate value theorem seems to be complicated. But it can be understood in simpler words. Let us consider the above diagram, there is a continuous function f with endpoints a and b, then the height of the point “a” and “b” would be “f(a)” and “f(b)”.
If we pick a height k between these heights f(a) and f(b), then according to this theorem, this line must intersect the function f at some point (say c), and this point must lie between a and b.
An intermediate value theorem, if c = 0, then it is referred to as Bolzano’s theorem .
Intermediate Theorem Proof
We are going to prove the first case of the first statement of the intermediate value theorem since the proof of the second one is similar.
We will prove this theorem by the use of completeness property of real numbers . The proof of “f(a) < k < f(b)” is given below:
Let us assume that A is the set of all the values of x in the interval [a, b], in such a way that f(x) ≤ k.
Here A is supposed to be a non-empty set as it has an element “a” and also A is bounded above by the value “b”.
Thus, by completeness property, we have that, “c” be the lowest value which is greater than or equal to each element of A. Hence, we can say that f(c) = k.
Given that f is continuous. Then let us consider a ε > 0, there exists “a δ > 0” such that
| f(x) – f(c) | < ε for every | x – c | < δ. This gives us
f(x) – ε < f(c) < f(x) + ε
For each x lying within c – δ and c + δ. So, we have values of x lying between c and c -δ, contained in A, such that :
f(c) < (f(x) + ε) ≤ (k + ε) ——– (1)
Similarly, values of x between c and c + δ that are not contained in A, such that
f(c) > (f(x) – ε) > (k − ε) ——–(2)
Combining both the inequality relations, obtain
k – ε < f(c) < k + ε
For every ε > 0
Hence, the theorem is proved.
Intermediate Theorem Applications
The intermediate value theorem has many applications. Mathematically, it is used in many areas. This theorem is utilized to prove that there exists a point below or above a given particular line. It is also used to analyze the continuity of a function that is continuous or not.
This theorem has many implications in Physics and Chemistry problems too. It is applicable whenever there is a continuously varying scalar quantity with endpoints sharing the same value for a variable. These quantities may be – pressure, temperature, elevation, carbon dioxide gas concentration, etc.
Intermediate value theorem has some significant real-life applications too. Let us take an example of a wobbly table due to the uneven ground. In order to fix this, rotate the table, provided that the ground is continuous; i.e. no ups and downs due to poorly-fitted tiles.
The wobbly table will have three of its legs touching the ground, while its fourth leg will be the problem. While rotating the table at a point, the fourth leg will be below the ground, and at some other point, it will lie above the ground. According to the intermediate value theorem, there will be a point at which the fourth leg will perfectly touch the ground, and the table is fixed.
Intermediate Theorem Example
Check whether there is a solution to the equation x 5 – 2x 3 -2 = 0 between the interval [0, 2].
Let us find the values of the given function at the x = 0 and x = 2.
f(x) = x 5 – 2x 3 -2 = 0
Substitute x = 0 in the given function
f(0) = (0) 5 – 2(0) 3 -2
Substitute x = 2 in the given function
f(2) = (2) 5 – 2(2) 3 -2
f(2) = 32 – 16 – 2
Therefore, we conclude that at x = 0, the curve is below zero; while at x = 2, it is above zero.
Since the given equation is a polynomial, its graph will be continuous.
Thus, applying the intermediate value theorem, we can say that the graph must cross at some point between (0, 2).
Hence, there exists a solution to the equation x 5 – 2x 3 -2 = 0 between the interval [0, 2].
Visit BYJU’s – The Learning App and download the app to explore all the important Maths-related videos to learn with ease.
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Intermediate Value Theorem
The intermediate value theorem (IVT) in calculus states that if a function f(x) is continuous over an interval [a, b], then the function takes on every value between f(a) and f(b). This theorem has very important applications like it is used:
- to verify whether there is a root of a given equation in a specified interval.
- to verify the existence of x-intercept of a function over a given interval, etc.
Let us learn more about the intermediate value theorem along with its proof and limitations along with examples.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What is Intermediate Value Theorem?
The intermediate value theorem (also known as IVT or IVT theorem) says that if a function f(x) is continuous on an interval [a, b], then for every y-value between f(a) and f(b), there exists some x-value in the interval (a, b). i.e., if f(x) is continuous on [a, b], then it should take every value that lies between f(a) and f(b). Recall that a continuous function is a function whose graph is a curve that can be drawn without lifting a pencil. Mathematically, this theorem is stated as follows:
Intermediate Value Theorem : "Suppose f(x) is a continuous function on [a, b] and L is a number that lies between f(a) and f(b), then there exists at least one 'c' such that c ∈ (a, b) (or a < c < b) and f(c) = L"
It is so obvious (because of continuity) how the theorem works and we can understand it from the following figure.
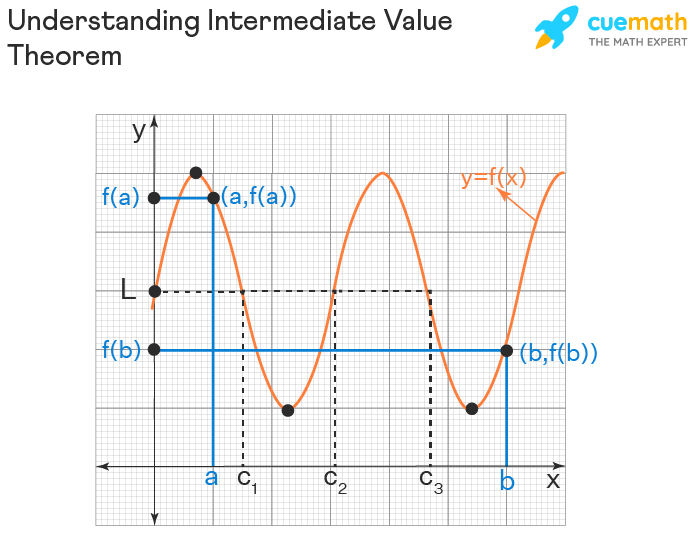
When the graph of f(x) can be drawn without lifting a pencil within the interval [a, b], it is so obvious that f(x) takes every value L that lies between f(a) and f(b). In fact, it is also possible that the equation f(c) = L can be possible for more than one value of 'c'. In the above figure, it is pretty clear that:
- f(c 1 ) = L
- f(c 2 ) = L
- f(c 3 ) = L
It means that there are three values c 1 , c 2 , and c 3 in the interval [a, b] whose function value is L.
Intermediate Value Theorem Proof
Though the proof of the intermediate value theorem is so pretty straight forward as mentioned earlier, here is the mathematical proof of the IVT theorem using the limit definition. Without loss of generality, assume that f(a) < L < f(b) and consider the following set :
A = { x ∈ [a, b]: f(x) < L}.
Notice that A is non-empty as a ∈ A (as f(a) < L) and also A is bounded above by 'b'.
Then it must have a supremum and let us assume it to be 'c'.
Proving c ∈ (a, b)
Because of the continuity of the function f(x) at 'a' and 'b', f(c) ≠ a and f(c) ≠ b.
Thus, c ∈ (a, b).
Proving f(c) = L
For this, we prove both f(c) ≤ L and f(c) ≥ L.
Proof of f(c) ≤ L:
Since 'c' is the supremum, by extreme value theorem , there is a sequence x n ∈ A with x n → c.
Since f(x) is continuous, f(x n ) → f(c).
But x n ∈ A, and by definition of A, f(x n ) < L.
⇒ f(c) = lim n → ∞ f(x n ) ≤ L.
Thus, we proved that f(c) ≤ L ... (1)
Proof of f(c) ≥ L:
Notice that c < b. Thus, for a very small 'n', t n = c + (1/n) < b.
Again, t n > c ⇒ t n > supremum of A. Thus, t n ∉ A.
Thus, f(t n ) ≥ L.
Since 'n' is very small and f(x) is continuous, f(t n ) → f(c). From this,
f(c) = lim n → ∞ f(t n ) ≥ L ... (2)
From (1) and (2), we have can conclude that f(c) = L.
Thus, the intermediate value theorem is proved.

Application of Intermediate Value Theorem
The important application of the intermediate value theorem is to verify the existence of a root of an equation in a given interval. In particular, the IVT theorem is used to see whether a given function has its zero ( x-intercept (or) f(x) = 0) within the given interval (a, b). To verify this, we follow the steps below:
- Step 1 : Find f(a) and f(b).
- Step 2 : If f(a) < 0 < f(b) (i.e., f(a) is negative and f(b) is positive) then f(x) has a zero (i.e., f(x) = 0) in the interval (a, b).
Let us examine the following example.
Example: Use the IVT to verify whether the function f(x) = x 3 - 3x - 19 has a zero in the interval [1, 5].
The interval is [1, 5]. Find f(1) and f(5).
f(1) = 1 3 - 3(1) - 19 = -21
f(5) = 5 3 - 3(5) - 19 = 91
Since f(1) is positive and f(5) is negative, by the intermediate value theorem, we can say that there must be some 'c' in [1, 5] such that f(c) = 0.
i.e., f(x) has a zero in the interval [1, 5].
Limitations of IVT Theorem
Observe the above example. Using the intermediate value theorem, we could only find whether the function f(x) has a root in the interval [1, 5]. But we couldn't find what root it is. Also, we couldn't verify how many roots f(x) has within the given interval (as we have seen in the figure of the first section , the function can take a value for more than one value of x). Further, there is one more limitation of the IVT theorem which can be understood from the example below:
Example: Use the intermediate value theorem to verify whether the equation 10 cos (x + 2) sin (x 2 ) = -6 has a root in the interval [0.5, 2]?
Let f(x) = 10 cos (x + 2) sin (x 2 ).
The given interval is [0.5, 2]. So we will find f(0.5) and f(2).
f(0.5) = 10 cos (0.5 + 2) sin (0.5 2 ) = -1.98
f(2) = 10 cos (2 + 2) sin (2 2 ) = 4.95
We wanted to know whether f(x) = -6 has a solution in the given interval. We can see that -6 does NOT lie between -1.98 and 4.95. What do the values of f(0.5) and f(2) tell about the existence of the root of f(x) = -6 in the given interval? Unfortunately, the intermediate value theorem does not mean anything in this case. This theorem can guarantee only whether the function takes the value, but it cannot guarantee about a value that a function cannot take.
Thus, in the above example, we cannot say using the IVT theorem that f(x) = -6 does NOT have a root in the interval [0.5, 2]. In fact, it has two roots (0.826 and 1.558) in the given interval as shown in the graph below.
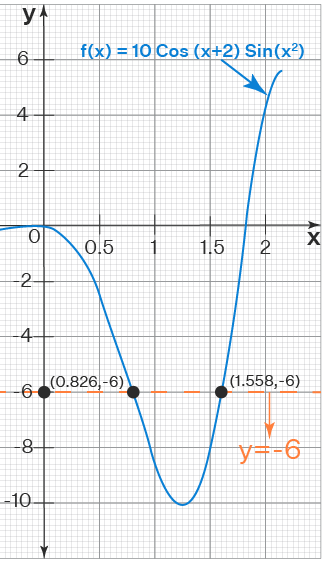
Important Notes on Intermediate Value Theorem:
- Using the intermediate value theorem, we can just know if the root exists; but it cannot guarantee if the root does not exist (see the above example).
- The IVT theorem cannot be applied when the function is NOT continuous.
- It does not help in finding the roots of an equation.
- We cannot say how many roots the equation has in the given interval using this theorem.
☛ Related Topics:
- Lagrange Mean Value Theorem
- Mean Value Theorem Formula
- Rolle's Theorem
Intermediate Value Theorem Examples
Example 1: Use the intermediate value theorem to verify whether a function f(x) = x + 1/x has a zero in the interval [-1, 1]?
The first condition to apply the IVT theorem is the function should be continuous in the given interval.
But the given function f(x) = x + 1/x is NOT continuous over [-1, 1] as f(0) is NOT defined here.
Thus, we cannot apply IVT here.
Answer: IVT cannot be applied here.
Example 2: Does the equation x 4 + 3x 2 - 2 = 0 has a solution in the interval [0, 1]? Explain your reasoning using IVT theorem.
Let us assume that f(x) = x 4 + 3x 2 - 2.
Since f(x) is a polynomial function , it is continuous.
We will find f(0) and f(1).
f(0) = 0 4 + 3(0) 2 - 2 = -2
f(1) = 1 4 + 3(1) 2 - 2 = 2
We want to know whether f(x) = 0 has any roots in the given interval. i.e., we have to see whether the function takes in the value 0. It is clear that -2 < 0 < 2 and hence by the intermediate value theorem, the given equation has at least one root in the given interval.
Answer: Yes, it has a root in [0, 1].
Example 3: Support your answer for Example 2 by graphing it.
In Example 2 , we have already proved by IVT that the given equation has a root in [0, 1]. Let us graph f(x) = x 4 + 3x 2 - 2 and see whether it has any roots (i.e., see whether it intersects the x-axis).

Since the graph cuts the x-axis at (0.749, 0), 0.749 is a root of the given function and it lies in the interval [0, 1].
Answer: The existence of the root is verified using the graph.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Intermediate Value Theorem
go to slide go to slide
FAQs on Intermediate Value Theorem
What is ivt calculus.
IVT ( Intermediate Value Theorem ) in calculus states that a function f(x) that is continuous on a specified interval [a, b] takes every value that is between f(a) and f(b). i.e., for any value 'L' lying between f(a) and f(b), there exists at least one value c such that a < c < b and f(c) = L.
How Do You Know When to Use Intermediate Value Theorem?
If we want to know whether a function has a root in the given interval, then we can use the intermediate value theorem. Note that this theorem only when the function is continuous.
Can the IVT Theorem be Applied for Discontinuous Functions?
No, the intermediate value theorem cannot be applied for discontinuous functions . Because "continuity" is what is making a function f(x) on an interval [a, b] to take any value between f(a) and f(b).
What are the Conditions of the Intermediate Value Theorem?
The conditions of IVT to apply on a function f(x) over an interval [a, b] are:
- f(x) should be continuous on [a, b]
- f(a) ≠ f(b)
When Cannot We Use Intermediate Value Theorem?
The intermediate value theorem :
- says "yes the function takes a value" if it really takes
- but it cannot say "no the function doesn't take a value" if it doesn't take
Thus, for a function f(x) that is continuous on [a, b], if a value L does not lie between f(a) and f(b), it is not always true that there is no value such that f(c) = L. Sometimes, there can be values of 'c' satisfying f(c) = L.
How Can We Find Zeros Using IVT Theorem?
IVT theorem is used just to verify if the function has a zero in the given interval. But it is neither used in finding the number of zeros nor used in finding the number of zeros .
What is the Difference Between Mean Value Theorem and Intermediate Value Theorem?
The mean value theorem talks about the differentiable and continuous functions and the intermediate value theorem talks only about the continuous functions. For more information, click here .
The Intermediate Value Theorem
We already know from the definition of continuity at a point that the graph of a function will not have a hole at any point where it is continuous. The Intermediate Value Theorem basically says that the graph of a continuous function on a closed interval will have no holes on that interval.
Statement of the Theorem
- Suppose $f(x)$ is continuous on the closed interval $[a,b]$. If $L$ is a real number between the values $f(a)$ and $f(b)$, but not equal to either of them, then there exists a number $c$ in the interval $[a,b]$. for which $f(c)=L$.
The graph on the left below illustrates the situation described by the theorem. Since the function $f(x)$ is continuous, the endpoints of the interval are connected by the graph, and the function will pass through all values between $f(a)$ and $f(b)$. The graph on the right below shows a function that is defined everywhere on the closed interval $[a,b]$, but is not continuous on that interval. The lack of continuity allows for values between $f(a)$ and $f(b)$ that the function never takes on.
Using the Intermediate Value Theorem
Show that the function $f(x)=x^{17}-3x^4+14$ is equal to 13 somewhere on the closed interval $[0,1]$.
| We note that $f(0)=14$ and $f(1)=12$, | By substituting the endpoints of the closed interval into the function, we obtain the values $f(a)$ and $f(b)$. |
| and $12 | |
| But $f(x)$ is a polynomial and is therefore continuous everywhere, so in particular it is continuous on the closed interval $[0,1]$. | The continuity of the function is the crux of the issue. Without it, the result could not be guaranteed. So we must demonstrate the continuity of the function on the given interval. And since the function is a polynomial, continuity is automatic. |
| Therefore, by the Intermediate Value Theorem, there exists a number $c$ in the interval $[0,1]$ for which $f(c)=13$. | Having verified all of the hypotheses of the Intermediate Value Theorem, the conclusion must then follow. |
Proof of the Theorem
Even though the statement of the Intermediate Value Theorem seems quite obvious, its proof is actually quite involved, and we have broken it down into several pieces. First, we will discuss the Completeness Axiom, upon which the theorem is based. Then we shall prove Bolzano's Theorem, which is a similar result for a somewhat simpler situation. Then the Intermediate Value Theorem will follow almost immediately.
The Completeness Axiom
Axioms are statements in a mathematical system that are assumed to be true without proof. The Completeness Axiom is an axiom about the real numbers, and is sometimes phrased in the language of least upper bounds. A real number $x$ is called a least upper bound for a set $S$ if the following two properties are true:
- The number $x$ is an upper bound for the set $S$. (In other words, if $s$ is any number in set $S$, then $s\le x$.)
- If $y
Note that it is not necessary for an upper bound to be in the set $S$. Both upper bounds and least upper bounds could be numbers outside of set $S$.
The statement of the Completeness Axiom is:
- If $S$ is a nonempty set of real numbers that is bounded above, then there exists exactly one real number that is the least upper bound of $S$.
To understand this, we shall consider a few examples.
- If set $S$ is the closed interval $[3,5]$, then the number 5 is the least upper bound. The value 5 is certainly an upper bound, since for every $s$ in the interval, $s\le 5$. And for any number $y<5$, there is a larger number that is still in the set $S$, namely 5 itself, so $y$ is not an upper bound. The Completeness Axiom states that 5 is the only least upper bound of this interval.
- If set $S$ is the open interval $(4,9)$, then the number 9 is the least upper bound. The value 9 is certainly an upper bound, since for every $s$ in the interval, $s\le 9$ (and in fact, $s$ is never equal to 9). And for any number $y<9$, there is a larger number that is still in the set $S$, namely $\dfrac{y+9}{2}$, so $y$ is not an upper bound. The Completeness Axiom states that 9 is the only least upper bound of this interval.
- If set $S$ is the interval $(6,\infty)$, then the hypothesis of the Completeness Axiom is not satisfied. In other words, set $S$ is not bounded above, because the values of $S$ continue on to infinity. Therefore, the conclusion of the Completeness Axiom is not guaranteed to follow. And in fact, in this case, the conclusion is not true, since there is no real number that is the least upper bound of this set.
- If set $S$ consists of the numbers of the sequence $a_n=\left\{\left. 7-\dfrac{1}{n} \right| n \text{ is a positive integer}\right\}$, then the number 7 is the least upper bound. The value 7 is certainly is an upper bound, since $7-\dfrac{1}{n}\le 7$ for all positive integers. And for any number $y \dfrac{1}{7-y}$. This inequality, when solved for $y$, yields $y<7-\dfrac{1}{n}$, so $y$ is not an upper bound. Thus, the Completeness Axiom states that 7 is the only least upper bound for this set.
Bolzano's Theorem
The statement of Bolzano's Theorem is:
- Suppose $f(x)$ is continuous on the closed interval $[a,b]$, and suppose that $f(a)$ and $f(b)$ have opposite signs. Then there exists a number $c$ in the interval $[a,b]$, for which $f(c)=0$.
| Since $f(a)$ and $f(b)$ have opposite signs, then one is positive and one is negative. Let us first suppose that $f(a) | The supposition of opposite signs also implies that neither value is zero itself. That leaves two cases, and we begin with one of them here. The other case will be dealt with later. |
| Define the set $S=\{x\in [a,b]|f(x)\le 0\}$. | This set contains all of the values of the function $f(x)$ on the closed interval $[a,b]$ for which the value of $f(x)$ is not positive. |
| The set $S$ is not empty, since $f(a) | |
| Therefore, $S$ has a least upper bound. Define the value $c$ to be the least upper bound of $S$. | Then we use the Completeness Axiom to establish the existence of the least upper bound, and we give it the name $c$. |
| Since $f(x)$ is continuous, then $\lim\limits_{x\to c}f(x)=f(c)$. | This is from the definition of continuity, which also states that each of those quantities is a real number. |
| Now, there are only three possibilities, either $f(c)>0$, or $f(c) | |
| So suppose $f(c)>0$. Let $\epsilon_1=\dfrac{f(c)}{2}$. Then $\epsilon_1>0$. | Beginning with the first of the three possibilities for $f(c)$, we define a positive epsilon. |
| Then there exists a $\delta_1>0$ such that for all $x$, the expression $0 | |
| Then $-\dfrac{f(c)}{2} | |
| But $c$ was the least upper bound of the set $S$ which produced non-positive values of $f(x)$, yet it would appear that we found a smaller upper bound, $c-\delta_1$. This is impossible, and therefore $f(c)>0$ is impossible. | Having arrived at a contradiction, we are forced to reject our most recent supposition. |
| So suppose $f(c) | |
| But $c$ was the least upper bound of the set $S$ which produced non-positive values of $f(x)$, yet it would appear that we found a larger value, $c+\delta_2$, in set $S$. This is impossible, and therefore $f(c) | |
| Therefore, $f(c)=0$. This proves the first case. | Of the three possibilities for $f(c)$, this is the only possibility remaining. But this was with the assumption that $f(a) |
| For the second case, suppose that $f(a)>0$ and $f(b) | The continuity and the values of the function $g(x)$ follow immediately from the continuity and values of $f(x)$. |
| Therefore, by the first (already proven) case, there exists a number $c$ in the interval $[a,b]$ for which $g(c)=0$. | Rather than repeat the entire explanation with the signs of $f(a)$ and $f(b)$ reversed, we use the fact that $g(x)$ meets the conditions already proven in the first case of this theorem, so the result follows for $g(x)$. |
| Therefore, $f(c)=-g(c)=0$. This proves the second of the two cases, hence the theorem is proven. | And then the result for $f(x)$ is immediately available. |
Proof of the Intermediate Value Theorem
Having established Bolzano's Theorem, the Intermediate Value Theorem is a fairly straightforward corollary. First, we shall restate the theorem.
| Define $g(x)=f(x)-L$. Then the function $g(x)$ is continuous on the closed interval $[a,b]$, | The continuity of $g(x)$ is assured by the Difference Limit Law. |
| and $g(a)$ and $g(b)$ will have opposite signs. | Here, we needed to know that $L$ was not equal to either $f(a)$ or $f(b)$, so that neither $g(a)$ nor $g(b)$ would be zero. |
| Then, by Bolzano's Theorem, there exists a number $c$ in the interval $[a,b]$ for which $g(c)=0$. | Since $g(x)$ has met all of the hypotheses of Bolzano's Theorem, the conclusion follows. |
| Thus, $f(c)-L=0$, and therefore $f(c)=L$. | This results from the definition of $g(x)$. |
The Intermediate Value Theorem and Implicit Assumptions
- First Online: 24 September 2021
Cite this chapter

- Nicholas H. Wasserman 6 ,
- Timothy Fukawa-Connelly 7 ,
- Keith Weber 8 ,
- Juan Pablo Mejia-Ramos 8 &
- Stephen Abbott 9
Part of the book series: Springer Texts in Education ((SPTE))
570 Accesses
This chapter engages with the content and proof of the Intermediate Value Theorem; similar to Abbott’s (Understanding analysis (2nd ed.). New York, NY: Springer (2015)) Section 4.5. Using this theorem as a case study, we explore the different ways explicit and implicit assumptions play a role in the back and forth communications between teachers and students in the classroom.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Get 10 units per month
- Download Article/Chapter or Ebook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Similar content being viewed by others
Logical expressivism, logical theory and the critique of inferences.

Introduction
The nash solution is more utilitarian than egalitarian.
Tall and Vinner [ 5 ] make a similar differentiation. They contrast a concept definition , by which they mean a formal definition, with a concept image , by which they mean all the other interesting things associated with that concept.
Brown and Walter [ 3 ] describe this as the “what-if-not” strategy for problem posing.
Ball and Bass [ 2 ] describe this notion of unpacking; teachers need to be able to “deconstruct [their] own mathematical knowledge into less polished and final form, where elemental components are accessible and visible” (p. 98).
Abbott, S. (2015). Understanding analysis (2nd ed.). New York, NY: Springer.
Book Google Scholar
Ball, D. L., & Bass, H. (2000). Interweaving content and pedagogy in teaching and learning to teach: Knowing and using mathematics. In J. Boaler (Ed.), Multiple perspectives on mathematics teaching and learning (pp. 83–104). Westport, CT: Ablex.
Google Scholar
Brown, S. I., & Walter, M. I. (2005). The art of problem posing (3rd ed.). Mahwah, NJ: Lawrence Erlbaum.
Jakobsen, A., Thames, M. H., Ribeiro, C. M., & Delaney, S. (2012). Using practice to define and distinguish horizon content knowledge. In Proceedings of the 12th International Congress on Mathematical Education (pp. 4635–4644). Seoul, South Korea: International Commission on Mathematical Instruction.
Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics , 12 (2), 151–169.
Article Google Scholar
Download references
Author information
Authors and affiliations.
Teachers College, Columbia University, New York, NY, USA
Nicholas H. Wasserman
Temple University, Philadelphia, PA, USA
Timothy Fukawa-Connelly
Graduate School of Education, Rutgers University, New Brunswick, NJ, USA
Keith Weber & Juan Pablo Mejia-Ramos
Department of Mathematics, Middlebury College, Middlebury, VT, USA
Stephen Abbott
You can also search for this author in PubMed Google Scholar
Rights and permissions
Reprints and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Wasserman, N.H., Fukawa-Connelly, T., Weber, K., Pablo Mejia-Ramos, J., Abbott, S. (2022). The Intermediate Value Theorem and Implicit Assumptions. In: Understanding Analysis and its Connections to Secondary Mathematics Teaching. Springer Texts in Education. Springer, Cham. https://doi.org/10.1007/978-3-030-89198-5_7
Download citation
DOI : https://doi.org/10.1007/978-3-030-89198-5_7
Published : 24 September 2021
Publisher Name : Springer, Cham
Print ISBN : 978-3-030-89197-8
Online ISBN : 978-3-030-89198-5
eBook Packages : Education Education (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
- Skip to navigation (Press Enter)
- Skip to main content (Press Enter)
Math Insight
Intermediate value theorem, location of roots.
The assertion of the Intermediate Value Theorem is something which is probably ‘intuitively obvious’, and is also provably true : if a function $f$ is continuous on an interval $[a,b]$ and if $f(a) 0$ (or vice-versa), then there is some third point $c$ with $a interval bisection , for a reason we'll see below. We will not pursue this method very far, because there are better methods to use once we have invoked this just to get going.
For example, we probably don't know a formula to solve the cubic equation $$x^3-x+1=0$$ But the function $f(x)=x^3-x+1$ is certainly continuous, so we can invoke the Intermediate Value Theorem as much as we'd like. For example, $f(2)=7 > 0$ and $f(-2)=-5 midpoint , bisecting the interval $[-2,2]$: we have $f(0)=1 > 0$. Therefore, since $f(-2)=-5 0$ and $f(2) > 0$, we can't say anything at this point about whether or not there are roots in $[0,2]$. Again bisecting the interval $[-2,0]$ where we know there is a root, we compute $f(-1)=1 > 0$. Thus, since $f(-2) < 0$, we know that there is a root in $[-2,-1]$ (and have no information about $[-1,0]$).
If we continue with this method, we can obtain as good an approximation as we want! But there are faster ways to get a really good approximation, as we'll see.
Unless a person has an amazing intuition for polynomials (or whatever), there is really no way to anticipate what guess is better than any other in getting started.
Invoke the Intermediate Value Theorem to find an interval of length $1$ or less in which there is a root of $x^3+x+3 =0$: Let $f(x)=x^3+x+3$. Just, guessing, we compute $f(0)=3 > 0$. Realizing that the $x^3$ term probably ‘dominates’ $f$ when $x$ is large positive or large negative, and since we want to find a point where $f$ is negative, our next guess will be a ‘large’ negative number: how about $-1$? Well, $f(-1)=1 > 0$, so evidently $-1$ is not negative enough. How about $-2$? Well, $f(-2)=-7 0$. Then, invoking the Intermediate Value Theorem, there is a root in the interval $[-2,-1]$.
Of course, typically polynomials have several roots, but the number of roots of a polynomial is never more than its degree . We can use the Intermediate Value Theorem to get an idea where all of them are.
Invoke the Intermediate Value Theorem to find three different intervals of length $1$ or less in each of which there is a root of $x^3-4x+1=0$: first, just starting anywhere, $f(0)=1 > 0$. Next, $f(1)=-2 0$ and $f(1) 0$. So, with some luck here, since $f(1) 0$, by the Intermediate Value Theorem there is a root in $[1,2]$. Now if we somehow imagine that there is a negative root as well, then we try $-1$: $f(-1)=4 > 0$. So we know nothing about roots in $[-1,0]$. But continue: $f(-2)=1 > 0$, and still no new conclusion. Continue: $f(-3)=-14 0$, by the Intermediate Value Theorem there is a third root in the interval $[-3,-2]$.
Notice how even the ‘bad’ guesses were not entirely wasted.
Thread navigation
Calculus refresher.
- Previous: Related rates
- Next: Newton's Method
Similar pages
- The idea of the derivative of a function
- Derivatives of polynomials
- Derivatives of more general power functions
- A refresher on the quotient rule
- A refresher on the product rule
- A refresher on the chain rule
- Related rates
- Newton's Method
- Derivatives of transcendental functions
- L'Hospital's rule
- More similar pages
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Hypotheses on the Intermediate Value Theorem
Background A typical statement of the Intermediate Value Theorem given in elementary analysis, this particular one lifted from Wikipedia , goes as follows:
If $f$ is a real-valued continuous function on the interval $[a,b]$ and $u$ is a number between $f(a)$ and $f(b)$ then there exists a number $c \in [a,b]$ such that f(c) = u
This statement would lead one to believe that the result is somehow related to the compactness of $[a,b]$. However, it is a theorem of general topology that if $f$ is a real-valued continuous function defined on a connected space $X$ then it takes on every value between $f(p)$ and $f(q)$ for every $p,q \in X$. Even more generally, we have that since continuous maps preserve connectivity, $g(X)$ is connected for any continuous map $g$ defined on $X$ to some other topological space $Y$.
In fact, the first more specialized version follows almost immediately from the topological version, taking into account the fact that a subset of $\mathbb{R}$ is connected if and only if it is an interval.
Question Is there a reason why we cannot state the first theorem more generally as:
If $f$ is a real-valued continuous function on an interval $J \subset \mathbb{R}$, $a,b \in J$ and $u$ is a number between $f(a)$ and $f(b)$ then there exists a number $c \in J$ such that f(c) = u
- real-analysis
- 2 $\begingroup$ Well, you want $a$ and $b$ in the interval. $\endgroup$ – Mark Commented Feb 14, 2012 at 21:26
- $\begingroup$ no there is a problem you can see Introduction to real analysis by Bartle page 133 $\endgroup$ – user24993 Commented Feb 14, 2012 at 21:37
- 2 $\begingroup$ And when $a$ and $b$ are in the interval, you can restrict your attention to the closed interval having those two as end points, and so you're back to the original formulation. $\endgroup$ – Harald Hanche-Olsen Commented Feb 14, 2012 at 21:45
- $\begingroup$ Ok, I see; so, the point is both $a$ and $b$ must be in the interval to begin with (which, of course makes sense) and therefore one might as well consider the (closed) interval $[a,b]$ (as opposed to some open interval $(a_0, b_0)$ where $a_0 \leq a < b \leq b_0$ $\endgroup$ – ItsNotObvious Commented Feb 14, 2012 at 22:07
- $\begingroup$ @3Sphere: Indeed. $\endgroup$ – Mark Commented Feb 14, 2012 at 23:23
Take $f(x) =x$ for $x\in(0,1]$ and $f(0) =-1$. Then $f$ is continuous on $J = (0,1)$ in the subspace topology, but for $u = -0.5$ there is no $c$ such that $f(c) = u$.
- $\begingroup$ I suspect that this answer is based on weaker hypotheses thant the questioner intended. $\endgroup$ – Harald Hanche-Olsen Commented Feb 14, 2012 at 21:46
- $\begingroup$ @HaraldHanche-Olsen: I didn't say that the definition OP has in mind is incorrect (by the way, there was no "$a,b\in J$" part when I've answered). I just pointed out the possible problem related to this definition since it was unclear if $a,b\in J$ or not. $\endgroup$ – SBF Commented Feb 15, 2012 at 8:52
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged real-analysis ..
- Featured on Meta
- Upcoming sign-up experiments related to tags
Hot Network Questions
- Do IDE data lines need pull-up resistors?
- Why is completeness (as in Gödel completeness theorem) a desirable feature?
- How to Control StringContainsQ
- How many different kinds of fairy units?
- Have there been any scholarly attempts and/or consensus as regards the missing lines of "The Ruin"?
- Why did Geordi have his visor replaced with ocular implants between Generations and First Contact?
- If the slope of a secant is always irrational, is the function linear?
- Am I doing a forcing argument here?
- Simple Container Class
- How do I get my D&D group to engage to a minimum
- Why only Balmer series of hydrogen spectrum is visible?
- How are "pursed" and "rounded" synonymous?
- What is this weapon used in The Peacemaker?
- What kind of sequence is between an arithmetic and geometric sequence?
- "All due respect to jazz." - Does this mean the speaker likes it or dislikes it?
- Why can't I conserve mass instead of moles and apply ratio in this problem?
- How to make a 3D ripple effect like the one shown?
- Can a planet have a warm, tropical climate both at the poles and at the equator?
- Entering the US with a hotel reservation booked under my brother's name
- Eye Floaters Optics
- How exactly does a seashell make the humming sound?
- Diagnosing tripped breaker on the dishwasher circuit?
- Are both vocal cord and vocal chord correct?
- Output the Steiner system S(5,8,24)
You are about to erase your work on this activity. Are you sure you want to do this?
Updated Version Available
There is an updated version of this activity. If you update to the most recent version of this activity, then your current progress on this activity will be erased. Regardless, your record of completion will remain. How would you like to proceed?
Mathematical Expression Editor
Here we see a consequence of a function being continuous.
Now, let’s contrast this with a time when the conclusion of the Intermediate Value Theorem does not hold.
Building on the question above, it is not difficult to see that each of the hypothesis of the Intermediate Value Theorem are necessary.
Let’s see the Intermediate Value Theorem in action.
This example also points the way to a simple method for approximating roots.
Now we move on to a more subtle example:
- They start and finish drinking at the same times.
- Roxy starts with more water than Yuri, and leaves less water left in her bowl than Yuri.
And finally, an example when the Intermediate Value Theorem does not apply.
- They start and finish eating at the same times.
- Roxy starts with more food than Yuri, and leaves less food uneaten than Yuri.

IMAGES
VIDEO
COMMENTS
The intermediate value theorem describes a key property of continuous functions: for any function f that's continuous over the interval [ a, b] , the function will take any value between f ( a) and f ( b) over the interval. More formally, it means that for any value L between f ( a) and f ( b) , there's a value c in [ a, b] for which f ( c) = L .
This page titled 7.2: Proof of the Intermediate Value Theorem is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Eugene Boman and Robert Rogers via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.
The intermediate value theorem is used to verify the existence of an equation's root in a given interval, which shows whether the given function has its zero (or f (x) = 0) within the interval (a, b). Let us verify this statement using the function f (x) = x 4 - 2x 3 + 3x - 21, which has a zero within the interval [1, 3]
Intermediate Value Theorem. The idea behind the Intermediate Value Theorem is this: When we have two points connected by a continuous curve: one point below the line. the other point above the line. then there is at least one place where the curve crosses the line! Well of course we must cross the line to get from A to B!
Transcript. Discover the Intermediate Value Theorem, a fundamental concept in calculus that states if a function is continuous over a closed interval [a, b], it encompasses every value between f (a) and f (b) within that range. Dive into this foundational theorem and explore its connection to continuous functions and their behavior on intervals.
The intermediate value theorem states that if a continuous function attains two values, it must also attain all values in between these two values. Intuitively, a continuous function is a function whose graph can be drawn "without lifting pencil from paper." For instance, if f (x) f (x) is a continuous function that connects the points [0,0] [0 ...
Remembering that f(x1) ≥ k f ( x 1) ≥ k we have. k − ϵ < f(c) (2) (2) k − ϵ < f ( c) Then combining (1) ( 1) and (2) ( 2), we have. k − ϵ < f(c) < k + ϵ k − ϵ < f ( c) < k + ϵ. However, the only way this holds for any ϵ > 0 ϵ > 0, is for f(c) = k f ( c) = k. QED.
The intermediate value theorem says that every continuous function is a Darboux function. However, not every Darboux function is continuous; i.e., the converse of the intermediate value theorem is false. As an example, take the function f : [0, ∞) → [−1, 1] defined by f(x) = sin (1/x) for x > 0 and f(0) = 0. This function is not ...
The conclusions may be obvious when you understand the statements and look at a graph, but they are powerful nonetheless. ... The Intermediate and Extreme Value Theorems. The Intermediate Value Theorem states that if a function is continuous on a closed interval and u is a value ... The converse of an if then statement is a new statement with ...
so by the Intermediate Value Theorem, f has a root between 0.61 and 0.62, and the root is 0.6 rounded to one decimal place. The Intermediate Value Theorem can be use to show that curves cross: Explain why the functions. f(x) g(x) =x2 x−−√3 = 2(x + 1) cos( x−−√3) intersect on the interval [0,(π 2)3] . To start, note that both f and ...
Informally, a set S ⊂ Rn S ⊂ R n is path-connected if any two points in S S can be connected by a path that stays in S S. More precisely: Definition. A set S ⊂Rn S ⊂ R n is path-connected if, for every pair of points x x and y y in S S, ∃ continuous γ: [0, 1] → S, such that γ(0) =x, γ(1) = y. (1) (1) ∃ continuous γ: [ 0, 1 ...
Bolzano's Intermediate Value Theorem last updated 1jul13 formerly 26apr11, 23apr12 \begin{document} \maketitle \section{Introduction} In 1817 Bernhard Bolzano published a very modern proof of the \textit{ Intermediate Value Theorem} (IVT) for continuous functions. Unfortunately, he was obliged to publish in an obscure Bohemian journal.
An intermediate value theorem, if c = 0, then it is referred to as Bolzano's theorem. Intermediate Theorem Proof. We are going to prove the first case of the first statement of the intermediate value theorem since the proof of the second one is similar. We will prove this theorem by the use of completeness property of real numbers. The proof ...
The intermediate value theorem (also known as IVT or IVT theorem) says that if a function f(x) is continuous on an interval [a, b], then for every y-value between f(a) and f(b), there exists some x-value in the interval (a, b). i.e., if f(x) is continuous on [a, b], then it should take every value that lies between f(a) and f(b). Recall that a continuous function is a function whose graph is a ...
The Intermediate Value Theorem. We already know from the definition of continuity at a point that the graph of a function will not have a hole at any point where it is continuous. The Intermediate Value Theorem basically says that the graph of a continuous function on a closed interval will have no holes on that interval.
The Intermediate Value Theorem (IVT) is a statement about continuous functions; namely, that if a function f is continuous on [a, b], then on that interval the function will attain all values between f(a) and f(b). Abbott also defines what he calls the Intermediate Value Property (IVP), in Definition 4.5.3 [1, p. 139].
First, the function f ( x) = x 3 is continuous on the interval [ 2, 3] since is a polynomial. Second, observe that f ( 2) = 2 3 = 8, and f ( 3) = 3 3 = 27, so that 10 is an intermediate value, i.e., f ( 2) < 10 < f ( 3). Now we can apply the Intermediate Value Theorem to conclude that the equation x 3 = 10 has a least one solution between x = 2 ...
Intermediate Value Theorem If f f is a continuous function for all x x in the closed interval [a, b] [ a, b] and d d is between f(a) f ( a) and f(b) f ( b), then there is a number c c in [a, b] [ a, b] such that f(c) = d f ( c) = d . Now, let's contrast this with a time when the conclusion of the Intermediate Value Theorem does not hold.
Example 2. Invoke the Intermediate Value Theorem to find an interval of length 1 1 or less in which there is a root of x3 + x + 3 = 0 x 3 + x + 3 = 0: Let f(x) = x3 + x + 3 f ( x) = x 3 + x + 3. Just, guessing, we compute f(0) = 3 > 0 f ( 0) = 3 > 0. Realizing that the x3 x 3 term probably 'dominates' f f when x x is large positive or large ...
Background A typical statement of the Intermediate Value Theorem given in elementary analysis, this particular one lifted from Wikipedia, goes as follows: If f f is a real-valued continuous function on the interval [a, b] [ a, b] and u u is a number between f(a) f ( a) and f(b) f ( b) then there exists a number c ∈ [a, b] c ∈ [ a, b] such ...
Repeating the process x f ( x) 0.61 − 0.046719 0.62 0.011528 and using the Intermediate Value Theorem, we can conclude that f has a root between 0.61 and 0.62, and the root is 0.6 rounded to one decimal place. The Intermediate Value Theorem can be used to show that curves cross: Explain why the graphs of the functions f ( x) = x 2 ln. .
The conclusions may be obvious when you understand the statements and look at a graph, but they are powerful nonetheless. ... The Intermediate Value Theorem states that if a function is continuous on a closed interval and @$\\begin ... The converse of an if then statement is a new statement with the hypothesis of the original statement switched ...
Intermediate Value Theorem If f f is a continuous function for all x x in the closed interval [a, b] [ a, b] and d d is between f(a) f ( a) and f(b) f ( b), then there is a number c c in [a, b] [ a, b] such that f(c) = d f ( c) = d . Now, let's contrast this with a time when the conclusion of the Intermediate Value Theorem does not hold.