graphical representation of a quadratic polynomial

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 5: Polynomial graphs

About this unit.

In this unit, we will use everything that we know about polynomials in order to analyze their graphical behavior. Specifically, we will find polynomials' zeros (i.e., x-intercepts) and analyze how they behave as the x-values become infinitely positive or infinitely negative (i.e., end-behavior).

Zeros of polynomials

• Zeros of polynomials introduction (Opens a modal)
• Zeros of polynomials: plotting zeros (Opens a modal)
• Zeros of polynomials: matching equation to zeros (Opens a modal)
• Zeros of polynomials: matching equation to graph (Opens a modal)
• Zeros of polynomials (with factoring): grouping (Opens a modal)
• Zeros of polynomials (with factoring): common factor (Opens a modal)
• Zeros of polynomials (factored form) Get 3 of 4 questions to level up!
• Zeros of polynomials (with factoring) Get 3 of 4 questions to level up!

Positive and negative intervals of polynomials

• Positive and negative intervals of polynomials (Opens a modal)
• Multiplicity of zeros of polynomials (Opens a modal)
• Zeros of polynomials (multiplicity) (Opens a modal)
• Zeros of polynomials & their graphs (Opens a modal)
• Positive & negative intervals of polynomials (Opens a modal)
• Positive & negative intervals of polynomials Get 3 of 4 questions to level up!
• Zeros of polynomials (multiplicity) Get 3 of 4 questions to level up!

End behavior of polynomials

• Intro to end behavior of polynomials (Opens a modal)
• End behavior of polynomials (Opens a modal)
• End behavior of polynomials Get 3 of 4 questions to level up!

Putting it all together

• Graphs of polynomials (Opens a modal)
• Graphs of polynomials: Challenge problems (Opens a modal)
• Polynomial graphs: FAQ (Opens a modal)

CBSE Papers, Questions, Answers, MCQ ...

Blog provides NCERT solutions, CBSE, NTSE, Olympiad study material, model test papers, important Questions and Answers asked in CBSE examinations. References to Educational Sites and resources.

• CareerAfter12
• Syllabus 2017-18
• Entrance Exams

Monday 21 June 2021

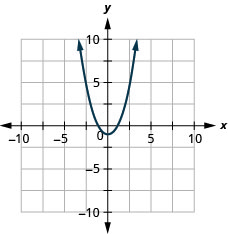
Cbse class 10 maths lab activity - draw quadratic polynomial and observe (#class10maths)(#class10mathsactivity), cbse class 10 maths lab activity - draw quadratic polynomial and observe.

OBJECTIVE : To draw the graph of a quadratic polynomial and observe.

(i) The shape of the curve when the coefficient of x² is positive.

(ii) The shape of the curve when the coefficient of x² is negative.

(iii) Its number of zeroes.

MATERIAL REQUIRED

Cardboard, graph paper, ruler, pencil, eraser, pen, adhesive.

STEPS OF CONSTRUCTION

1. Take cardboard of a convenient size and paste a graph paper on it. 

2. Consider a quadratic polynomial f(x) = ax² + bx + c

3. Two cases arise:

(i) a > 0 (ii) a < 0

4. Find the ordered pairs (x, f (x)) for different values of x.

5. Plot these ordered pairs in the cartesian plane

6. Join the plotted points by a free hand curve. Based on polynomial used, you may have graphs as shown in following figures:

DEMONSTRATION

1. The shape of the curve obtained in each case is a parabola.

2. Parabola opens upward when coefficient of x² is positive.

3. It opens downward when coefficient of x² is negative. 

4. Maximum number of zeroes which a quadratic polynomial can have is 2.

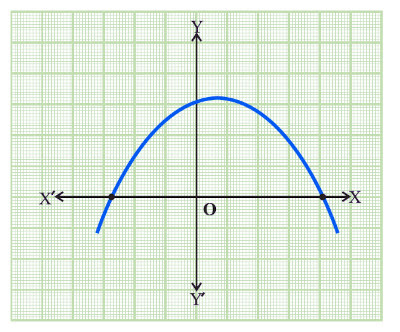
OBSERVATION

1. Parabola in Fig. 1 opens ______

2. Parabola in Fig. 2 opens _______

3. In Fig. 1, parabola intersects x-axis at ______ point(s).

4. Number of zeroes of the given polynomial is ________.

5. Parabola in Fig. 2 intersects x-axis at ______ point(s).

6. Number of zeroes of the given polynomial is ______.

7. Parabola in Fig.3 intersects x-axis at ______ point(s).

8. Number of zeroes of the given polynomial is _______.

9. Maximum number of zeroes which a quadratic polynomial can have is __________.

APPLICATION

This activity helps in:

1. understanding the geometrical representation of a quadratic polynomial

2. finding the number of zeroes of a quadratic polynomial

A Sample project is shown here.

No comments:

Post a comment.

We love to hear your thoughts about this post!

Note: only a member of this blog may post a comment.

Ad-Blocker Detected!

Please turn off the ad blocker. This is only way that we can earn some penny. Please support us by trun off the ad blocker. Thank you!!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.6: Graph Quadratic Functions Using Properties

• Last updated
• Save as PDF
• Page ID 108360

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Recognize the graph of a quadratic function
• Find the axis of symmetry and vertex of a parabola
• Find the intercepts of a parabola
• Graph quadratic functions using properties
• Solve maximum and minimum applications
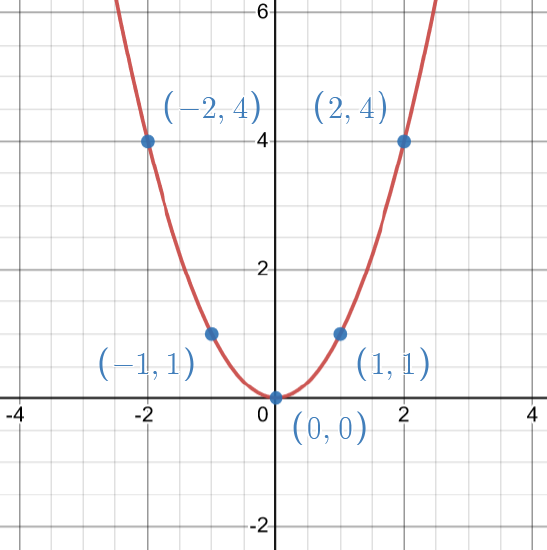
• Graph the function \(f(x)=x^{2}\) by plotting points.
• Solve: \(2 x^{2}+3 x-2=0\).
• Evaluate \(-\frac{b}{2 a}\) when \(a=3\) and \(b=-6\).

• \(x=\frac{1}{2}, x=-2\)

Recognize the Graph of a Quadratic Function

Previously we very briefly looked at the function \(f(x)=x^{2}\), which we called the square function. It was one of the first non-linear functions we looked at. Now we will graph functions of the form \(f(x)=a x^{2}+b x+c\) if \(a \neq 0\). We call this kind of function a quadratic function.

Definition \(\PageIndex{1}\)

A quadratic function , where \(a, b\), and \(c\) are real numbers and \(a≠0\), is a function of the form

\(f(x)=a x^{2}+b x+c\)

We graphed the quadratic function \(f(x)=x^{2}\) by plotting points.

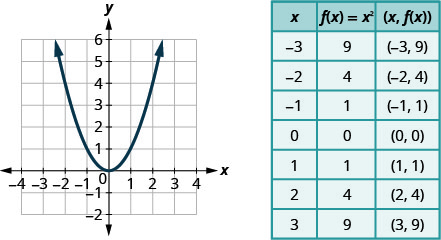
Every quadratic function has a graph that looks like this. We call this figure a parabola . Let’s practice graphing a parabola by plotting a few points.

Example \(\PageIndex{1}\)

Graph: \(f(x)=x^{2}-1\).

We will graph the function by plotting points.

Exercise \(\PageIndex{2}\)

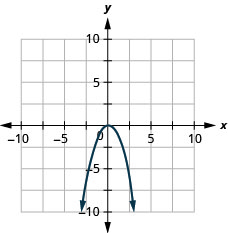
Graph \(f(x)=-x^{2}\).

Exercise \(\PageIndex{3}\)

Graph \(f(x)=x^{2}-1\).

All graphs of quadratic functions of the form \(f(x)=a x^{2}+b x+c\) are parabolas that open upward or downward. See Figure 9.6.6

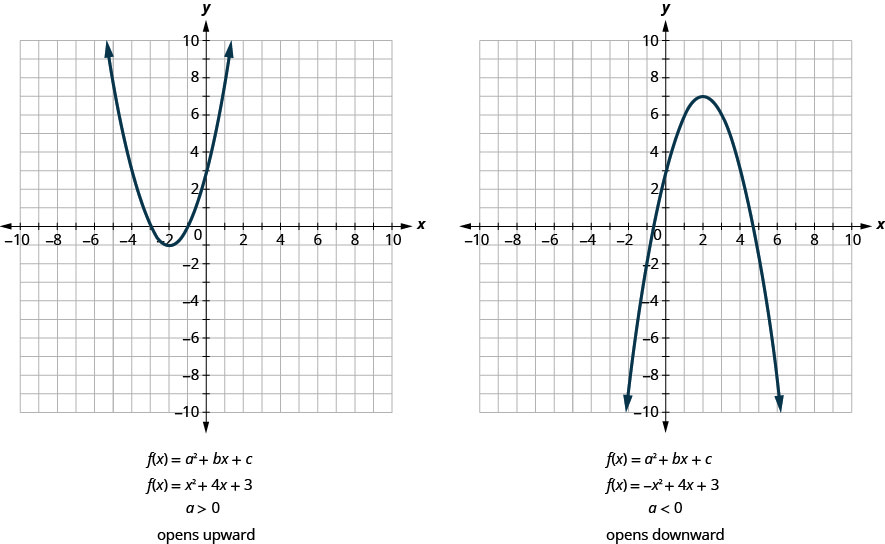
Notice that the only difference in the two functions is the negative sign before the quadratic term (\(x^{2}\) in the equation of the graph in Figure 9.6.6 ). When the quadratic term, is positive, the parabola opens upward, and when the quadratic term is negative, the parabola opens downward.

Definition: PARABOLA

Parabola Orientation

For the graph of the quadratic function \(f(x)=a x^{2}+b x+c\), if

Example \(\PageIndex{4}\)

Determine whether each parabola opens upward or downward:

• \(f(x)=-3 x^{2}+2 x-4\)
• \(f(x)=6 x^{2}+7 x-9\)

a. Find the value of \(a\).

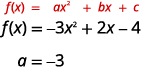
Since the \(a\) is negative, the parabola will open downward.

b. Find the value of \(a\).

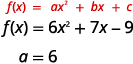
Since the \(a\) is positive, the parabola will open upward.

Exercise \(\PageIndex{4}\)

Determine whether the graph of each function is a parabola that opens upward or downward:

• \(f(x)=2 x^{2}+5 x-2\)
• \(f(x)=-3 x^{2}-4 x+7\)

Exercise \(\PageIndex{5}\)

• \(f(x)=-2 x^{2}-2 x-3\)
• \(f(x)=5 x^{2}-2 x-1\)

Find the Axis of Symmetry and Vertex of a Parabola

Look again at Figure 9.6.10 . Do you see that we could fold each parabola in half and then one side would lie on top of the other? The ‘fold line’ is a line of symmetry. We call it the axis of symmetry of the parabola.

We show the same two graphs again with the axis of symmetry.

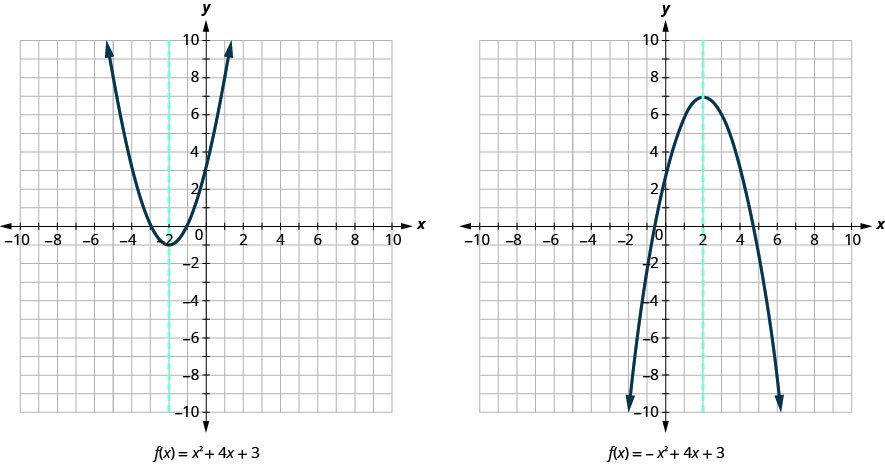
The equation of the axis of symmetry can be derived by using the Quadratic Formula. We will omit the derivation here and proceed directly to using the result. The equation of the axis of symmetry of the graph of \(f(x)=a x^{2}+b x+c\) is \(x=-\frac{b}{2 a}\).

So to find the equation of symmetry of each of the parabolas we graphed above, we will substitute into the formula \(x=-\frac{b}{2 a}\).

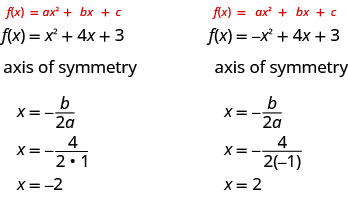
Notice that these are the equations of the dashed blue lines on the graphs.

The point on the parabola that is the lowest (parabola opens up), or the highest (parabola opens down), lies on the axis of symmetry. This point is called the vertex of the parabola.

We can easily find the coordinates of the vertex, because we know it is on the axis of symmetry. This means its \(x\)-coordinate is \(-\frac{b}{2 a}\). To find the \(y\)-coordinate of the vertex we substitute the value of the \(x\)-coordinate into the quadratic function.

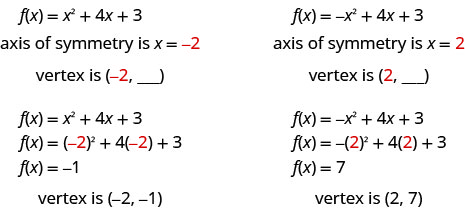
Axis of Symmetry and Vertex of a Parabola

The graph of the function \(f(x)=a x^{2}+b x+c\) is a parabola where:

• the axis of symmetry is the vertical line \(x=-\frac{b}{2 a}\).
• the vertex is a point on the axis of symmetry, so its \(x\)-coordinate is \(-\frac{b}{2 a}\)
• the \(y\)-coordinate of the vertex is found by substituting \(x=-\frac{b}{2 a}\) into the quadratic equation.

Example \(\PageIndex{6}\)

For the graph of \(f(x)=3 x^{2}-6 x+2\) find:

• the axis of symmetry

Exercise \(\PageIndex{7}\)

For the graph of \(f(x)=2 x^{2}-8 x+1\) find:

Exercise \(\PageIndex{8}\)

For the graph of \(f(x)=2 x^{2}-4 x-3\) find:

Find the Intercepts of a Parabola

When we graphed linear equations, we often used the \(x\)- and \(y\)-intercepts to help us graph the lines. Finding the coordinates of the intercepts will help us to graph parabolas, too.

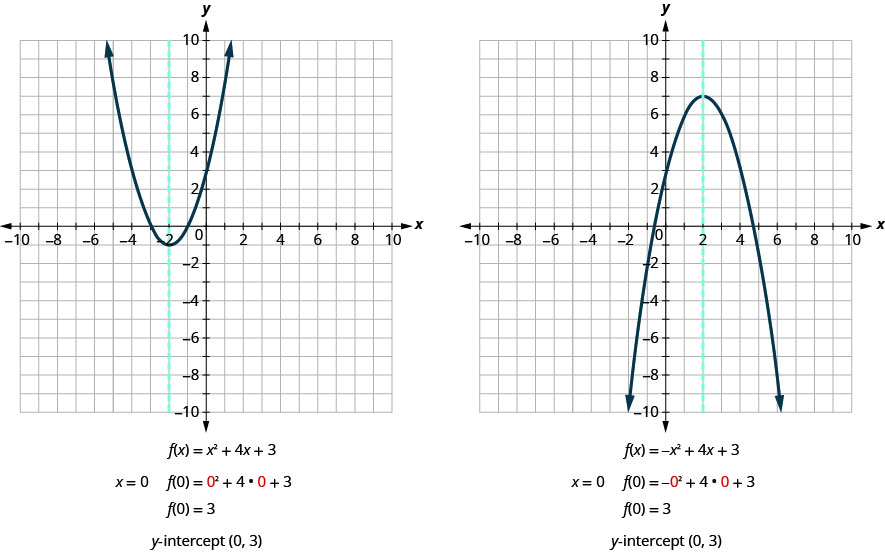
Remember, at the \(y\)-intercept the value of \(x\) is zero. So to find the \(y\)-intercept, we substitute \(x=0\) into the function.

Let’s find the \(y\)-intercepts of the two parabolas shown in Figure 9.6.20 .

An \(x\)-intercept results when the value of \(f(x)\) is zero. To find an \(x\)-intercept, we let \(f(x)=0\). In other words, we will need to solve the equation \(0=a x^{2}+b x+c\) for \(x\).

\(\begin{aligned} f(x) &=a x^{2}+b x+c \\ 0 &=a x^{2}+b x+c \end{aligned}\)

Solving quadratic equations like this is exactly what we have done earlier in this chapter!

We can now find the \(x\)-intercepts of the two parabolas we looked at. First we will find the \(x\)-intercepts of the parabola whose function is \(f(x)=x^{2}+4 x+3\).

Now we will find the \(x\)-intercepts of the parabola whose function is \(f(x)=-x^{2}+4 x+3\).

We will use the decimal approximations of the \(x\)-intercepts, so that we can locate these points on the graph,

\((2+\sqrt{7}, 0) \approx(4.6,0) \quad(2-\sqrt{7}, 0) \approx(-0.6,0)\)

Do these results agree with our graphs? See Figure 9.6.34

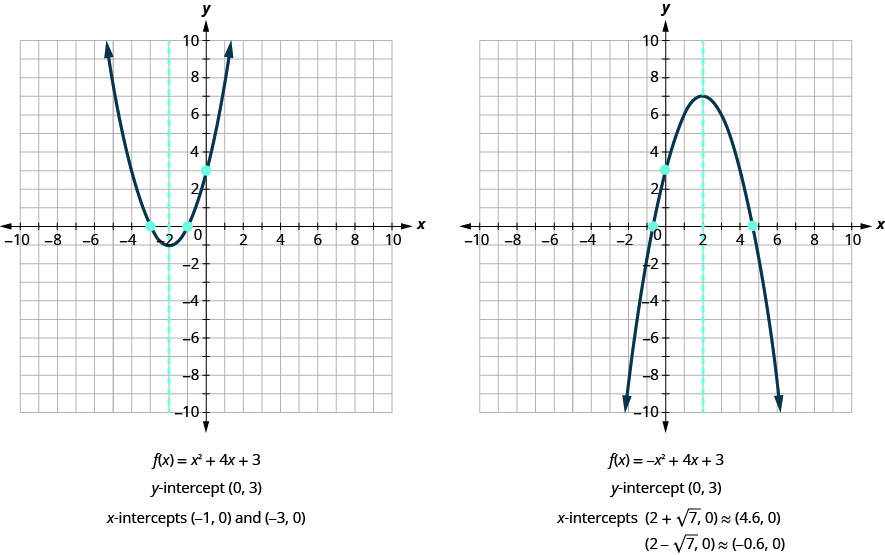
To find the intercepts of a parabola whose function is \(f(x)=a x^{2}+b x+c\):

\(y\)-intercept

• Let \(x=0\) and solve for \(f(x)\).

\(x\)-intercepts

Let \(f(x)=0\) and solve for \(x\)

Example \(\PageIndex{8}\)

Find the intercepts of the parabola whose function is \(f(x)=x^{2}-2 x-8\).

Exercise \(\PageIndex{9}\)

Find the intercepts of the parabola whose function is \(f(x)=x^{2}+2 x-8\).

\(y\) -intercept: \((0,-8) x\) -intercepts \((-4,0),(2,0)\)

Exercise \(\PageIndex{10}\)

Find the intercepts of the parabola whose function is \(f(x)=x^{2}-4 x-12\).

\(y\) -intercept: \((0,-12) x\) -intercepts \((-2,0),(6,0)\)

In this chapter, we have been solving quadratic equations of the form \(a x^{2}+b x+c=0\). We solved for \(x\) and the results were the solutions to the equation.

We are now looking at quadratic functions of the form \(f(x)=a x^{2}+b x+c\). The graphs of these functions are parabolas. The \(x\) - intercepts of the parabolas occur where \(f(x)=0\).

For example:

Quadratic equation

\(\begin{aligned}x^{2}-2 x-15 & =0\quad \text{Let}\:f(x)=0 \\ (x-5)(x+3) &=0 \\ x-5=0\:\:x+3 & =0 \\ x=5\:\:\:x&=-3\end{aligned}\)

Quadratic function

\(\begin{aligned} f(x) &=x^{2}-2 x-15 \\ 0 &=x^{2}-2 x-15 \\ 0 &=(x-5)(x+3) \\ x-5 &=0 \quad x+3=0 \\ x &=5 \quad x=-3 \\(5,0) & \text { and }(-3,0) \\& x\text { -intercepts } \end{aligned}\)

The solutions of the quadratic function are the \(x\) values of the \(x\) - intercepts.

Earlier, we saw that quadratic equations have \(2, 1\), or \(0\) solutions. The graphs below show examples of parabolas for these three cases. Since the solutions of the functions give the \(x\)-intercepts of the graphs, the number of \(x\)-intercepts is the same as the number of solutions.

Previously, we used the discriminant to determine the number of solutions of a quadratic function of the form \(a x^{2}+b x+c=0\). Now we can use the discriminant to tell us how many \(x\)-intercepts there are on the graph.

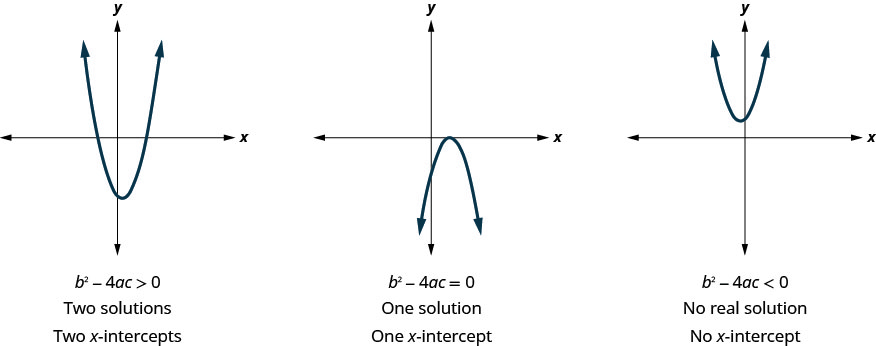
Before you to find the values of the \(x\)-intercepts, you may want to evaluate the discriminant so you know how many solutions to expect.

Example \(\PageIndex{11}\)

Find the intercepts of the parabola for the function \(f(x)=5 x^{2}+x+4\).

Exercise \(\PageIndex{12}\)

Find the intercepts of the parabola whose function is \(f(x)=3 x^{2}+4 x+4\).

\(y\)-intercept: \((0,4)\) no \(x\)-intercept

Exercise \(\PageIndex{13}\)

Find the intercepts of the parabola whose function is \(f(x)=x^{2}-4 x-5\)

\(y\)-intercept: \((0,-5)\) \(x\)-intercepts \((-1,0),(5,0)\)

Graph Quadratic Functions Using Properties

Now we have all the pieces we need in order to graph a quadratic function. We just need to put them together. In the next example we will see how to do this.

Example \(\PageIndex{14}\)

Graph \(f(x)=x^{2}-6x+8\) by using its properties.

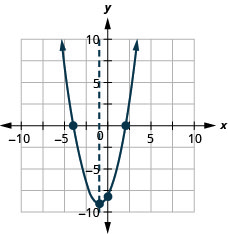
Exercise \(\PageIndex{15}\)

Graph \(f(x)=x^{2}+2x-8\) by using its properties.

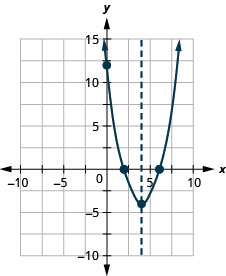
Exercise \(\PageIndex{16}\)

Graph \(f(x)=x^{2}-8x+12\) by using its properties.

We list the steps to take in order to graph a quadratic function here.

To Graph a Quadratic Function Using Properties

• Determine whether the parabola opens upward or downward.
• Find the equation of the axis of symmetry.
• Find the vertex.
• Find the \(y\)-intercept. Find the point symmetric to the \(y\)-intercept across the axis of symmetry.
• Find the \(x\)-intercepts. Find additional points if needed.
• Graph the parabola.

We were able to find the \(x\)-intercepts in the last example by factoring. We find the \(x\)-intercepts in the next example by factoring, too.

Example \(\PageIndex{17}\)

Graph \(f(x)=-x^{2}+6 x-9\) by using its properties.

Exercise \(\PageIndex{18}\)

Graph \(f(x)=3 x^{2}+12 x-12\) by using its properties.

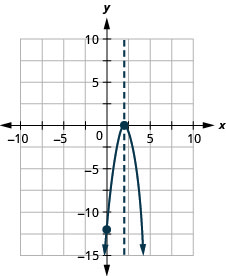
Exercise \(\PageIndex{19}\)

Graph \(f(x)=4 x^{2}+24 x+36\) by using its properties.

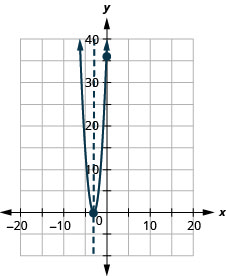
For the graph of \(f(x)=-x^{2}+6 x-9\), the vertex and the \(x\)-intercept were the same point. Remember how the discriminant determines the number of solutions of a quadratic equation? The discriminant of the equation \(0=-x^{2}+6x-9\) is \(0\), so there is only one solution. That means there is only one \(x\)-intercept, and it is the vertex of the parabola.

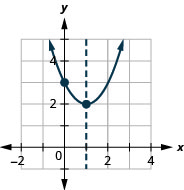
How many \(x\)-intercepts would you expect to see on the graph of \(f(x)=x^{2}+4 x+5\)?

Example \(\PageIndex{20}\)

Graph \(f(x)=x^{2}+4 x+5\) by using its properties.

Exercise \(\PageIndex{21}\)

Graph \(f(x)=x^{2}-2 x+3\) by using its properties.

Exercise \(\PageIndex{22}\)

Graph \(f(x)=-3x^{2}-6 x-4\) by using its properties.

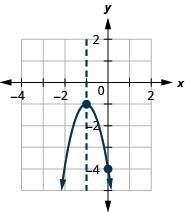
Finding the \(y\)-intercept by finding \(f(0)\) is easy, isn't it? Sometimes we need to use the Quadratic Formula to find the \(x\)-intercepts.

Example \(\PageIndex{23}\)

Graph \(f(x)=2 x^{2}-4 x-3\) by using its properties.

Exercise \(\PageIndex{24}\)

Graph \(f(x)=5 x^{2}+10 x+3\) by using its properties.

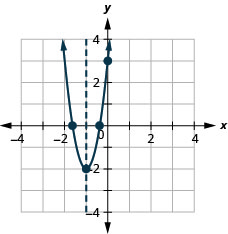
Exercise \(\PageIndex{25}\)

Graph \(f(x)=-3 x^{2}-6 x+5\) by using its properties.

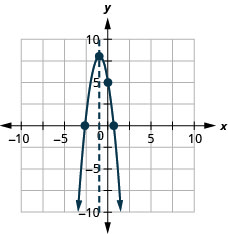
Key Concepts

• \(a>0\), the parabola opens upward.
• \(a<0\), the parabola opens downward.
• the vertex is a point on the axis of symmetry, so its \(x\)-coordinate is \(-\frac{b}{2 a}\).
• Let \(f (x)= 0\) and solve for \(x\).
• Find the \(y\)-intercept. Find the point symmetric to the y -intercept across the axis of symmetry.

• Geometrical Representation of Zeroes of a Polynomial

In the study of polynomials , you are aware that a real number ‘k’ is a zero of the polynomial p(x) if p(k) = 0. Remember, zero of a polynomial is different from a zero polynomial. We have seen the Remainder theorem use the concept of zeroes of a polynomial too. In order to understand their importance, we will look at the geometrical representations of linear and quadratic polynomials and the geometrical meaning of their zeroes.

Suggested Videos

Linear polynomial.

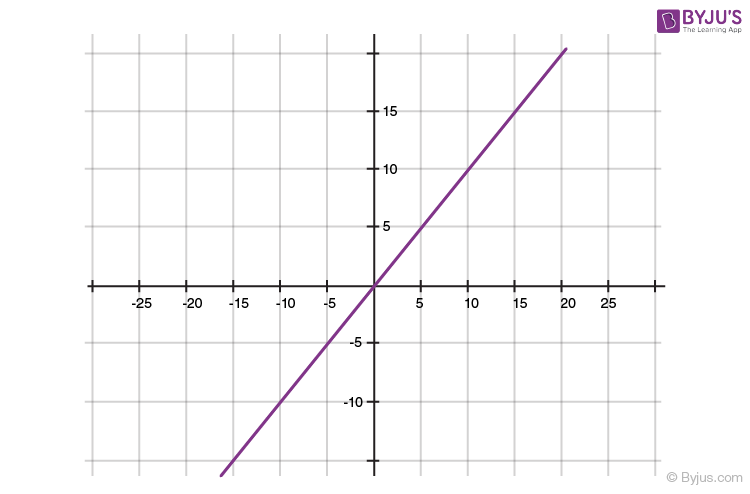
Let’s look at a linear polynomial ax + b, where a ≠ 0. You have already studied that the graph of y = ax + b is a straight line . Let’s look at the graph of y = 2x + 3.

The straight line y = 2x + 3 will pass through the points (- 2, – 1) and (2, 7). Here is how the graph looks like:

From the Fig.1 above, you can see that the graph of y = 2x + 3 intersects the x-axis at the point (- 3/2, 0). Now, the zero of (2x + 3) is (- 3/2). Therefore, the zero of the linear polynomial (2x + 3) is the x-coordinate of the point where the graph of y = 2x + 3 intersects the x-axis. Hence, we can say,

For a linear polynomial ax + b, a ≠ 0, the graph of y = ax + b is a straight line which intersects the x-axis at exactly one point, namely, (- b/a, 0). Also, this linear polynomial has only one zero which is the x-coordinate of the point where the graph of y = ax + b intersects the x-axis.

Browse more Topics under Polynomials

• Polynomial and its Types
• Value of Polynomial and Division Algorithm
• Degree of Polynomial
• Factorisation of Polynomials
• Remainder Theorem
• Factor Theorem
• Zeroes of Polynomial

Download NCERT Solutions for Class 10 Maths

Quadratic Polynomial

Let’s look at a quadratic polynomial, x 2 – 3x – 4. To look at the graph of y = x 2 – 3x – 4, let’s list some values:

The graph of y = x 2 – 3x – 4 will pass through (- 2, 6), (- 1, 0), (0, – 4), (1, – 6), (2, – 6), (3, – 4), (4, 0) and (5, 6). Here is how the graph looks:

For that matter, for any quadratic polynomial y = ax 2 + bx + c, a ≠ 0, the graph of y = ax 2 + bx + c has either one of these two shapes:

• If a > 0, then it is open upwards like the one shown in the graph above
• If a < 0, then it is open downwards.

These curves are parabolas . A quick look at the table above shows that (-1) and (4) are zeroes of the quadratic polynomial. From the Fig. 2 above, you can see that (-1) and (4) are the x-coordinates of the points where the graph of y = x 2 – 3x – 4 intersects the x-axis. Therefore, we can say,

The zeroes of a quadratic polynomial ax 2 + bx + c, a ≠ 0, are precisely the x-coordinates of the points where the parabola representing y = ax 2 + bx + c intersects the x-axis.

As far as the shape of the graph is concerned, the following three cases are possible:

The graph cuts x-axis at two distinct points A and A′, where the x-coordinates of A and A′ are the two zeroes of the quadratic polynomial ax 2 + bx + c, as shown below:

The graph intersects the x-axis at only one point, or at two coincident points. Also, the x-coordinate of A is the only zero for the quadratic polynomial ax2 + bx + c, as shown below:

The graph is either

• Completely above the x-axis or
• Completely below the x-axis.

So, it does not cut the x-axis at any point. Hence, the quadratic polynomial ax 2 + bx + c has no zero, as shown below:

To summarize, a quadratic polynomial can have either:

• Two distinct zeroes (as shown in Case i)
• Two equal zeroes (or one zero as shown in Case ii)
• No zero (as shown in Case iii)

It can also be summarized by saying that a polynomial of degree 2 has a maximum of 2 zeroes.

Cubic Polynomial

Let’s look at a cubic polynomial, x 3 – 4x. Next, let’s list a few values to plot the graph of y = x 3 – 4x.

The graph of y = x 3 – 4x will pass through (- 2, 0), (- 1, 3), (0, 0), (1, – 3), and (2, 0). Here is how the graph looks like:

From the table above, we can see that 2, 0 and – 2 are the zeroes of the cubic polynomial x 3 – 4x. You can also observe that the graph of y = x3 – 4x intersects the x-axis at 2, 0 and – 2. Let’s take a quick look at some examples:

Let’s plot the graph of the following two cubic polynomials:

The graphs of y = x 3 and y = x 3 – x 2 look as follows:

From the first graph, you can observe that 0 is the only zero of the polynomial x 3 , since the graph of y = x 3 intersects the x-axis only at 0. Similarly, the polynomial x 3 – x 2 = x 2 (x – 1) has two zeroes, 0 and 1. From the second diagram , you can see that the graph of y = x 3 – x 2 intersects the x-axis at 0 and 1.

Hence, we can conclude that there is a maximum of three zeroes for any cubic polynomial. Or, any polynomial with degree 3 can have maximum 3 zeroes. In general,

Given a polynomial p(x) of degree n, the graph of y = p(x) intersects the x-axis at a maximum of n points. Therefore, a polynomial p(x) of degree n has a maximum of n zeroes.

Solved Examples for You

Question 1: The graphs of y = p(x) are given in the figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Answer : The number of zeroes in each of the graphs above are:

• 0, since the line is not intersecting the x-axis.
• 1, since the line intersects the x-axis once.
• 2, since the line intersects the x-axis twice.
• 4, since the line intersects the x-axis four times.
• 3, since the line intersects the x-axis thrice.

Question 2:  What is meant by zeros of the function?

Answer: The zero of a function refers to any replacement for the variable that shall result in an answer of zero. Graphically, the real zero of a function is where the function’s graph crosses the x‐axis. So, the real zero of a function is the x‐intercept(s) of the function’s graph.

Question 3: How can one find zeroes in a function?

Answer: In order to find the zero of a function, one must find the point (a, 0) where the intersection of the function’s graph and the y-intercept takes place. In order to find the value of a from the point (a, 0), one must set the function equal to zero. Afterwards, one must try to solve for x.

Question 4: How many zeroes exist in a linear polynomial?

Answer: A linear polynomial consists of only 1 zero. In contrast, a quadratic polynomial consists of 2 zeroes while a cubic polynomial consists of 3 zeroes.

Question 5: Explain the zeroes in an equation?

Answer: The zeros of a quadratic equation refer to the points where the crossing of the graph of the quadratic equation takes place to the x-axis.

Customize your course in 30 seconds

Which class are you in.

Polynomials

• Polynomial and Its Types
• Factorization of Polynomials

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

Talk to our experts

1800-120-456-456

Graph of a Quadratic Polynomial for JEE

• Graph Of Quadratic Polynomial

What is a Quadratic Polynomial?

A polynomial is any expression in mathematics that has one or more algebraic terms along with numerical values. A polynomial function can comprise completely of variable terms as well. A few examples of polynomial functions will be the quadratic and cubic functions. Even a linear function in the form of y = mx+ x will be considered a linear polynomial whose graph is a straight line.

A quadratic polynomial is a mathematical expression where the highest power or degree of the variables is 2. Quadratic polynomials trace a different curve when plotted and graphed on the sheet. The graph of a quadratic polynomial is a parabola. Depending on the values of the coefficients in the expression and the discriminant, we get either a parabola opening upwards or downwards when x is the independent variable. Again, if the quadratic expression is in terms of y where the x is the dependable variable, the parabola will open either towards the right or towards the left. 

Graph of Quadratic Polynomial

As mentioned before, the quadratic polynomial graph is a parabola. If the polynomial function has x as the independent variable, then the roots of the quadratic expression give us the points where the graph cuts the x-axis. Similarly, if the quadratic function is in terms of y as the independent variable, then the roots of the function will give us the point of intersection of the y-axis and the parabolic curve.

To draw the graph of a quadratic polynomial we must follow the steps given below:

Let the given polynomial by $f(x)=a x^{2}+b x+c$. This is a quadratic function with x as the independent variable and a, b, and c are the arbitrary constants of the expression. 

Next, we write the given quadratic function as a y that is $y=f(x)=a x^{2}+b x+c$

The third step is to calculate the zeroes of the quadratic polynomial by equation y to 0. This goes as follows: $y=f(x)=a x^{2}+b x+c=0$

To get the points where the parabolic curve meets the y axis, we replace x with 0.

Lastly we calculate the value of the discriminant of the quadratic function that is given by $D=b^2-4ac$. 

When D > 0, the graph intersects the x-axis at two distinct points which are given by the roots of the functions

When D = 0, the parabolic graph touches the x-axis at one single point.

When D < 0, the graph does not touch the axis and lies far away. 

The last step is to find the turning point of the curve which has the coordinates    $\left(-\dfrac{b}{2a},~-\dfrac{D}{4a}\right)$. 

For drawing on the graph, we must plot the x values and their corresponding y values. By plotting these points on the graph we can easily draw the graph of a quadratic polynomial. If the value of the coefficient of the squared x term i.e. a > 0 then the parabola opens upwards. If a <0 the parabola will open downwards

To understand this further, we take the following quadratic polynomial example:

Example : Let the given quadratic polynomial function be $f(x)=x^{2}+2 x-3$. Draw the graph of the given quadratic function.

To solve this example we will follow the exact steps mentioned above. 

Let $f(x)=x^{2}+2 x-3$. Comparing the given polynomial with the standard form we get that, a = 1, b = 2 and  c= -3.

Since a > 0, the parabola will open upwards. 

Next, we calculate the discriminant, $D=b^2-4ac=2^2-4(1)(-3)=16$

As we can see D > 0. Therefore the parabola will intersect the x-axis at two distinct points which will give us the roots of the quadratic polynomial.

Equation y and 0, we get $x^{2}+2 x-3=0$.

Simplifying we get, $x^{2}+2 x-3=0 \Rightarrow x(x+3)-1(x+3)=0 \Rightarrow(x-1)(x+3)=0$

From the above expression we can find out the roots of the given quadratic function to be 1 and -3. i.e. either x = 1 or x = (-3)

Thus the graph intersects the x-axis at points ( 1 ,0 ) and ( -3,0 ). 

The vertex of the parabola is given by $\left(-\dfrac{b}{2 a},-\dfrac{D}{4 a}\right)=\left(-\dfrac{2}{2},-\dfrac{16}{4}\right)=(-1,-4)$

The required polynomial chart to draw the graph will be given as follows:

Required Table

Image 1: Table showing the x and y values for $y=x^{2}+2 x-3$

Therefore the required graph that we obtain from plotting all the points is as follows: 

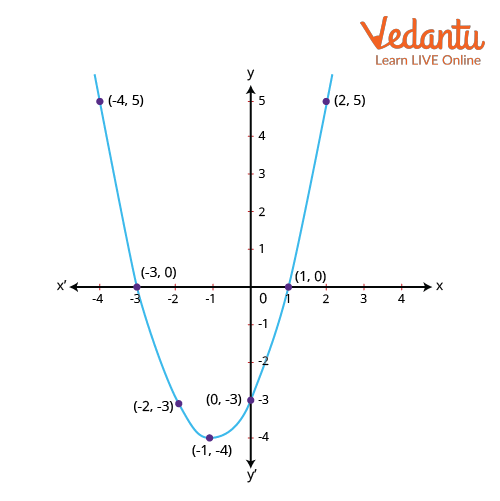
Parabolic Graph of $y=x^{2}+2 x-3$

Relationship Between Zeros of a Quadratic Polynomial and its Roots

Let us consider the quadratic polynomial, $y=f(x)=ax^2+bx+c$. Let α and β be the zeros of the polynomial. As per the factor theorem, we get $(x-\alpha)$ and $(x-\beta)$ are the factors of the given quadratic polynomial.

Therefore, $f ( x ) = k ( x – \alpha)  (x – \beta)$ 

$\Rightarrow a x^{2}+b x+c=k\left\{x^{2}-(\alpha+\beta) x+\alpha \beta\right\}=k x^{2}-(k \alpha+\beta) x+k \alpha \beta$

Thus comparing the coefficients  of the terms of the quadratic function we get, $\alpha + \beta = -\dfrac{b}{a}$ and $\alpha\beta = \dfrac{c}{a}$ 

Therefore the sum of the zeroes is given by $\left( -\dfrac{b}{a}\right)$ and the product of the zeroes is given by $\left(\dfrac{c}{a}\right)$. 

A quadratic polynomial is any mathematical expression constituting numerical coefficients and variables. The highest degree of power of the variable in this context is 2. The graph of a quadratic polynomial is a parabola. If the coefficient of the x 2 term is positive then the parabola will open upwards. If the coefficient of t he x 2 te rm is less than 0, then the parabola opens upwards. The value of the discriminant gives us the position of the curve on the graph. When D= 0 the graph intersects the x-axis and at D > 0 and D < 0, the curve touches the axis at a single point and lies above the axis, respectively. The relations between the roots of a quadratic polynomial and its roots are given as follows: $\alpha + \beta = -\dfrac{b}{a}$ and $\alpha\beta = \dfrac{c}{a}$ 

FAQs on Graph of a Quadratic Polynomial for JEE

1. What is the relationship between roots and zeros of a cubic function? What is the definition of a cubic polynomial's zeros?

Just as we see in the case of quadratic equation, the relationship between the roots and zeros is given as follows:

$\text{sum of the zeroes}=-\left(\dfrac{\text{coefficient of}~x^2}{\text{coefficient of}~x^3}\right)$

$\text{Product of the zeroes}=-\left(\dfrac{\text{the constant term}}{\text{coefficient of}~x^3}\right)$

The cubic polynomial has the form $a x^{3}+b x^{2}+c x+d$, with the zeros, and. We know the relationship between the polynomial's sum and the product of its zeroes and coefficients. The zeros of a polynomial are the points where the polynomial as a whole becomes zero. 

2. What is the meaning of the term "quadratic equation"? How can you decide whether a graph is quadratic or not?

In mathematics, a quadratic problem is one in which a variable is multiplied by itself, which is known as squares. The size of a square is equal to its side length multiplied by itself in this language. The word "quadratic" comes from the Latin word quadratum, which means "square."The easiest way to see whether the graph is that of a quadratic function or not, we simply need to check the curve. A quadratic function always exhibits a parabolic curve. 

Thus, we can simply check whether the shape traced is a parabola or not to check whether the function is quadratic in nature or not. 

• Math Article
• Polynomial For Class 10

Polynomial Class 10 Notes: Chapter 2

Cbse class 10 maths notes polynomial:- download pdf here, class 10 maths chapter 2 polynomial notes.

CBSE Class 10 Maths Chapter 2 Polynomial Notes are provided here in detail. Here, we are going to discuss the complete explanation of what is polynomial and its types, algebraic expressions, degree of a polynomial expression, graphical representation of the polynomial equations, factorization, relationship between zeroes and coefficient of a polynomial, and so on with many examples.

Students can refer to the short notes and MCQ questions along with separate solution pdf of this chapter for quick revision from the links below:

• Polynomials Short Notes
• Polynomials MCQ Practice Questions
• Polynomials MCQ Practice Solutions

Algebraic Expressions

An algebraic expression is an expression made up of variables and constants along with mathematical operators. An algebraic expression is a sum of terms, which are considered to be building blocks for expressions.

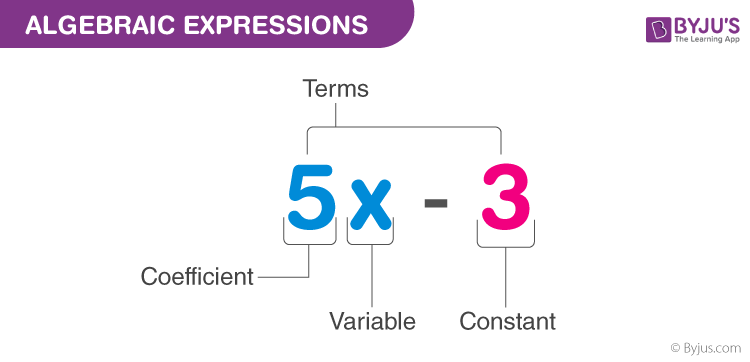
A term is a product of variables and constants. A term can be an algebraic expression in itself. Examples of a term – 3, which is just a constant. – 2x, which is the product of constant ‘2’ and the variable ‘x’ – 4xy, which is the product of the constant ‘4’ and the variables ‘x’ and ‘y’. – 5x 2 y, which is the product of 5, x, x and y.

The constant in each term is referred to as the coefficient.

Example of an algebraic expression: 3x 2 y+4xy+5x+6 which is the sum of four terms: 3x2y, 4xy, 5x and 6.

An algebraic expression can have any number of terms . The coefficient in each term can be any real number . There can be any number of variables in an algebraic expression. The exponent on the variables, however, must be rational numbers.

To know more about Algebraic Expressions, visit here .

An algebraic expression can have exponents that are rational numbers. However, a polynomial is an algebraic expression in which the exponent on any variable is a whole number.

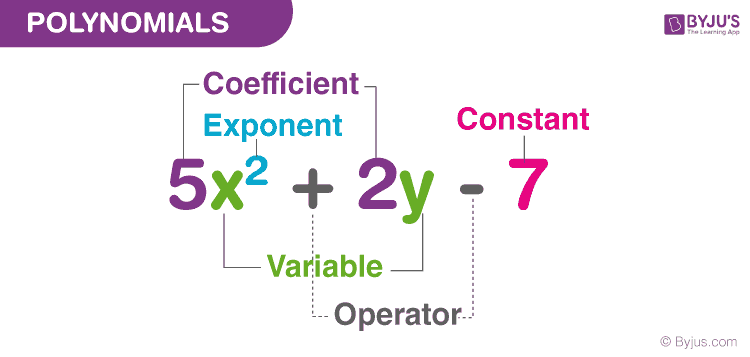
Let us consider a few more examples, 5x 3 +3x+1 is an example of a polynomial. It is an algebraic expression as well.

2x+3√x is an algebraic expression but not a polynomial. – since the exponent on x is 1/2, which is not a whole number.

To know more about polynomials, visit here .

Degree of a Polynomial

For a polynomial in one variable – the highest exponent on the variable in a polynomial is the degree of the polynomial.

Example: The degree of the polynomial x 2 +2x+3 is 2, as the highest power of x in the given expression is x 2 . Consider another example, the degree of the polynomial x 8 + 2x 6 – 3x + 9 is 8 since the greatest power in the given expression is 8.

Types Of Polynomials

Polynomials can be classified based on the following. a) Number of terms b) Degree of the polynomial.

Types of Polynomials Based on the Number of Terms

a) Monomial – A polynomial with just one term. Example: 2x, 6x 2 , 9xy

b) Binomial – A polynomial with two unlike terms. Example: 4x 2 +x, 5x+4

a) Trinomial – A polynomial with three unlike terms. Example: x 2 +3x+4

Types of Polynomials based on Degree

Linear Polynomial

A polynomial whose degree is one is called a linear polynomial. For example, 2x+1 is a linear polynomial.

Quadratic Polynomial

A polynomial of degree two is called a quadratic polynomial. For example, 3x 2 +8x+5 is a quadratic polynomial.

To know more about the types of polynomials, click here .

For more information on Quadratic Polynomials, watch the below video

Cubic Polynomial

A polynomial of degree three is called a cubic polynomial . For example, 2x 3 +5x 2 +9x+15 is a cubic polynomial.

Graphical Representations

Let us learn here how to represent polynomial equations on the graph.

Representing Equations on a Graph

Any equation can be represented as a graph on the Cartesian plane, where each point on the graph represents the x and y coordinates of the point that satisfies the equation. An equation can be seen as a constraint placed on the x and y coordinates of a point, and any point that satisfies that constraint will lie on the curve.

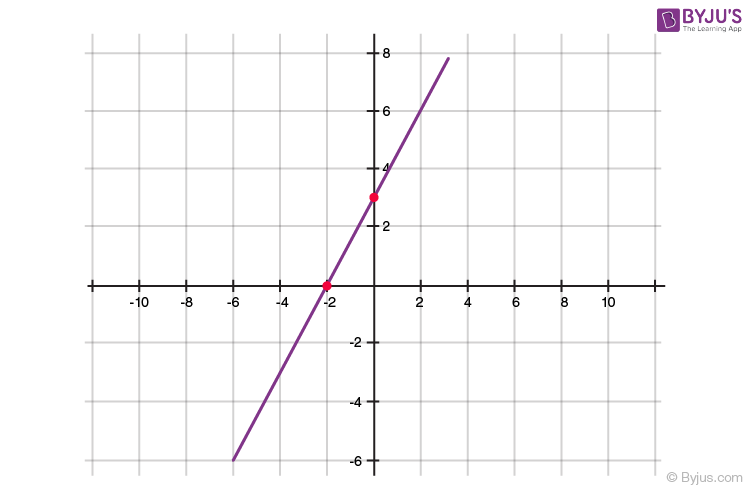
Geometrical Representation of a Linear Polynomial

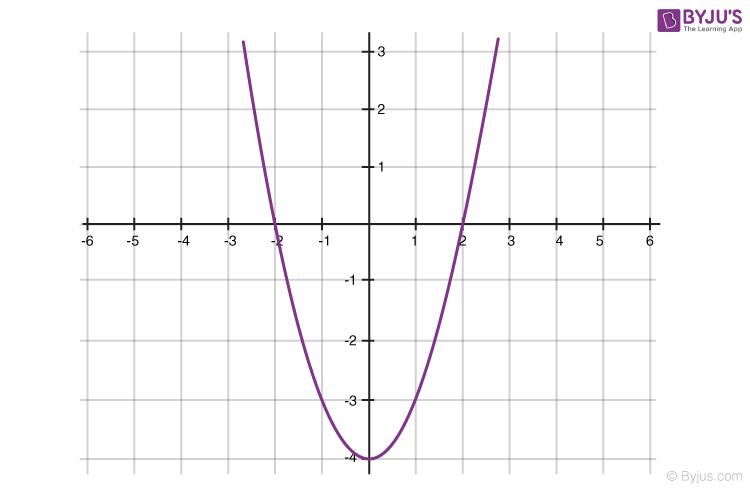
Geometrical Representation of a Quadratic Polynomial

• The graph of a quadratic polynomial is a parabola
• It looks like a U, which either opens upwards or opens downwards depending on the value of ‘a’ in ax 2 +bx+c
• If ‘a’ is positive, then parabola opens upwards and if ‘a’ is negative then it opens downwards
• It can cut the x-axis at 0, 1 or two points

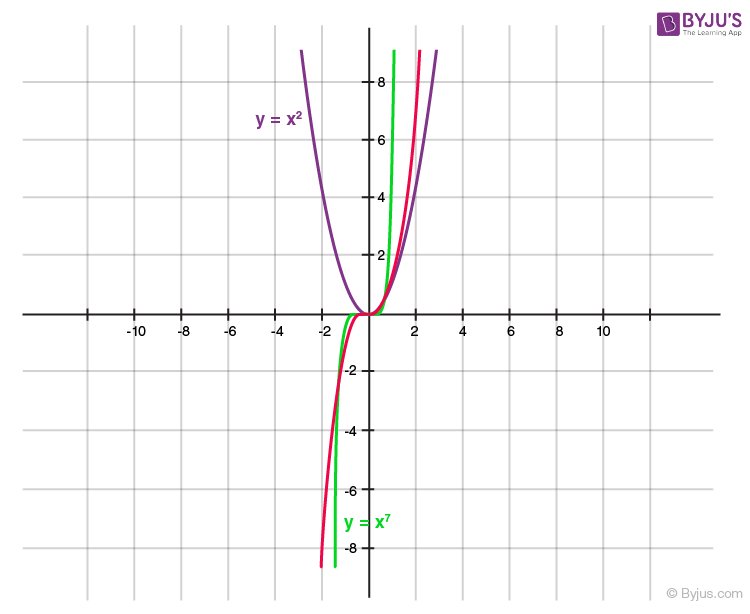
Graph of the Polynomial x^n

For a polynomial of the form y=x n where n is a whole number:

• as n increases, the graph becomes steeper or draws closer to the Y-axis
• If n is odd, the graph lies in the first and third quadrants
• If n is even, the graph lies in the first and second quadrants
• The graph of y=−x n is the reflection of the graph of y=x n on the x-axis

Zeroes of a Polynomial

A zero of a polynomial p(x) is the value of x for which the value of p(x) is 0. If k is a zero of p(x), then p(k)=0.

For example, consider a polynomial p(x)=x 2 −3x+2.

When x=1, the value of p(x) will be equal to

p(1)=12−3×1+2

Since p(x)=0 at x=1, we say that 1 is a zero of the polynomial x 2 −3x+2

Video Lesson on Zeroes of Polynomials

To know more about Zeroes of a Polynomial, visit here .

Geometrical Meaning of Zeros of a Polynomial

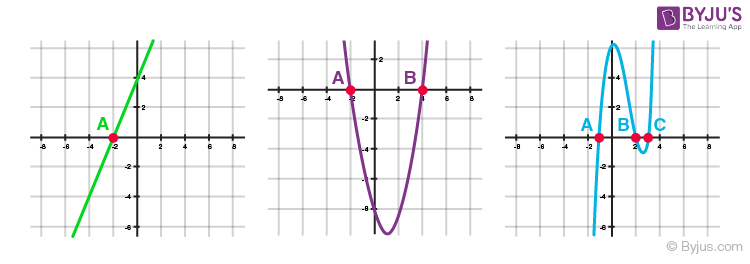
Here A, B and C correspond to the zeros of the polynomial represented by the graphs.

Number of Zeros

In general, a polynomial of degree n has at most n zeros.

• A linear polynomial has one zero,
• A quadratic polynomial has at most two zeros.
• A cubic polynomial has at most 3 zeros.

Factorisation of Polynomials

Quadratic polynomials can be factorized by splitting the middle term.

For example, consider the polynomial 2x 2 −5x+3

Splitting the middle term:

The middle term in the polynomial 2x 2 −5x+3 is -5x. This must be expressed as a sum of two terms such that the product of their coefficients is equal to the product of 2 and 3 (coefficient of x 2 and the constant term)

−5 can be expressed as (−2)+(−3), as −2×−3=6=2×3

Thus, 2x 2 −5x+3=2x 2 −2x−3x+3

Now, identify the common factors in individual groups

2x 2 −2x−3x+3=2x(x−1)−3(x−1)

Taking (x−1) as the common factor, this can be expressed as:

2x(x−1)−3(x−1)=(x−1)(2x−3)

For more information on Factorisation Of Quadratic Polynomials, watch the below video

To know more about Factorisation of Polynomials, visit here .

Relationship between Zeroes and Coefficients of a Polynomial

For Quadratic Polynomial: If α and β are the roots of a quadratic polynomial ax 2 +bx+c, then,

α +  β = -b/a

Sum of zeroes = -coefficient of x /coefficient of x 2

Product of zeroes = constant term / coefficient of x 2

For Cubic Polynomial

If α,β and γ are the roots of a cubic polynomial ax 3 +bx 2 +cx+d, then

α+β+γ = -b/a

αβ +βγ +γα = c/a

Calculate the sum of the zeroes and the product of the zeroes of the polynomial 9x 2 – 16x + 20.

Given polynomial: 9x 2 – 16x + 20

The given polynomial is a quadratic polynomial, as the degree of the polynomial is 2.

We know that the standard form of a quadratic polynomial is ax 2 + bx + c.

By comparing the given polynomial and the standard form, we can write.

By using the relationship between zeroes and the coefficients of the polynomial, we can get the following:

For a quadratic polynomial,

The sum of zeroes = -coefficient of x /coefficient of x 2

Now, substitute the values in the formula, we get

Sum of zeroes = -(-16)/9 = 16/9.

Similarly, Product of zeroes = constant term / coefficient of x 2

Plugging the values in the above formula, we get

Product of zeroes = 20/9

Hence, 16/9 and 20/9 are the sum and the product of the zeroes of the polynomial 9x 2 – 16x + 20.

To know more about Relationship between Zeroes and Coefficients of a Polynomial, visit here .

Division Algorithm

Let us assume that P(x) and G(x) are the two polynomials, such that G(x)≠ 0, then the division algorithm states the formula to find Q(x) and R(x) of the polynomial.

Here, P(x) denotes dividend polynomial

G(x) denotes divisor polynomial

Q(x) denotes quotient polynomial

R(x) denotes the remainder polynomial.

Thus, the formula stated by division algorithm is:

P(x) = G(x) × Q(x) + R(x)

To divide one polynomial by another, follow the steps given below.

Step 1: Arrange the terms of the dividend and the divisor in the decreasing order of their degrees.

Step 2: To obtain the first term of the quotient, divide the highest degree term of the dividend by the highest degree term of the divisor  Then carry out the division process.

Step 3: The remainder from the previous division becomes the dividend for the next step. Repeat this process until the degree of the remainder is less than the degree of the divisor.

Algebraic Identities

1. (a+b) 2 =a 2 +2ab+b 2

2. (a−b) 2 =a 2 −2ab+b 2

3. (x+a)(x+b)=x 2 +(a+b)x+ab

4. a 2 −b 2 =(a+b)(a−b)

5. a 3 −b 3 =(a−b)(a 2 +ab+b 2 )

6. a 3 +b 3 =(a+b)(a 2 −ab+b 2 )

7. (a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

8. (a−b) 3 =a 3 −3a 2 b+3ab 2 −b 3

For more information on Algebraic Identities, watch the below videos

To know more about Algebraic Identities, visit here .

Polynomials for Class 10 Examples

Determine the quadratic polynomial, whose zeroes are 5-3√2 and 5+3√2.

Given zeroes: 5-3√2 and 5+3√2.

Finding sum of zeroes:

Sum of zeroes = (5-3√2)+(5+3√2)

Sum of zeroes = 5+5 = 10.

Finding product of zeroes:

Product of zeroes = (5-3√2)(5+3√2)

We know that a 2 -b 2 = (a+b)(a-b).

Hence, (5) 2 – (3√2) 2 = (5-3√2)(5+3√2).

Therefore, product of zeroes = 25 – [9(2)]= 25 – 18 = 7

Thus, the required quadratic polynomial is:

P(x)= x 2 -(sum of zeroes)x + product of zeroes

P(x) = x 2 -10x+7.

Hence, the required quadratic polynomial is x 2 -10x+7.

Find the zeroes of the quadratic polynomial 6x 2 -3-7x. Also, verify the relationship between the zeroes and the coefficient of a polynomial.

Given quadratic polynomial: 6x 2 -3-7x.

Let P(x) = 6x 2 -3-7x.

We know that zero of a polynomial is a value of x, when P(x) = 0.

Hence, 6x 2 -7x-3 = 0

Now, factorize the above polynomial equation to find the value of x.

Thus, 6x 2 -7x – 3 = 0 is also written as:

6x 2 -9x+2x-3 = 0

3x(2x-3)+1(2x-3) = 0

(3x+1) (2x-3) =0

Thus, 3x+1 = 0 and 2x-3 =0

⇒3x+1 = 0

⇒2x-3 = 0

⇒x = 3/2.

Hence, the zeroes of the quadratic polynomial 6x 2 – 7x-3 are -1/3 and 3/2.

Thus, α = -1/3 and β = 3/2 are the zeroes of the polynomial.

Now, comparing P(x) = 6x 2 -7x-3 with ax 2 +bx+c.

Hence, a = 6, b=-7 and c = -3.

Verifying the Relationship Between Zeroes and Coefficient of Polynomial:

Sum of zeroes:

We know that the sum of zeroes = – coefficient of x/Coefficient of x 2 .

Thus, α+β = -b/a

Now, substitute the values, we get

(-1/3)+(3/2) = -(-7)/6

(-2+9)/6 = 7/6

Hence, LHS = RHS.

Product of Zeroes:

We know that the product of zeroes = Constant term/Coefficient of x 2 .

Therefore, αβ = c/a

On substituting the values, we get

(-1/3)(3/2) = (-3/6)

-1/2 = -1/2

Therefore, the relationship between the zeroes and coefficients of the polynomial 6x 2 -7x-3 is verified.

Stay tuned with BYJU’S – The Learning App and download the app to learn all class-wise concepts easily by exploring more videos.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

it was very useful

This notes helped me a lot.

Very helpful and best material ever!!!!!!!!!!!1111

nice its helpful

really it will help me in board exams

I learnt a lot of formulas through these notes

it is very useful for me

it has many useful questions related to class 10 exams .

I test myself in quiz thanks a lot

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Raspberry Pi

Introduction to quadratic equations with it's graphical representation.

• Introduction to Quadratic Equations.
• Solutions of a Quadratic Equation.
• Graphical Representation of Quadratic Equations.
• Methods to solve Quadratic Equation.
• Multiple Graphical Solutions of Quadratic Equations.
• Forms of  Quadratic Equations.
• Comparison between quadratic equations.

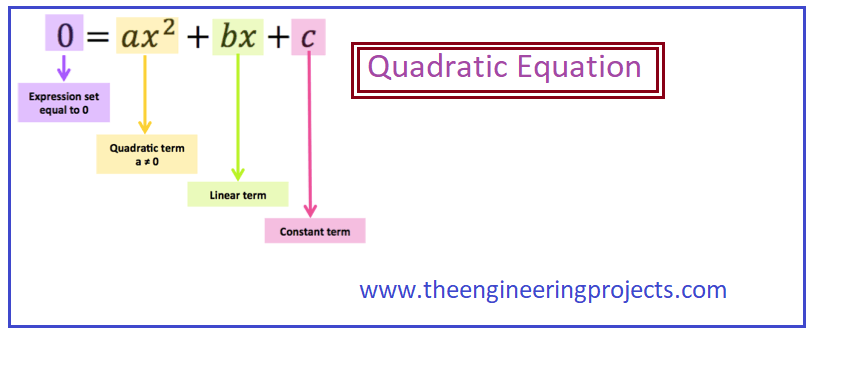
Introduction to Quadratic Equations

a0+a1x+a2x2+ . . . +anxn

where all a0, a1, a2, . . . ,an are constants which belong to the set of real numbers. Here we will just talk about 2nd degree polynomial. A 2nd degree polynomial of the form      ‘ax2+bx+c’  is called a quadratic polynomial and by equating equal to 0 we get a quadratic equation, which is:

ax2+bx+c=0 where a,b & c are constants and real numbers.

Hitory of Quadratic Equations

Possible solutions of a quadratic equation, solutions of a quadratic equation, graphical representation of quadratic equation.

How to Solve Quadratic Equations ?

1. quadratic formula.

• We can find solutions/roots of a quadratic equation by using simple a well known formula which is known as quadratic formula and is given below:

2. Method of Factorization

• Secondly, we can solve quadratic equation by another method which is known as method of Factorization.  This method is more clear from the following figure which shows step by step procedure to apply on some quadratic equation.

3. Method of Completing Square

• We can find roots of a quadratic equation by using method of Completing Suqare.

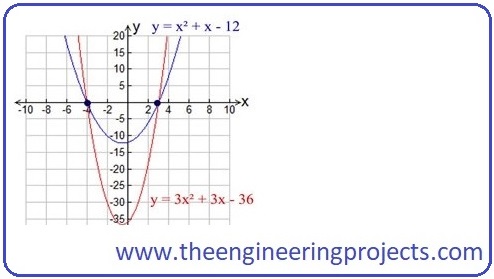
Comparison between Quadratic Equations

3x 2 +3x+-36=0              ,              x 2 +x+-12=0           

3(x 2 +x+-12)=0               ,             x 2 +4x-3x+-12=0      

 x 2 +x+-12=0                  ,              x (x+4) – 3 (x+4) =0

                                                      (x-3) (x+4)=0   and this shows x=3 and x=-4.

Syed Zain Nasir

IB Maths Resources from Intermathematics

IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides

Graphically Understanding Complex Roots

If you have studied complex numbers then you’ll be familiar with the idea that many polynomials have complex roots. For example x 2 + 1 = 0 has the solution x = i and -i.  We know that the solution to x 2 – 1 = 0 ( x = 1 and -1) gives the two x values at which the graph crosses the x axis, but what does a solution of x = i or -i represent graphically?

There’s a great post on Maths Fun Facts which looks at basic idea behind this and I’ll expand on this in a little more detail.  This particular graphical method only works with quadratics:

You have a quadratic graph with complex roots, say y = (x – 1) 2 + 4. Written in this form we can see the minimum point of the graph is at (1,4) so it doesn’t cross the x axis. Step 2

Reflect this graph downwards at the point of its vertex. We do this by transforming y = (x – 1) 2 + 4 into y =  -(x – 1) 2 + 4

We find the roots of this new equation using the quadratic formula or by rearranging – leaving the plus or minus sign in. -(x – 1) 2 + 4 = 0 (x-1) = ± 2 x = 1 ± 2

Plot a circle with centre (1,0) and radius of 2.  This will touch both roots.

We can now represent the complex roots of the initial equation by rotating the 2 real roots we’ve just found 90 degrees anti-clockwise, with the centre of rotation the centre of the circle.

The points B and C on the diagram are a representation of the complex roots (if we view the graph as representing the complex plane).  The complex roots of the initial equation are therefore given by x = 1 ± 2i.

General case

It’s relatively straightforward to show algebraically what is happening:

If we take the 2 general equations:

1) y = (x-a) 2 + b 2) y = -(x-a) 2 + b  (this is the reflection at the vertex of equation 1 )

(b > 0 ).  Then the first equation will always have complex roots.  The roots of both equations will be given by:

So we can think of (2) as representing a circle of radius √b, centred at (a,0).  Therefore multiplying √b by i has the effect of rotating the point (√b, 0 ) 90 degrees anti-clockwise around the point (a,0).  Therefore the complex roots will be graphically represented by those points at the top and bottom of this circle.  (a, √b) and (a, -√b)

Graphically finding complex roots of a cubic

There is also a way of graphically calculating the complex roots of a cubic with 1 real and 2 complex roots.  This method is outlined with an algebraic explanation here

We plot a cubic with 1 real and 2 complex roots, in this case y = x 3 – 9x 2 + 25x – 17.

We find the line which goes through the real root (1,0) and which is also a tangent to the function.

If the x co-ordinate of the tangent intersection with the cubic is a and the gradient of the tangent is m, then the complex roots are a ± (√m)i.  In this case the tangent x intersection is at 4 and the gradient of the tangent is 1, therefore the complex roots are 4 ± 1i.

[2nd last sentence edited – thanks for the comments below!]

Essential resources for IB students:

1) Exploration Guides  and Paper 3 Resources

I’ve put together four comprehensive pdf guides to help students prepare for their exploration coursework and Paper 3 investigations. The exploration guides talk through the marking criteria, common student mistakes, excellent ideas for explorations, technology advice, modeling methods and a variety of statistical techniques with detailed explanations. I’ve also made 17 full investigation questions which are also excellent starting points for explorations.  The Exploration Guides can be downloaded here  and the Paper 3 Questions can be downloaded here .

Share this:

6 thoughts on “ graphically understanding complex roots ”.

Thanks for simple explanation!

I believe that for the complex roots of a cubic the slope of the tangent line is the square of of the imaginary part. So if the line were 3x+4, the complex roots would be 3+2i and 3-2i.

If p is the real root and the complex roots are a + bi and a – bi, the equation of the tangent line is y = b^2 (x – p). The tangent line intersects the graph of the function at x = a.

The the tangent intercept is represented by (h,k) and the Tangent line is represented by Slope Intercept form (y=mX+b) than the actual zero is ; h±(the square root of m)

A more complete answer: All of the discussion so far (including my response of almost two years ago) assumes the leading coefficient is 1 which will guarantee the slope of the tangent line in question is positive. However if the cubic has leading coefficient of A (not equal to zero) the real part of the complex solutions remains the first coordinate of the intersection point but the imaginary parts are +/- the square root of m/A where m is the slope of the tangent line.

thanks for the replies – I have (belatedly!) updated.

Leave a Reply Cancel reply

Powered by WordPress.com .

Discover more from IB Maths Resources from Intermathematics

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading