
TRANSFORMATIONS & FUNCTIONS
Chapter 1 - Function Transformations
Chapter 2 - Radical Functions
Chapter 3 - Polynomial Functions
• UNIT 1 NOTES PACKAGE •
1.1 - HORIZONTAL & VERTICAL TRANSLATIONS
PG 12 #1-12
1.2 - REFLECTIONS & STRETCHES
PG 28 #1-4, 6, 7, 9, 14
1.3 - COMBINING TRANSFORMATIONS
TRANSFORMATIONS (handout)
PG 38 #1-11, 15
TRANSFORMATIONS CONT...
ANSWER KEY
1.4 - INVERSE OF A RELATION
PG 51 #1-10, 12, 15, 20
2.1 - RADICAL FUNCTIONS & TRANSFORMATIONS
PG 72 #1-7, 10, 11
2.2 - SQUARE ROOT OF A FUNCTION
PG 86 #3-11
2.3 - SOLVING RADICAL EQUATIONS GRAPHICALLY
PG 96 #3-9, 14, 16
3.1 - CHARACTERISTICS OF POLYNOMIAL FUNCTIONS
PG 114 #1-4, 6, 9, 11
3.2 (1) - THE REMAINDER THEOREM
PG 124 #1-5
3.2 (2) - THE REMAINDER THEOREM
PG 124 #6-10, 14, 15
3.3 - THE FACTOR THEOREM
PG 133 #3-7
3.3 - CONT...
3.4 (1) - solving polynomial equations, 3.4 ( 2 ) - zero of multiplicity.
PG 147 #1-7, 9, 10
unit 1 test cycle
REVIEW PAGES:
CH 1 - PG 56
CH 2 - PG 99
CH 3 - PG 153
UNIT 1 - PG 158
PRE-TEST - Wednesday, Oct 2nd
CORRECTIONS - Thursday, Oct 3rd
UNIT TEST - Friday, Oct 4th
CORRECTIONS - Monday, Oct 7th
RE-TEST - Tuesday, Oct 8th

Review of Transformations
Related Topics: More Lessons for High School Regents Exam Math Worksheets
High School Math based on the topics required for the Regents Exam conducted by NYSED.
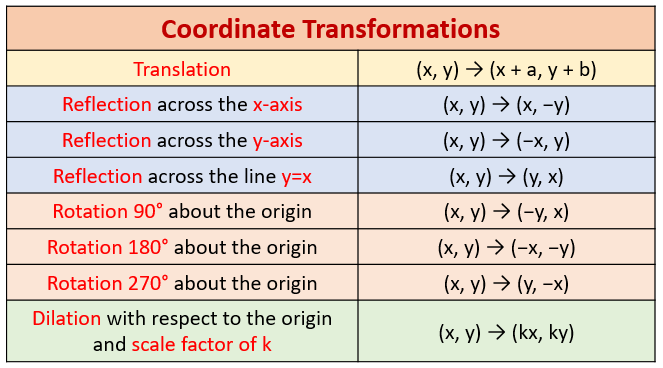
Translations Reflections Rotations Dilations
A reflection is a flip. It is an opposite isometry. This means that the image does not change size but the lettering is reversed. Reflection in the x-axis: R x-axis (x, y) = (x, -y) Reflection in the y-axis: R y-axis( x, y) = (-x, y) Reflection in the line y = x: R y = x( x, y) = (y, x) Reflection in the line y = -x, R y = -x (x, y) = (-y, -x)
A rotation turns a figure through an angle about a fixed point called the center. A positive angle of rotation turns the figure counterclockwise, and a negative angle of rotation turns the figure in a clockwise direction. It is a direct isometry - the order of the lettering in the figure and the image are the same. Rotation of 90° about the origin: R 90° (x, y) = (-y, x) Rotation of 180° (or point rotation about the origin) : R 180° (x, y) = (-x, -y) Rotation of 270° about the origin : R 270° (x, y) = (y, -x)
A translation “slides” an object a fixed distance in a given direction. The original object and its translation have the same shape and size, and they face in the same direction. It is a direct isometry - the order of the lettering in the figure and the image are the same. Translation of h, k : T h,k (x, y) = (x+h, y+k)
A dilation is a transformation that produces an image that is the same shape as the original, but is a different size. It is not an isometry and it forms similar figures.
Dilation of scale factor k with the center at the origin: D k (x, y) = (kx, ky)
Transformations - Reflection Review the rules for performing a reflection across the x-axis. When reflecting an object over the x-axis, keep all x-values and change the y-value. This tutorial reviews how to perform a reflection over the x-axis on the coordinate plane.
Transformations - Rotate 90 degrees This video reviews how to perform 90 degree rotations (clockwise and counterclockwise) around the origin.
Rotate 180 Degrees Around The Origin This tutorial shows why all signs of an ordered pair of an object become opposite when rotating that object 180 degrees around the origin.
Transformations - Translating a Polygon On The Coordinate Plane This tutorial reviews how to translate a given polygon on the coordinate plane.
Dilation Of Objects On The Coordinate Plane This tutorial reviews how to dilate an object on the coordinate plane when the center of dilation is the origin and also when the center of dilation is not the origin.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- Inspiration
Join the Mailing List
Search the blog.
Input your search keywords and press Enter.

Alyssa Teaches
an Upper Elementary Blog
6 Engaging Activities to Teach Geometric Transformations

I am all about making math lessons as hands-on as possible – especially during a geometry unit! I love using engaging activities to teach geometric transformations so that elementary students can practice manipulating objects in different ways.
Here are some of my favorite low-prep activities for teaching reflections, rotations, and translations (aka flips, slides, and turns).
Transformations Art Activities
If you’ve been looking for a way to incorporate art into your math lessons, a geometry unit is a great opportunity!
One of my favorite activities is to have students create art with the different types of transformations. In the past, my students have done this with polygons, letters and numbers, and even our names.
Students just design whatever template they want to use and trace it to create copies (this is a good review of congruency). Then, they can create a tri-fold with the original image and a reflection, rotation, and translation.

Do you collaborate with specialists to team-teach? This is definitely a standard that art teachers can support!
Use Math Manipulatives
Another low-prep, high-engagement way to teach geometric transformations is to break out the pattern blocks, tangram shapes, and geoboards . Students can create an original design and then pass their work to a partner to create a reflection, rotation, or translation with it. There are tons of free virtual pattern blocks that students can use, too.
If you have a set of small hand mirrors, those are also fun to use to teach reflections. Tip: Raid your science materials!
Digital Transformations Activities
I also recommend having students practice making geometric transformations on the screen. Knowing how to flip, slide, and rotate objects with a mouse or keypad helps improve their computer skills!
These digital activities make it fun for students to practice geometry standards on the computer. And they’re super easy to assign right in Google Classroom™.
Geometric Transformations Boom Cards
Boom cards are another great way to review reflections, rotations, and translations.
If you’re new to Boom, it’s a digital platform where students can complete task cards digitally – which is great TEI practice! These engaging Boom cards are great to use for a review activity, especially during spring test prep.

Bust Out the Dance Moves
Remember the Electric Slide and the Cha Cha Slide? Variations on these dances are a really fun way for students to practice geometric transformations with their own bodies! You can just call out different moves (“slide to the left”) and have them play. They’ll go nuts!
Transformations Cut and Paste
These free printable worksheets also provide good practice with the 3 transformations. I’d use this as a classwork or homework assignment, a review, or even an assessment!
As you can see, there are plenty of hands-on, high-engagement activities to teach 3rd, 4th, and 5th graders about geometric transformations. What other strategies do you use to teach translations, rotations, and reflections? Let me know in the comments!
Related posts

Daily 4th Grade Math SOL Word Problems

Teaching Factors and Multiples

5th Grade Math SOL Review Activities You’ll Want for Your Students
No comments, leave a reply cancel reply, join the mailing list for tips, ideas, and freebies.
- Mentor Teacher
- Organization
- Social Studies
- Teacher Tips
- Virginia Studies

- $ 0.00 0 items
Unit 2 – Transformations, Rigid Motions, and Congruence
Transformations
LESSON/HOMEWORK
LESSON VIDEO
EDITABLE LESSON
EDITABLE KEY
Reflections
Isosceles Triangles
Translations
Congruence and Rigid Motions
Basic Rigid Motion Proofs
Congruence Reasoning with Triangles
Symmetries of a Figure
Unit Review
Unit 2 Review – Transformations, Rigid Motions, and Congruence
UNIT REVIEW
EDITABLE REVIEW
Unit 2 Assessment Form A
EDITABLE ASSESSMENT
Unit 2 Assessment Form B
Unit 2 Assessment Form C
Unit 2 Assessment Form D
Unit 2 Exit Tickets
Unit 2 Mid-Unit Quiz (After Lesson #5) – Form A
Unit 2 Mid-Unit Quiz (After Lesson #5) – Form B
Unit 2 Mid-Unit Quiz (After Lesson #5) – Form C
Unit 2 Mid-Unit Quiz (After Lesson #5) – Form D
U02.AO.01 – 2 Kites (Enrichment)
EDITABLE RESOURCE
U02.AO.02 – Congruence and Rigid Motion Practice
U02.AO.03 – Isosceles Triangles – Extra Practice
U02.AO.04 – Polygon Symmetry and Mapping – Extra Practice
Thank you for using eMATHinstruction materials. In order to continue to provide high quality mathematics resources to you and your students we respectfully request that you do not post this or any of our files on any website. Doing so is a violation of copyright. Using these materials implies you agree to our terms and conditions and single user license agreement .
The content you are trying to access requires a membership . If you already have a plan, please login. If you need to purchase a membership we offer yearly memberships for tutors and teachers and special bulk discounts for schools.
Sorry, the content you are trying to access requires verification that you are a mathematics teacher. Please click the link below to submit your verification request.

IMAGES
VIDEO
COMMENTS
Unit One Notes and Assignments. Transformation Vocabulary NOTES and ASSIGNMENT and KEY. Translation NOTES and ASSIGNMENT and KEY. Reflection NOTES and ASSIGNMENT and KEY. . Rotation NOTES and ASSIGNMENT and KEY. Transformation Review worksheets. All . Transformations and KEY.
Compositions of Transformations A _____, also known as composition of transformations is a series of multiple transformations performed one after the other. Directions: • Graph the original coordinates. • Then, apply the listed transformations. • Graph the new images. • Be sure to draw each new image in a new color.
Study with Quizlet and memorize flashcards containing terms like Determine the parent function., Identify the equation of the function., How do you translate the graph of f(x) = x3 left 4 units and down 2 units? Identify the equation of the graph. y = (x - 4)³ - 2y = (x + 4)³ - 2y = (x + 2)³ - 4y = (x - 2)³ - 4 and more.
1 Copy each diagram onto squared paper and enlarge or reduce with centre C and the scale factor k given: 8 Find the image of: a (2, 3) under a clockwise 900 rotation about 0(0, O) followed by a reflection in the x-axis —x followed by a trailslation of ( 1 b (—2, 5) under a reflection in y c (4, —1) under a reflection in y = x followed by ...
1. First draw lines from the corners of the shape through (0,0) and extending them beyond. Since the scale factor is -2, we know the shape will be on the opposite side of the centre of enlargement. 2. Multiply the distance between the corner of the shape and the centre of enlargement by 2 (since the scale factor is -2) and measure this distance ...
G-CO.2: Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch)
Free lessons, worksheets, and video tutorials for students and teachers. Topics in this unit include: translations, stretches, compressions, and reflections of parent functions, and inverse functions. This follows chapter 2 of the grade 11 Functions McGraw Hill textbook and chapter 1 of the grade 11 Functions Nelson textbook.
TRANSFORMATIONS & FUNCTIONS. Chapter 1 - Function Transformations. Chapter 2 - Radical Functions. Chapter 3 - Polynomial Functions ... REVIEW PAGES: CH 1 - PG 56. CH 2 - PG 99. CH 3 - PG 153. UNIT 1 - PG 158. SCHEDULE: PRE-TEST - Wednesday, Oct 2nd. CORRECTIONS - Thursday, Oct 3rd.
Transformations - Reflection. Review the rules for performing a reflection across the x-axis. When reflecting an object over the x-axis, keep all x-values and change the y-value. This tutorial reviews how to perform a reflection over the x-axis on the coordinate plane. Show Step-by-step Solutions. Transformations - Rotate 90 degrees.
In this activity, students apply translations, reflections, and dilations to various functions and observe the graphical effects. The first set of challenges involves function notation. Later challenges invoke "y equals" form for four parent functions: absolute value, quadratic, cubic, and square root. Each challenge comes with a "check your ...
Unit 7 Review - Transformations of Functions UNIT REVIEW. ANSWER KEY. EDITABLE REVIEW. EDITABLE KEY. ... Transformation Graphing Activity - Teacher Directions RESOURCE. EDITABLE RESOURCE. ... If you create a modified assignment using a purchased editable file, please credit us as follows on all assignment and answer key pages: ...
tion using a compass and straightedge. CA'. ideo: Constructing Transformations Chapter 2 Wksht #8Placing the compass pointer at point A make a circl. of any radius as long as it intersects. ne m twice. In this case, name them points C and D.Leaving the compass radius the same - place the compass p.
all side lengths of JKL equal 2 units. a transformation maps JKL to J'K'L. the length of side J'K' is 5 units. is this a rigid transformaiton? B. A rigid transformation can also be referred to as an isometric transformation. The prefix "iso-" means "of the same" and "-metric" means "measure."
A quick review of transformations in the coordinate plane. ("Isometry" is another term for "rigid transformation".) Remember that a reflection is simply a flip. Under a reflection, the figure does not change size (it is a rigid transformation or isometry). It is simply flipped over the line of reflection.
Which describes the transformations of y = f (x) that would result in the graph of y = f (-x) - 7. Study with Quizlet and memorize flashcards containing terms like Which is the graph of y=2/x+2 ?, Consider a rectangle with width of x units and an area of 10 square units. The length l of the rectangle can be modeled by the function l (x)=10/x.
A transformation changes the position of a figure. Learn all about 4 common types of transformations in this free geometry lesson. Start learning now!
Transformations Cut and Paste. These free printable worksheets also provide good practice with the 3 transformations. I'd use this as a classwork or homework assignment, a review, or even an assessment! As you can see, there are plenty of hands-on, high-engagement activities to teach 3rd, 4th, and 5th graders about geometric transformations.
Feedback-Review Assignment - Transformations; Pc12 04 review; Related documents. Module 1 lesson 5; Lab 10 - Lab assignment for composite functions. Lab 8 - Lab assignment for trig functions. Graded at 100% (not shown) Lab 6 - Lab assignment for rational functions. 0a - dont read this its nithing;
Unit 2 Review - Transformations, Rigid Motions, and Congruence UNIT REVIEW. ANSWER KEY. EDITABLE REVIEW. EDITABLE KEY. Assessment Unit 2 Assessment Form A ASSESSMENT. ANSWER KEY ... If you create a modified assignment using a purchased editable file, please credit us as follows on all assignment and answer key pages:
WORK SAMPLE ASSIGNMENT CHAPTER 7Section 7.1: Scale Diagrams and EnlargementsSection 7.2: Scale Diagrams and ReductionsSection 7.3: Similar PolygonsSection 7.4: Similar TrianglesSection 7.5: Reflections and Line SymmetrySection 7.6: Rotations and Rotational SymmetrySection 7.7: Identifying Types of Symmetry on the Cartesian PlaneUnit 7 Outcomes.