statements about hypothesis testing is true

• Comprehensive Learning Paths
• 150+ Hours of Videos
• Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

8.1 The Elements of Hypothesis Testing

Learning objectives.

• To understand the logical framework of tests of hypotheses.
• To learn basic terminology connected with hypothesis testing.
• To learn fundamental facts about hypothesis testing.

Types of Hypotheses

A hypothesis about the value of a population parameter is an assertion about its value. As in the introductory example we will be concerned with testing the truth of two competing hypotheses, only one of which can be true.

The null hypothesis The statement that is assumed to be true unless there is convincing evidence to the contrary. , denoted H 0 , is the statement about the population parameter that is assumed to be true unless there is convincing evidence to the contrary .

The alternative hypothesis A statement that is accepted as true only if there is convincing evidence in favor of it. , denoted H a , is a statement about the population parameter that is contradictory to the null hypothesis, and is accepted as true only if there is convincing evidence in favor of it.

Hypothesis testing A statistical procedure in which a choice is made between a null hypothesis and a specific alternative hypothesis based on information in a sample. is a statistical procedure in which a choice is made between a null hypothesis and an alternative hypothesis based on information in a sample.

The end result of a hypotheses testing procedure is a choice of one of the following two possible conclusions:

• Reject H 0 (and therefore accept H a ), or
• Fail to reject H 0 (and therefore fail to accept H a ).

The null hypothesis typically represents the status quo, or what has historically been true. In the example of the respirators, we would believe the claim of the manufacturer unless there is reason not to do so, so the null hypotheses is H 0 : μ = 75 . The alternative hypothesis in the example is the contradictory statement H a : μ < 75 . The null hypothesis will always be an assertion containing an equals sign, but depending on the situation the alternative hypothesis can have any one of three forms: with the symbol “<,” as in the example just discussed, with the symbol “>,” or with the symbol “≠” The following two examples illustrate the latter two cases.

A publisher of college textbooks claims that the average price of all hardbound college textbooks is $127.50. A student group believes that the actual mean is higher and wishes to test their belief. State the relevant null and alternative hypotheses.

The default option is to accept the publisher’s claim unless there is compelling evidence to the contrary. Thus the null hypothesis is H 0 : μ = 127.50 . Since the student group thinks that the average textbook price is greater than the publisher’s figure, the alternative hypothesis in this situation is H a : μ > 127.50 .

The recipe for a bakery item is designed to result in a product that contains 8 grams of fat per serving. The quality control department samples the product periodically to insure that the production process is working as designed. State the relevant null and alternative hypotheses.

The default option is to assume that the product contains the amount of fat it was formulated to contain unless there is compelling evidence to the contrary. Thus the null hypothesis is H 0 : μ = 8.0 . Since to contain either more fat than desired or to contain less fat than desired are both an indication of a faulty production process, the alternative hypothesis in this situation is that the mean is different from 8.0, so H a : μ ≠ 8.0 .

In Note 8.8 "Example 1" , the textbook example, it might seem more natural that the publisher’s claim be that the average price is at most $127.50, not exactly $127.50. If the claim were made this way, then the null hypothesis would be H 0 : μ ≤ 127.50 , and the value $127.50 given in the example would be the one that is least favorable to the publisher’s claim, the null hypothesis. It is always true that if the null hypothesis is retained for its least favorable value, then it is retained for every other value.

Thus in order to make the null and alternative hypotheses easy for the student to distinguish, in every example and problem in this text we will always present one of the two competing claims about the value of a parameter with an equality. The claim expressed with an equality is the null hypothesis. This is the same as always stating the null hypothesis in the least favorable light. So in the introductory example about the respirators, we stated the manufacturer’s claim as “the average is 75 minutes” instead of the perhaps more natural “the average is at least 75 minutes,” essentially reducing the presentation of the null hypothesis to its worst case.

The first step in hypothesis testing is to identify the null and alternative hypotheses.

The Logic of Hypothesis Testing

Although we will study hypothesis testing in situations other than for a single population mean (for example, for a population proportion instead of a mean or in comparing the means of two different populations), in this section the discussion will always be given in terms of a single population mean μ .

The null hypothesis always has the form H 0 : μ = μ 0 for a specific number μ 0 (in the respirator example μ 0 = 75 , in the textbook example μ 0 = 127.50 , and in the baked goods example μ 0 = 8.0 ). Since the null hypothesis is accepted unless there is strong evidence to the contrary, the test procedure is based on the initial assumption that H 0 is true. This point is so important that we will repeat it in a display:

The test procedure is based on the initial assumption that H 0 is true.

The criterion for judging between H 0 and H a based on the sample data is: if the value of X - would be highly unlikely to occur if H 0 were true, but favors the truth of H a , then we reject H 0 in favor of H a . Otherwise we do not reject H 0 .

Supposing for now that X - follows a normal distribution, when the null hypothesis is true the density function for the sample mean X - must be as in Figure 8.1 "The Density Curve for " : a bell curve centered at μ 0 . Thus if H 0 is true then X - is likely to take a value near μ 0 and is unlikely to take values far away. Our decision procedure therefore reduces simply to:

• if H a has the form H a : μ < μ 0 then reject H 0 if x - is far to the left of μ 0 ;
• if H a has the form H a : μ > μ 0 then reject H 0 if x - is far to the right of μ 0 ;
• if H a has the form H a : μ ≠ μ 0 then reject H 0 if x - is far away from μ 0 in either direction.

Figure 8.1 The Density Curve for X - if H 0 Is True

Think of the respirator example, for which the null hypothesis is H 0 : μ = 75 , the claim that the average time air is delivered for all respirators is 75 minutes. If the sample mean is 75 or greater then we certainly would not reject H 0 (since there is no issue with an emergency respirator delivering air even longer than claimed).

If the sample mean is slightly less than 75 then we would logically attribute the difference to sampling error and also not reject H 0 either.

Values of the sample mean that are smaller and smaller are less and less likely to come from a population for which the population mean is 75. Thus if the sample mean is far less than 75, say around 60 minutes or less, then we would certainly reject H 0 , because we know that it is highly unlikely that the average of a sample would be so low if the population mean were 75. This is the rare event criterion for rejection: what we actually observed ( X - < 60 ) would be so rare an event if μ = 75 were true that we regard it as much more likely that the alternative hypothesis μ < 75 holds.

In summary, to decide between H 0 and H a in this example we would select a “ rejection region An interval or union of intervals such that the null hypothesis is rejected if and only if the statistic of interest lies in this region. ” of values sufficiently far to the left of 75, based on the rare event criterion, and reject H 0 if the sample mean X - lies in the rejection region, but not reject H 0 if it does not.

The Rejection Region

Each different form of the alternative hypothesis H a has its own kind of rejection region:

• if (as in the respirator example) H a has the form H a : μ < μ 0 , we reject H 0 if x - is far to the left of μ 0 , that is, to the left of some number C , so the rejection region has the form of an interval (−∞, C ];
• if (as in the textbook example) H a has the form H a : μ > μ 0 , we reject H 0 if x - is far to the right of μ 0 , that is, to the right of some number C , so the rejection region has the form of an interval [ C ,∞);
• if (as in the baked good example) H a has the form H a : μ ≠ μ 0 , we reject H 0 if x - is far away from μ 0 in either direction, that is, either to the left of some number C or to the right of some other number C ′, so the rejection region has the form of the union of two intervals (−∞, C ]∪[ C ′,∞).

The key issue in our line of reasoning is the question of how to determine the number C or numbers C and C ′, called the critical value or critical values of the statistic, that determine the rejection region.

The critical value The number or one of a pair of numbers that determines the rejection region. or critical values of a test of hypotheses are the number or numbers that determine the rejection region.

Suppose the rejection region is a single interval, so we need to select a single number C . Here is the procedure for doing so. We select a small probability, denoted α , say 1%, which we take as our definition of “rare event:” an event is “rare” if its probability of occurrence is less than α . (In all the examples and problems in this text the value of α will be given already.) The probability that X - takes a value in an interval is the area under its density curve and above that interval, so as shown in Figure 8.2 (drawn under the assumption that H 0 is true, so that the curve centers at μ 0 ) the critical value C is the value of X - that cuts off a tail area α in the probability density curve of X - . When the rejection region is in two pieces, that is, composed of two intervals, the total area above both of them must be α , so the area above each one is α ∕ 2 , as also shown in Figure 8.2 .

The number α is the total area of a tail or a pair of tails.

In the context of Note 8.9 "Example 2" , suppose that it is known that the population is normally distributed with standard deviation σ = 0.15 gram, and suppose that the test of hypotheses H 0 : μ = 8.0 versus H a : μ ≠ 8.0 will be performed with a sample of size 5. Construct the rejection region for the test for the choice α = 0.10 . Explain the decision procedure and interpret it.

If H 0 is true then the sample mean X - is normally distributed with mean and standard deviation

Since H a contains the ≠ symbol the rejection region will be in two pieces, each one corresponding to a tail of area α ∕ 2 = 0.10 ∕ 2 = 0.05 . From Figure 12.3 "Critical Values of " , z 0.05 = 1.645 , so C and C ′ are 1.645 standard deviations of X - to the right and left of its mean 8.0:

The result is shown in Figure 8.3 "Rejection Region for the Choice " .

Figure 8.3 Rejection Region for the Choice α = 0.10

The decision procedure is: take a sample of size 5 and compute the sample mean x - . If x - is either 7.89 grams or less or 8.11 grams or more then reject the hypothesis that the average amount of fat in all servings of the product is 8.0 grams in favor of the alternative that it is different from 8.0 grams. Otherwise do not reject the hypothesis that the average amount is 8.0 grams.

The reasoning is that if the true average amount of fat per serving were 8.0 grams then there would be less than a 10% chance that a sample of size 5 would produce a mean of either 7.89 grams or less or 8.11 grams or more. Hence if that happened it would be more likely that the value 8.0 is incorrect (always assuming that the population standard deviation is 0.15 gram).

Because the rejection regions are computed based on areas in tails of distributions, as shown in Figure 8.2 , hypothesis tests are classified according to the form of the alternative hypothesis in the following way.

If H a has the form μ ≠ μ 0 the test is called a two-tailed test .

If H a has the form μ < μ 0 the test is called a left-tailed test .

If H a has the form μ > μ 0 the test is called a right-tailed test .

Each of the last two forms is also called a one-tailed test .

Two Types of Errors

The format of the testing procedure in general terms is to take a sample and use the information it contains to come to a decision about the two hypotheses. As stated before our decision will always be either

• reject the null hypothesis H 0 in favor of the alternative H a presented, or
• do not reject the null hypothesis H 0 in favor of the alternative H a presented.

There are four possible outcomes of hypothesis testing procedure, as shown in the following table:

As the table shows, there are two ways to be right and two ways to be wrong. Typically to reject H 0 when it is actually true is a more serious error than to fail to reject it when it is false, so the former error is labeled “Type I” and the latter error “Type II.”

In a test of hypotheses, a Type I error Rejection of a true null hypothesis. is the decision to reject H 0 when it is in fact true. A Type II error Failure to reject a false null hypothesis. is the decision not to reject H 0 when it is in fact not true.

Unless we perform a census we do not have certain knowledge, so we do not know whether our decision matches the true state of nature or if we have made an error. We reject H 0 if what we observe would be a “rare” event if H 0 were true. But rare events are not impossible: they occur with probability α . Thus when H 0 is true, a rare event will be observed in the proportion α of repeated similar tests, and H 0 will be erroneously rejected in those tests. Thus α is the probability that in following the testing procedure to decide between H 0 and H a we will make a Type I error.

The number α that is used to determine the rejection region is called the level of significance of the test The probability α that defines an event as “rare;” the probability that the test procedure will lead to a Type I error. . It is the probability that the test procedure will result in a Type I error.

The probability of making a Type II error is too complicated to discuss in a beginning text, so we will say no more about it than this: for a fixed sample size, choosing α smaller in order to reduce the chance of making a Type I error has the effect of increasing the chance of making a Type II error. The only way to simultaneously reduce the chances of making either kind of error is to increase the sample size.

Standardizing the Test Statistic

Hypotheses testing will be considered in a number of contexts, and great unification as well as simplification results when the relevant sample statistic is standardized by subtracting its mean from it and then dividing by its standard deviation. The resulting statistic is called a standardized test statistic . In every situation treated in this and the following two chapters the standardized test statistic will have either the standard normal distribution or Student’s t -distribution.

A standardized test statistic The standardized statistic used in performing the test. for a hypothesis test is the statistic that is formed by subtracting from the statistic of interest its mean and dividing by its standard deviation.

For example, reviewing Note 8.14 "Example 3" , if instead of working with the sample mean X - we instead work with the test statistic

then the distribution involved is standard normal and the critical values are just ± z 0.05 . The extra work that was done to find that C = 7.89 and C ′ = 8.11 is eliminated. In every hypothesis test in this book the standardized test statistic will be governed by either the standard normal distribution or Student’s t -distribution. Information about rejection regions is summarized in the following tables:

Every instance of hypothesis testing discussed in this and the following two chapters will have a rejection region like one of the six forms tabulated in the tables above.

No matter what the context a test of hypotheses can always be performed by applying the following systematic procedure, which will be illustrated in the examples in the succeeding sections.

Systematic Hypothesis Testing Procedure: Critical Value Approach

• Identify the null and alternative hypotheses.
• Identify the relevant test statistic and its distribution.
• Compute from the data the value of the test statistic.
• Construct the rejection region.
• Compare the value computed in Step 3 to the rejection region constructed in Step 4 and make a decision. Formulate the decision in the context of the problem, if applicable.

The procedure that we have outlined in this section is called the “Critical Value Approach” to hypothesis testing to distinguish it from an alternative but equivalent approach that will be introduced at the end of Section 8.3 "The Observed Significance of a Test" .

Key Takeaways

• A test of hypotheses is a statistical process for deciding between two competing assertions about a population parameter.
• The testing procedure is formalized in a five-step procedure.

State the null and alternative hypotheses for each of the following situations. (That is, identify the correct number μ 0 and write H 0 : μ = μ 0 and the appropriate analogous expression for H a .)

• The average July temperature in a region historically has been 74.5°F. Perhaps it is higher now.
• The average weight of a female airline passenger with luggage was 145 pounds ten years ago. The FAA believes it to be higher now.
• The average stipend for doctoral students in a particular discipline at a state university is $14,756. The department chairman believes that the national average is higher.
• The average room rate in hotels in a certain region is $82.53. A travel agent believes that the average in a particular resort area is different.
• The average farm size in a predominately rural state was 69.4 acres. The secretary of agriculture of that state asserts that it is less today.
• The average time workers spent commuting to work in Verona five years ago was 38.2 minutes. The Verona Chamber of Commerce asserts that the average is less now.
• The mean salary for all men in a certain profession is $58,291. A special interest group thinks that the mean salary for women in the same profession is different.
• The accepted figure for the caffeine content of an 8-ounce cup of coffee is 133 mg. A dietitian believes that the average for coffee served in a local restaurants is higher.
• The average yield per acre for all types of corn in a recent year was 161.9 bushels. An economist believes that the average yield per acre is different this year.
• An industry association asserts that the average age of all self-described fly fishermen is 42.8 years. A sociologist suspects that it is higher.

Describe the two types of errors that can be made in a test of hypotheses.

Under what circumstance is a test of hypotheses certain to yield a correct decision?

• H 0 : μ = 74.5 vs. H a : μ > 74.5
• H 0 : μ = 145 vs. H a : μ > 145
• H 0 : μ = 14756 vs. H a : μ > 14756
• H 0 : μ = 82.53 vs. H a : μ ≠ 82.53
• H 0 : μ = 69.4 vs. H a : μ < 69.4

A Type I error is made when a true H 0 is rejected. A Type II error is made when a false H 0 is not rejected.

Statistics Made Easy

How to Write Hypothesis Test Conclusions (With Examples)

A   hypothesis test is used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we reject the null hypothesis .

Otherwise, if the p-value is not less than some significance level then we fail to reject the null hypothesis .

When writing the conclusion of a hypothesis test, we typically include:

• Whether we reject or fail to reject the null hypothesis.
• The significance level.
• A short explanation in the context of the hypothesis test.

For example, we would write:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that…

Or, we would write:

We fail to reject the null hypothesis at the 5% significance level.   There is not sufficient evidence to support the claim that…

The following examples show how to write a hypothesis test conclusion in both scenarios.

Example 1: Reject the Null Hypothesis Conclusion

Suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test at a 5% significance level using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

Suppose the p-value of the test turns out to be 0.002.

Here is how she would report the results of the hypothesis test:

We reject the null hypothesis at the 5% significance level.   There is sufficient evidence to support the claim that this particular fertilizer causes plants to grow more during a one-month period than they normally do.

Example 2: Fail to Reject the Null Hypothesis Conclusion

Suppose the manager of a manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, he measures the mean number of defective widgets produced before and after using the new method for one month.

He performs a hypothesis test at a 10% significance level using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

Suppose the p-value of the test turns out to be 0.27.

Here is how he would report the results of the hypothesis test:

We fail to reject the null hypothesis at the 10% significance level.   There is not sufficient evidence to support the claim that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

The following tutorials provide additional information about hypothesis testing:

Introduction to Hypothesis Testing 4 Examples of Hypothesis Testing in Real Life How to Write a Null Hypothesis

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6a.2 - steps for hypothesis tests, the logic of hypothesis testing section  .

A hypothesis, in statistics, is a statement about a population parameter, where this statement typically is represented by some specific numerical value. In testing a hypothesis, we use a method where we gather data in an effort to gather evidence about the hypothesis.

How do we decide whether to reject the null hypothesis?

• If the sample data are consistent with the null hypothesis, then we do not reject it.
• If the sample data are inconsistent with the null hypothesis, but consistent with the alternative, then we reject the null hypothesis and conclude that the alternative hypothesis is true.

Six Steps for Hypothesis Tests Section  

In hypothesis testing, there are certain steps one must follow. Below these are summarized into six such steps to conducting a test of a hypothesis.

• Set up the hypotheses and check conditions : Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as \(H_0 \), which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is evidence to suggest otherwise. The second hypothesis is called the alternative, or research hypothesis, notated as \(H_a \). The alternative hypothesis is a statement of a range of alternative values in which the parameter may fall. One must also check that any conditions (assumptions) needed to run the test have been satisfied e.g. normality of data, independence, and number of success and failure outcomes.
• Decide on the significance level, \(\alpha \): This value is used as a probability cutoff for making decisions about the null hypothesis. This alpha value represents the probability we are willing to place on our test for making an incorrect decision in regards to rejecting the null hypothesis. The most common \(\alpha \) value is 0.05 or 5%. Other popular choices are 0.01 (1%) and 0.1 (10%).
• Calculate the test statistic: Gather sample data and calculate a test statistic where the sample statistic is compared to the parameter value. The test statistic is calculated under the assumption the null hypothesis is true and incorporates a measure of standard error and assumptions (conditions) related to the sampling distribution.
• Calculate probability value (p-value), or find the rejection region: A p-value is found by using the test statistic to calculate the probability of the sample data producing such a test statistic or one more extreme. The rejection region is found by using alpha to find a critical value; the rejection region is the area that is more extreme than the critical value. We discuss the p-value and rejection region in more detail in the next section.
• Make a decision about the null hypothesis: In this step, we decide to either reject the null hypothesis or decide to fail to reject the null hypothesis. Notice we do not make a decision where we will accept the null hypothesis.
• State an overall conclusion : Once we have found the p-value or rejection region, and made a statistical decision about the null hypothesis (i.e. we will reject the null or fail to reject the null), we then want to summarize our results into an overall conclusion for our test.

We will follow these six steps for the remainder of this Lesson. In the future Lessons, the steps will be followed but may not be explained explicitly.

Step 1 is a very important step to set up correctly. If your hypotheses are incorrect, your conclusion will be incorrect. In this next section, we practice with Step 1 for the one sample situations.

In-class problems on hypothesis tests  

Decide whether the following statements are true or false.  Explain your reasoning.

a)  A p-value of .08 is more evidence against the null hypothesis than a p-value of .04.

False.  A small p-value means the value of the statistic we observed in the sample is unlikely to have occurred when the null hypothesis is true.  Hence, a .04 p-value means it is even more unlikely the observed statistic would have occurred when the null hypothesis is true than a .08 p-value.   The smaller the p-value, the stronger the evidence against the null hypothesis.

b)  If two independent studies are done on the same population with the purpose of testing the same hypotheses, the study with the larger sample size is more likely to have a smaller p-value than the study with the smaller sample size.  (Hint:  Consider if this is true in the case of the null hypothesis is true and in the case of the null hypothesis is false.)

By definition, p-values take into consideration the sample size, since the test statistic has the standard error in the denominator.  Hence, when the null hypothesis is true, a small p-value should be equally likely regardless of sample size.  However, when the null hypothesis is false, hypothesis tests done with large sample sizes are more likely to reveal the false null, and hence more likely to result in a small p-value.

False.   The null hypothesis is either true, or it is not true.  Hence, the probability that it is true equals either zero or one.  The p-value is not interpreted as a probability that the null hypothesis is true.   It is the probability of observing a value of the test statistic that is as or more extreme than what was observed in the sample, assuming the null hypothesis is true. 

True.  Just by chance it is possible to get a sample that produces a small p-value, even though the null hypothesis is true.  This is called a Type I error.   A Type II error is when the null hypothesis is not rejected when it is in fact false.

By valid, we mean that the p-value is an accurate summary of the evidence against the null hypothesis. False.  The central limit theorem is needed for hypothesis tests to be valid.   However, it is also necessary that the data be collected from random samples.  Hypothesis tests will not remedy poorly collected data.

False.  The researcher is claiming that (1 - p-value) is the probability that the alternative hypothesis is false.  The p-value is not a probability of an alternative (or null) hypothesis being true or false.  See the answer to part c.

h)  You are the head of the Food and Drug Administration (F.D.A.), in charge of deciding whether new drugs are effective and should be allowed to be sold to people.   A pharmaceutical company trying to win approval for a new drug they manufacture claims that their drug is better than the standard drug at curing a certain disease.   The company bases this claim on a study in which they gave their drug to 1000 volunteers with the disease.   They compared these volunteers to a group of 1000 hospital patients who were treated with the standard drug and whose information is obtained from existing hospital records.  The company found a "statistically significant" difference between the percentage of volunteers who were cured and the percentage of the comparison group who were cured.   That is, they did a statistical hypothesis test and rejected the null hypothesis that the percentages are equal.  As director of the F.D.A., should you permit the new drug to be sold?  Explain your reasoning in three or less sentences.

You should not allow the drug to be manufactured based on this evidence.  The study was not a randomized study, which means there may be differences in the background charcteristics of the people who got the new drug and the people who got the old drug.   Hypothesis tests cannot fix poorly designed studies.

i)  If you get a p-value of 0.13, it means there is a 13% chance that the sample average equals the population average.

False.  In fact, it's almost guaranteed that the sample average won't exactly equal the population average, because the process of taking a random sample guarantees variability in the sample average.  The p-value does not give the probability that the sample average equals the population average.   See part c for the precise definition of p-values. j)  If you get a p-value of 0.13, it means there is a 13% chance that the sample average does not equal the population average.

False.  See the answer to part i. k)  If you get a p-value of 0.13, it means there is an 87% chance that the sample average equals the population average.

False.  Computing (1 - p-value) does not give the probability that the sample average equals the population average. See the answer to part i.

l)  If you get a p-value of 0.13, it means there is an 87% chance that the sample average does not equal the population average.

False.  See the answer to part k.

m)  If you get a p-value of 0.13, it means that the null hypothesis is true in 13% of all samples.

False.  The null hypothesis is either true or false.  Truth does not change with different samples, only the test statistic (which is based on sample means and SEs) changes with different samples.

n)  If you get a p-value of 0.13, it means that when the null hypothesis is true, a value of the test statistic as or more extreme than what was observed occurs in about 13% of all samples.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: The Fundamentals of Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 2883

• Diane Kiernan
• SUNY College of Environmental Science and Forestry via OpenSUNY

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The previous two chapters introduced methods for organizing and summarizing sample data, and using sample statistics to estimate population parameters. This chapter introduces the next major topic of inferential statistics: hypothesis testing.

A hypothesis is a statement or claim about a property of a population.

The Fundamentals of Hypothesis Testing

When conducting scientific research, typically there is some known information, perhaps from some past work or from a long accepted idea. We want to test whether this claim is believable. This is the basic idea behind a hypothesis test:

• State what we think is true.
• Quantify how confident we are about our claim.
• Use sample statistics to make inferences about population parameters.

For example, past research tells us that the average life span for a hummingbird is about four years. You have been studying the hummingbirds in the southeastern United States and find a sample mean lifespan of 4.8 years. Should you reject the known or accepted information in favor of your results? How confident are you in your estimate? At what point would you say that there is enough evidence to reject the known information and support your alternative claim? How far from the known mean of four years can the sample mean be before we reject the idea that the average lifespan of a hummingbird is four years?

Definition: hypothesis testing

Hypothesis testing is a procedure, based on sample evidence and probability, used to test claims regarding a characteristic of a population.

A hypothesis is a claim or statement about a characteristic of a population of interest to us. A hypothesis test is a way for us to use our sample statistics to test a specific claim.

Example \(\PageIndex{1}\):

The population mean weight is known to be 157 lb. We want to test the claim that the mean weight has increased.

Example \(\PageIndex{2}\):

Two years ago, the proportion of infected plants was 37%. We believe that a treatment has helped, and we want to test the claim that there has been a reduction in the proportion of infected plants.

Components of a Formal Hypothesis Test

The null hypothesis is a statement about the value of a population parameter, such as the population mean (µ) or the population proportion ( p ). It contains the condition of equality and is denoted as H 0 (H-naught).

H 0 : µ = 157 or H0 : p = 0.37

The alternative hypothesis is the claim to be tested, the opposite of the null hypothesis. It contains the value of the parameter that we consider plausible and is denoted as H 1 .

H 1 : µ > 157 or H1 : p ≠ 0.37

The test statistic is a value computed from the sample data that is used in making a decision about the rejection of the null hypothesis. The test statistic converts the sample mean ( x̄ ) or sample proportion ( p̂ ) to a Z- or t-score under the assumption that the null hypothesis is true. It is used to decide whether the difference between the sample statistic and the hypothesized claim is significant.

The p-value is the area under the curve to the left or right of the test statistic. It is compared to the level of significance (α).

The critical value is the value that defines the rejection zone (the test statistic values that would lead to rejection of the null hypothesis). It is defined by the level of significance.

The level of significance (α) is the probability that the test statistic will fall into the critical region when the null hypothesis is true. This level is set by the researcher.

The conclusion is the final decision of the hypothesis test. The conclusion must always be clearly stated, communicating the decision based on the components of the test. It is important to realize that we never prove or accept the null hypothesis. We are merely saying that the sample evidence is not strong enough to warrant the rejection of the null hypothesis. The conclusion is made up of two parts:

1) Reject or fail to reject the null hypothesis, and 2) there is or is not enough evidence to support the alternative claim.

Option 1) Reject the null hypothesis (H0). This means that you have enough statistical evidence to support the alternative claim (H 1 ).

Option 2) Fail to reject the null hypothesis (H0). This means that you do NOT have enough evidence to support the alternative claim (H 1 ).

Another way to think about hypothesis testing is to compare it to the US justice system. A defendant is innocent until proven guilty (Null hypothesis—innocent). The prosecuting attorney tries to prove that the defendant is guilty (Alternative hypothesis—guilty). There are two possible conclusions that the jury can reach. First, the defendant is guilty (Reject the null hypothesis). Second, the defendant is not guilty (Fail to reject the null hypothesis). This is NOT the same thing as saying the defendant is innocent! In the first case, the prosecutor had enough evidence to reject the null hypothesis (innocent) and support the alternative claim (guilty). In the second case, the prosecutor did NOT have enough evidence to reject the null hypothesis (innocent) and support the alternative claim of guilty.

The Null and Alternative Hypotheses

There are three different pairs of null and alternative hypotheses:

Table \(PageIndex{1}\): The rejection zone for a two-sided hypothesis test.

where c is some known value.

A Two-sided Test

This tests whether the population parameter is equal to, versus not equal to, some specific value.

Ho: μ = 12 vs. H 1 : μ ≠ 12

The critical region is divided equally into the two tails and the critical values are ± values that define the rejection zones.

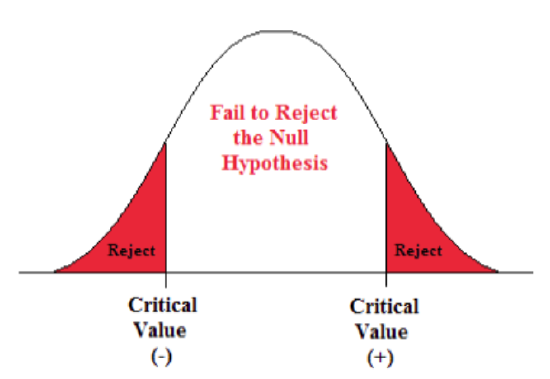
Example \(\PageIndex{3}\):

A forester studying diameter growth of red pine believes that the mean diameter growth will be different if a fertilization treatment is applied to the stand.

• Ho: μ = 1.2 in./ year
• H 1 : μ ≠ 1.2 in./ year

This is a two-sided question, as the forester doesn’t state whether population mean diameter growth will increase or decrease.

A Right-sided Test

This tests whether the population parameter is equal to, versus greater than, some specific value.

Ho: μ = 12 vs. H 1 : μ > 12

The critical region is in the right tail and the critical value is a positive value that defines the rejection zone.

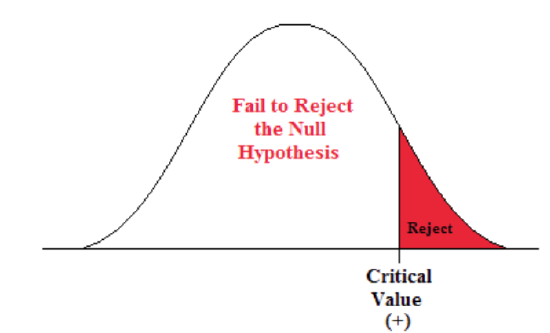
Example \(\PageIndex{4}\):

A biologist believes that there has been an increase in the mean number of lakes infected with milfoil, an invasive species, since the last study five years ago.

• Ho: μ = 15 lakes
• H1: μ >15 lakes

This is a right-sided question, as the biologist believes that there has been an increase in population mean number of infected lakes.

A Left-sided Test

This tests whether the population parameter is equal to, versus less than, some specific value.

Ho: μ = 12 vs. H 1 : μ < 12

The critical region is in the left tail and the critical value is a negative value that defines the rejection zone.

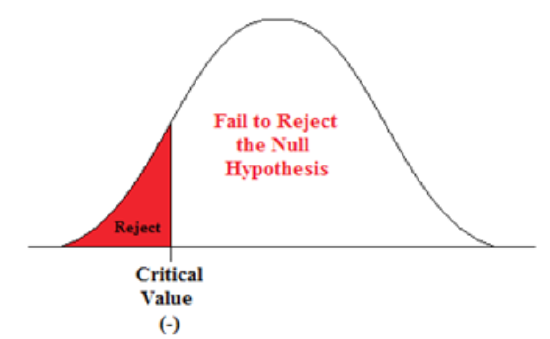
Example \(\PageIndex{5}\):

A scientist’s research indicates that there has been a change in the proportion of people who support certain environmental policies. He wants to test the claim that there has been a reduction in the proportion of people who support these policies.

• Ho: p = 0.57
• H 1 : p < 0.57

This is a left-sided question, as the scientist believes that there has been a reduction in the true population proportion.

Statistically Significant

When the observed results (the sample statistics) are unlikely (a low probability) under the assumption that the null hypothesis is true, we say that the result is statistically significant, and we reject the null hypothesis. This result depends on the level of significance, the sample statistic, sample size, and whether it is a one- or two-sided alternative hypothesis.

Types of Errors

When testing, we arrive at a conclusion of rejecting the null hypothesis or failing to reject the null hypothesis. Such conclusions are sometimes correct and sometimes incorrect (even when we have followed all the correct procedures). We use incomplete sample data to reach a conclusion and there is always the possibility of reaching the wrong conclusion. There are four possible conclusions to reach from hypothesis testing. Of the four possible outcomes, two are correct and two are NOT correct.

Table \(\PageIndex{2}\). Possible outcomes from a hypothesis test.

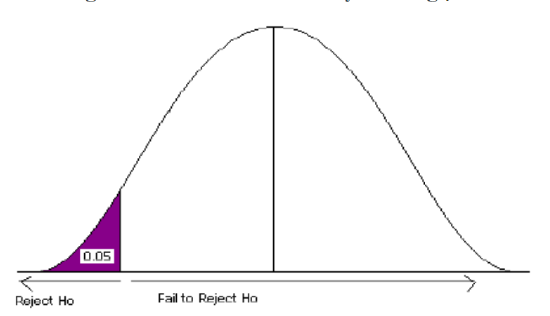
A Type I error is when we reject the null hypothesis when it is true. The symbol α (alpha) is used to represent Type I errors. This is the same alpha we use as the level of significance. By setting alpha as low as reasonably possible, we try to control the Type I error through the level of significance.

A Type II error is when we fail to reject the null hypothesis when it is false. The symbol β(beta) is used to represent Type II errors.

In general, Type I errors are considered more serious. One step in the hypothesis test procedure involves selecting the significance level ( α ), which is the probability of rejecting the null hypothesis when it is correct. So the researcher can select the level of significance that minimizes Type I errors. However, there is a mathematical relationship between α, β, and n (sample size).

• As α increases, β decreases
• As α decreases, β increases
• As sample size increases (n), both α and β decrease

The natural inclination is to select the smallest possible value for α, thinking to minimize the possibility of causing a Type I error. Unfortunately, this forces an increase in Type II errors. By making the rejection zone too small, you may fail to reject the null hypothesis, when, in fact, it is false. Typically, we select the best sample size and level of significance, automatically setting β.

Power of the Test

A Type II error (β) is the probability of failing to reject a false null hypothesis. It follows that 1-β is the probability of rejecting a false null hypothesis. This probability is identified as the power of the test, and is often used to gauge the test’s effectiveness in recognizing that a null hypothesis is false.

Definition: power of the test

The probability that at a fixed level α significance test will reject H0, when a particular alternative value of the parameter is true is called the power of the test.

Power is also directly linked to sample size. For example, suppose the null hypothesis is that the mean fish weight is 8.7 lb. Given sample data, a level of significance of 5%, and an alternative weight of 9.2 lb., we can compute the power of the test to reject μ = 8.7 lb. If we have a small sample size, the power will be low. However, increasing the sample size will increase the power of the test. Increasing the level of significance will also increase power. A 5% test of significance will have a greater chance of rejecting the null hypothesis than a 1% test because the strength of evidence required for the rejection is less. Decreasing the standard deviation has the same effect as increasing the sample size: there is more information about μ.