- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Unlocking the Power of Advanced Statistical Methods in Clinical Trials

Mastering Statistical Power and Sample Size Determination
Explaining hypothesis testing with real-world examples.

Hypothesis testing is a fundamental concept in statistics, particularly in the field of medical research. At StatisMed, we understand the importance of accurately analyzing data to draw meaningful conclusions. In this blog post, we get insights into explaining hypothesis testing with real-world examples and how it can be applied in medical settings.
Understanding Hypothesis Testing
Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating a null hypothesis (H0) and an alternative hypothesis (H1), collecting data, performing statistical tests, and drawing conclusions based on the results.
Real-World Examples
- A pharmaceutical company wants to test a new drug’s effectiveness in lowering blood pressure compared to the current standard treatment. The null hypothesis states that there is no difference in blood pressure reduction between the two treatments, while the alternative hypothesis suggests that the new drug is more effective.
- Researches conducting a clinical trial to determine the efficacy of a new vaccine in preventing a specific disease. The null hypothesis posits that the vaccine does not provide any protection, while the alternative hypothesis proposes that the vaccine is effective.
- A medical team wants to compare the effectiveness of two treatments for a certain condition. By formulating null and alternative hypotheses, collecting data on patient outcomes, and performing statistical tests, they can determine which treatment is more effective.
Application in Medical Research
In the field of medical research, hypothesis testing plays a crucial role in evaluating new treatments, determining the effectiveness of interventions, and establishing evidence-based practices. By using statistical analysis services from StatisMed, medical professionals can ensure their research is conducted rigorously and ethically.
Hypothesis testing is a powerful tool that allows researchers to draw meaningful conclusions from data. By explaining hypothesis testing with real-world examples and applying them in real-world scenarios, medical professionals can make informed decisions about treatment options, interventions, and research outcomes. At StatisMed, we are committed to providing top-notch statistical analysis services to support evidence-based medical research. Contact us to learn more about how we can assist you in unlocking the potential of hypothesis testing in your research projects.
Related Articles

- Uncategorized
Understanding Bayesian Inference
Exploring the Characteristics of Normal Distribution

Top Medical Research Studies That Pay Participants

- Research article
- Open access
- Published: 19 May 2010
The null hypothesis significance test in health sciences research (1995-2006): statistical analysis and interpretation
- Luis Carlos Silva-Ayçaguer 1 ,
- Patricio Suárez-Gil 2 &
- Ana Fernández-Somoano 3
BMC Medical Research Methodology volume 10 , Article number: 44 ( 2010 ) Cite this article
38k Accesses
23 Citations
18 Altmetric
Metrics details
The null hypothesis significance test (NHST) is the most frequently used statistical method, although its inferential validity has been widely criticized since its introduction. In 1988, the International Committee of Medical Journal Editors (ICMJE) warned against sole reliance on NHST to substantiate study conclusions and suggested supplementary use of confidence intervals (CI). Our objective was to evaluate the extent and quality in the use of NHST and CI, both in English and Spanish language biomedical publications between 1995 and 2006, taking into account the International Committee of Medical Journal Editors recommendations, with particular focus on the accuracy of the interpretation of statistical significance and the validity of conclusions.
Original articles published in three English and three Spanish biomedical journals in three fields (General Medicine, Clinical Specialties and Epidemiology - Public Health) were considered for this study. Papers published in 1995-1996, 2000-2001, and 2005-2006 were selected through a systematic sampling method. After excluding the purely descriptive and theoretical articles, analytic studies were evaluated for their use of NHST with P-values and/or CI for interpretation of statistical "significance" and "relevance" in study conclusions.
Among 1,043 original papers, 874 were selected for detailed review. The exclusive use of P-values was less frequent in English language publications as well as in Public Health journals; overall such use decreased from 41% in 1995-1996 to 21% in 2005-2006. While the use of CI increased over time, the "significance fallacy" (to equate statistical and substantive significance) appeared very often, mainly in journals devoted to clinical specialties (81%). In papers originally written in English and Spanish, 15% and 10%, respectively, mentioned statistical significance in their conclusions.
Conclusions
Overall, results of our review show some improvements in statistical management of statistical results, but further efforts by scholars and journal editors are clearly required to move the communication toward ICMJE advices, especially in the clinical setting, which seems to be imperative among publications in Spanish.
Peer Review reports
The null hypothesis statistical testing (NHST) has been the most widely used statistical approach in health research over the past 80 years. Its origins dates back to 1279 [ 1 ] although it was in the second decade of the twentieth century when the statistician Ronald Fisher formally introduced the concept of "null hypothesis" H 0 - which, generally speaking, establishes that certain parameters do not differ from each other. He was the inventor of the "P-value" through which it could be assessed [ 2 ]. Fisher's P-value is defined as a conditional probability calculated using the results of a study. Specifically, the P-value is the probability of obtaining a result at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. The Fisherian significance testing theory considered the p-value as an index to measure the strength of evidence against the null hypothesis in a single experiment. The father of NHST never endorsed, however, the inflexible application of the ultimately subjective threshold levels almost universally adopted later on (although the introduction of the 0.05 has his paternity also).
A few years later, Jerzy Neyman and Egon Pearson considered the Fisherian approach inefficient, and in 1928 they published an article [ 3 ] that would provide the theoretical basis of what they called hypothesis statistical testing . The Neyman-Pearson approach is based on the notion that one out of two choices has to be taken: accept the null hypothesis taking the information as a reference based on the information provided, or reject it in favor of an alternative one. Thus, one can incur one of two types of errors: a Type I error, if the null hypothesis is rejected when it is actually true, and a Type II error, if the null hypothesis is accepted when it is actually false. They established a rule to optimize the decision process, using the p-value introduced by Fisher, by setting the maximum frequency of errors that would be admissible.
The null hypothesis statistical testing, as applied today, is a hybrid coming from the amalgamation of the two methods [ 4 ]. As a matter of fact, some 15 years later, both procedures were combined to give rise to the nowadays widespread use of an inferential tool that would satisfy none of the statisticians involved in the original controversy. The present method essentially goes as follows: given a null hypothesis, an estimate of the parameter (or parameters) is obtained and used to create statistics whose distribution, under H 0 , is known. With these data the P-value is computed. Finally, the null hypothesis is rejected when the obtained P-value is smaller than a certain comparative threshold (usually 0.05) and it is not rejected if P is larger than the threshold.
The first reservations about the validity of the method began to appear around 1940, when some statisticians censured the logical roots and practical convenience of Fisher's P-value [ 5 ]. Significance tests and P-values have repeatedly drawn the attention and criticism of many authors over the past 70 years, who have kept questioning its epistemological legitimacy as well as its practical value. What remains in spite of these criticisms is the lasting legacy of researchers' unwillingness to eradicate or reform these methods.
Although there are very comprehensive works on the topic [ 6 ], we list below some of the criticisms most universally accepted by specialists.
The P-values are used as a tool to make decisions in favor of or against a hypothesis. What really may be relevant, however, is to get an effect size estimate (often the difference between two values) rather than rendering dichotomous true/false verdicts [ 7 – 11 ].
The P-value is a conditional probability of the data, provided that some assumptions are met, but what really interests the investigator is the inverse probability: what degree of validity can be attributed to each of several competing hypotheses, once that certain data have been observed [ 12 ].
The two elements that affect the results, namely the sample size and the magnitude of the effect, are inextricably linked in the value of p and we can always get a lower P-value by increasing the sample size. Thus, the conclusions depend on a factor completely unrelated to the reality studied (i.e. the available resources, which in turn determine the sample size) [ 13 , 14 ].
Those who defend the NHST often assert the objective nature of that test, but the process is actually far from being so. NHST does not ensure objectivity. This is reflected in the fact that we generally operate with thresholds that are ultimately no more than conventions, such as 0.01 or 0.05. What is more, for many years their use has unequivocally demonstrated the inherent subjectivity that goes with the concept of P, regardless of how it will be used later [ 15 – 17 ].
In practice, the NHST is limited to a binary response sorting hypotheses into "true" and "false" or declaring "rejection" or "no rejection", without demanding a reasonable interpretation of the results, as has been noted time and again for decades. This binary orthodoxy validates categorical thinking, which results in a very simplistic view of scientific activity that induces researchers not to test theories about the magnitude of effect sizes [ 18 – 20 ].
Despite the weakness and shortcomings of the NHST, they are frequently taught as if they were the key inferential statistical method or the most appropriate, or even the sole unquestioned one. The statistical textbooks, with only some exceptions, do not even mention the NHST controversy. Instead, the myth is spread that NHST is the "natural" final action of scientific inference and the only procedure for testing hypotheses. However, relevant specialists and important regulators of the scientific world advocate avoiding them.
Taking especially into account that NHST does not offer the most important information (i.e. the magnitude of an effect of interest, and the precision of the estimate of the magnitude of that effect), many experts recommend the reporting of point estimates of effect sizes with confidence intervals as the appropriate representation of the inherent uncertainty linked to empirical studies [ 21 – 25 ]. Since 1988, the International Committee of Medical Journal Editors (ICMJE, known as the Vancouver Group ) incorporates the following recommendation to authors of manuscripts submitted to medical journals: "When possible, quantify findings and present them with appropriate indicators of measurement error or uncertainty (such as confidence intervals). Avoid relying solely on statistical hypothesis testing, such as P-values, which fail to convey important information about effect size" [ 26 ].
As will be shown, the use of confidence intervals (CI), occasionally accompanied by P-values, is recommended as a more appropriate method for reporting results. Some authors have noted several shortcomings of CI long ago [ 27 ]. In spite of the fact that calculating CI could be complicated indeed, and that their interpretation is far from simple [ 28 , 29 ], authors are urged to use them because they provide much more information than the NHST and do not merit most of its criticisms of NHST [ 30 ]. While some have proposed different options (for instance, likelihood-based information theoretic methods [ 31 ], and the Bayesian inferential paradigm [ 32 ]), confidence interval estimation of effect sizes is clearly the most widespread alternative approach.
Although twenty years have passed since the ICMJE began to disseminate such recommendations, systematically ignored by the vast majority of textbooks and hardly incorporated in medical publications [ 33 ], it is interesting to examine the extent to which the NHST is used in articles published in medical journals during recent years, in order to identify what is still lacking in the process of eradicating the widespread ceremonial use that is made of statistics in health research [ 34 ]. Furthermore, it is enlightening in this context to examine whether these patterns differ between English- and Spanish-speaking worlds and, if so, to see if the changes in paradigms are occurring more slowly in Spanish-language publications. In such a case we would offer various suggestions.
In addition to assessing the adherence to the above cited statistical recommendation proposed by ICMJE relative to the use of P-values, we consider it of particular interest to estimate the extent to which the significance fallacy is present, an inertial deficiency that consists of attributing -- explicitly or not -- qualitative importance or practical relevance to the found differences simply because statistical significance was obtained.
Many authors produce misleading statements such as "a significant effect was (or was not) found" when it should be said that "a statistically significant difference was (or was not) found". A detrimental consequence of this equivalence is that some authors believe that finding out whether there is "statistical significance" or not is the aim, so that this term is then mentioned in the conclusions [ 35 ]. This means virtually nothing, except that it indicates that the author is letting a computer do the thinking. Since the real research questions are never statistical ones, the answers cannot be statistical either. Accordingly, the conversion of the dichotomous outcome produced by a NHST into a conclusion is another manifestation of the mentioned fallacy.
The general objective of the present study is to evaluate the extent and quality of use of NHST and CI, both in English- and in Spanish-language biomedical publications, between 1995 and 2006 taking into account the International Committee of Medical Journal Editors recommendations, with particular focus on accuracy regarding interpretation of statistical significance and the validity of conclusions.
We reviewed the original articles from six journals, three in English and three in Spanish, over three disjoint periods sufficiently separated from each other (1995-1996, 2000-2001, 2005-2006) as to properly describe the evolution in prevalence of the target features along the selected periods.
The selection of journals was intended to get representation for each of the following three thematic areas: clinical specialties ( Obstetrics & Gynecology and Revista Española de Cardiología) ; Public Health and Epidemiology ( International Journal of Epidemiology and Atención Primaria) and the area of general and internal medicine ( British Medical Journal and Medicina Clínica ). Five of the selected journals formally endorsed ICMJE guidelines; the remaining one ( Revista Española de Cardiología ) suggests observing ICMJE demands in relation with specific issues. We attempted to capture journal diversity in the sample by selecting general and specialty journals with different degrees of influence, resulting from their impact factors in 2007, which oscillated between 1.337 (MC) and 9.723 (BMJ). No special reasons guided us to choose these specific journals, but we opted for journals with rather large paid circulations. For instance, the Spanish Cardiology Journal is the one with the largest impact factor among the fourteen Spanish Journals devoted to clinical specialties that have impact factor and Obstetrics & Gynecology has an outstanding impact factor among the huge number of journals available for selection.
It was decided to take around 60 papers for each biennium and journal, which means a total of around 1,000 papers. As recently suggested [ 36 , 37 ], this number was not established using a conventional method, but by means of a purposive and pragmatic approach in choosing the maximum sample size that was feasible.
Systematic sampling in phases [ 38 ] was used in applying a sampling fraction equal to 60/N, where N is the number of articles, in each of the 18 subgroups defined by crossing the six journals and the three time periods. Table 1 lists the population size and the sample size for each subgroup. While the sample within each subgroup was selected with equal probability, estimates based on other subsets of articles (defined across time periods, areas, or languages) are based on samples with various selection probabilities. Proper weights were used to take into account the stratified nature of the sampling in these cases.
Forty-nine of the 1,092 selected papers were eliminated because, although the section of the article in which they were assigned could suggest they were originals, detailed scrutiny revealed that in some cases they were not. The sample, therefore, consisted of 1,043 papers. Each of them was classified into one of three categories: (1) purely descriptive papers, those designed to review or characterize the state of affairs as it exists at present, (2) analytical papers, or (3) articles that address theoretical, methodological or conceptual issues. An article was regarded as analytical if it seeks to explain the reasons behind a particular occurrence by discovering causal relationships or, even if self-classified as descriptive, it was carried out to assess cause-effect associations among variables. We classify as theoretical or methodological those articles that do not handle empirical data as such, and focus instead on proposing or assessing research methods. We identified 169 papers as purely descriptive or theoretical, which were therefore excluded from the sample. Figure 1 presents a flow chart showing the process for determining eligibility for inclusion in the sample.
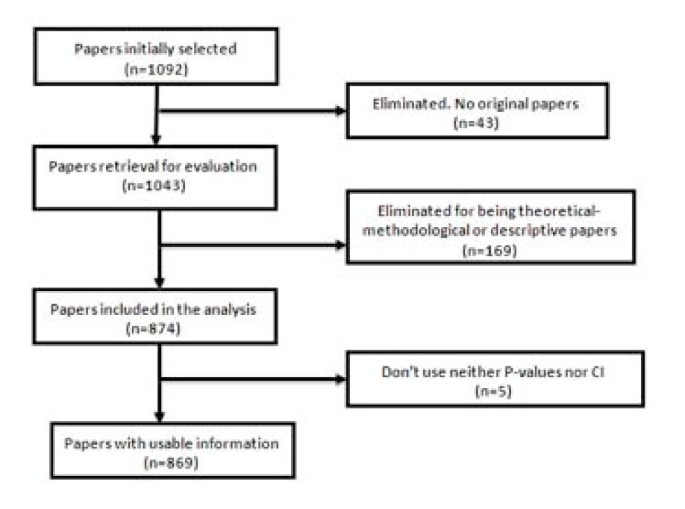
Flow chart of the selection process for eligible papers .
To estimate the adherence to ICMJE recommendations, we considered whether the papers used P-values, confidence intervals, and both simultaneously. By "the use of P-values" we mean that the article contains at least one P-value, explicitly mentioned in the text or at the bottom of a table, or that it reports that an effect was considered as statistically significant . It was deemed that an article uses CI if it explicitly contained at least one confidence interval, but not when it only provides information that could allow its computation (usually by presenting both the estimate and the standard error). Probability intervals provided in Bayesian analysis were classified as confidence intervals (although conceptually they are not the same) since what is really of interest here is whether or not the authors quantify the findings and present them with appropriate indicators of the margin of error or uncertainty.
In addition we determined whether the "Results" section of each article attributed the status of "significant" to an effect on the sole basis of the outcome of a NHST (i.e., without clarifying that it is strictly statistical significance). Similarly, we examined whether the term "significant" (applied to a test) was mistakenly used as synonymous with substantive , relevant or important . The use of the term "significant effect" when it is only appropriate as a reference to a "statistically significant difference," can be considered a direct expression of the significance fallacy [ 39 ] and, as such, constitutes one way to detect the problem in a specific paper.
We also assessed whether the "Conclusions," which sometimes appear as a separate section in the paper or otherwise in the last paragraphs of the "Discussion" section mentioned statistical significance and, if so, whether any of such mentions were no more than an allusion to results.
To perform these analyses we considered both the abstract and the body of the article. To assess the handling of the significance issue, however, only the body of the manuscript was taken into account.
The information was collected by four trained observers. Every paper was assigned to two reviewers. Disagreements were discussed and, if no agreement was reached, a third reviewer was consulted to break the tie and so moderate the effect of subjectivity in the assessment.
In order to assess the reliability of the criteria used for the evaluation of articles and to effect a convergence of criteria among the reviewers, a pilot study of 20 papers from each of three journals ( Clinical Medicine , Primary Care , and International Journal of Epidemiology) was performed. The results of this pilot study were satisfactory. Our results are reported using percentages together with their corresponding confidence intervals. For sampling errors estimations, used to obtain confidence intervals, we weighted the data using the inverse of the probability of selection of each paper, and we took into account the complex nature of the sample design. These analyses were carried out with EPIDAT [ 40 ], a specialized computer program that is readily available.
A total of 1,043 articles were reviewed, of which 874 (84%) were found to be analytic, while the remainders were purely descriptive or of a theoretical and methodological nature. Five of them did not employ either P-values or CI. Consequently, the analysis was made using the remaining 869 articles.
Use of NHST and confidence intervals
The percentage of articles that use only P-values, without even mentioning confidence intervals, to report their results has declined steadily throughout the period analyzed (Table 2 ). The percentage decreased from approximately 41% in 1995-1996 to 21% in 2005-2006. However, it does not differ notably among journals of different languages, as shown by the estimates and confidence intervals of the respective percentages. Concerning thematic areas, it is highly surprising that most of the clinical articles ignore the recommendations of ICMJE, while for general and internal medicine papers such a problem is only present in one in five papers, and in the area of Public Health and Epidemiology it occurs only in one out of six. The use of CI alone (without P-values) has increased slightly across the studied periods (from 9% to 13%), but it is five times more prevalent in Public Health and Epidemiology journals than in Clinical ones, where it reached a scanty 3%.
Ambivalent handling of the significance
While the percentage of articles referring implicitly or explicitly to significance in an ambiguous or incorrect way - that is, incurring the significance fallacy -- seems to decline steadily, the prevalence of this problem exceeds 69%, even in the most recent period. This percentage was almost the same for articles written in Spanish and in English, but it was notably higher in the Clinical journals (81%) compared to the other journals, where the problem occurs in approximately 7 out of 10 papers (Table 3 ). The kappa coefficient for measuring agreement between observers concerning the presence of the "significance fallacy" was 0.78 (CI95%: 0.62 to 0.93), which is considered acceptable in the scale of Landis and Koch [ 41 ].
Reference to numerical results or statistical significance in Conclusions
The percentage of papers mentioning a numerical finding as a conclusion is similar in the three periods analyzed (Table 4 ). Concerning languages, this percentage is nearly twice as large for Spanish journals as for those published in English (approximately 21% versus 12%). And, again, the highest percentage (16%) corresponded to clinical journals.
A similar pattern is observed, although with less pronounced differences, in references to the outcome of the NHST (significant or not) in the conclusions (Table 5 ). The percentage of articles that introduce the term in the "Conclusions" does not appreciably differ between articles written in Spanish and in English. Again, the area where this insufficiency is more often present (more than 15% of articles) is the Clinical area.
There are some previous studies addressing the degree to which researchers have moved beyond the ritualistic use of NHST to assess their hypotheses. This has been examined for areas such as biology [ 42 ], organizational research [ 43 ], or psychology [ 44 – 47 ]. However, to our knowledge, no recent research has explored the pattern of use P-values and CI in medical literature and, in any case, no efforts have been made to study this problem in a way that takes into account different languages and specialties.
At first glance it is puzzling that, after decades of questioning and technical warnings, and after twenty years since the inception of ICMJE recommendation to avoid NHST, they continue being applied ritualistically and mindlessly as the dominant doctrine. Not long ago, when researchers did not observe statistically significant effects, they were unlikely to write them up and to report "negative" findings, since they knew there was a high probability that the paper would be rejected. This has changed a bit: editors are more prone to judge all findings as potentially eloquent. This is probably the frequent denunciations of the tendency for those papers presenting a significant positive result to receive more favorable publication decisions than equally well-conducted ones that report a negative or null result, the so-called publication bias [ 48 – 50 ]. This new openness is consistent with the fact that if the substantive question addressed is really relevant, the answer (whether positive or negative) will also be relevant.
Consequently, even though it was not an aim of our study, we found many examples in which statistical significance was not obtained. However, many of those negative results were reported with a comment of this type: " The results did not show a significant difference between groups; however, with a larger sample size, this difference would have probably proved to be significant ". The problem with this statement is that it is true; more specifically, it will always be true and it is, therefore, sterile. It is not fortuitous that one never encounters the opposite, and equally tautological, statement: " A significant difference between groups has been detected; however, perhaps with a smaller sample size, this difference would have proved to be not significant" . Such a double standard is itself an unequivocal sign of the ritual application of NHST.
Although the declining rates of NHST usage show that, gradually, ICMJE and similar recommendations are having a positive impact, most of the articles in the clinical setting still considered NHST as the final arbiter of the research process. Moreover, it appears that the improvement in the situation is mostly formal, and the percentage of articles that fall into the significance fallacy is huge.
The contradiction between what has been conceptually recommended and the common practice is sensibly less acute in the area of Epidemiology and Public Health, but the same pattern was evident everywhere in the mechanical way of applying significance tests. Nevertheless, the clinical journals remain the most unmoved by the recommendations.
The ICMJE recommendations are not cosmetic statements but substantial ones, and the vigorous exhortations made by outstanding authorities [ 51 ] are not mere intellectual exercises due to ingenious and inopportune methodologists, but rather they are very serious epistemological warnings.
In some cases, the role of CI is not as clearly suitable (e.g. when estimating multiple regression coefficients or because effect sizes are not available for some research designs [ 43 , 52 ]), but when it comes to estimating, for example, an odds ratio or a rates difference, the advantage of using CI instead of P values is very clear, since in such cases it is obvious that the goal is to assess what has been called the "effect size."
The inherent resistance to change old paradigms and practices that have been entrenched for decades is always high. Old habits die hard. The estimates and trends outlined are entirely consistent with Alvan Feinstein's warning 25 years ago: "Because the history of medical research also shows a long tradition of maintaining loyalty to established doctrines long after the doctrines had been discredited, or shown to be valueless, we cannot expect a sudden change in this medical policy merely because it has been denounced by leading connoisseurs of statistics [ 53 ]".
It is possible, however, that the nature of the problem has an external explanation: it is likely that some editors prefer to "avoid troubles" with the authors and vice versa, thus resorting to the most conventional procedures. Many junior researchers believe that it is wise to avoid long back-and-forth discussions with reviewers and editors. In general, researchers who want to appear in print and survive in a publish-or-perish environment are motivated by force, fear, and expedience in their use of NHST [ 54 ]. Furthermore, it is relatively natural that simple researchers use NHST when they take into account that some theoretical objectors have used this statistical analysis in empirical studies, published after the appearance of their own critiques [ 55 ].
For example, Journal of the American Medical Association published a bibliometric study [ 56 ] discussing the impact of statisticians' co-authorship of medical papers on publication decisions by two major high-impact journals: British Medical Journal and Annals of Internal Medicine . The data analysis is characterized by methodological orthodoxy. The authors just use chi-square tests without any reference to CI, although the NHST had been repeatedly criticized over the years by two of the authors:
Douglas Altman, an early promoter of confidence intervals as an alternative [ 57 ], and Steve Goodman, a critic of NHST from a Bayesian perspective [ 58 ]. Individual authors, however, cannot be blamed for broader institutional problems and systemic forces opposed to change.
The present effort is certainly partial in at least two ways: it is limited to only six specific journals and to three biennia. It would be therefore highly desirable to improve it by studying the problem in a more detailed way (especially by reviewing more journals with different profiles), and continuing the review of prevailing patterns and trends.
Curran-Everett D: Explorations in statistics: hypothesis tests and P values. Adv Physiol Educ. 2009, 33: 81-86. 10.1152/advan.90218.2008.
Article PubMed Google Scholar
Fisher RA: Statistical Methods for Research Workers. 1925, Edinburgh: Oliver & Boyd
Google Scholar
Neyman J, Pearson E: On the use and interpretation of certain test criteria for purposes of statistical inference. Biometrika. 1928, 20: 175-240.
Silva LC: Los laberintos de la investigación biomédica. En defensa de la racionalidad para la ciencia del siglo XXI. 2009, Madrid: Díaz de Santos
Berkson J: Test of significance considered as evidence. J Am Stat Assoc. 1942, 37: 325-335. 10.2307/2279000.
Article Google Scholar
Nickerson RS: Null hypothesis significance testing: A review of an old and continuing controversy. Psychol Methods. 2000, 5: 241-301. 10.1037/1082-989X.5.2.241.
Article CAS PubMed Google Scholar
Rozeboom WW: The fallacy of the null hypothesissignificance test. Psychol Bull. 1960, 57: 418-428. 10.1037/h0042040.
Callahan JL, Reio TG: Making subjective judgments in quantitative studies: The importance of using effect sizes and confidenceintervals. HRD Quarterly. 2006, 17: 159-173.
Nakagawa S, Cuthill IC: Effect size, confidence interval and statistical significance: a practical guide for biologists. Biol Rev. 2007, 82: 591-605. 10.1111/j.1469-185X.2007.00027.x.
Breaugh JA: Effect size estimation: factors to consider and mistakes to avoid. J Manage. 2003, 29: 79-97. 10.1177/014920630302900106.
Thompson B: What future quantitative social science research could look like: confidence intervals for effect sizes. Educ Res. 2002, 31: 25-32.
Matthews RA: Significance levels for the assessment of anomalous phenomena. Journal of Scientific Exploration. 1999, 13: 1-7.
Savage IR: Nonparametric statistics. J Am Stat Assoc. 1957, 52: 332-333.
Silva LC, Benavides A, Almenara J: El péndulo bayesiano: Crónica de una polémica estadística. Llull. 2002, 25: 109-128.
Goodman SN, Royall R: Evidence and scientific research. Am J Public Health. 1988, 78: 1568-1574. 10.2105/AJPH.78.12.1568.
Article CAS PubMed PubMed Central Google Scholar
Berger JO, Berry DA: Statistical analysis and the illusion of objectivity. Am Sci. 1988, 76: 159-165.
Hurlbert SH, Lombardi CM: Final collapse of the Neyman-Pearson decision theoretic framework and rise of the neoFisherian. Ann Zool Fenn. 2009, 46: 311-349.
Fidler F, Thomason N, Cumming G, Finch S, Leeman J: Editors can lead researchers to confidence intervals but they can't make them think: Statistical reform lessons from Medicine. Psychol Sci. 2004, 15: 119-126. 10.1111/j.0963-7214.2004.01502008.x.
Balluerka N, Vergara AI, Arnau J: Calculating the main alternatives to null-hypothesis-significance testing in between-subject experimental designs. Psicothema. 2009, 21: 141-151.
Cumming G, Fidler F: Confidence intervals: Better answers to better questions. J Psychol. 2009, 217: 15-26.
Jones LV, Tukey JW: A sensible formulation of the significance test. Psychol Methods. 2000, 5: 411-414. 10.1037/1082-989X.5.4.411.
Dixon P: The p-value fallacy and how to avoid it. Can J Exp Psychol. 2003, 57: 189-202.
Nakagawa S, Cuthill IC: Effect size, confidence interval and statistical significance: a practical guide for biologists. Biol Rev Camb Philos Soc. 2007, 82: 591-605. 10.1111/j.1469-185X.2007.00027.x.
Brandstaetter E: Confidence intervals as an alternative to significance testing. MPR-Online. 2001, 4: 33-46.
Masson ME, Loftus GR: Using confidence intervals for graphically based data interpretation. Can J Exp Psychol. 2003, 57: 203-220.
International Committee of Medical Journal Editors: Uniform requirements for manuscripts submitted to biomedical journals. Update October 2008. Accessed July 11, 2009, [ http://www.icmje.org ]
Feinstein AR: P-Values and Confidence Intervals: two sides of the same unsatisfactory coin. J Clin Epidemiol. 1998, 51: 355-360. 10.1016/S0895-4356(97)00295-3.
Haller H, Kraus S: Misinterpretations of significance: A problem students share with their teachers?. MRP-Online. 2002, 7: 1-20.
Gigerenzer G, Krauss S, Vitouch O: The null ritual: What you always wanted to know about significance testing but were afraid to ask. The Handbook of Methodology for the Social Sciences. Edited by: Kaplan D. 2004, Thousand Oaks, CA: Sage Publications, Chapter 21: 391-408.
Curran-Everett D, Taylor S, Kafadar K: Fundamental concepts in statistics: elucidation and illustration. J Appl Physiol. 1998, 85: 775-786.
CAS PubMed Google Scholar
Royall RM: Statistical evidence: a likelihood paradigm. 1997, Boca Raton: Chapman & Hall/CRC
Goodman SN: Of P values and Bayes: A modest proposal. Epidemiology. 2001, 12: 295-297. 10.1097/00001648-200105000-00006.
Sarria M, Silva LC: Tests of statistical significance in three biomedical journals: a critical review. Rev Panam Salud Publica. 2004, 15: 300-306.
Silva LC: Una ceremonia estadística para identificar factores de riesgo. Salud Colectiva. 2005, 1: 322-329.
Goodman SN: Toward Evidence-Based Medical Statistics 1: The p Value Fallacy. Ann Intern Med. 1999, 130: 995-1004.
Schulz KF, Grimes DA: Sample size calculations in randomised clinical trials: mandatory and mystical. Lancet. 2005, 365: 1348-1353. 10.1016/S0140-6736(05)61034-3.
Bacchetti P: Current sample size conventions: Flaws, harms, and alternatives. BMC Med. 2010, 8: 17-10.1186/1741-7015-8-17.
Article PubMed PubMed Central Google Scholar
Silva LC: Diseño razonado de muestras para la investigación sanitaria. 2000, Madrid: Díaz de Santos
Barnett ML, Mathisen A: Tyranny of the p-value: The conflict between statistical significance and common sense. J Dent Res. 1997, 76: 534-536. 10.1177/00220345970760010201.
Santiago MI, Hervada X, Naveira G, Silva LC, Fariñas H, Vázquez E, Bacallao J, Mújica OJ: [The Epidat program: uses and perspectives] [letter]. Pan Am J Public Health. 2010, 27: 80-82. Spanish.
Landis JR, Koch GG: The measurement of observer agreement for categorical data. Biometrics. 1977, 33: 159-74. 10.2307/2529310.
Fidler F, Burgman MA, Cumming G, Buttrose R, Thomason N: Impact of criticism of null-hypothesis significance testing on statistical reporting practices in conservation biology. Conserv Biol. 2005, 20: 1539-1544. 10.1111/j.1523-1739.2006.00525.x.
Kline RB: Beyond significance testing: Reforming data analysis methods in behavioral research. 2004, Washington, DC: American Psychological Association
Book Google Scholar
Curran-Everett D, Benos DJ: Guidelines for reporting statistics in journals published by the American Physiological Society: the sequel. Adv Physiol Educ. 2007, 31: 295-298. 10.1152/advan.00022.2007.
Hubbard R, Parsa AR, Luthy MR: The spread of statistical significance testing: The case of the Journal of Applied Psychology. Theor Psychol. 1997, 7: 545-554. 10.1177/0959354397074006.
Vacha-Haase T, Nilsson JE, Reetz DR, Lance TS, Thompson B: Reporting practices and APA editorial policies regarding statistical significance and effect size. Theor Psychol. 2000, 10: 413-425. 10.1177/0959354300103006.
Krueger J: Null hypothesis significance testing: On the survival of a flawed method. Am Psychol. 2001, 56: 16-26. 10.1037/0003-066X.56.1.16.
Rising K, Bacchetti P, Bero L: Reporting Bias in Drug Trials Submitted to the Food and Drug Administration: Review of Publication and Presentation. PLoS Med. 2008, 5: e217-10.1371/journal.pmed.0050217. doi:10.1371/journal.pmed.0050217
Sridharan L, Greenland L: Editorial policies and publication bias the importance of negative studies. Arch Intern Med. 2009, 169: 1022-1023. 10.1001/archinternmed.2009.100.
Falagas ME, Alexiou VG: The top-ten in journal impact factor manipulation. Arch Immunol Ther Exp (Warsz). 2008, 56: 223-226. 10.1007/s00005-008-0024-5.
Rothman K: Writing for Epidemiology. Epidemiology. 1998, 9: 98-104. 10.1097/00001648-199805000-00019.
Fidler F: The fifth edition of the APA publication manual: Why its statistics recommendations are so controversial. Educ Psychol Meas. 2002, 62: 749-770. 10.1177/001316402236876.
Feinstein AR: Clinical epidemiology: The architecture of clinical research. 1985, Philadelphia: W.B. Saunders Company
Orlitzky M: Institutionalized dualism: statistical significance testing as myth and ceremony. Accessed Feb 8, 2010, [ http://ssrn.com/abstract=1415926 ]
Greenwald AG, González R, Harris RJ, Guthrie D: Effect sizes and p-value. What should be reported and what should be replicated?. Psychophysiology. 1996, 33: 175-183. 10.1111/j.1469-8986.1996.tb02121.x.
Altman DG, Goodman SN, Schroter S: How statistical expertise is used in medical research. J Am Med Assoc. 2002, 287: 2817-2820. 10.1001/jama.287.21.2817.
Gardner MJ, Altman DJ: Statistics with confidence. Confidence intervals and statistical guidelines. 1992, London: BMJ
Goodman SN: P Values, Hypothesis Tests and Likelihood: implications for epidemiology of a neglected historical debate. Am J Epidemiol. 1993, 137: 485-496.
Pre-publication history
The pre-publication history for this paper can be accessed here: http://www.biomedcentral.com/1471-2288/10/44/prepub
Download references
Acknowledgements
The authors would like to thank Tania Iglesias-Cabo and Vanesa Alvarez-González for their help with the collection of empirical data and their participation in an earlier version of the paper. The manuscript has benefited greatly from thoughtful, constructive feedback by Carlos Campillo-Artero, Tom Piazza and Ann Séror.
Author information
Authors and affiliations.
Centro Nacional de Investigación de Ciencias Médicas, La Habana, Cuba
Luis Carlos Silva-Ayçaguer
Unidad de Investigación. Hospital de Cabueñes, Servicio de Salud del Principado de Asturias (SESPA), Gijón, Spain
Patricio Suárez-Gil
CIBER Epidemiología y Salud Pública (CIBERESP), Spain and Departamento de Medicina, Unidad de Epidemiología Molecular del Instituto Universitario de Oncología, Universidad de Oviedo, Spain
Ana Fernández-Somoano
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Patricio Suárez-Gil .
Additional information
Competing interests.
The authors declare that they have no competing interests.
Authors' contributions
LCSA designed the study, wrote the paper and supervised the whole process; PSG coordinated the data extraction and carried out statistical analysis, as well as participated in the editing process; AFS extracted the data and participated in the first stage of statistical analysis; all authors contributed to and revised the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Authors’ original file for figure 1
Rights and permissions.
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Reprints and permissions
About this article
Cite this article.
Silva-Ayçaguer, L.C., Suárez-Gil, P. & Fernández-Somoano, A. The null hypothesis significance test in health sciences research (1995-2006): statistical analysis and interpretation. BMC Med Res Methodol 10 , 44 (2010). https://doi.org/10.1186/1471-2288-10-44
Download citation
Received : 29 December 2009
Accepted : 19 May 2010
Published : 19 May 2010
DOI : https://doi.org/10.1186/1471-2288-10-44
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Clinical Specialty
- Significance Fallacy
- Null Hypothesis Statistical Testing
- Medical Journal Editor
- Clinical Journal
BMC Medical Research Methodology
ISSN: 1471-2288
- General enquiries: [email protected]
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null & Alternative Hypotheses | Definitions, Templates & Examples
Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis ( H 0 ): There’s no effect in the population .
- Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:
- The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
- The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question.
- They both make claims about the population.
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
General template sentences
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
- Alternative hypothesis ( H a ): Independent variable affects dependent variable.
Test-specific template sentences
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved October 16, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/
Is this article helpful?

Shaun Turney
Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.
- Science, Tech, Math ›
- Chemistry ›
- Scientific Method ›
Null Hypothesis Examples
ThoughtCo / Hilary Allison
- Scientific Method
- Chemical Laws
- Periodic Table
- Projects & Experiments
- Biochemistry
- Physical Chemistry
- Medical Chemistry
- Chemistry In Everyday Life
- Famous Chemists
- Activities for Kids
- Abbreviations & Acronyms
- Weather & Climate
- Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
- B.A., Physics and Mathematics, Hastings College
In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.
The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.
What Is the Null Hypothesis?
The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.
To distinguish it from other hypotheses , the null hypothesis is written as H 0 (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.
Examples of the Null Hypothesis
To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.
| Are teens better at math than adults? | Age has no effect on mathematical ability. |
| Does taking aspirin every day reduce the chance of having a heart attack? | Taking aspirin daily does not affect heart attack risk. |
| Do teens use cell phones to access the internet more than adults? | Age has no effect on how cell phones are used for internet access. |
| Do cats care about the color of their food? | Cats express no food preference based on color. |
| Does chewing willow bark relieve pain? | There is no difference in pain relief after chewing willow bark versus taking a placebo. |
Other Types of Hypotheses
In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."
Key Takeaways
- In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
- Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
- By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
- What Are Examples of a Hypothesis?
- Random Error vs. Systematic Error
- Six Steps of the Scientific Method
- What Is a Hypothesis? (Science)
- Scientific Method Flow Chart
- What Are the Elements of a Good Hypothesis?
- Scientific Method Vocabulary Terms
- Understanding Simple vs Controlled Experiments
- The Role of a Controlled Variable in an Experiment
- What Is an Experimental Constant?
- What Is a Testable Hypothesis?
- Scientific Hypothesis Examples
- What Is the Difference Between a Control Variable and Control Group?
- DRY MIX Experiment Variables Acronym
- What Is a Controlled Experiment?
- Scientific Variable
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
10.1 - setting the hypotheses: examples.
A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.
Example 10.2: Hypotheses with One Sample of One Categorical Variable Section
About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.
- Research Question : Are artists more likely to be left-handed than people found in the general population?
- Response Variable : Classification of the student as either right-handed or left-handed
State Null and Alternative Hypotheses
- Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
- Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.
Example 10.3: Hypotheses with One Sample of One Measurement Variable Section

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.
- Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
- Response Variable : dosage of the active ingredient found by a chemical assay.
- Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
- Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.
Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.
- Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
- Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
- Explanatory (Grouping) Variable: Sex
- Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
- Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.
Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.
- Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
- Response Variable : Weight loss (pounds)
- Explanatory (Grouping) Variable : Type of diet
- Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
- Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.
Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section
- Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
- Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
- Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
- Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.
This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.
Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section
- Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
- Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
- Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
- Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.
Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section
- Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
- Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
- Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
- Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Hypothesis Testing with One Sample
Null and Alternative Hypotheses
OpenStaxCollege
[latexpage]
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
H 0 : The drug reduces cholesterol by 25%. p = 0.25
H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
H 0 : μ = 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ = 66
- H a : μ ≠ 66
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
H 0 : μ ≥ 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ ≥ 45
- H a : μ < 45
In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
H 0 : p ≤ 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p = 0.40
- H a : p > 0.40
<!– ??? –>
Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
Chapter Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:
Formula Review
H 0 and H a are contradictory.
| has: | equal (=) | greater than or equal to (≥) | less than or equal to (≤) |
| has: | not equal (≠) greater than (>) less than (<) | less than (<) | greater than (>) |
If α ≤ p -value, then do not reject H 0 .
If α > p -value, then reject H 0 .
α is preconceived. Its value is set before the hypothesis test starts. The p -value is calculated from the data.
You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. What is the random variable? Describe in words.
The random variable is the mean Internet speed in Megabits per second.
You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. State the null and alternative hypotheses.
The American family has an average of two children. What is the random variable? Describe in words.
The random variable is the mean number of children an American family has.
The mean entry level salary of an employee at a company is 💲58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.
A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.
The random variable is the proportion of people picked at random in Times Square visiting the city.
A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.
In a population of fish, approximately 42% are female. A test is conducted to see if, in fact, the proportion is less. State the null and alternative hypotheses.
Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.
A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?
- H 0 : __________
- H a : __________
- H 0 : μ = 15
- H a : μ ≠ 15
The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?
Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.
State the null hypothesis, H 0 , and the alternative hypothesis. H a , in terms of the appropriate parameter ( μ or p ).
- The mean number of years Americans work before retiring is 34.
- At most 60% of Americans vote in presidential elections.
- The mean starting salary for San Jose State University graduates is at least 💲100,000 per year.
- Twenty-nine percent of high school seniors get drunk each month.
- Fewer than 5% of adults ride the bus to work in Los Angeles.
- The mean number of cars a person owns in her lifetime is not more than ten.
- About half of Americans prefer to live away from cities, given the choice.
- Europeans have a mean paid vacation each year of six weeks.
- The chance of developing breast cancer is under 11% for women.
- Private universities’ mean tuition cost is more than 💲20,000 per year.
- H 0 : μ = 34; H a : μ ≠ 34
- H 0 : p ≤ 0.60; H a : p > 0.60
- H 0 : μ ≥ 100,000; H a : μ < 100,000
- H 0 : p = 0.29; H a : p ≠ 0.29
- H 0 : p = 0.05; H a : p < 0.05
- H 0 : μ ≤ 10; H a : μ > 10
- H 0 : p = 0.50; H a : p ≠ 0.50
- H 0 : μ = 6; H a : μ ≠ 6
- H 0 : p ≥ 0.11; H a : p < 0.11
- H 0 : μ ≤ 20,000; H a : μ > 20,000
Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:
- p < 0.30
- p > 0.30
A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:
- p > 0.20
- p < 0.20
Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:
- H o : \(\overline{x}\) = 4.5, H a : \(\overline{x}\) > 4.5
- H o : μ ≥ 4.5, H a : μ < 4.5
- H o : μ = 4.75, H a : μ > 4.75
- H o : μ = 4.5, H a : μ > 4.5
Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.
Null and Alternative Hypotheses Copyright © 2013 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Have a thesis expert improve your writing
Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null and Alternative Hypotheses | Definitions & Examples
Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis (H 0 ): There’s no effect in the population .
- Alternative hypothesis (H A ): There’s an effect in the population.
The effect is usually the effect of the independent variable on the dependent variable .
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question
- They both make claims about the population
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
- Alternative hypothesis (H A ): Independent variable affects dependent variable .
Test-specific
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 15 October 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/
Is this article helpful?

Shaun Turney
Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.
An official website of the United States government
Official websites use .gov A .gov website belongs to an official government organization in the United States.
Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.
- Publications
- Account settings
- Advanced Search
- Journal List

Why we habitually engage in null-hypothesis significance testing: A qualitative study
Jonah stunt, leonie van grootel, david trafimow, trynke hoekstra, michiel de boer.
- Author information
- Article notes
- Copyright and License information
Competing Interests: David Trafimow is editor of Basic and Applied Social Psychology BASP, the journal that prohibited the use of NHST, p-values and confidence intervals. The authors JS, LvG, LB, DT and MdB of this article have the conviction that the use of NHST should be discouraged and replaced by better methods.
* E-mail: [email protected]
Received 2020 Nov 20; Accepted 2021 Sep 24; Collection date 2021.
This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Null Hypothesis Significance Testing (NHST) is the most familiar statistical procedure for making inferences about population effects. Important problems associated with this method have been addressed and various alternatives that overcome these problems have been developed. Despite its many well-documented drawbacks, NHST remains the prevailing method for drawing conclusions from data. Reasons for this have been insufficiently investigated. Therefore, the aim of our study was to explore the perceived barriers and facilitators related to the use of NHST and alternative statistical procedures among relevant stakeholders in the scientific system.
Individual semi-structured interviews and focus groups were conducted with junior and senior researchers, lecturers in statistics, editors of scientific journals and program leaders of funding agencies. During the focus groups, important themes that emerged from the interviews were discussed. Data analysis was performed using the constant comparison method, allowing emerging (sub)themes to be fully explored. A theory substantiating the prevailing use of NHST was developed based on the main themes and subthemes we identified.
Twenty-nine interviews and six focus groups were conducted. Several interrelated facilitators and barriers associated with the use of NHST and alternative statistical procedures were identified. These factors were subsumed under three main themes: the scientific climate, scientific duty, and reactivity. As a result of the factors, most participants feel dependent in their actions upon others, have become reactive, and await action and initiatives from others. This may explain why NHST is still the standard and ubiquitously used by almost everyone involved.
Our findings demonstrate how perceived barriers to shift away from NHST set a high threshold for actual behavioral change and create a circle of interdependency between stakeholders. By taking small steps it should be possible to decrease the scientific community’s strong dependence on NHST and p-values.
Introduction
Empirical studies often start from the idea that there might be an association between a specific factor and a certain outcome within a population. This idea is referred to as the alternative hypothesis (H1). Its complement, the null hypothesis (H0), typically assumes no association or effect (although it is possible to test other effect sizes than no effect with the null hypothesis). At the stage of data-analysis, the probability of obtaining the observed, or a more extreme, association is calculated under the assumption of no effect in the population (H0) and a number of inferential assumptions [ 1 ]. The probability of obtaining the observed, or more extreme, data is known as ‘the p-value’. The p-value demonstrates the compatibility between the observed data and the expected data under the null hypothesis, where 0 is complete incompatibility and 1 is perfect compatibility [ 2 ]. When the p-value is smaller than a prespecified value (labelled as alpha, usually set at 5% (0.05)), results are generally declared to be statistically significant. At this point, researchers commonly reject the null hypothesis and accept the alternative hypothesis [ 2 ]. Assessing statistical significance by means of contrasting the data with the null hypothesis is called Null Hypothesis Significance Testing (NHST). NHST is the best known and most widely used statistical procedure for making inferences about population effects. The procedure has become the prevailing paradigm in empirical science [ 3 ], and reaching and being able to report statistically significant results has become the ultimate goal for many researchers.
Despite its widespread use, NHST and the p-value have been criticized since its inception. Numerous publications have addressed problems associated with NHST and p-values. Arguably the most important drawback is the fact that NHST is a form of indirect or inverse inference: researchers usually want to know if the null or alternative hypothesis can be accepted and use NHST to conclude either way. But with NHST, the probability of a finding, or more extreme findings, given the null hypothesis is calculated [ 4 ]. Ergo, NHST doesn’t tell us what we want to know. In fact, p-values were never meant to serve as a basis to draw conclusions, but as a continuous measure of incompatibility between empirical findings and a statistical model [ 2 ]. Moreover, the procedure promotes a dichotomous way of thinking, by using the outcome of a significance test as a dichotomous indicator for an effect (p<0.05: effect, p>0.05: no effect). Reducing empirical findings to two categories also results in a great loss of information. Further, a significant outcome is often unjustly interpreted as relevant, but a p-value does not convey any information about the strength or importance of the association. Worse yet, the p-values on which NHST is based confound effect size and sample size. A trivial effect size may nevertheless result in statistical significance provided a sufficiently large sample size. Or an important effect size may fail to result in statistical significance if the sample size is too small. P-values do not validly index the size, relevance, or precision of an effect [ 5 ]. Furthermore, statistical models include not only null hypotheses, but additional assumptions, some of which are wrong, such as the ubiquitous assumption of random and independent sampling from a defined population [ 1 ]. Therefore, although p-values validly index the incompatibility of data with models, p-values do not validly index incompatibility of data with hypotheses that are embedded in wrong models. These are important drawbacks rendering NHST unsuitable as the default procedure for drawing conclusions from empirical data [ 2 , 3 , 5 – 13 ].
A number of alternatives have been developed that overcome these pitfalls, such as Bayesian inference methods [ 7 , 11 , 14 , 15 ], informative hypothesis testing [ 9 , 16 ] and a priori inferential statistics [ 4 , 17 ]. These alternatives build on the idea that research usually starts with a more informed research-question than one merely assuming the null hypothesis of no effect. These methods overcome the problem of inverse inference, although the first two might still lead to dichotomous thinking with the use of thresholds. Despite the availability of alternatives, statistical behavior in the research community has hardly changed. Researchers have been slow to adopt alternative methods and NHST is still the prevailing paradigm for making inferences about population effects [ 3 ].
Until now, reasons for the continuous and ubiquitous use of NHST and the p-value have scarcely been investigated. One explanation is that NHST provides a very simple means for drawing conclusions from empirical data, usually based on the 5% cut-off. Secondly, most researchers are unaware of the pitfalls of NHST; it has been shown that NHST and the p-value are often misunderstood and misinterpreted [ 2 , 3 , 8 , 11 , 18 , 19 ]. Thirdly, NHST has a central role in most methods and statistics courses in higher education. Courses on alternative methods are increasingly being offered but are usually not mandatory. To our knowledge, there is a lack of in depth, empirical research, aimed at elucidating why NHST nevertheless remains the dominant approach, or what actions can be taken to shift the sciences away from NHST. Therefore, the aim of our study was to explore the perceived barriers and facilitators, as well as behavioral intentions related to the use of NHST and alternatives statistical procedures, among all relevant stakeholders in the scientific system.
Theoretical framework
In designing our study, we used two theories. Firstly, we used the ‘diffusion of innovation theory’ of Rogers [ 20 ]. This theory describes the dissemination of an innovation as a process consisting of four elements: 1) an innovation is 2) communicated through certain channels 3) over time 4) among the members of a social system [ 20 ]. In the current study, the innovation consists of the idea that we should stop with the default use of NHST and instead consider using alternative methods for drawing conclusions from empirical data. The science system forms the social structure in which the innovation should take place. The most important members, and potential adopters of the innovation, we identified are researchers, lecturers, editors of scientific journals and representatives of funding agencies. Rogers describes phases in the adoption process, which coincide with characteristics of the (potential) adopters of the idea: 1) innovators, 2) early adopters, 3) early majority adopters, 4) late majority adopters and 5) laggards. Innovators are the first to adopt an innovation. There are few innovators but these few are very important for bringing in new ideas. Early adopters form the second group to adopt an innovation. This group includes opinion leaders and role models for other stakeholders. The largest group consists of the early and late majority who follow the early adopters, and then there is a smaller group of laggards who resist the innovation until they are certain the innovation will not fail. The process of innovation adoption by individuals is described as a normal distribution ( Fig 1 ). For these five groups, the adoption of a new idea is influenced by the following five characteristics of the innovative idea and 1) its relative advantage, 2) its compatibility with current experiences, 3) its complexity, 4) its flexibility, and 5) its visibility [ 20 ]. Members of all four stakeholder groups could play an important role in the diffusion of the innovation of replacing NHST by its alternatives.
Fig 1. Adopter categorization.
The innovativeness dimension, measured by the time at which an individual from an adopter category adopts an innovation. Each category is one of more standard deviations removed from the average time of adoption [ 20 ].
Another important theory for our study is the ‘theory of planned behavior’, that was developed in the 1960s [ 21 ]. This theory describes how human behavior in a certain context can be predicted and explained. The theory was updated in 2010, under the name ‘the reasoned action approach’ [ 22 ]. A central factor in this theory is the intention to perform a certain behavior, in this case, to change the default use of NHST. According to the theory, people’s intentions determine their behaviors. An intention indexes to what extent someone is motivated to perform the behavior. Intentions are determined by three independent determinants: the person’s attitudes toward the behavior—the degree to which a person sees the behavior as favorable or unfavorable, perceived subjective norms regarding the behavior—the perceived social pressure to perform the behavior or not, and perceptions of control regarding the behavior—the perceived ease or difficulty of performing the behavior. Underlying (i.e. responsible for) these three constructs are corresponding behavioral, normative, and control beliefs [ 21 , 22 ] (see Fig 2 ).
Fig 2. Theory of planned behavior [ 21 ].
Both theories have served as a lens for both data collection and analysis. We used sensitizing concepts [ 23 ] within the framework of the grounded theory approach [ 24 ] from both theories as a starting point for this qualitative study, and more specifically, for the topic list for the interviews and focus groups, providing direction and guidance for the data collection and data analysis.
Many of the concepts of Rogers’ and Fishbein and Ajzen’s theory can be seen as facilitators and barriers for embracing and implementing innovation in the scientific system.
A qualitative study among stakeholders using semi-structured interviews and focus groups was performed. Data collection and analysis were guided by the principle of constant comparison traditional to the grounded theory approach we followed [ 24 ]. The grounded theory is a methodology that uses inductive reasoning, and aims to construct a theory through the collection and analysis of data. Constant comparison is the iterative process whereby each part of the data that emerges from the data analysis is compared with other parts of the data to thoroughly explore and validate the data. Concepts that have been extracted from the data are tagged with codes that are grouped into categories. These categories constitute themes, which (may) become the basis for a new theory. Data collection and analysis were continued until no new information was gained and data saturation had likely occurred within the identified themes.
The target population consisted of stakeholders relevant to our topic: junior and senior researchers, lecturers in statistics, editors of scientific journals and program leaders of funding agencies (see Tables 1 and 2 ). We approached participants in the field of medical sciences, health- and life sciences and psychology. In line with the grounded theory approach, theoretical sampling was used to identify and recruit eligible participants. Theoretical sampling is a form of purposive sampling. This means that we aimed to purposefully select participants, based on their characteristics that fit the parameters of the research questions [ 25 ]. Recruitment took place by approaching persons in our professional networks and or the networks of the approached persons.
Table 1. General overview of participants.
| Stakeholder group: | ||
|---|---|---|
| : | ||
| 13 | 6:7 | |
| 15 | 8:7 | |
| 11 | 5:6 | |
| 8 | 3:5 |
Table 2. Characteristics of the participants split up by interviews and focus groups.
| Stakeholder group: | Workplace: | ||||
|---|---|---|---|---|---|
| 2 | 1 | 1 | 4 | ||
| 9 | 9 | ||||
| 4 | 4 | 8 | |||
| 8 | 8 | ||||
| 5 | 1 | 3 (1) | 9 | ||
| 9 (3 ) | 4 (2) | 13 | |||
| 2 (1) | 1 | 3 | |||
| 2 (2) | 2 | ||||
*The numbers between brackets represents the number of participants that were also interviewed.
Data collection
We conducted individual semi-structured interviews followed by focus groups. The aim of the interviews was to gain insight into the views of participants on the use of NHST and alternative methods and to examine potential barriers and facilitators related to these methods. The aim of the focus groups was to validate and further explore interview findings and to develop a comprehensive understanding of participants’ views and beliefs.
For the semi-structured interviews, we used a topic list (see Appendix 1 in S1 Appendix ). Questions addressed participants’ knowledge and beliefs about the concept of NHST, their familiarity with NHST, perceived attractiveness and drawbacks of the use of NHST, knowledge of the current NHST debate, knowledge of and views on alternative procedures and their views on the future of NHST. The topic list was slightly adjusted based on the interviews with editors and representatives from funding agencies (compared to the topic list for interviews with researchers and lecturers). Questions particularly focused on research and education were replaced by questions focused on policy (see Appendix 1 in S1 Appendix ).
The interviews were conducted between October 2017 and June 2018 by two researchers (L.v.G. and J.S.), both trained in qualitative research methods. Interviews lasted about one hour (range 31–86 minutes) and were voice-recorded. One interview was conducted by telephone; all others were face to face and took place at a location convenient for the participants, in most cases the participants’ work location.
Focus groups
During the focus groups, important themes that emerged from the interviews were discussed and explored. These include perceptions on NHST and alternatives and essential conditions to shift away from the default use of NHST.
Five focus groups included representatives from the different stakeholder groups. One focus group was homogenous, including solely lecturers. The focus groups consisted of ‘old’ as well as ‘new’ participants, that is, some of the participants of the focus groups were also in the interview sample. We also selected persons that were open for further contribution to the NHST debate and were willing to help think about (implementing) alternatives for NHST.
The focus groups were conducted between September and December 2018 by three researchers (L.v.G., J.S. and A.d.K.), all trained in qualitative research methods. The focus groups lasted about one-and-a-half hours (range 86–100 minutes).
Data analysis
All interviews and focus groups were transcribed verbatim. Atlas.ti 8.0 software was used for data management and analysis. All transcripts were read thoroughly several times to identify meaningful and relevant text fragments and analyzed by two researchers (J.S. and L.v.G.). Deductive predefined themes and theoretical concepts were used to guide the development of the topic list for the semi-structured interviews and focus groups, and were used as sensitizing concepts [ 23 ] in data collection and data analysis. Inductive themes were identified during the interview process and analysis of the data [ 26 ].
Transcripts were open-, axial- and selectively coded by two researchers (J.S. and L.v.G.). Open coding is the first step in the data-analysis, whereby phenomena found in the text are identified and named (coded). With axial coding, connections between codes are drawn. Selective coding is the process of selecting one central category and relating all other categories to that category, capturing the essence of the research. The constant comparison method [ 27 ] was applied allowing emerging (sub)themes to be fully explored. First, the two researchers independently developed a set of initial codes. Subsequently, findings were discussed until consensus was reached. Codes were then grouped into categories that were covered under subthemes, belonging to main themes. Finally, a theory substantiating the prevailing use of NHST was developed based on the main themes and subthemes.
Ethical issues
This research was conducted in accordance with the Dutch "General Data Protection Regulation" and the “Netherland’s code of conduct for research integrity”. The research protocol had been submitted for review and approved by the ethical review committee of the VU Faculty of Behavioral and Movement Sciences. In addition, the project had been submitted to the Medical Ethics Committee (METC) of the Amsterdam University Medical Centre who decided that the project is not subject to the Medical Research (Human Subjects) Act ( WMO). At the start of data collection, all participants signed an informed consent form.
A full study protocol, including a detailed data analysis plan, was preregistered ( https://osf.io/4qg38/ ). At the start of this study, preregistration forms for qualitative studies were not developed yet. Therefore, preregistration for this study is based on an outdated form. Presently, there is a preregistration form available for qualitative studies [ 28 ]. Information about data collection, data management, data sharing and data storage is described in a Data Management Plan. Sensitive data is stored in Darkstor, an offline archive for storing sensitive information or data (information that involves i.e., privacy or copyright). As the recordings and transcripts of the interviews and focus groups contain privacy-sensitive data, these files are archived in Darkstor and can be accessed only on request by authorized individuals (i.e., the original researcher or a research coordinator) (Data requests can be send to [email protected] ). Non-sensitive data is stored in DANS ( https://doi.org/10.17026/dans-2at-nzfs ) (Data Archiving and Networked Services; the Netherlands institute for permanent access to digital research resources).
Participant characteristics
Twenty-nine individual interviews and six focus groups were conducted. The focus groups included four to six participants per session. A total of 47 participants were included in the study (13 researchers, 15 lecturers, 11 editors of scientific journals and 8 representatives of funding agencies). Twenty-nine participants were interviewed. Twenty-seven participants took part in the focus group. Nine of the twenty-seven participants were both interviewed and took part in the focus groups. Some participants had multiple roles (i.e., editor and researcher, editor and lecturer or lecturer and researcher) but were classified based on their primary role (assistant professors were classified as lecturers). The lecturers in statistics in our sample were not statisticians themselves. Although they all received training in statistics, they were primarily trained as psychologists, medical doctors, or health scientists. Some lecturers in our sample taught an applied subject, with statistics as part of it. Other lectures taught Methodology and Statistics courses. Statistical skills and knowledge among lecturers varied from modest to quite advanced. Statistical skills and knowledge among participants from the other stakeholder groups varied from poor to quite advanced. All participants were working in the Netherlands. A general overview of the participants is presented in Table 1 . Participant characteristics split up by interviews and focus groups are presented in Table 2 .
Three main themes with sub-themes and categories emerged ( Fig 3 ): the green-colored compartments hold the three main themes: The scientific climate , The scientific duty and Reactivity . Each of these three main themes consists of subthemes, depicted by the yellow-colored compartments. In turn, some (but not all) of the 9 subthemes also have categories. These ‘lower level’ findings are not included in the figure but will be mentioned in the elaboration on the findings and are depicted in Appendix 2 in S1 Appendix . Fig 3 shows how the themes are related to each other. The blue arrows indicate that the themes are interrelated; factors influence each other. The scientific climate affects the way stakeholders perceive and fulfil their scientific duty, the way stakeholders give substance to their scientific duty shapes and maintain the scientific climate. The scientific duty and the scientific climate cause a state of reactivity. Many participants have adopted a ’wait and see’ attitude regarding behavioral changes with respect to statistical methods. They feel dependent on someone else’s action. This leads to a reactive (instead of a proactive) attitude and a low sense of responsibility. ‘Reactivity’ is the core theme, explaining the most critical problem with respect to the continuous and ubiquitous use of NHST.
Fig 3. The coding scheme, representing the main and subthemes and how they are interrelated.
Main themes and subthemes are numbered. Categories are mentioned in the body of the text in bold. ‘P’ stands for participant; ‘I’ stands for interviewer.
1. The scientific climate
The theme, ‘the scientific climate’, represents researchers’ (Dutch) perceptions of the many written and unwritten rules they face in the research environment. This theme concerns the opportunities and challenges participants encounter when working in the science system. Dutch academics feel pressured to publish fast and regularly, and to follow conventions and directions of those on whom they depend. They feel this comes at the expense of the quality of their work. Thus, the scientific climate in the Netherlands has a strong influence on the behavior of participants regarding how they set their priorities and control the quality of their work.
1 . 1 Quality control . Monitoring the quality of research is considered very important. Researchers, funding agencies and editors indicate they rely on their own knowledge, expertise, and insight, and those of their colleagues, to guarantee this quality. However, editors or funding agencies are often left with little choice when it comes to compiling an evaluation committee or a review panel. The choice is often like-knows-like-based. Given the limited choice, they are forced to trust the opinion of their consultants, but the question is whether this is justified.
I: “The ones who evaluate the statistics, do they have sufficient statistical knowledge?” P: “Ehhr, no, I don’t think so.” I: “Okay, interesting. So, there are manuscripts published of which you afterwards might think….” P: “Yes yes.” (Interview 18; Professor/editor, Medical Sciences)
1 . 2 Convention . The scientific system is built on mores and conventions, as this participant describes:
P: “There is science, and there is the sociology of science, that is, how we talk to each other, what we believe, how we connect. And at some point, it was agreed upon that we would talk to each other in this way.” (Interview 28, researcher, Medical Sciences)
And to these conventions, one (naturally) conforms. Stakeholders copy behavior and actions of others within their discipline, thereby causing particular behaviors and values to become conventional or normative. One of those conventions is the use of NHST and p-values. Everyone is trained with NHST and is used to applying this method. Another convention is the fact that significant results mean ‘success’, in the sense of successful research and being a successful researcher. Everyone is aware that ‘p is smaller than 0.05’ means the desired results are achieved and that publication and citation chances are increased.
P: “You want to find a significant result so badly. (…) Because people constantly think: I must find a significant result, otherwise my study is worthless.” (Focus group 4, lecturer, Medical Sciences)
Stakeholders rigidly hold on to the above-mentioned conventions and are not inclined to deviate from existing norms; they are, in other words, quite conservative . ‘We don’t know any better’ has been brought up as a valid argument by participants from various stakeholder groups to stick to current rules and conventions. Consequently, the status quo in the scientific system is being maintained.
P: “People hold on to….” I: ‘Everyone maintains the system?’ P: ‘Yes, we kind of hang to the conservative manner. This is what we know, what someone, everyone, accepts.” (Interview 17, researcher, Health Sciences)
Everyone is trained with NHST and considers it an accessible and easy to interpret method. The familiarity and perceived simplicity of NHST, user-friendly software such as SPSS and the clear cut-off value for significance are important facilitators for the use of NHST and at the same time barriers to start using alternative methods. Applied researchers stressed the importance of the accessibility of NHST as a method to test hypotheses and draw conclusions. This accessibility also justifies the use of NHST when researchers want to communicate their study results and messages in understandable ways to their readership.
P: “It is harder, also to explain, to use an alternative. So, I think, but maybe I’m overstepping, but if you want to go in that direction [alternative methods] it needs to be better facilitated for researchers. Because at the moment… I did some research, but, you know, there are those uncommon statistical packages.” (Interview 16, researcher/editor, Medical Sciences)
1 . 3 Publication pressure . Most researchers mentioned that they perceive publication pressure. This motivates them to use NHST and hope for significant results, as ‘significant p-values’ increase publication chances. They perceive a high workload and the way the scientific reward system is constructed as barriers for behavioral change pertaining to the use of statistical methods; potential negative consequences for publication and career chances prevent researchers from deviating from (un)written rules.
P: “I would like to learn it [alternative methods], but it might very well be that I will not be able to apply it, because I will not get my paper published. I find that quite tricky.” (Interview 1, Assistant Professor, Health Sciences)
2. The scientific duty
Throughout the interviews, participants reported a sense of duty in several variations. “What does it mean to be a scientific researcher?” seemed to be a question that was reflected upon during rather than prior to the interview, suggesting that many scientists had not really thought about the moral and professional obligations of being a scientist in general—let alone what that would mean for their use of NHST. Once they had given it some thought, the opinions concerning what constitutes the scientific duty varied to a large extent. Some participants attached great importance to issues such as reproducibility and transparency in scientific research and continuing education and training for researchers. For others, these topics seemed to play a less important role. A distinction was made between moral and professional obligations that participants described concerning their scientific duty.
2 . 1 Moral obligation . The moral obligation concerns issues such as doing research in a thorough and honest way, refraining from questionable research practices (QRPs) and investing in better research. It concerns tasks and activities that are not often rewarded or acknowledged.
Throughout the interviews and the focus groups, participants very frequently touched upon the responsibility they felt for doing ‘the right thing’ and making the right choice in doing research and using NHST, in particular. The extent to which they felt responsible varied among participants. When it comes to choices during doing research—for example, drawing conclusions from data—participants felt a strong sense of responsibility to do this correctly. However, when it comes to innovation and new practices, and feeling responsible for your own research, let alone improving scientific practice in general, opinions differed. This quotation from one of the focus groups illustrates that:
P1: “If you people [statisticians, methodologists] want me to improve the statistics I use in my research, then you have to hand it to me. I am not going to make any effort to improve that myself. “P3: “No. It is your responsibility as an academic to keep growing and learning and so, also to start familiarizing yourself when you notice that your statistics might need improvement.” (Focus group 2, participant 1 (PhD researcher, Medical Sciences) and 3 (Associate Professor, Health Sciences)
The sense of responsibility for improving research practices regarding the use of NHST was strongly felt and emphasized by a small group of participants. They emphasized the responsibility of the researcher to think, interpret and be critical when interpreting the p -value in NHST. It was felt that you cannot leave that up to the reader. Moreover, scrutinizing and reflecting upon research results was considered a primary responsibility of a scientist, and failing to do so, as not living up to what your job demands you to do:
P: “Yes, and if I want to be very provocative—and I often want that, because then people tend to wake up and react: then I say that hiding behind alpha.05 is just scientific laziness. Actually, it is worse: it is scientific cowardice. I would even say it is ‘relieving yourself from your duty’, but that may sound a bit harsh…” (Interview 2, Professor, Health Sciences)
These participants were convinced that scientists have a duty to keep scientific practice in general at the highest level possible.
The avoidance of questionable research practices (QRPs) was considered a means or a way to keep scientific practices high level and was often touched upon during the interviews and focus groups as being part of the scientific duty. Statisticians saw NHST as directly facilitating QRPs and providing ample examples of how the use of NHST leads to QRPs, whereas most applied researchers perceived NHST as the common way of doing research and were not aware of the risks related to QRPs. Participants did mention the violation of assumptions underlying NHST as being a QRP. Then, too, participants considered overinterpreting results as a QRP, including exaggerating the degree of significance. Although participants stated they were careful about interpreting and reporting p-values, they ‘admitted’ that statistical significance was a starting point for them. Most researchers indicated they search for information that could get their study published, which usually includes a low p-value (this also relates to the theme ‘Scientific climate’).
P: “We all know that a lot of weight is given to the p-value. So, if it is not significant, then that’s the end of it. If it ís significant, it just begins.” (Interview 5, lecturer, Psychology)
The term ‘sloppy science’ was mentioned in relation to efforts by researchers to reduce the p -value (a.k.a. p-hacking, data-dredging, and HARKing. HARKing is an acronym that refers to the questionable research question of Hypothesizing After the Results are Known. It occurs when researchers formulate a hypothesis after the data have been collected and analyzed, but make it look like it is an a priori hypothesis [ 29 ]). Preregistration and replication were mentioned as being promising solutions for some of the problems caused by NHST.
2 . 2 . Professional obligation . The theme professional obligation reflects participants’ expressions about what methodological knowledge scientists should have about NHST. In contrast moral obligations, there appeared to be some consensus about scientists’ professional obligations. Participants considered critical evaluation of research results a core professional obligation. Also, within all the stakeholder groups, participants agreed that sufficient statistical knowledge is required for using NHST, but they varied in their insights in the principles, potential and limitations of NHST. This also applied to the extent to which participants were aware of the current debate about NHST.
Participants considered critical thinking as a requirement for fulfilling their professional obligation. It specifically refers to the process of interpreting outcomes and taking all relevant contextual information into consideration. Critical thinking was not only literally referred to by participants, but also emerged by interpreting text fragments on the emphasis within their research. Researchers differed quite strongly in where the emphasis of their research outcomes should be put and what kind of information is required when reporting study results. Participants mentioned the proven effectiveness of a particular treatment, giving a summary of the research results, effect sizes, clinical relevance, p-values, or whether you have made a considerable contribution to science or society.
P: “I come back to the point where I said that people find it arbitrary to state that two points difference on a particular scale is relevant. They prefer to hide behind an alpha of 0.05, as if it is a God given truth, that it counts for one and for all. But it is just as well an invented concept and an invented guideline, an invented cut-off value, that isn’t more objective than other methods?” (Interview 2, Professor, Health Sciences)
For some participants, especially those representing funding agencies, critical thinking was primarily seen as a prerequisite for the utility of the research. The focus, when formulating the research question and interpreting the results, should be on practical relevance and the contribution the research makes to society.
The term ‘ignorance’ arose in the context of the participants’ concern regarding the level of statistical knowledge scientists and other stakeholders have versus what knowledge they should have to adequately apply statistical analysis in their research. The more statistically competent respondents in the sample felt quite strongly about how problematic the lack of knowledge about NHST is among those who regularly use it in their research, let alone the lack of knowledge about alternative methods. They felt that regularly retraining yourself in research methods is an essential part of the professional obligation one has. Applied researchers in the sample agreed that a certain level of background knowledge on NHST was required to apply it properly to research and acknowledged their own ignorance. However, they had different opinions about what level of knowledge is required. Moreover, not all of them regarded it as part of their scientific duty to be informed about all ins and outs of NHST. Some saw it as the responsibility of statisticians to actively inform them (see also the subtheme periphery). Some participants were not aware of their ignorance or stated that some of their colleagues are not aware of their ignorance, i.e., that they are unconsciously incompetent and without realizing it, poorly understood what the p-value and associated outcome measures actually mean.
P: “The worst, and I honestly think that this is the most common, is unconsciously incompetent, people don’t even understand that…” I: “Ignorance.” P: “Yes, but worse, ignorant and not even knowing you are ignorant.” (Interview 2, Professor, Health Sciences)
The lack of proper knowledge about statistical procedures was especially prevalent in the medical sciences. Participants working in or with the medical sciences all confirmed that there is little room for proper statistical training for medical students and that the level of knowledge is fairly low. NHST is often used because of its simplicity. It is especially attractive for medical PhD students because they need their PhD to get ahead in their medical career instead of pursuing a scientific career.
P: “I am not familiar with other ways of doing research. I would really like to learn, but I do not know where I could go. And I do not know whether there are better ways. So sometimes I do read studies of which I think: ‘this is something I could investigate with a completely different test. Apparently, this is also possible, but I don’t know how.’ Yes, there are courses, but I do not know what they are. And here in the medical center, a lot of research is done by medical doctors and these people have hardly been taught any statistics. Maybe they will get one or two statistics courses, they know how to do a t-test and that is about it. (…) And the courses have a very low level of statistics, so to say.” (Interview 1, Assistant Professor, Health Sciences)
Also, the term ‘ awareness ’ arose. Firstly, it refers to being conscious about the limitations of NHST. Secondly, it refers to the awareness of the ongoing discussions about NHST and more broadly, about the replication crisis. The statisticians in the sample emphasized the importance of knowing that NHST has limitations and that it cannot be considered the holy grail of data analysis. They also emphasized the importance of being aware of the debate. A certain level of awareness was considered a necessary requirement for critical thinking. There was variation in that awareness. Some participants were quite informed and were also fairly engaged in the discussion whereas others were very new to the discussion and larger contextual factors, such as the replication crisis.
I: “Are you aware of the debate going on in academia on this topic [NHST]? P: “No, I occasionally see some article sent by a colleague passing by. I have the idea that something is going on, but I do not know how the debate is conducted and how advanced it is. (Interview 6, lecturer, Psychology)
With respect to the theme, ‘the scientific duty’, participants differed to what extent they felt responsible for better and open science, for pioneering, for reviewing, and for growing and learning as a scientist. Participants had one commonality: although they strived for adherence to the norms of good research, the rampant feeling is that this is very difficult, due to the scientific climate. Consequently, participants perceive an internal conflict : a discrepancy between what they want or believe , and what they do . Participants often found themselves struggling with the responsibility they felt they had. Making the scientifically most solid choice was often difficult due to feasibility, time constraints, or certain expectations from supervisors (this is also directly related to the themes ‘Scientific climate’ and ‘Reactivity’). Thus, the scientific climate strongly influences the behavior of scientists regarding how they set their priorities and fulfill their scientific duties. The strong sense of scientific duty was perceived by some participants as a facilitator and by others as a barrier for the use of alternative methods.
3. Reactivity
A consequence of the foregoing factors is that most stakeholders have adopted a reactive attitude and behave accordingly. People are disinclined to take responsibility and await external signals and initiatives of others. This might explain why NHST is being continuously used and remains the default procedure to make inferences about population effects.
The core theme ‘reactivity’ can be explained by the following subthemes and categories:
3 . 1 Periphery . The NHST-problem resides in the periphery in several ways. First, it is a subject that is not given much priority. Secondly, some applied researchers and editors believe that methodological knowledge, as it is not their field of expertise, should not be part of their job requirement. This also applies to the NHST debate. Thirdly, and partly related to the second point, there is a lack of cooperation within and between disciplines.
The term ‘ priority’ was mentioned often when participants were asked to what extent the topic of NHST was subject of discussion in their working environment. Participants indicated that (too) little priority is given to statistics and the problems related to the subject. There is simply a lot going on in their research field and daily work, so there are always more important or urgent issues on the agenda.
P: “Discussions take place in the periphery; many people find it complicated. Or are just a little too busy.” (Interview 5, lecturer, Psychology)
As the NHST debate is not prioritized, initiatives with respect to this issue are not forthcoming. Moreover, researchers and lecturers claim there is neither time nor money available for training in statistics in general or acquiring more insight and skills with respect to (the use of) alternative methods. Busy working schedules were mentioned as an important barrier for improving statistical knowledge and skills.
P: “Well you can use your time once, so it is an issue low on the priority list.” (Focus group 5, researcher, Medical Sciences)
The NHST debate is perceived as the domain of statisticians and methodologists. Also, cooperation between different domains and domain-specific experts is perceived as complicated, as different perceptions and ways of thinking can clash. Therefore, some participants feel that separate worlds should be kept separate; put another way: stick to what you know!
P: “This part is not our job. The editorial staff, we have the assignment to ensure that it is properly written down. But the discussion about that [alternatives], that is outside our territory.” (Interview 26, editor, Medical Sciences)
Within disciplines, individuals tend to act on their own, not being aware that others are working on the same subject and that it would be worthwhile to join forces. The interviews and focus groups exposed that a modest number of participants actively try to change the current situation, but in doing that, feel like lone voices in the wilderness.
P1: “I mean, you become a lone voice in the wilderness.” P2: “Indeed, you don’t want that.” P1: “I get it, but no one listens. There is no audience.” (Focus Group 3, P1: MD, lecturer, medical Sciences, P2: editor, Medical Sciences)
To succeed at positive change, participants emphasized that it is essential that people (interdisciplinary) cooperate and join forces, rather than operate on individual levels, focusing solely on their own working environment.
The caution people show with respect to taking initiative is reenforced by the fear of encountering resistance from their working environment when one voices that change regarding the use of NHST is needed. A condition that was mentioned as essential to bring about change was tactical implementation , that is, taking very small steps. As everyone is still using NHST, taking big steps brings the risk of losing especially the more conservative people along the way. Also, the adjustment of policy, guidelines and educational programs are processes for which we need to provide time and scope.
P: “Everyone still uses it, so I think we have to be more critical, and I think we have to look at some kind of culture change, that means that we are going to let go of it (NHST) more and we will also use other tests, that in the long term will overthrow NHST. I: and what about alternatives? P: I think you should never be too fanatic in those discussion, because then you will provoke resistance. (…) That is not how it works in communication. You will touch them on a sore spot, and they will think: ‘and who are you?’ I: “and what works?” P: “well, gradualness. Tell them to use NHST, do not burn it to the ground, you do not want to touch peoples work, because it is close to their hearts. Instead, you say: ‘try to do another test next to NHST’. Be a pioneer yourself.” (Interview 5, lecturer, Psychology)
3 . 2 . Efficacy . Most participants stated they feel they are not in the position to initiate change. On the one hand, this feeling is related to their hierarchical positions within their working environments. On the other hand, the feeling is caused by the fact that statistics is perceived as a very complex field of expertise and people feel they lack sufficient knowledge and skills, especially about alternative methods.
Many participants stated they felt little sense of empowerment, or self-efficacy. The academic system is perceived as hierarchical, having an unequal balance of power. Most participants believe that it is not in their power to take a lead in innovative actions or to stand up against establishment, and think that this responsibility lies with other stakeholders, that have more status .
P: “Ideally, there would be a kind of an emergency letter from several people whose names open up doors, in which they indicate that in the medical sciences we are throwing away money because research is not being interpreted properly. Well, if these people that we listen to send such an emergency letter to the board of The Netherlands Organization for Health Research and Development [the largest Dutch funding agency for innovation and research in healthcare], I can imagine that this will initiate a discussion.” (…) I: “and with a big name you mean someone from within the science system? P: well, you know, ideally a chairman, or chairmen of the academic medical center. At that level. If they would put a letter together. Yes, that of course would have way more impact. Or some prominent medical doctors, yes, that would have more impact, than if some other person would send a letter yes.” (Interview 19, representative from funding agency, Physical Sciences)
Some participants indicated that they did try to make a difference but encountered too much resistance and therefore gave up their efforts. PhD students feel they have insufficient power to choose their own directions and make their own choices.
P: I am dependent on funding agencies and professors. In the end, I will write a grant application in that direction that gives me the greatest chance of eventually receiving that grant. Not primarily research that I think is the most optimal (…) If I know that reviewers believe the p-value is very important, well, of course I write down a method in which the p-value is central.” (Focus group 2, PhD-student, Medical Sciences)
With a sense of imperturbability, most participants accept that they cannot really change anything.
Lastly, the complexity of the subject is an obstacle for behavioral change. Statistics is perceived as a difficult subject. Participants indicate that they have a lack of knowledge and skills and that they are unsure about their own abilities. This applies to the ‘standard’ statistical methods (NHST), but to a greater extent to alternative methods. Many participants feel that they do not have the capacity to pursue a true understanding of (alternative) statistical methods.
P: “Statistics is just very hard. Time and again, research demonstrates that scientists, even the smartest, have a hard time with statistics.” (Focus group 3, PhD researcher, Psychology)
3 . 3 . Interdependency . As mentioned, participants feel they are not in a sufficiently strong position to take initiative or to behave in an anti-establishment manner. Therefore, they await external signals from people within the scientific system with more status, power, or knowledge. This can be people within their own stakeholder group, or from other stakeholder groups. As a consequence of this attitude, a situation arises in which peoples’ actions largely depend on others. That is, a complex state of interdependency evolves: scientists argue that if the reward system does not change, they are not able to alter their statistical behavior. According to researchers, editors and funding agencies are still very much focused on NHST and especially (significant) p-values, and thus, scientists wait for editors and funders to adjust their policy regarding statistics:
P: “I wrote an article and submitted it to an internal medicine journal. I only mentioned confidence intervals. Then I was asked to also write down the p-values. So, I had to do that. This is how they [editors] can use their power. They decide.” (Interview 1, Assistant Professor, Health Sciences)
Editors and funders in their turn claim they do not maintain a strict policy. Their main position is that scientists should reach consensus about the best statistical procedure, and they will then adjust their policy and guidelines.
P: “We actually believe that the research field itself should direct the quality of its research, and thus, also the discussions.” (Interview 22, representative from funding agency, Neurosciences)
Lecturers, for their part, argue that they cannot revise their educational programs due to the academic system, and university policies are adapted to NHST and p-values.
As most participants seem not to be aware of this process, a circle of interdependency arises that is difficult to break.
P: “Yes, the stupid thing about this perpetual circle is that you are educating people, let’s say in the department of cardiology. They must of course grow, and so they need to publish. If you want to publish you must meet the norms and values of the cardiology journals, so they will write down all those p-values. These people are trained and in twenty years they are on the editorial board of those journals, and then you never get rid of it [the p-value].” (Interview 18, Professor, editor, Medical Sciences)
3 . 4 . Degree of eagerness . Exerting certain behavior or behavioral change is (partly) determined by the extent to which people want to employ particular behavior, their behavioral intention [ 22 ]. Some participants indicated they are willing to change their behavior regarding the use of statistical methods, but only if it is absolutely necessary, imposed or if they think that the current conventions have too many negative consequences. Thus, true, intrinsic will-power to change behavior is lacking among these participants. Instead, they have a rather opportunistic attitude, meaning that their behavior is mostly driven by circumstances, not by principles.
P: “If tomorrow an alternative is offered by people that make that call, than I will move along. But I am not the one calling the shots on this issue.” (Interview 26, editor, Medical Sciences)
In addition, pragmatism often outweighs the perceived urgency to change. Participants argue they ‘just want to do their jobs’ and consider the practical consequences mainly in their actions. This attitude creates a certain degree of inertia. Although participants claim they are willing to change their behavior, this would contain much more than ‘doing their jobs, and thus, in the end, the NHST-debate is subject to ‘coffee talk’. People are open to discussion, but when it comes to taking action (and motivating others to do so), no one takes action.
P: “The endless analysis of your data to get something with a p-value less than 0.05… There are people that are more critical about that, and there are people that are less critical. But that is a subject for during the coffee break.” (Interview 18, professor, editor, Medical Sciences)
The goal of our study was to acquire in-depth insight into reasons why so many stakeholders from the scientific system keep using NHST as the default method to draw conclusions, despite its many well-documented drawbacks. Furthermore, we wanted to gain insight into the reasons for their reluctance to apply alternative methods. Using a theoretical framework [ 20 , 21 ], several interrelated facilitators and barriers associated with the use of NHST and alternative methods were identified. The identified factors are subsumed under three main themes: the scientific climate, the scientific duty and reactivity. The scientific climate is dominated by conventions, behavioral rules, and beliefs, of which the use of NHST and p-values is part. At the same time, stakeholders feel they have a (moral or professional) duty. For many participants, these two sides of the same coin are incompatible, leading to internal conflicts. There is a discrepancy between what participants want and what they do . As a result of these factors, the majority feels dependent on others and have thereby become reactive. Most participants are not inclined to take responsibility themselves but await action and initiatives from others. This may explain why NHST is still the standard and used by almost everyone involved.
The current study is closely related to the longstanding debate regarding NHST which recently increased to a level not seen before. In 2015, the editors of the journal ‘Basic and Applied Social Psychology’ (BASP) prohibited the use of NHST (and p-values and confidence intervals) [ 30 ]. Subsequently, in 2016, the American Statistical Association published the so-called ‘Statement on p-values’ in the American Statistician. This statement consists of critical standpoints regarding the use of NHST and p-values and warns against the abuse of the procedure. In 2019, the American Statistician devoted an entire edition to the implementation of reforms regarding the use of NHST; in more than forty articles, scientists debated statistical significance, advocated to embrace uncertainty, and suggested alternatives such as the use of s-values, False Positive Risks, reporting results as effect sizes and confidence intervals and more holistic approaches to p-values and outcome measures [ 31 ]. In addition, in the same year, several articles appeared in which an appeal was made to stop using statistical significance testing [ 32 , 33 ]. A number of counter-reactions were published [ 34 – 36 ], stating (i.e.) that banning statistical significance and, with that, abandoning clear rules for statistical analyses may create new problems with regard to statistical interpretation, study interpretations and objectivity. Also, some methodologists expressed the view that under certain circumstances the use of NHST and p-values is not problematic and can in fact provide useful answers [ 37 ]. Until recently, the NHST-debate was limited to mainly methodologists and statisticians. However, a growing number of scientists are getting involved in this lively debate and believe that a paradigm shift is desirable or even necessary.
The aforementioned publications have constructively contributed to this debate. In fact, since the publication of the special edition of the American Statistician, numerous scientific journals published editorials or revised, to a greater or lesser extent, their author guidelines [ 38 – 45 ]. Furthermore, following the American Statistical Association (ASA), the National Institute of Statistical Sciences (NISS) in the United States has also taken up the reform issue. However, real changes are still barely visible. It takes a long time before these kinds of initiatives translate into behavioral changes, and the widespread adoption by most of the scientific community is still far from accomplished. Debate alone will not lead to real changes, and therefore, our efforts to elucidate behavioral barriers and facilitators could provide a framework for potential effective initiatives that could be taken to reduce the default use of NHST. In fact, the debate could counteract behavioral change. If there is no consensus among statisticians and methodologists (the innovators), changing behavior cannot be expected from stakeholders with less statistical and methodological expertise. In other words, without agreement among innovators, early adopters might be reluctant to adopt the innovation.
Research has recently been conducted to explore the potential of behavioral change to improve Open Science behaviors. The adoption of open science behavior has increased in the last years, but uptake has been slow, due to firm barriers such as a lack of awareness about the subject, concerns about constrainment of the creative process, worries about being “scooped” and holding on to existing working practices [ 46 ]. The development regarding open science practices and the parallels these lines of research shows with the current study, might be of benefit to subserve behavioral change regarding the use of statistical methods.
The described obstacles to change behavior are related to features of both the ‘innovative idea’ and the potential adopters of the idea. First, there are characteristics of ‘the innovation’ that form barriers. The first barrier is the complexity of the innovation: most participants perceive alternative methods as difficult to understand and to use. A second barrier concerns the feasibility of trying the innovation; most people do not feel flexible about trying out or experimenting with the new idea. There is a lack of time and monetary resources to get acquainted with alternative methods (for example, by following a course). Also, the possible negative consequences of the use of alternatives (lower publications chances, the chance that the statistical method and message is too complicated for one’s readership) is holding people back from experimenting with these alternatives. And lastly, it is unclear for most participants what the visibility of the results of the new idea are. Up until now, the debate has mainly taken place among a small group of statisticians and methodologists. Many researchers are still not aware of the NHST debate and the idea to shift away from NHST and use alternative methods instead. Therefore, the question is how easily the benefits of the innovation can be made visible for a larger part of the scientific community. Thus, our study shows that, although the compatibility of the innovation is largely consistent with existing values (participants are critical about (the use of) NHST and the p-value and believe that there are better alternatives to NHST), important attributes of the innovative idea negatively affect the rate of adoption and consequently the diffusion of the innovation.
Due to the barriers mentioned above, most stakeholders do not have the intention to change their behavior and adopt the innovative idea. From the theory of planned behavior [ 21 ], it is known that behavioral intentions directly relate to performances of behaviors. The strength of the intention is shaped by attitudes, subjective norms, and perceived power. If people evaluate the suggested behavior as positive (attitude), and if they think others want them to perform the behavior (subjective norm), this leads to a stronger intention to perform that behavior. When an individual also perceives they have enough control over the behavior, they are likely to perform it. Although most participants have a positive attitude towards the behavior, or the innovative idea at stake, many participants think that others in their working environment believe that they should not perform the behavior—i.e., they do not approve of the use of alternative methods (social normative pressure). This is expressed, for example, in lower publication chances, negative judgements by supervisors or failing the requirements that are imposed by funding agencies. Thus, the perception about a particular behavior—the use of alternative methods—is negatively influenced by the (perceived) judgment of others. Moreover, we found that many participants have a low self-efficacy, meaning that there is a perceived lack of behavioral control, i.e., their perceived ability to engage in the behavior at issue is low. Also, participants feel a lack of authority (in the sense of knowledge and skills, but also power) to initiate behavioral change. The existing subjective norms and perceived behavioral control, and the negative attitudes towards performing the behavior, lead to a lower behavioral intention, and, ultimately, a lower chance of the performance of the actual behavior.
Several participants mentioned there is a need for people of stature (belonging to the group of early adopters) to take the lead and break down perceived barriers. Early adopters serve as role models and have opinion leadership, and form the next group (after the innovators, in this case statisticians and methodologists) to adopt an innovative idea [ 20 ] ( Fig 2 ). If early adopters would stand up, conveying a positive attitude towards the innovation, breaking down the described perceived barriers and facilitating the use of alternatives (for example by adjusting policy, guidelines and educational programs and making available financial resources for further training), this could positively affect the perceived social norms and self-efficacy of the early and late majority and ultimately laggards, which could ultimately lead to behavioral change among all stakeholders within the scientific community.
A strength of our study is that it is the first empirical study on views on the use of NHST, its alternatives and reasons for the prevailing use of NHST. Another strength is the method of coding which corresponds to the thematic approach from Braun & Clarke [ 47 ], which allows the researcher to move beyond just categorizing and coding the data, but also analyze how the codes are related to each other [ 47 ]. It provides a rich description of what is studied, linked to theory, but also generating new hypotheses. Moreover, two independent researchers coded all transcripts, which adds to the credibility of the study. All findings and the coding scheme were discussed by the two researchers, until consensus was reached. Also, interview results were further explored, enriched and validated by means of (mixed) focus groups. Important themes that emanated from the interviews, such as interdependency, perceptions on the scientific duty, perceived disadvantages of alternatives or the consequences of the current scientific climate, served as starting points and main subjects of the focus groups. This set-up provided more data, and more insight about the data and validation of the data. Lastly, the use of a theoretical framework [ 20 , 21 ] to develop the topic list, guide the interviews and focus groups, and guide their analysis is a strength as it provides structure to the analysis and substantiation of the results.
A limitation of this study is its sampling method. By using the network of members of the project group, and the fact that a relatively high proportion of those invited to participate refused because they thought they knew too little about the subject to be able to contribute, our sample was biased towards participants that are (somewhat) aware of the NHST debate. Our sample may also consist of people that are relatively critical towards the use of NHST, compared to the total population of researchers. It was not easy to include participants who were indifferent about or who were pro-NHST, as those were presumably less willing to make time and participate in this study. Even in our sample we found that the majority of our participants solely used NHST and perceived it as difficult if not impossible to change their behavior. These perceptions are thus probably even stronger in the target population. Another limitation, that is inherent to qualitative research, is the risk of interviewer bias. Respondents are unable, unwilling, or afraid to answer questions in good conscience, and instead provide socially desirable answers. In the context of our research, people are aware that, especially as a scientist, it does not look good to be conservative, complacent, or ignorant, or not to be open to innovation and new ideas. Therefore, some participants might have given a too favorable view of themselves. The interviewer bias can also take the other direction when values and expectations of the interviewer consciously or unconsciously influence the answers of the respondents. Although we have tried to be as neutral and objective as possible in asking questions and interpreting answers, we cannot rule out the chance that our views and opinions on the use of NHST have at times steered the respondents somewhat, potentially leading to the foregoing desirable answers.
Generalizability is a topic that is often debated in qualitative research methodology. Many researchers do not consider generalizability the purpose of qualitative research, but rather finding in-depth insights and explanations. However, this is an unjustified simplification, as generalizing of findings from qualitative research is possible. Three types of generalization in qualitative research are described: representational generalization (whether what is found in a sample can be generalized to the parent population of the sample), inferential generalization (whether findings from the study can be generalized to other settings), and theoretical generalization (where one draws theoretical statements from the findings of the study for more general application) [ 48 ]. The extent to which our results are generalizable is uncertain, as we used a theoretical sampling method, and our study was conducted exclusively in the Netherlands. We expect that the generic themes (reactivity, the scientific duty and the scientific climate) are applicable to academia in many countries across the world (inferential generalization). However, some elements, such as the Dutch educational system, will differ to a more or lesser extent from other countries (and thus can only be representationally generalized). In the Netherlands there is, for example, only one educational route after secondary school that has an academic orientation (scientific education, equivalent to the US university level education). This route consists of a bachelor’s program (typically 3 years), and a master’s program (typically 1, 2 or 3 years). Not every study program contains (compulsory) statistical courses, and statistical courses differ in depth and difficulty levels depending on the study program. Thus, not all the results will hold for other parts of the world, and further investigation is required.
Our findings demonstrate how perceived barriers to shift away from NHST set a high threshold for behavioral change and create a circle of interdependency. Behavioral change is a complex process. As ‘the stronger the intention to engage in a behavior, the more likely should be its performance’[ 21 ], further research on this subject should focus on how to influence the intention of behavior; i.e. which perceived barriers for the use of alternatives are most promising to break down in order to increase the intention for behavioral change. The present study shows that negative normative beliefs and a lack of perceived behavioral control regarding the innovation among individuals in the scientific system is a substantial problem. When social norms change in favor of the innovation, and control over the behavior increases, then the behavioral intention becomes a sufficient predictor of behavior [ 49 ]. An important follow-up question will therefore be: how can people be enthused and empowered, to ultimately take up the use of alternative methods instead of NHST? Answering this question can, in the long run, lead to the diffusion of the innovation through the scientific system as a whole.
NHST has been the leading paradigm for many decades and is deeply rooted in our science system, despite longstanding criticism. The aim of this study was to gain insight as to why we continue to use NHST. Our findings have demonstrated how perceived barriers to make a shift away from NHST set a high threshold for actual behavioral change and create a circle of interdependency between stakeholders in the scientific system. Consequently, people find themselves in a state of reactivity, which limits behavioral change with respect to the use of NHST. The next step would be to get more insight into ways to effectively remove barriers and thereby increase the intention to take a step back from NHST. A paradigm shift within a couple of years is not realistic. However, we believe that by taking small steps, one at a time, it is possible to decrease the scientific community’s strong dependence on NHST and p-values.
Supporting information
Acknowledgments.
The authors are grateful to Anja de Kruif for her contribution to the design of the study and for moderating one of the focus groups.
Data Availability
A full study protocol, including a detailed data analysis plan, was preregistered ( https://osf.io/4qg38/ ). At the start of this study, preregistration forms for qualitative studies were not developed yet. Therefore, preregistration for this study is based on an outdated form. Presently, there is a preregistration form available for qualitative studies. Information about data collection, data management, data sharing and data storage is described in a Data Management Plan. Sensitive data is stored in Darkstor, an offline archive for storing sensitive information or data (information that involves i.e., privacy or copyright). As the recordings and transcripts of the interviews and focus groups contain privacy-sensitive data, these files are archived in Darkstor and can be accessed only on request by authorized individuals (i.e., the original researcher or a research coordinator)1. Non-sensitive data is stored in DANS ( https://doi.org/10.17026/dans-2at-nzfs ) (Data Archiving and Networked Services; the Netherlands institute for permanent access to digital research resources). 1. Data requests can be send to [email protected] .
Funding Statement
This research was funded by the NWO (Nederlandse Organisatie voor Wetenschappelijk Onderzoek; Dutch Organization for Scientific Research) ( https://www.nwo.nl/ ) The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
- 1. Trafimow D. A taxonomy of model assumptions on which P is based and implications for added benefit in the sciences. International Journal of Social Research Methodology. 2019;22(6). [ Google Scholar ]
- 2. Greenland S, Senn S, Rothman K, Calin J, Poole C, Goodman S, et al. Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations Eur J Epidemiol 2016;31:337–50. doi: 10.1007/s10654-016-0149-3 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
- 3. Szucs D, Ioannidis J. When Null Hypothesis Significance Testing Is Unsuitable for Research: A Reassessment. Front Hum Neurosci. 2017;11(390):1–21. doi: 10.3389/fnhum.2017.00390 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
- 4. Trafimow D, Marks M. Using the Coefficient of Confidence to Make the Philosophical Switch From A Posteriori to A Priori Inferential Statistics. Educ Psychol Meas. 2017;77(5). doi: 10.1177/0013164416667977 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
- 5. Trafimow D, Rice S. A Test of the Null Hypothesis Significance Testing Procedure Correlation Argument. J Gen Psychol 2009;136(3):261–9. doi: 10.3200/GENP.136.3.261-270 [ DOI ] [ PubMed ] [ Google Scholar ]
- 6. Nickerson R. Null hypothesis significance testing: a review of an old and continuing controversy. Psychol Methods. 2000;5(2):241–301. doi: 10.1037/1082-989x.5.2.241 [ DOI ] [ PubMed ] [ Google Scholar ]
- 7. Goodman S, Hopkins J. Toward Evidence-Based Medical Statistics. 1: The P Value Fallacy. Ann Intern Med. 1999;130:995–1004. doi: 10.7326/0003-4819-130-12-199906150-00008 [ DOI ] [ PubMed ] [ Google Scholar ]
- 8. Nuzzo R. Statistical errors: P values, the “gold standard” of statistical validity, are not as reliable as many scientists assume Nature. 2014;506(7487):150–2. doi: 10.1038/506150a [ DOI ] [ PubMed ] [ Google Scholar ]
- 9. van de Schoot R, Verhoeven M, Hoijtink H. Bayesian evaluation of informative hypotheses in SEM using Mplus: A black bear story Eur J Dev Psychol 2013;10(1):81–98. [ Google Scholar ]
- 10. Ioannidis J. Why most published research findings are false. PLoS Med 2005;2(8):0696–701. doi: 10.1371/journal.pmed.0020124 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
- 11. Goodman S, Hopkins J. Toward Evidence-Based Medical Statistics. 2: The Bayes Factor. Ann Intern Med. 1999;130:1005–13. doi: 10.7326/0003-4819-130-12-199906150-00019 [ DOI ] [ PubMed ] [ Google Scholar ]
- 12. Goodman S. A Dirty Dozen: Twelve P-Value Misconceptions. Hematology. 2008;45:135–40. doi: 10.1053/j.seminhematol.2008.04.003 [ DOI ] [ PubMed ] [ Google Scholar ]
- 13. Van de Schoot R, Hoijtink H, Romeijn J. Moving beyond traditional null hypothesis testing: Evaluating expectations directly Front Psychol 2011;2:1–5. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
- 14. Gelman A, Carlin J, Stern H, Dunson D, Vehtari A, Rubin D. Bayesian Data Analysis: CRC Press; 2013. [ Google Scholar ]
- 15. Kass R, Raftery A. Bayes Factors. Journal of the American Statistical Association. 1995;90:773–95. [ Google Scholar ]
- 16. Hoitink H, Klugkist I, P B. Bayesian Evaluation of Informative Hypotheses. 2008. [ Google Scholar ]
- 17. Trafimow D. A frequentist alternative to significance testing, p-values, and confidence intervals. Econometrics. 2019;7(2):1–14. [ Google Scholar ]
- 18. Hoekstra R, Finch S, Hiers H, Johnson A. Probability as certainty: Dichotomous thinking and the misuse of p values. Psychon Bull Rev 2006;13(6):1033–7. doi: 10.3758/bf03213921 [ DOI ] [ PubMed ] [ Google Scholar ]
- 19. Rosendaal FR. The p-value: A clinician’s disease? European Journal of Internal Medicine. 2016;35:20–3. doi: 10.1016/j.ejim.2016.08.015 [ DOI ] [ PubMed ] [ Google Scholar ]
- 20. Rogers E. Diffusion of Innovations: Free Press; 1983. [ Google Scholar ]
- 21. Fishbein M, Ajzen I. Belief, Attitude, Intention, and Behavior: An Introduction to Theory and Research: Reading, MA: Addison-Wesley; 1975. [ Google Scholar ]
- 22. Fishbein M, Ajzen I. Predicting and Changing Behavior. The Reasoned Action Approach. New York: Psychology Press; 2010. [ Google Scholar ]
- 23. Bowen G. Grounded Theory and Sensitizing Concepts International Journal of Qualitative Methods 2006;5(5):12–23. [ Google Scholar ]
- 24. Glaser B, Barney G, Strauss A, Anselm L. The discovery of grounded theory: strategies for qualitative research Taylor & Francis Inc; 1967. [ Google Scholar ]
- 25. Boeije H. Analysis in Qualitative Research Sage Publications Ltd; 2010. [ Google Scholar ]
- 26. Joffe H, Yardley L. Content and thematic analysis. Research methods for clinical and health psychology 2004:55–68. [ Google Scholar ]
- 27. Strauss A, Corbin J. Basics of qualitative research: Grounded theory procedures and techniques 1990. [ Google Scholar ]
- 28. Haven T, van Grootel L. Preregistering qualitative research. Accountability in Research Policies and Quality Assurance. 2019;26(3):229–44. [ DOI ] [ PubMed ] [ Google Scholar ]
- 29. Kerr N. HARKing: hypothesizing after the results are known. Pers Soc Psychol Rev. 1998;2(3):196–217. doi: 10.1207/s15327957pspr0203_4 [ DOI ] [ PubMed ] [ Google Scholar ]
- 30. Trafimow D, Marks M. Editorial. Basic Appl Soc Psych. 2015;37(1):1–2. [ Google Scholar ]
- 31. Statistical Inference in the 21st Century: A world beyond p<0.05. Am Stat 2019. [ Google Scholar ]
- 32. Amrhein V, Greenland S, McShane B. Retire statistical significance. Nature. 2019;567(7748):305–7. [ DOI ] [ PubMed ] [ Google Scholar ]
- 33. Wasserstein R, Schirm A, Lazar N. Moving to a World Beyond “p < 0.05” Am Stat 2019;73:1–19. [ Google Scholar ]
- 34. Ioannidis J. The Importance of Predefined Rules and Prespecified Statistical Analyses. Do Not Abandon Significance. JAMA. 2019;321(21):2067–8. doi: 10.1001/jama.2019.4582 [ DOI ] [ PubMed ] [ Google Scholar ]
- 35. Ulrich D. The p-value wars (again). EJNMMI. 2019:2421–3. [ DOI ] [ PubMed ] [ Google Scholar ]
- 36. Haig B. Stats: retain significance testing Nature. 2019;569(7757). doi: 10.1038/d41586-019-01616-6 [ DOI ] [ PubMed ] [ Google Scholar ]
- 37. Hubbard R. Will the ASA’s Efforts to Improve Statistical Practice be Successful? Some Evidence to the Contrary. The American Statistician. 2019;73:31–5. [ Google Scholar ]
- 38. https://www.nejm.org/doi/full/10.1056/NEJMe1906559 .
- 39. https://onlinelibrary.wiley.com/doi/10.1111/pan.13721 .
- 40. https://www.sciencedirect.com/science/article/pii/S0884217519304046?via%3Dihub .
- 41. https://journals.sagepub.com/doi/full/10.1177/2398212819844167 .
- 42. https://wildlife.onlinelibrary.wiley.com/doi/full/10.1002/jwmg.21726 .
- 43. https://www.demographic-research.org/volumes/vol41/32/ .
- 44. https://asbmr.onlinelibrary.wiley.com/doi/pdf/10.1002/jbmr.3885 .
- 45. https://rss.onlinelibrary.wiley.com/doi/10.1111/j.1740-9713.2019.01295.x .
- 46. Norris E, O’Connor D. Science as behaviour: Using a behaviour change approach to increase uptake of open science. Psychology & Health 2019;34(12):1397–406. doi: 10.1080/08870446.2019.1679373 [ DOI ] [ PubMed ] [ Google Scholar ]
- 47. Braun V, Clarke V. Using thematic analysis in psychology. Qualitative Research in Psychology. 2006;3(3):77–101. [ Google Scholar ]
- 48. Ritchie J, Lewis J, McNaughton Nicholls C, Ormston R. Qualitative Research Practice. A Guide for Social Science Students and Researchers. London: SAGE Publications Ltd; 2013. [ Google Scholar ]
- 49. Glanz K, Rimer B, Viswanath KE. Health Behavior and Health Education Theory, Research and Practice: Jossey-Bass; 2008. [ Google Scholar ]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data availability statement.
- View on publisher site
- PDF (824.9 KB)
- Collections
Similar articles
Cited by other articles, links to ncbi databases.
- Download .nbib .nbib
- Format: AMA APA MLA NLM
Add to Collections

IMAGES
VIDEO
COMMENTS
H 0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. H A (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign. We interpret the hypotheses as follows: Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.
When your sample contains sufficient evidence, you can reject the null and conclude that the effect is statistically significant. Statisticians often denote the null hypothesis as H 0 or H A.. Null Hypothesis H 0: No effect exists in the population.; Alternative Hypothesis H A: The effect exists in the population.; In every study or experiment, researchers assess an effect or relationship.
Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting ...
Abstract: "null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences to investigate if an effect is likely". No, NHST is the method to test the hypothesis of no effect. I agree - yet people use it to investigate (not test) if an effect is likely. The issue here is wording.
HYPOTHESIS TESTING. A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the "alternate" hypothesis, and the opposite ...
There are 5 main steps in hypothesis testing: State your research hypothesis as a null hypothesis and alternate hypothesis (H o) and (H a or H 1). Collect data in a way designed to test the hypothesis. Perform an appropriate statistical test. Decide whether to reject or fail to reject your null hypothesis.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
In this blog post, we get insights into explaining hypothesis testing with real-world examples and how it can be applied in medical settings. Understanding Hypothesis Testing. Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating a null hypothesis (H0) and an ...
The null hypothesis significance test (NHST) is the most frequently used statistical method, although its inferential validity has been widely criticized since its introduction. In 1988, the International Committee of Medical Journal Editors (ICMJE) warned against sole reliance on NHST to substantiate study conclusions and suggested supplementary use of confidence intervals (CI).
The null hypothesis (H0) answers "No, there's no effect in the population.". The alternative hypothesis (Ha) answers "Yes, there is an effect in the population.". The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
Examples of the Null Hypothesis. To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this. Question.
Hypothesis testing Hypothesis testing, also known as statistical inference or significance testing, involves testing a specified hypothesized condition for a population's parameter. This condition is best described as the null hypothesis. For example, in a clinical trial of a new anti-hypertensive drug, the null hypothesis would state
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise.. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength ...
The null hypothesis is the hypothesis to be tested. It is denoted by the symbol H 0. It is also known as the hypothesis of no difference. The null hypothesis is set up with the sole purpose of efforts to knock it down. In the testing of hypothesis, the null hypothesis is either rejected (knocked down) or not rejected (upheld). If the null ...
The first step in testing hypotheses is the transformation of the research question into a null hypothesis, H 0, and an alternative hypothesis, H A. 6 The null and alternative hypotheses are concise statements, usually in mathematical form, of 2 possible versions of "truth" about the relationship between the predictor of interest and the outcome in the population.
In hypothesis testing, the research question of interest is simplified into one of two possible hypothesis types: the null hypothesis, denoted H 0, or the research hypothesis (sometimes called the alternative hypothesis), denoted H 1.In most cases, it is easier to reject a statement that is false (null hypothesis); therefore, we generally assume the opposite of our research question of interest.
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
23.1 How Hypothesis Tests Are Reported in the News 1. Determine the null hypothesis and the alternative hypothesis. 2. Collect and summarize the data into a test statistic. 3. Use the test statistic to determine the p-value. 4. The result is statistically significant if the p-value is less than or equal to the level of significance.
10.1 - Setting the Hypotheses: Examples. A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or ...
H a: The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0. Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
The null hypothesis significance test (NHST) is the most frequently used statistical method, although its inferential validity has been widely criticized since its introduction. In 1988, the International Committee of Medical Journal Editors (ICMJE) warned against sole reliance on NHST to substantiate study conclusions and suggested ...
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There's no effect in the population. Alternative hypothesis (HA): There's an effect in the population. The effect is usually the effect of the independent variable on the dependent ...
Madalynn Grimsley February 28, 2024 BUS 271, Business Statistics Concept Questions: Module 4 (Sampling and Hypothesis Testing) 1. Explain the purpose of Hypothesis Testing. Hypothesis testing is used when a statistician makes statistical inferences about populations based on sample taken and makes a decision based on those inferences. It involves collecting data from a sample and evaluating ...
Assessing statistical significance by means of contrasting the data with the null hypothesis is called Null Hypothesis Significance Testing (NHST). NHST is the best known and most widely used statistical procedure for making inferences about population effects. The procedure has become the prevailing paradigm in empirical science [3], and ...