example of hypothesis testing data

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.3 hypothesis testing examples.

• Example: Right-Tailed Test
• Example: Left-Tailed Test
• Example: Two-Tailed Test

Brinell Hardness Scores

An engineer measured the Brinell hardness of 25 pieces of ductile iron that were subcritically annealed. The resulting data were:

The engineer hypothesized that the mean Brinell hardness of all such ductile iron pieces is greater than 170. Therefore, he was interested in testing the hypotheses:

H 0 : μ = 170 H A : μ > 170

The engineer entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

Descriptive Statistics

$\mu$: mean of Brinelli

Null hypothesis    H₀: $\mu$ = 170 Alternative hypothesis    H₁: $\mu$ > 170

The output tells us that the average Brinell hardness of the n = 25 pieces of ductile iron was 172.52 with a standard deviation of 10.31. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 10.31 by the square root of n = 25, is 2.06). The test statistic t * is 1.22, and the P -value is 0.117.

If the engineer set his significance level α at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were greater than 1.7109 (determined using statistical software or a t -table):

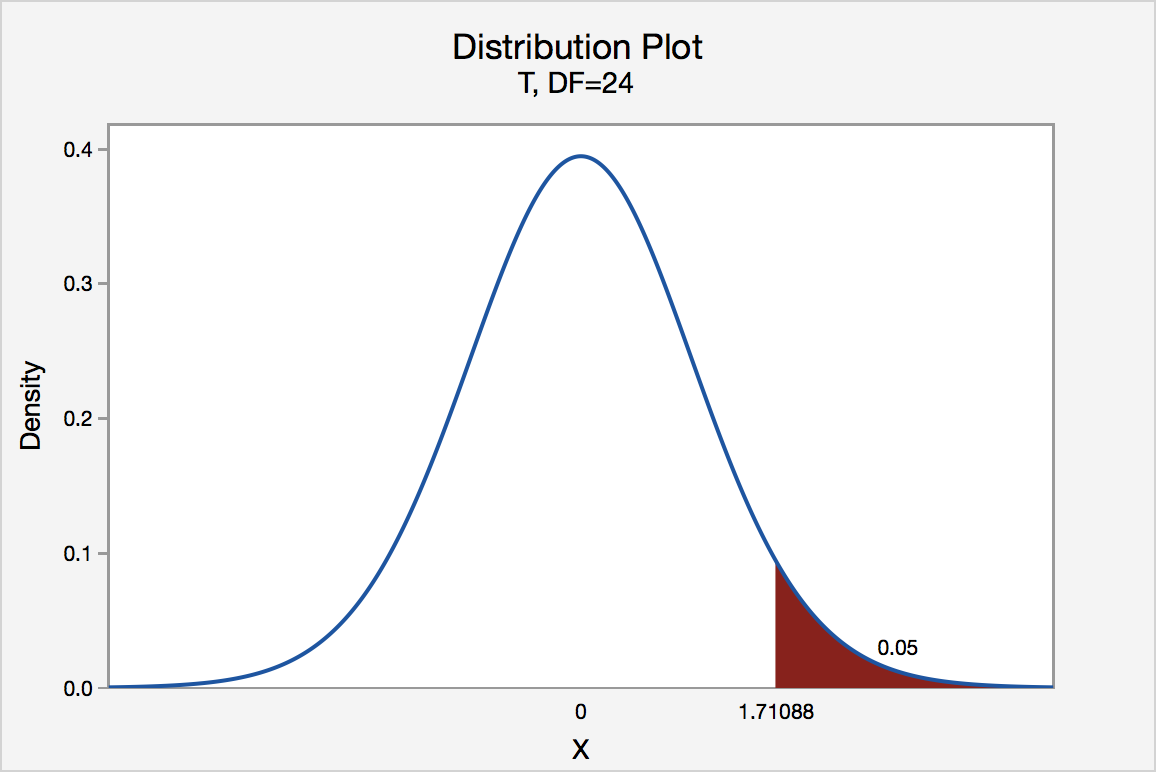
Since the engineer's test statistic, t * = 1.22, is not greater than 1.7109, the engineer fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

If the engineer used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 24 curve and to the right of the test statistic t * = 1.22:

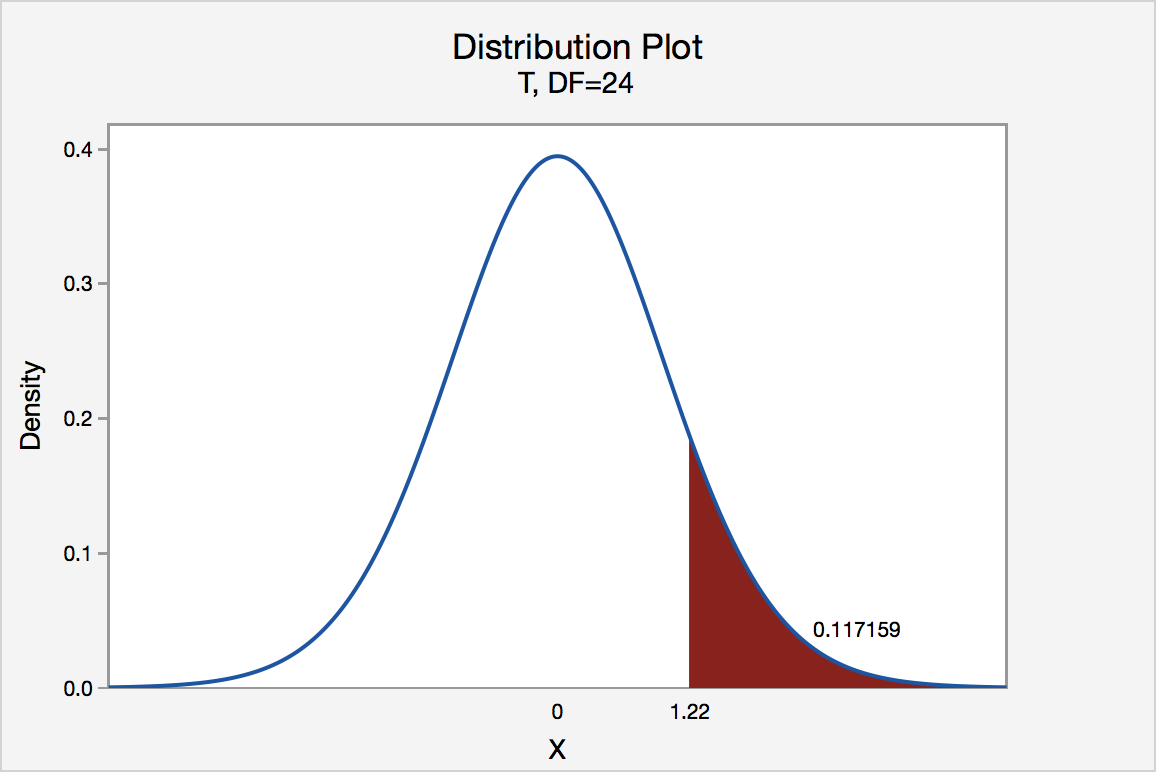
In the output above, Minitab reports that the P -value is 0.117. Since the P -value, 0.117, is greater than \(\alpha\) = 0.05, the engineer fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

Note that the engineer obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Height of Sunflowers

A biologist was interested in determining whether sunflower seedlings treated with an extract from Vinca minor roots resulted in a lower average height of sunflower seedlings than the standard height of 15.7 cm. The biologist treated a random sample of n = 33 seedlings with the extract and subsequently obtained the following heights:

The biologist's hypotheses are:

H 0 : μ = 15.7 H A : μ < 15.7

The biologist entered her data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. She obtained the following output:

$\mu$: mean of Height

Null hypothesis    H₀: $\mu$ = 15.7 Alternative hypothesis    H₁: $\mu$ < 15.7

The output tells us that the average height of the n = 33 sunflower seedlings was 13.664 with a standard deviation of 2.544. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 13.664 by the square root of n = 33, is 0.443). The test statistic t * is -4.60, and the P -value, 0.000, is to three decimal places.

Minitab Note. Minitab will always report P -values to only 3 decimal places. If Minitab reports the P -value as 0.000, it really means that the P -value is 0.000....something. Throughout this course (and your future research!), when you see that Minitab reports the P -value as 0.000, you should report the P -value as being "< 0.001."

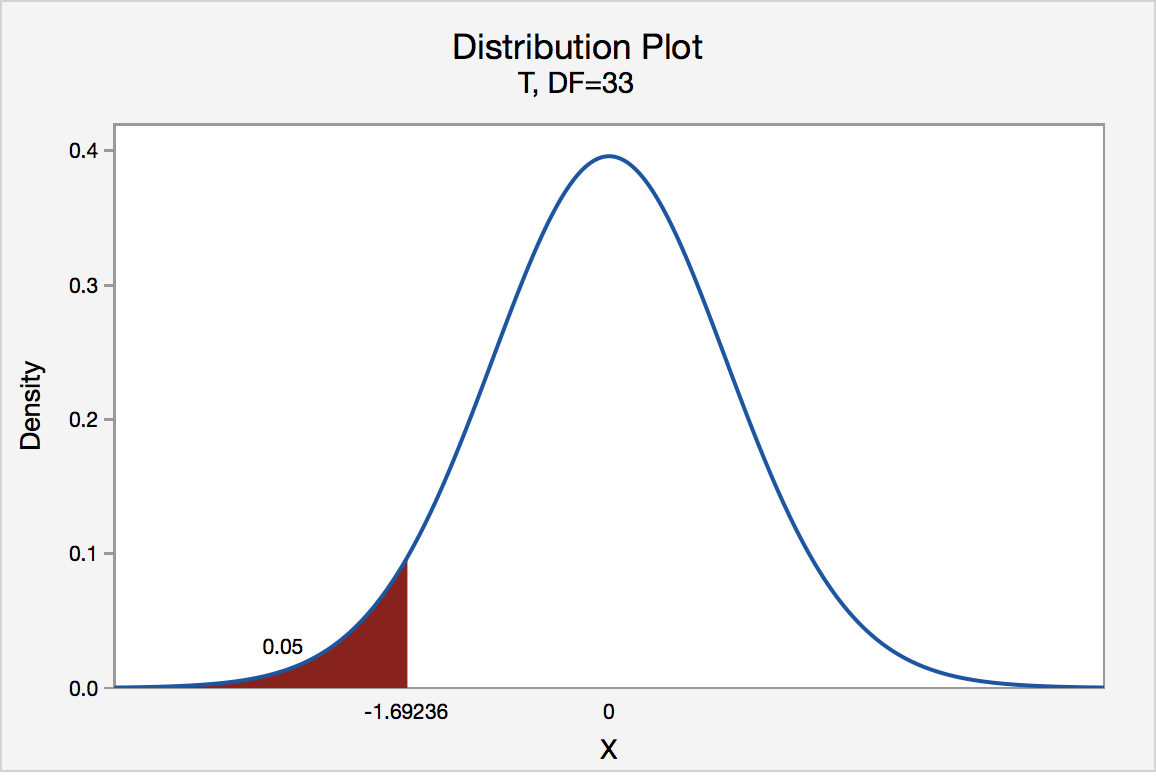
If the biologist set her significance level \(\alpha\) at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t * were less than -1.6939 (determined using statistical software or a t -table):s-3-3

Since the biologist's test statistic, t * = -4.60, is less than -1.6939, the biologist rejects the null hypothesis. That is, the test statistic falls in the "critical region." There is sufficient evidence, at the α = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

If the biologist used the P -value approach to conduct her hypothesis test, she would determine the area under a t n - 1 = t 32 curve and to the left of the test statistic t * = -4.60:

In the output above, Minitab reports that the P -value is 0.000, which we take to mean < 0.001. Since the P -value is less than 0.001, it is clearly less than \(\alpha\) = 0.05, and the biologist rejects the null hypothesis. There is sufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

Note again that the biologist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Gum Thickness

A manufacturer claims that the thickness of the spearmint gum it produces is 7.5 one-hundredths of an inch. A quality control specialist regularly checks this claim. On one production run, he took a random sample of n = 10 pieces of gum and measured their thickness. He obtained:

The quality control specialist's hypotheses are:

H 0 : μ = 7.5 H A : μ ≠ 7.5

The quality control specialist entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

$\mu$: mean of Thickness

Null hypothesis    H₀: $\mu$ = 7.5 Alternative hypothesis    H₁: $\mu \ne$ 7.5

The output tells us that the average thickness of the n = 10 pieces of gums was 7.55 one-hundredths of an inch with a standard deviation of 0.1027. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 0.1027 by the square root of n = 10, is 0.0325). The test statistic t * is 1.54, and the P -value is 0.158.

If the quality control specialist sets his significance level \(\alpha\) at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were less than -2.2616 or greater than 2.2616 (determined using statistical software or a t -table):

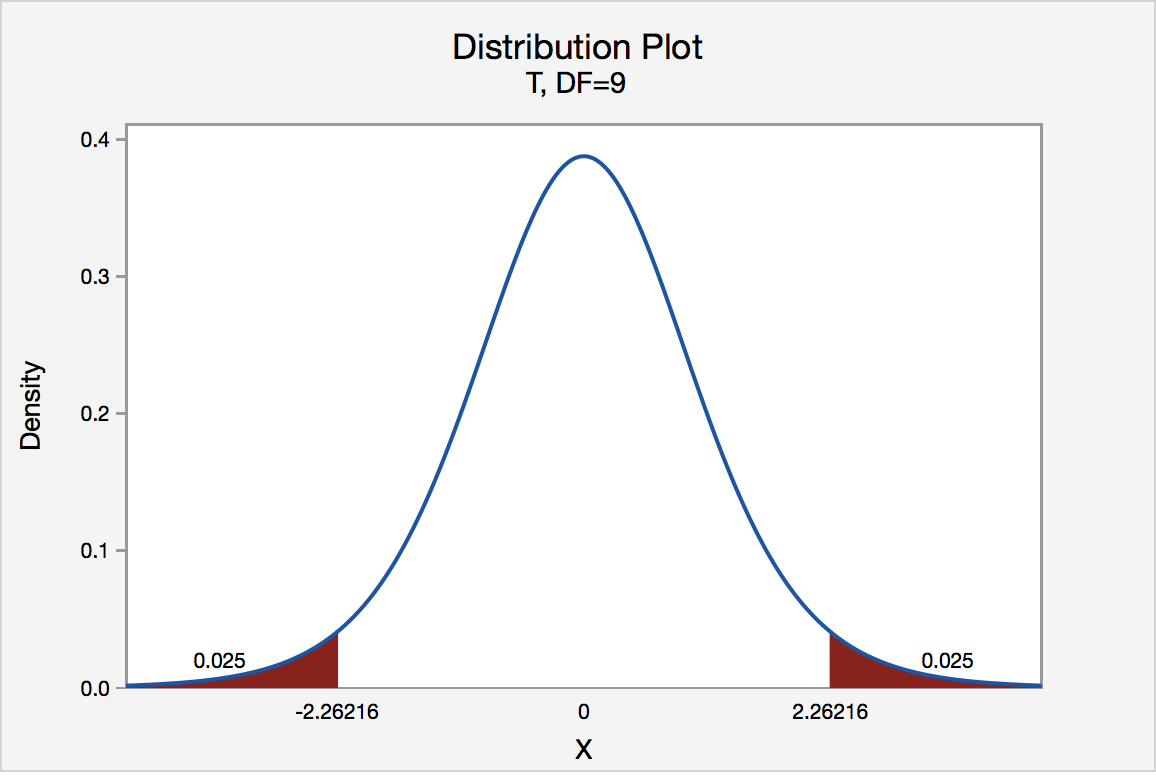
Since the quality control specialist's test statistic, t * = 1.54, is not less than -2.2616 nor greater than 2.2616, the quality control specialist fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all of the manufacturer's spearmint gum differs from 7.5 one-hundredths of an inch.

If the quality control specialist used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 9 curve, to the right of 1.54 and to the left of -1.54:

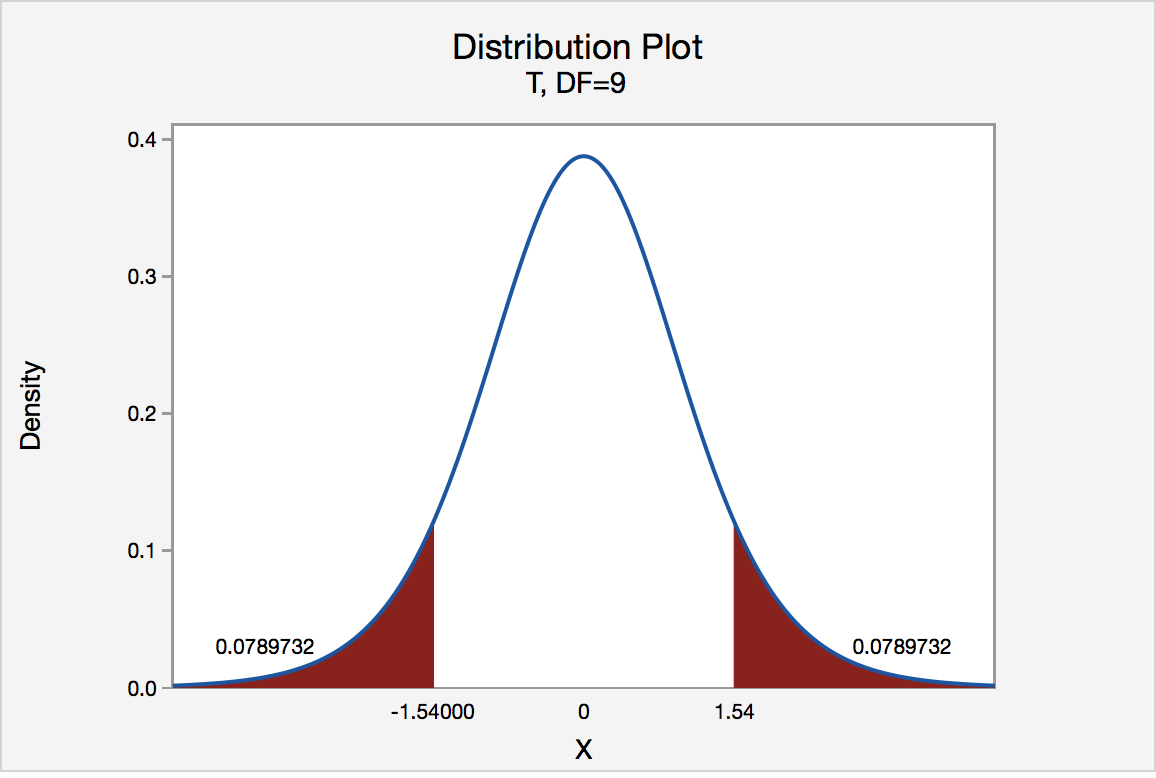
In the output above, Minitab reports that the P -value is 0.158. Since the P -value, 0.158, is greater than \(\alpha\) = 0.05, the quality control specialist fails to reject the null hypothesis. There is insufficient evidence, at the \(\alpha\) = 0.05 level, to conclude that the mean thickness of all pieces of spearmint gum differs from 7.5 one-hundredths of an inch.

Note that the quality control specialist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

In our review of hypothesis tests, we have focused on just one particular hypothesis test, namely that concerning the population mean \(\mu\). The important thing to recognize is that the topics discussed here — the general idea of hypothesis tests, errors in hypothesis testing, the critical value approach, and the P -value approach — generally extend to all of the hypothesis tests you will encounter.

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics beginner's guide.

Lesson 10 of 24 By Avijeet Biswal

Table of Contents

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life - 

• A teacher assumes that 60% of his college's students come from lower-middle-class families.
• A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

• Here, x̅ is the sample mean,
• μ0 is the population mean,
• σ is the standard deviation,
• n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average. 

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

 We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results 

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square 

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

• The null hypothesis is (H0 <= 90) or less change.
• A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true]. 

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales.  If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

• Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
• Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
• Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
• Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

• It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
• Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
• Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
• Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

• One-sample test: Used to compare a sample to a known value or a hypothesized value.
• Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
• Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
• Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
• ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

• Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
• Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
• Collect and analyze data: Gather and process the sample data.
• Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
• Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
• Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

• One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
• Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

• Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
• Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
• Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

Hypothesis Testing Steps & Examples

Table of Contents

What is a Hypothesis testing?

As per the definition from Oxford languages, a hypothesis is a supposition or proposed explanation made on the basis of limited evidence as a starting point for further investigation. As per the Dictionary page on Hypothesis , Hypothesis means a proposition or set of propositions, set forth as an explanation for the occurrence of some specified group of phenomena, either asserted merely as a provisional conjecture to guide investigation (working hypothesis) or accepted as highly probable in the light of established facts.

The hypothesis can be defined as the claim that can either be related to the truth about something that exists in the world, or, truth about something that’s needs to be established a fresh . In simple words, another word for the hypothesis is the “claim” . Until the claim is proven to be true, it is called the hypothesis. Once the claim is proved, it becomes the new truth or new knowledge about the thing. For example , let’s say that a claim is made that students studying for more than 6 hours a day gets more than 90% of marks in their examination. Now, this is just a claim or a hypothesis and not the truth in the real world. However, in order for the claim to become the truth for widespread adoption, it needs to be proved using pieces of evidence, e.g., data.  In order to reject this claim or otherwise, one needs to do some empirical analysis by gathering data samples and evaluating the claim. The process of gathering data and evaluating the claims or hypotheses with the goal to reject or otherwise (failing to reject) can be called as hypothesis testing . Note the wordings – “failing to reject”. It means that we don’t have enough evidence to reject the claim. Thus, until the time that new evidence comes up, the claim can be considered the truth. There are different techniques to test the hypothesis in order to reach the conclusion of whether the hypothesis can be used to represent the truth of the world.

One must note that the hypothesis testing never constitutes a proof that the hypothesis is absolute truth based on the observations. It only provides added support to consider the hypothesis as truth until the time that new evidences can against the hypotheses can be gathered. We can never be 100% sure about truth related to those hypotheses based on the hypothesis testing.

Simply speaking, hypothesis testing is a framework that can be used to assert whether the claim or the hypothesis made about a real-world/real-life event can be seen as the truth or otherwise based on the given data (evidences).

Hypothesis Testing Examples

Before we get ahead and start understanding more details about hypothesis and hypothesis testing steps, lets take a look at some  real-world examples  of how to think about hypothesis and hypothesis testing when dealing with real-world problems :

• Customers are churning because they ain’t getting response to their complaints or issues
• Customers are churning because there are other competitive services in the market which are providing these services at lower cost.
• Customers are churning because there are other competitive services which are providing more services at the same cost.
• It is claimed that a 500 gm sugar packet for a particular brand, say XYZA, contains sugar of less than 500 gm, say around 480gm.  Can this claim be taken as truth? How do we know that this claim is true? This is a hypothesis until proved.
• A group of doctors claims that quitting smoking increases lifespan. Can this claim be taken as new truth? The hypothesis is that quitting smoking results in an increase in lifespan.
• It is claimed that brisk walking for half an hour every day reverses diabetes. In order to accept this in your lifestyle, you may need evidence that supports this claim or hypothesis.
• It is claimed that doing Pranayama yoga for 30 minutes a day can help in easing stress by 50%. This can be termed as hypothesis and would require testing / validation for it to be established as a truth and recommended for widespread adoption.
• One common real-life example of hypothesis testing is election polling. In order to predict the outcome of an election, pollsters take a sample of the population and ask them who they plan to vote for. They then use hypothesis testing to assess whether their sample is representative of the population as a whole. If the results of the hypothesis test are significant, it means that the sample is representative and that the poll can be used to predict the outcome of the election. However, if the results are not significant, it means that the sample is not representative and that the poll should not be used to make predictions.
• Machine learning models make predictions based on the input data. Each of the machine learning model representing a function approximation can be taken as a hypothesis. All different models constitute what is called as hypothesis space .
• As part of a linear regression machine learning model , it is claimed that there is a relationship between the response variables and predictor variables? Can this hypothesis or claim be taken as truth? Let’s say, the hypothesis is that the housing price depends upon the average income of people already staying in the locality. How true is this hypothesis or claim? The relationship between response variable and each of the predictor variables can be evaluated using T-test and T-statistics .
• For linear regression model , one of the hypothesis is that there is no relationship between the response variable and any of the predictor variables. Thus, if b1, b2, b3 are three parameters, all of them is equal to 0. b1 = b2 = b3 = 0. This is where one performs F-test and use F-statistics to test this hypothesis.

You may note different hypotheses which are listed above. The next step would be validate some of these hypotheses. This is where data scientists will come into picture. One or more data scientists may be asked to work on different hypotheses. This would result in these data scientists looking for appropriate data related to the hypothesis they are working. This section will be detailed out in near future.

State the Hypothesis to begin Hypothesis Testing

The first step to hypothesis testing is defining or stating a hypothesis. Before the hypothesis can be tested, we need to formulate the hypothesis in terms of mathematical expressions. There are two important aspects to pay attention to, prior to the formulation of the hypothesis. The following represents different types of hypothesis that could be put to hypothesis testing:

• Claim made against the well-established fact : The case in which a fact is well-established, or accepted as truth or “knowledge” and a new claim is made about this well-established fact. For example , when you buy a packet of 500 gm of sugar, you assume that the packet does contain at the minimum 500 gm of sugar and not any less, based on the label of 500 gm on the packet. In this case, the fact is given or assumed to be the truth. A new claim can be made that the 500 gm sugar contains sugar weighing less than 500 gm. This claim needs to be tested before it is accepted as truth. Such cases could be considered for hypothesis testing if this is claimed that the assumption or the default state of being is not true. The claim to be established as new truth can be stated as “alternate hypothesis”. The opposite state can be stated as “null hypothesis”. Here the claim that the 500 gm packet consists of sugar less than 500 grams would be stated as alternate hypothesis. The opposite state which is the sugar packet consists 500 gm is null hypothesis.
• Claim to establish the new truth : The case in which there is some claim made about the reality that exists in the world (fact). For example , the fact that the housing price depends upon the average income of people already staying in the locality can be considered as a claim and not assumed to be true. Another example could be the claim that running 5 miles a day would result in a reduction of 10 kg of weight within a month. There could be varied such claims which when required to be proved as true have to go through hypothesis testing. The claim to be established as new truth can be stated as “alternate hypothesis”. The opposite state can be stated as “null hypothesis”. Running 5 miles a day would result in reduction of 10 kg within a month would be stated as alternate hypothesis.

Based on the above considerations, the following hypothesis can be stated for doing hypothesis testing.

• The packet of 500 gm of sugar contains sugar of weight less than 500 gm. (Claim made against the established fact). This is a new knowledge which requires hypothesis testing to get established and acted upon.
• The housing price depends upon the average income of the people staying in the locality. This is a new knowledge which requires hypothesis testing to get established and acted upon.
• Running 5 miles a day results in a reduction of 10 kg of weight within a month. This is a new knowledge which requires hypothesis testing to get established for widespread adoption.

Formulate Null & Alternate Hypothesis as Next Step

Once the hypothesis is defined or stated, the next step is to formulate the null and alternate hypothesis in order to begin hypothesis testing as described above.

What is a null hypothesis?

In the case where the given statement is a well-established fact or default state of being in the real world, one can call it a null hypothesis (in the simpler word, nothing new). Well-established facts don’t need any hypothesis testing and hence can be called the null hypothesis. In cases, when there are any new claims made which is not well established in the real world, the null hypothesis can be thought of as the default state or opposite state of that claim. For example , in the previous section, the claim or hypothesis is made that the students studying for more than 6 hours a day gets more than 90% of marks in their examination. The null hypothesis, in this case, will be that the claim is not true or real. The null hypothesis can be stated that there is no relationship or association between the students reading more than 6 hours a day and they getting 90% of the marks. Any occurrence is only a chance occurrence. Another example of hypothesis is when somebody is alleged that they have performed a crime.

Null hypothesis is denoted by letter H with 0, e.g., [latex]H_0[/latex]

What is an alternate hypothesis?

When the given statement is a claim (unexpected event in the real world) and not yet proven, one can call/formulate it as an alternate hypothesis and accordingly define a null hypothesis which is the opposite state of the hypothesis. The alternate hypothesis is a new knowledge or truth that needs to be established. In simple words, the hypothesis or claim that needs to be tested against reality in the real world can be termed the alternate hypothesis. In order to reach a conclusion that the claim (alternate hypothesis) can be considered the new knowledge or truth (based on the available evidence), it would be important to reject the null hypothesis. It should be noted that null and alternate hypotheses are mutually exclusive and at the same time asymmetric. In the example given in the previous section, the claim that the students studying for more than 6 hours get more than 90% of marks can be termed as the alternate hypothesis.

Alternate hypothesis is denoted with H subscript a, e.g., [latex]H_a[/latex]

Once the hypothesis is formulated as null([latex]H_0[/latex]) and alternate hypothesis ([latex]H_a[/latex]), there are two possible outcomes that can happen from hypothesis testing. These outcomes are the following:

• Reject the null hypothesis : There is enough evidence based on which one can reject the null hypothesis. Let’s understand this with the help of an example provided earlier in this section. The null hypothesis is that there is no relationship between the students studying more than 6 hours a day and getting more than 90% marks. In a sample of 30 students studying more than 6 hours a day, it was found that they scored 91% marks. Given that the null hypothesis is true, this kind of hypothesis testing result will be highly unlikely. This kind of result can’t happen by chance. That would mean that the claim can be taken as the new truth or new knowledge in the real world. One can go and take further samples of 30 students to perform some more testing to validate the hypothesis. If similar results show up with other tests, it can be said with very high confidence that there is enough evidence to reject the null hypothesis that there is no relationship between the students studying more than 6 hours a day and getting more than 90% marks. In such cases, one can go to accept the claim as new truth that the students studying more than 6 hours a day get more than 90% marks. The hypothesis can be considered the new truth until the time that new tests provide evidence against this claim.
• Fail to reject the null hypothesis : There is not enough evidence-based on which one can reject the null hypothesis (well-established fact or reality). Thus, one would fail to reject the null hypothesis. In a sample of 30 students studying more than 6 hours a day, the students were found to score 75%. Given that the null hypothesis is true, this kind of result is fairly likely or expected. With the given sample, one can’t reject the null hypothesis that there is no relationship between the students studying more than 6 hours a day and getting more than 90% marks.

Examples of formulating the null and alternate hypothesis

The following are some examples of the null and alternate hypothesis.

Hypothesis Testing Steps

Here is the diagram which represents the workflow of Hypothesis Testing.

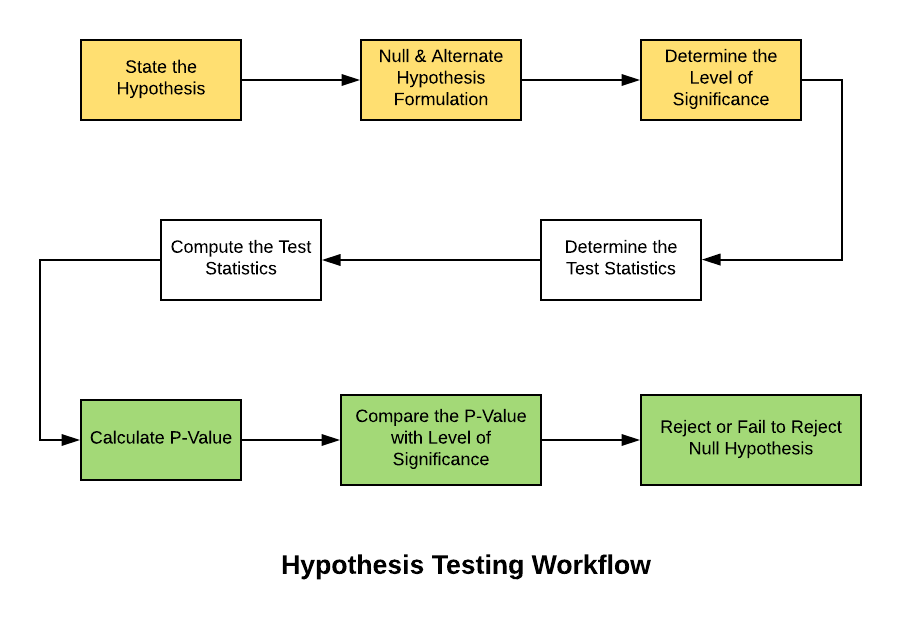
Figure 1. Hypothesis Testing Steps

Based on the above, the following are some of the  steps to be taken when doing hypothesis testing:

• State the hypothesis : First and foremost, the hypothesis needs to be stated. The hypothesis could either be the statement that is assumed to be true or the claim which is made to be true.
• Formulate the hypothesis : This step requires one to identify the Null and Alternate hypotheses or in simple words, formulate the hypothesis. Take an example of the canned sauce weighing 500 gm as the Null Hypothesis.
• Set the criteria for a decision : Identify test statistics that could be used to assess the Null Hypothesis. The test statistics with the above example would be the average weight of the sugar packet, and t-statistics would be used to determine the P-value. For different kinds of problems, different kinds of statistics including Z-statistics, T-statistics, F-statistics, etc can be used.
• Identify the level of significance (alpha) : Before starting the hypothesis testing, one would be required to set the significance level (also called as  alpha ) which represents the value for which a P-value less than or equal to  alpha  is considered statistically significant. Typical values of  alpha  are 0.1, 0.05, and 0.01. In case the P-value is evaluated as statistically significant, the null hypothesis is rejected. In case, the P-value is more than the  alpha  value, the null hypothesis is failed to be rejected.
• Compute the test statistics : Next step is to calculate the test statistics (z-test, t-test, f-test, etc) to determine the P-value. If the sample size is more than 30, it is recommended to use z-statistics. Otherwise, t-statistics could be used. In the current example where 20 packets of canned sauce is selected for hypothesis testing, t-statistics will be calculated for the mean value of 505 gm (sample mean). The t-statistics would then be calculated as the difference of 505 gm (sample mean) and the population means (500 gm) divided by the sample standard deviation divided by the square root of sample size (20).
• Calculate the P-value of the test statistics : Once the test statistics have been calculated, find the P-value using either of t-table or a z-table. P-value is the probability of obtaining a test statistic (t-score or z-score) equal to or more extreme than the result obtained from the sample data, given that the null hypothesis H0 is true.
• Compare P-value with the level of significance : The significance level is set as the allowable range within which if the value appears, one will be failed to reject the Null Hypothesis. This region is also called as Non-rejection region . The value of alpha is compared with the p-value. If the p-value is less than the significance level, the test is statistically significant and hence, the null hypothesis will be rejected.

P-Value: Key to Statistical Hypothesis Testing

Once you formulate the hypotheses, there is the need to test those hypotheses. Meaning, say that the null hypothesis is stated as the statement that housing price does not depend upon the average income of people staying in the locality, it would be required to be tested by taking samples of housing prices and, based on the test results, this Null hypothesis could either be rejected or failed to be rejected . In hypothesis testing, the following two are the outcomes:

• Reject the Null hypothesis
• Fail to Reject the Null hypothesis

Take the above example of the sugar packet weighing 500 gm. The Null hypothesis is set as the statement that the sugar packet weighs 500 gm. After taking a sample of 20 sugar packets and testing/taking its weight, it was found that the average weight of the sugar packets came to 495 gm. The test statistics (t-statistics) were calculated for this sample and the P-value was determined. Let’s say the P-value was found to be 15%. Assuming that the level of significance is selected to be 5%, the test statistic is not statistically significant (P-value > 5%) and thus, the null hypothesis fails to get rejected. Thus, one could safely conclude that the sugar packet does weigh 500 gm. However, if the average weight of canned sauce would have found to be 465 gm, this is way beyond/away from the mean value of 500 gm and one could have ended up rejecting the Null Hypothesis based on the P-value .

Hypothesis Testing for Problem Analysis & Solution Implementation

Hypothesis testing can be applied in both problem analysis and solution implementation. The following represents method on how you can apply hypothesis testing technique for both problem and solution space:

• Problem Analysis : Hypothesis testing is a systematic way to validate assumptions or educated guesses during problem analysis. It allows for a structured investigation into the nature of a problem and its potential root causes. In this process, a null hypothesis and an alternative hypothesis are usually defined. The null hypothesis generally asserts that no significant change or effect exists, while the alternative hypothesis posits the opposite. Through controlled experiments, data collection, or statistical analysis, these hypotheses are then tested to determine their validity. For example, if a software company notices a sudden increase in user churn rate, they might hypothesize that the recent update to their application is the root cause. The null hypothesis could be that the update has no effect on churn rate, while the alternative hypothesis would assert that the update significantly impacts the churn rate. By analyzing user behavior and feedback before and after the update, and perhaps running A/B tests where one user group has the update and another doesn’t, the company can test these hypotheses. If the alternative hypothesis is confirmed, the company can then focus on identifying specific issues in the update that may be causing the increased churn, thereby moving closer to a solution.
• Solution Implementation : Hypothesis testing can also be a valuable tool during the solution implementation phase, serving as a method to evaluate the effectiveness of proposed remedies. By setting up a specific hypothesis about the expected outcome of a solution, organizations can create targeted metrics and KPIs to measure success. For example, if a retail business is facing low customer retention rates, they might implement a loyalty program as a solution. The hypothesis could be that introducing a loyalty program will increase customer retention by at least 15% within six months. The null hypothesis would state that the loyalty program has no significant effect on retention rates. To test this, the company can compare retention metrics from before and after the program’s implementation, possibly even setting up control groups for more robust analysis. By applying statistical tests to this data, the company can determine whether their hypothesis is confirmed or refuted, thereby gauging the effectiveness of their solution and making data-driven decisions for future actions.
• Tests of Significance
• Hypothesis testing for the Mean
• z-statistics vs t-statistics (Khan Academy)

Hypothesis testing quiz

The claim that needs to be established is set as ____________, the outcome of hypothesis testing is _________.

Please select 2 correct answers

P-value is defined as the probability of obtaining the result as extreme given the null hypothesis is true

There is a claim that doing pranayama yoga results in reversing diabetes. which of the following is true about null hypothesis.

In this post, you learned about hypothesis testing and related nuances such as the null and alternate hypothesis formulation techniques, ways to go about doing hypothesis testing etc. In data science, one of the reasons why one needs to understand the concepts of hypothesis testing is the need to verify the relationship between the dependent (response) and independent (predictor) variables. One would, thus, need to understand the related concepts such as hypothesis formulation into null and alternate hypothesis, level of significance, test statistics calculation, P-value, etc. Given that the relationship between dependent and independent variables is a sort of hypothesis or claim , the null hypothesis could be set as the scenario where there is no relationship between dependent and independent variables.

Recent Posts

• Pricing Analytics in Banking: Strategies, Examples - May 15, 2024
• How to Learn Effectively: A Holistic Approach - May 13, 2024
• How to Choose Right Statistical Tests: Examples - May 13, 2024

Ajitesh Kumar

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• Search for:
• Excellence Awaits: IITs, NITs & IIITs Journey

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Pricing Analytics in Banking: Strategies, Examples
• How to Learn Effectively: A Holistic Approach
• How to Choose Right Statistical Tests: Examples
• Data Lakehouses Fundamentals & Examples
• Machine Learning Lifecycle: Data to Deployment Example

Data Science / AI Trends

• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable
• • Machine learning in finance

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading Change and Organizational Renewal
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

A Beginner’s Guide to Hypothesis Testing in Business

• 30 Mar 2021

Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.

If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.

Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.

Access your free e-book today.

What Is Hypothesis Testing?

To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.

A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”

Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.

Hypothesis Testing in Business

When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.

The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.

As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.

In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.

Related: 9 Fundamental Data Science Skills for Business Professionals

Key Considerations for Hypothesis Testing

1. alternative hypothesis and null hypothesis.

In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.

For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.

In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”

The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.

Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.

2. Significance Level and P-Value

Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.

In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.

3. One-Sided vs. Two-Sided Testing

When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.

Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

4. Sampling

To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.

A survey involves asking a series of questions to a random population sample and recording self-reported responses.

Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.

Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

Learn How to Perform Hypothesis Testing

Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.

If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.

Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.E: Hypothesis Testing with One Sample (Exercises)

• Last updated
• Save as PDF
• Page ID 1146

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

These are homework exercises to accompany the Textmap created for "Introductory Statistics" by OpenStax.

9.1: Introduction

9.2: null and alternative hypotheses.

Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.

State the null hypothesis, \(H_{0}\), and the alternative hypothesis. \(H_{a}\), in terms of the appropriate parameter \((\mu \text{or} p)\).

• The mean number of years Americans work before retiring is 34.
• At most 60% of Americans vote in presidential elections.
• The mean starting salary for San Jose State University graduates is at least $100,000 per year.
• Twenty-nine percent of high school seniors get drunk each month.
• Fewer than 5% of adults ride the bus to work in Los Angeles.
• The mean number of cars a person owns in her lifetime is not more than ten.
• About half of Americans prefer to live away from cities, given the choice.
• Europeans have a mean paid vacation each year of six weeks.
• The chance of developing breast cancer is under 11% for women.
• Private universities' mean tuition cost is more than $20,000 per year.
• \(H_{0}: \mu = 34; H_{a}: \mu \neq 34\)
• \(H_{0}: p \leq 0.60; H_{a}: p > 0.60\)
• \(H_{0}: \mu \geq 100,000; H_{a}: \mu < 100,000\)
• \(H_{0}: p = 0.29; H_{a}: p \neq 0.29\)
• \(H_{0}: p = 0.05; H_{a}: p < 0.05\)
• \(H_{0}: \mu \leq 10; H_{a}: \mu > 10\)
• \(H_{0}: p = 0.50; H_{a}: p \neq 0.50\)
• \(H_{0}: \mu = 6; H_{a}: \mu \neq 6\)
• \(H_{0}: p ≥ 0.11; H_{a}: p < 0.11\)
• \(H_{0}: \mu \leq 20,000; H_{a}: \mu > 20,000\)

Over the past few decades, public health officials have examined the link between weight concerns and teen girls' smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:

• \(p < 0.30\)
• \(p \leq 0.30\)
• \(p \geq 0.30\)
• \(p > 0.30\)

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:

• \(p = 0.20\)
• \(p > 0.20\)
• \(p < 0.20\)
• \(p \leq 0.20\)

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:

• \(H_{0}: \bar{x} = 4.5, H_{a}: \bar{x} > 4.5\)
• \(H_{0}: \mu \geq 4.5, H_{a}: \mu < 4.5\)
• \(H_{0}: \mu = 4.75, H_{a}: \mu > 4.75\)
• \(H_{0}: \mu = 4.5, H_{a}: \mu > 4.5\)

9.3: Outcomes and the Type I and Type II Errors

State the Type I and Type II errors in complete sentences given the following statements.

• The mean number of cars a person owns in his or her lifetime is not more than ten.
• Private universities mean tuition cost is more than $20,000 per year.
• Type I error: We conclude that the mean is not 34 years, when it really is 34 years. Type II error: We conclude that the mean is 34 years, when in fact it really is not 34 years.
• Type I error: We conclude that more than 60% of Americans vote in presidential elections, when the actual percentage is at most 60%.Type II error: We conclude that at most 60% of Americans vote in presidential elections when, in fact, more than 60% do.
• Type I error: We conclude that the mean starting salary is less than $100,000, when it really is at least $100,000. Type II error: We conclude that the mean starting salary is at least $100,000 when, in fact, it is less than $100,000.
• Type I error: We conclude that the proportion of high school seniors who get drunk each month is not 29%, when it really is 29%. Type II error: We conclude that the proportion of high school seniors who get drunk each month is 29% when, in fact, it is not 29%.
• Type I error: We conclude that fewer than 5% of adults ride the bus to work in Los Angeles, when the percentage that do is really 5% or more. Type II error: We conclude that 5% or more adults ride the bus to work in Los Angeles when, in fact, fewer that 5% do.
• Type I error: We conclude that the mean number of cars a person owns in his or her lifetime is more than 10, when in reality it is not more than 10. Type II error: We conclude that the mean number of cars a person owns in his or her lifetime is not more than 10 when, in fact, it is more than 10.
• Type I error: We conclude that the proportion of Americans who prefer to live away from cities is not about half, though the actual proportion is about half. Type II error: We conclude that the proportion of Americans who prefer to live away from cities is half when, in fact, it is not half.
• Type I error: We conclude that the duration of paid vacations each year for Europeans is not six weeks, when in fact it is six weeks. Type II error: We conclude that the duration of paid vacations each year for Europeans is six weeks when, in fact, it is not.
• Type I error: We conclude that the proportion is less than 11%, when it is really at least 11%. Type II error: We conclude that the proportion of women who develop breast cancer is at least 11%, when in fact it is less than 11%.
• Type I error: We conclude that the average tuition cost at private universities is more than $20,000, though in reality it is at most $20,000. Type II error: We conclude that the average tuition cost at private universities is at most $20,000 when, in fact, it is more than $20,000.

For statements a-j in Exercise 9.109 , answer the following in complete sentences.

• State a consequence of committing a Type I error.
• State a consequence of committing a Type II error.

When a new drug is created, the pharmaceutical company must subject it to testing before receiving the necessary permission from the Food and Drug Administration (FDA) to market the drug. Suppose the null hypothesis is “the drug is unsafe.” What is the Type II Error?

• To conclude the drug is safe when in, fact, it is unsafe.
• Not to conclude the drug is safe when, in fact, it is safe.
• To conclude the drug is safe when, in fact, it is safe.
• Not to conclude the drug is unsafe when, in fact, it is unsafe.

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 of them attended the midnight showing. The Type I error is to conclude that the percent of EVC students who attended is ________.

• at least 20%, when in fact, it is less than 20%.
• 20%, when in fact, it is 20%.
• less than 20%, when in fact, it is at least 20%.
• less than 20%, when in fact, it is less than 20%.

It is believed that Lake Tahoe Community College (LTCC) Intermediate Algebra students get less than seven hours of sleep per night, on average. A survey of 22 LTCC Intermediate Algebra students generated a mean of 7.24 hours with a standard deviation of 1.93 hours. At a level of significance of 5%, do LTCC Intermediate Algebra students get less than seven hours of sleep per night, on average?

The Type II error is not to reject that the mean number of hours of sleep LTCC students get per night is at least seven when, in fact, the mean number of hours

• is more than seven hours.
• is at most seven hours.
• is at least seven hours.
• is less than seven hours.

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test, the Type I error is:

• to conclude that the current mean hours per week is higher than 4.5, when in fact, it is higher
• to conclude that the current mean hours per week is higher than 4.5, when in fact, it is the same
• to conclude that the mean hours per week currently is 4.5, when in fact, it is higher
• to conclude that the mean hours per week currently is no higher than 4.5, when in fact, it is not higher

9.4: Distribution Needed for Hypothesis Testing

It is believed that Lake Tahoe Community College (LTCC) Intermediate Algebra students get less than seven hours of sleep per night, on average. A survey of 22 LTCC Intermediate Algebra students generated a mean of 7.24 hours with a standard deviation of 1.93 hours. At a level of significance of 5%, do LTCC Intermediate Algebra students get less than seven hours of sleep per night, on average? The distribution to be used for this test is \(\bar{X} \sim\) ________________

• \(N\left(7.24, \frac{1.93}{\sqrt{22}}\right)\)
• \(N\left(7.24, 1.93\right)\)

9.5: Rare Events, the Sample, Decision and Conclusion

The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. Conduct a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population.

• Is this a test of one mean or proportion?
• State the null and alternative hypotheses. \(H_{0}\) : ____________________ \(H_{a}\) : ____________________
• Is this a right-tailed, left-tailed, or two-tailed test?
• What symbol represents the random variable for this test?
• In words, define the random variable for this test.
• \(x =\) ________________
• \(n =\) ________________
• \(p′ =\) _____________
• Calculate \(\sigma_{x} =\) __________. Show the formula set-up.
• State the distribution to use for the hypothesis test.
• Find the \(p\text{-value}\).
• Reason for the decision:
• Conclusion (write out in a complete sentence):

9.6: Additional Information and Full Hypothesis Test Examples

For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in [link] . Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.

If you are using a Student's \(t\) - distribution for one of the following homework problems, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, however.)

A particular brand of tires claims that its deluxe tire averages at least 50,000 miles before it needs to be replaced. From past studies of this tire, the standard deviation is known to be 8,000. A survey of owners of that tire design is conducted. From the 28 tires surveyed, the mean lifespan was 46,500 miles with a standard deviation of 9,800 miles. Using \(\alpha = 0.05\), is the data highly inconsistent with the claim?

• \(H_{0}: \mu \geq 50,000\)
• \(H_{a}: \mu < 50,000\)
• Let \(\bar{X} =\) the average lifespan of a brand of tires.
• normal distribution
• \(z = -2.315\)
• \(p\text{-value} = 0.0103\)
• Check student’s solution.
• alpha: 0.05
• Decision: Reject the null hypothesis.
• Reason for decision: The \(p\text{-value}\) is less than 0.05.
• Conclusion: There is sufficient evidence to conclude that the mean lifespan of the tires is less than 50,000 miles.
• \((43,537, 49,463)\)

From generation to generation, the mean age when smokers first start to smoke varies. However, the standard deviation of that age remains constant of around 2.1 years. A survey of 40 smokers of this generation was done to see if the mean starting age is at least 19. The sample mean was 18.1 with a sample standard deviation of 1.3. Do the data support the claim at the 5% level?

The cost of a daily newspaper varies from city to city. However, the variation among prices remains steady with a standard deviation of 20¢. A study was done to test the claim that the mean cost of a daily newspaper is $1.00. Twelve costs yield a mean cost of 95¢ with a standard deviation of 18¢. Do the data support the claim at the 1% level?

• \(H_{0}: \mu = $1.00\)
• \(H_{a}: \mu \neq $1.00\)
• Let \(\bar{X} =\) the average cost of a daily newspaper.
• \(z = –0.866\)
• \(p\text{-value} = 0.3865\)
• \(\alpha: 0.01\)
• Decision: Do not reject the null hypothesis.
• Reason for decision: The \(p\text{-value}\) is greater than 0.01.
• Conclusion: There is sufficient evidence to support the claim that the mean cost of daily papers is $1. The mean cost could be $1.
• \(($0.84, $1.06)\)

An article in the San Jose Mercury News stated that students in the California state university system take 4.5 years, on average, to finish their undergraduate degrees. Suppose you believe that the mean time is longer. You conduct a survey of 49 students and obtain a sample mean of 5.1 with a sample standard deviation of 1.2. Do the data support your claim at the 1% level?

The mean number of sick days an employee takes per year is believed to be about ten. Members of a personnel department do not believe this figure. They randomly survey eight employees. The number of sick days they took for the past year are as follows: 12; 4; 15; 3; 11; 8; 6; 8. Let \(x =\) the number of sick days they took for the past year. Should the personnel team believe that the mean number is ten?

• \(H_{0}: \mu = 10\)
• \(H_{a}: \mu \neq 10\)
• Let \(\bar{X}\) the mean number of sick days an employee takes per year.
• Student’s t -distribution
• \(t = –1.12\)
• \(p\text{-value} = 0.300\)
• \(\alpha: 0.05\)
• Reason for decision: The \(p\text{-value}\) is greater than 0.05.
• Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the mean number of sick days is not ten.
• \((4.9443, 11.806)\)

In 1955, Life Magazine reported that the 25 year-old mother of three worked, on average, an 80 hour week. Recently, many groups have been studying whether or not the women's movement has, in fact, resulted in an increase in the average work week for women (combining employment and at-home work). Suppose a study was done to determine if the mean work week has increased. 81 women were surveyed with the following results. The sample mean was 83; the sample standard deviation was ten. Does it appear that the mean work week has increased for women at the 5% level?

Your statistics instructor claims that 60 percent of the students who take her Elementary Statistics class go through life feeling more enriched. For some reason that she can't quite figure out, most people don't believe her. You decide to check this out on your own. You randomly survey 64 of her past Elementary Statistics students and find that 34 feel more enriched as a result of her class. Now, what do you think?

• \(H_{0}: p \geq 0.6\)
• \(H_{a}: p < 0.6\)
• Let \(P′ =\) the proportion of students who feel more enriched as a result of taking Elementary Statistics.
• normal for a single proportion
• \(p\text{-value} = 0.1308\)
• Conclusion: There is insufficient evidence to conclude that less than 60 percent of her students feel more enriched.

The “plus-4s” confidence interval is \((0.411, 0.648)\)

A Nissan Motor Corporation advertisement read, “The average man’s I.Q. is 107. The average brown trout’s I.Q. is 4. So why can’t man catch brown trout?” Suppose you believe that the brown trout’s mean I.Q. is greater than four. You catch 12 brown trout. A fish psychologist determines the I.Q.s as follows: 5; 4; 7; 3; 6; 4; 5; 3; 6; 3; 8; 5. Conduct a hypothesis test of your belief.

Refer to Exercise 9.119 . Conduct a hypothesis test to see if your decision and conclusion would change if your belief were that the brown trout’s mean I.Q. is not four.

• \(H_{0}: \mu = 4\)
• \(H_{a}: \mu \neq 4\)
• Let \(\bar{X}\) the average I.Q. of a set of brown trout.
• two-tailed Student's t-test
• \(t = 1.95\)
• \(p\text{-value} = 0.076\)
• Reason for decision: The \(p\text{-value}\) is greater than 0.05
• Conclusion: There is insufficient evidence to conclude that the average IQ of brown trout is not four.
• \((3.8865,5.9468)\)

According to an article in Newsweek , the natural ratio of girls to boys is 100:105. In China, the birth ratio is 100: 114 (46.7% girls). Suppose you don’t believe the reported figures of the percent of girls born in China. You conduct a study. In this study, you count the number of girls and boys born in 150 randomly chosen recent births. There are 60 girls and 90 boys born of the 150. Based on your study, do you believe that the percent of girls born in China is 46.7?

A poll done for Newsweek found that 13% of Americans have seen or sensed the presence of an angel. A contingent doubts that the percent is really that high. It conducts its own survey. Out of 76 Americans surveyed, only two had seen or sensed the presence of an angel. As a result of the contingent’s survey, would you agree with the Newsweek poll? In complete sentences, also give three reasons why the two polls might give different results.

• \(H_{a}: p < 0.13\)
• Let \(P′ =\) the proportion of Americans who have seen or sensed angels
• –2.688
• \(p\text{-value} = 0.0036\)
• Reason for decision: The \(p\text{-value}\)e is less than 0.05.
• Conclusion: There is sufficient evidence to conclude that the percentage of Americans who have seen or sensed an angel is less than 13%.

The“plus-4s” confidence interval is (0.0022, 0.0978)

The mean work week for engineers in a start-up company is believed to be about 60 hours. A newly hired engineer hopes that it’s shorter. She asks ten engineering friends in start-ups for the lengths of their mean work weeks. Based on the results that follow, should she count on the mean work week to be shorter than 60 hours?

Data (length of mean work week): 70; 45; 55; 60; 65; 55; 55; 60; 50; 55.

Use the “Lap time” data for Lap 4 (see [link] ) to test the claim that Terri finishes Lap 4, on average, in less than 129 seconds. Use all twenty races given.

• \(H_{0}: \mu \geq 129\)
• \(H_{a}: \mu < 129\)
• Let \(\bar{X} =\) the average time in seconds that Terri finishes Lap 4.
• Student's t -distribution
• \(t = 1.209\)
• Conclusion: There is insufficient evidence to conclude that Terri’s mean lap time is less than 129 seconds.
• \((128.63, 130.37)\)

Use the “Initial Public Offering” data (see [link] ) to test the claim that the mean offer price was $18 per share. Do not use all the data. Use your random number generator to randomly survey 15 prices.

The following questions were written by past students. They are excellent problems!

"Asian Family Reunion," by Chau Nguyen

Every two years it comes around.

We all get together from different towns.

In my honest opinion,

It's not a typical family reunion.

Not forty, or fifty, or sixty,

But how about seventy companions!

The kids would play, scream, and shout

One minute they're happy, another they'll pout.

The teenagers would look, stare, and compare

From how they look to what they wear.

The men would chat about their business

That they make more, but never less.

Money is always their subject

And there's always talk of more new projects.

The women get tired from all of the chats

They head to the kitchen to set out the mats.

Some would sit and some would stand

Eating and talking with plates in their hands.

Then come the games and the songs

And suddenly, everyone gets along!

With all that laughter, it's sad to say

That it always ends in the same old way.

They hug and kiss and say "good-bye"

And then they all begin to cry!

I say that 60 percent shed their tears

But my mom counted 35 people this year.

She said that boys and men will always have their pride,

So we won't ever see them cry.

I myself don't think she's correct,

So could you please try this problem to see if you object?

• \(H_{0}: p = 0.60\)
• \(H_{a}: p < 0.60\)
• Let \(P′ =\) the proportion of family members who shed tears at a reunion.
• –1.71
• Reason for decision: \(p\text{-value} < \alpha\)
• Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the proportion of family members who shed tears at a reunion is less than 0.60. However, the test is weak because the \(p\text{-value}\) and alpha are quite close, so other tests should be done.
• We are 95% confident that between 38.29% and 61.71% of family members will shed tears at a family reunion. \((0.3829, 0.6171)\). The“plus-4s” confidence interval (see chapter 8) is \((0.3861, 0.6139)\)

Note that here the “large-sample” \(1 - \text{PropZTest}\) provides the approximate \(p\text{-value}\) of 0.0438. Whenever a \(p\text{-value}\) based on a normal approximation is close to the level of significance, the exact \(p\text{-value}\) based on binomial probabilities should be calculated whenever possible. This is beyond the scope of this course.

"The Problem with Angels," by Cyndy Dowling

Although this problem is wholly mine,

The catalyst came from the magazine, Time.

On the magazine cover I did find

The realm of angels tickling my mind.

Inside, 69% I found to be

In angels, Americans do believe.

Then, it was time to rise to the task,

Ninety-five high school and college students I did ask.

Viewing all as one group,

Random sampling to get the scoop.

So, I asked each to be true,

"Do you believe in angels?" Tell me, do!

Hypothesizing at the start,

Totally believing in my heart

That the proportion who said yes

Would be equal on this test.

Lo and behold, seventy-three did arrive,

Out of the sample of ninety-five.

Now your job has just begun,

Solve this problem and have some fun.

"Blowing Bubbles," by Sondra Prull

Studying stats just made me tense,

I had to find some sane defense.

Some light and lifting simple play

To float my math anxiety away.

Blowing bubbles lifts me high

Takes my troubles to the sky.

POIK! They're gone, with all my stress

Bubble therapy is the best.

The label said each time I blew

The average number of bubbles would be at least 22.

I blew and blew and this I found

From 64 blows, they all are round!

But the number of bubbles in 64 blows

Varied widely, this I know.

20 per blow became the mean

They deviated by 6, and not 16.

From counting bubbles, I sure did relax

But now I give to you your task.

Was 22 a reasonable guess?

Find the answer and pass this test!

• \(H_{0}: \mu \geq 22\)
• \(H_{a}: \mu < 22\)
• Let \(\bar{X} =\) the mean number of bubbles per blow.
• –2.667
• \(p\text{-value} = 0.00486\)
• Conclusion: There is sufficient evidence to conclude that the mean number of bubbles per blow is less than 22.
• \((18.501, 21.499)\)

"Dalmatian Darnation," by Kathy Sparling

A greedy dog breeder named Spreckles

Bred puppies with numerous freckles

The Dalmatians he sought

Possessed spot upon spot

The more spots, he thought, the more shekels.

His competitors did not agree

That freckles would increase the fee.

They said, “Spots are quite nice

But they don't affect price;

One should breed for improved pedigree.”

The breeders decided to prove

This strategy was a wrong move.

Breeding only for spots

Would wreak havoc, they thought.

His theory they want to disprove.

They proposed a contest to Spreckles

Comparing dog prices to freckles.

In records they looked up

One hundred one pups:

Dalmatians that fetched the most shekels.

They asked Mr. Spreckles to name

An average spot count he'd claim

To bring in big bucks.

Said Spreckles, “Well, shucks,

It's for one hundred one that I aim.”

Said an amateur statistician

Who wanted to help with this mission.

“Twenty-one for the sample

Standard deviation's ample:

They examined one hundred and one

Dalmatians that fetched a good sum.

They counted each spot,

Mark, freckle and dot

And tallied up every one.

Instead of one hundred one spots

They averaged ninety six dots

Can they muzzle Spreckles’

Obsession with freckles

Based on all the dog data they've got?

"Macaroni and Cheese, please!!" by Nedda Misherghi and Rachelle Hall

As a poor starving student I don't have much money to spend for even the bare necessities. So my favorite and main staple food is macaroni and cheese. It's high in taste and low in cost and nutritional value.

One day, as I sat down to determine the meaning of life, I got a serious craving for this, oh, so important, food of my life. So I went down the street to Greatway to get a box of macaroni and cheese, but it was SO expensive! $2.02 !!! Can you believe it? It made me stop and think. The world is changing fast. I had thought that the mean cost of a box (the normal size, not some super-gigantic-family-value-pack) was at most $1, but now I wasn't so sure. However, I was determined to find out. I went to 53 of the closest grocery stores and surveyed the prices of macaroni and cheese. Here are the data I wrote in my notebook:

Price per box of Mac and Cheese:

• 5 stores @ $2.02
• 15 stores @ $0.25
• 3 stores @ $1.29
• 6 stores @ $0.35
• 4 stores @ $2.27
• 7 stores @ $1.50
• 5 stores @ $1.89
• 8 stores @ 0.75.

I could see that the cost varied but I had to sit down to figure out whether or not I was right. If it does turn out that this mouth-watering dish is at most $1, then I'll throw a big cheesy party in our next statistics lab, with enough macaroni and cheese for just me. (After all, as a poor starving student I can't be expected to feed our class of animals!)

• \(H_{0}: \mu \leq 1\)
• \(H_{a}: \mu > 1\)
• Let \(\bar{X} =\) the mean cost in dollars of macaroni and cheese in a certain town.
• Student's \(t\)-distribution
• \(t = 0.340\)
• \(p\text{-value} = 0.36756\)
• Conclusion: The mean cost could be $1, or less. At the 5% significance level, there is insufficient evidence to conclude that the mean price of a box of macaroni and cheese is more than $1.
• \((0.8291, 1.241)\)

"William Shakespeare: The Tragedy of Hamlet, Prince of Denmark," by Jacqueline Ghodsi

THE CHARACTERS (in order of appearance):

• HAMLET, Prince of Denmark and student of Statistics
• POLONIUS, Hamlet’s tutor
• HOROTIO, friend to Hamlet and fellow student

Scene: The great library of the castle, in which Hamlet does his lessons

(The day is fair, but the face of Hamlet is clouded. He paces the large room. His tutor, Polonius, is reprimanding Hamlet regarding the latter’s recent experience. Horatio is seated at the large table at right stage.)

POLONIUS: My Lord, how cans’t thou admit that thou hast seen a ghost! It is but a figment of your imagination!

HAMLET: I beg to differ; I know of a certainty that five-and-seventy in one hundred of us, condemned to the whips and scorns of time as we are, have gazed upon a spirit of health, or goblin damn’d, be their intents wicked or charitable.

POLONIUS If thou doest insist upon thy wretched vision then let me invest your time; be true to thy work and speak to me through the reason of the null and alternate hypotheses. (He turns to Horatio.) Did not Hamlet himself say, “What piece of work is man, how noble in reason, how infinite in faculties? Then let not this foolishness persist. Go, Horatio, make a survey of three-and-sixty and discover what the true proportion be. For my part, I will never succumb to this fantasy, but deem man to be devoid of all reason should thy proposal of at least five-and-seventy in one hundred hold true.

HORATIO (to Hamlet): What should we do, my Lord?

HAMLET: Go to thy purpose, Horatio.

HORATIO: To what end, my Lord?

HAMLET: That you must teach me. But let me conjure you by the rights of our fellowship, by the consonance of our youth, but the obligation of our ever-preserved love, be even and direct with me, whether I am right or no.

(Horatio exits, followed by Polonius, leaving Hamlet to ponder alone.)

(The next day, Hamlet awaits anxiously the presence of his friend, Horatio. Polonius enters and places some books upon the table just a moment before Horatio enters.)

POLONIUS: So, Horatio, what is it thou didst reveal through thy deliberations?

HORATIO: In a random survey, for which purpose thou thyself sent me forth, I did discover that one-and-forty believe fervently that the spirits of the dead walk with us. Before my God, I might not this believe, without the sensible and true avouch of mine own eyes.

POLONIUS: Give thine own thoughts no tongue, Horatio. (Polonius turns to Hamlet.) But look to’t I charge you, my Lord. Come Horatio, let us go together, for this is not our test. (Horatio and Polonius leave together.)

HAMLET: To reject, or not reject, that is the question: whether ‘tis nobler in the mind to suffer the slings and arrows of outrageous statistics, or to take arms against a sea of data, and, by opposing, end them. (Hamlet resignedly attends to his task.)

(Curtain falls)

"Untitled," by Stephen Chen

I've often wondered how software is released and sold to the public. Ironically, I work for a company that sells products with known problems. Unfortunately, most of the problems are difficult to create, which makes them difficult to fix. I usually use the test program X, which tests the product, to try to create a specific problem. When the test program is run to make an error occur, the likelihood of generating an error is 1%.

So, armed with this knowledge, I wrote a new test program Y that will generate the same error that test program X creates, but more often. To find out if my test program is better than the original, so that I can convince the management that I'm right, I ran my test program to find out how often I can generate the same error. When I ran my test program 50 times, I generated the error twice. While this may not seem much better, I think that I can convince the management to use my test program instead of the original test program. Am I right?

• \(H_{0}: p = 0.01\)
• \(H_{a}: p > 0.01\)
• Let \(P′ =\) the proportion of errors generated
• Normal for a single proportion
• Decision: Reject the null hypothesis
• Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the proportion of errors generated is more than 0.01.

The“plus-4s” confidence interval is \((0.004, 0.144)\).

"Japanese Girls’ Names"

by Kumi Furuichi

It used to be very typical for Japanese girls’ names to end with “ko.” (The trend might have started around my grandmothers’ generation and its peak might have been around my mother’s generation.) “Ko” means “child” in Chinese characters. Parents would name their daughters with “ko” attaching to other Chinese characters which have meanings that they want their daughters to become, such as Sachiko—happy child, Yoshiko—a good child, Yasuko—a healthy child, and so on.

However, I noticed recently that only two out of nine of my Japanese girlfriends at this school have names which end with “ko.” More and more, parents seem to have become creative, modernized, and, sometimes, westernized in naming their children.

I have a feeling that, while 70 percent or more of my mother’s generation would have names with “ko” at the end, the proportion has dropped among my peers. I wrote down all my Japanese friends’, ex-classmates’, co-workers, and acquaintances’ names that I could remember. Following are the names. (Some are repeats.) Test to see if the proportion has dropped for this generation.

Ai, Akemi, Akiko, Ayumi, Chiaki, Chie, Eiko, Eri, Eriko, Fumiko, Harumi, Hitomi, Hiroko, Hiroko, Hidemi, Hisako, Hinako, Izumi, Izumi, Junko, Junko, Kana, Kanako, Kanayo, Kayo, Kayoko, Kazumi, Keiko, Keiko, Kei, Kumi, Kumiko, Kyoko, Kyoko, Madoka, Maho, Mai, Maiko, Maki, Miki, Miki, Mikiko, Mina, Minako, Miyako, Momoko, Nana, Naoko, Naoko, Naoko, Noriko, Rieko, Rika, Rika, Rumiko, Rei, Reiko, Reiko, Sachiko, Sachiko, Sachiyo, Saki, Sayaka, Sayoko, Sayuri, Seiko, Shiho, Shizuka, Sumiko, Takako, Takako, Tomoe, Tomoe, Tomoko, Touko, Yasuko, Yasuko, Yasuyo, Yoko, Yoko, Yoko, Yoshiko, Yoshiko, Yoshiko, Yuka, Yuki, Yuki, Yukiko, Yuko, Yuko.

"Phillip’s Wish," by Suzanne Osorio

My nephew likes to play

Chasing the girls makes his day.

He asked his mother

If it is okay

To get his ear pierced.

She said, “No way!”

To poke a hole through your ear,

Is not what I want for you, dear.

He argued his point quite well,

Says even my macho pal, Mel,

Has gotten this done.

It’s all just for fun.

C’mon please, mom, please, what the hell.

Again Phillip complained to his mother,

Saying half his friends (including their brothers)

Are piercing their ears

And they have no fears

He wants to be like the others.

She said, “I think it’s much less.

We must do a hypothesis test.

And if you are right,

I won’t put up a fight.

But, if not, then my case will rest.”

We proceeded to call fifty guys

To see whose prediction would fly.

Nineteen of the fifty

Said piercing was nifty

And earrings they’d occasionally buy.

Then there’s the other thirty-one,

Who said they’d never have this done.

So now this poem’s finished.

Will his hopes be diminished,

Or will my nephew have his fun?

• \(H_{0}: p = 0.50\)
• \(H_{a}: p < 0.50\)
• Let \(P′ =\) the proportion of friends that has a pierced ear.
• –1.70
• \(p\text{-value} = 0.0448\)
• Reason for decision: The \(p\text{-value}\) is less than 0.05. (However, they are very close.)
• Conclusion: There is sufficient evidence to support the claim that less than 50% of his friends have pierced ears.
• Confidence Interval: \((0.245, 0.515)\): The “plus-4s” confidence interval is \((0.259, 0.519)\).

"The Craven," by Mark Salangsang

Once upon a morning dreary

In stats class I was weak and weary.

Pondering over last night’s homework

Whose answers were now on the board

This I did and nothing more.

While I nodded nearly napping

Suddenly, there came a tapping.

As someone gently rapping,

Rapping my head as I snore.

Quoth the teacher, “Sleep no more.”

“In every class you fall asleep,”

The teacher said, his voice was deep.

“So a tally I’ve begun to keep

Of every class you nap and snore.

The percentage being forty-four.”

“My dear teacher I must confess,

While sleeping is what I do best.

The percentage, I think, must be less,

A percentage less than forty-four.”

This I said and nothing more.

“We’ll see,” he said and walked away,

And fifty classes from that day

He counted till the month of May

The classes in which I napped and snored.

The number he found was twenty-four.

At a significance level of 0.05,

Please tell me am I still alive?

Or did my grade just take a dive

Plunging down beneath the floor?

Upon thee I hereby implore.

Toastmasters International cites a report by Gallop Poll that 40% of Americans fear public speaking. A student believes that less than 40% of students at her school fear public speaking. She randomly surveys 361 schoolmates and finds that 135 report they fear public speaking. Conduct a hypothesis test to determine if the percent at her school is less than 40%.

• \(H_{0}: p = 0.40\)
• \(H_{a}: p < 0.40\)
• Let \(P′ =\) the proportion of schoolmates who fear public speaking.
• –1.01
• \(p\text{-value} = 0.1563\)
• Conclusion: There is insufficient evidence to support the claim that less than 40% of students at the school fear public speaking.
• Confidence Interval: \((0.3241, 0.4240)\): The “plus-4s” confidence interval is \((0.3257, 0.4250)\).

Sixty-eight percent of online courses taught at community colleges nationwide were taught by full-time faculty. To test if 68% also represents California’s percent for full-time faculty teaching the online classes, Long Beach City College (LBCC) in California, was randomly selected for comparison. In the same year, 34 of the 44 online courses LBCC offered were taught by full-time faculty. Conduct a hypothesis test to determine if 68% represents California. NOTE: For more accurate results, use more California community colleges and this past year's data.

According to an article in Bloomberg Businessweek , New York City's most recent adult smoking rate is 14%. Suppose that a survey is conducted to determine this year’s rate. Nine out of 70 randomly chosen N.Y. City residents reply that they smoke. Conduct a hypothesis test to determine if the rate is still 14% or if it has decreased.

• \(H_{0}: p = 0.14\)
• \(H_{a}: p < 0.14\)
• Let \(P′ =\) the proportion of NYC residents that smoke.
• –0.2756
• \(p\text{-value} = 0.3914\)
• At the 5% significance level, there is insufficient evidence to conclude that the proportion of NYC residents who smoke is less than 0.14.
• Confidence Interval: \((0.0502, 0.2070)\): The “plus-4s” confidence interval (see chapter 8) is \((0.0676, 0.2297)\).

The mean age of De Anza College students in a previous term was 26.6 years old. An instructor thinks the mean age for online students is older than 26.6. She randomly surveys 56 online students and finds that the sample mean is 29.4 with a standard deviation of 2.1. Conduct a hypothesis test.

Registered nurses earned an average annual salary of $69,110. For that same year, a survey was conducted of 41 California registered nurses to determine if the annual salary is higher than $69,110 for California nurses. The sample average was $71,121 with a sample standard deviation of $7,489. Conduct a hypothesis test.

• \(H_{0}: \mu = 69,110\)
• \(H_{0}: \mu > 69,110\)
• Let \(\bar{X} =\) the mean salary in dollars for California registered nurses.
• \(t = 1.719\)
• \(p\text{-value}: 0.0466\)
• Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean salary of California registered nurses exceeds $69,110.
• \(($68,757, $73,485)\)

La Leche League International reports that the mean age of weaning a child from breastfeeding is age four to five worldwide. In America, most nursing mothers wean their children much earlier. Suppose a random survey is conducted of 21 U.S. mothers who recently weaned their children. The mean weaning age was nine months (3/4 year) with a standard deviation of 4 months. Conduct a hypothesis test to determine if the mean weaning age in the U.S. is less than four years old.

Over the past few decades, public health officials have examined the link between weight concerns and teen girls' smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin?

After conducting the test, your decision and conclusion are

• Reject \(H_{0}\): There is sufficient evidence to conclude that more than 30% of teen girls smoke to stay thin.
• Do not reject \(H_{0}\): There is not sufficient evidence to conclude that less than 30% of teen girls smoke to stay thin.
• Do not reject \(H_{0}\): There is not sufficient evidence to conclude that more than 30% of teen girls smoke to stay thin.
• Reject \(H_{0}\): There is sufficient evidence to conclude that less than 30% of teen girls smoke to stay thin.

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 of them attended the midnight showing.

At a 1% level of significance, an appropriate conclusion is:

• There is insufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is less than 20%.
• There is sufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is more than 20%.
• There is sufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is less than 20%.
• There is insufficient evidence to conclude that the percent of EVC students who attended the midnight showing of Harry Potter is at least 20%.

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test.

At a significance level of \(a = 0.05\), what is the correct conclusion?

• There is enough evidence to conclude that the mean number of hours is more than 4.75
• There is enough evidence to conclude that the mean number of hours is more than 4.5
• There is not enough evidence to conclude that the mean number of hours is more than 4.5
• There is not enough evidence to conclude that the mean number of hours is more than 4.75

Instructions: For the following ten exercises,

Hypothesis testing: For the following ten exercises, answer each question.

State the null and alternate hypothesis.

State the \(p\text{-value}\).

State \(\alpha\).

What is your decision?

Write a conclusion.

Answer any other questions asked in the problem.

According to the Center for Disease Control website, in 2011 at least 18% of high school students have smoked a cigarette. An Introduction to Statistics class in Davies County, KY conducted a hypothesis test at the local high school (a medium sized–approximately 1,200 students–small city demographic) to determine if the local high school’s percentage was lower. One hundred fifty students were chosen at random and surveyed. Of the 150 students surveyed, 82 have smoked. Use a significance level of 0.05 and using appropriate statistical evidence, conduct a hypothesis test and state the conclusions.

A recent survey in the N.Y. Times Almanac indicated that 48.8% of families own stock. A broker wanted to determine if this survey could be valid. He surveyed a random sample of 250 families and found that 142 owned some type of stock. At the 0.05 significance level, can the survey be considered to be accurate?

• \(H_{0}: p = 0.488\) \(H_{a}: p \neq 0.488\)
• \(p\text{-value} = 0.0114\)
• \(\alpha = 0.05\)
• Reject the null hypothesis.
• At the 5% level of significance, there is enough evidence to conclude that 48.8% of families own stocks.
• The survey does not appear to be accurate.

Driver error can be listed as the cause of approximately 54% of all fatal auto accidents, according to the American Automobile Association. Thirty randomly selected fatal accidents are examined, and it is determined that 14 were caused by driver error. Using \(\alpha = 0.05\), is the AAA proportion accurate?

The US Department of Energy reported that 51.7% of homes were heated by natural gas. A random sample of 221 homes in Kentucky found that 115 were heated by natural gas. Does the evidence support the claim for Kentucky at the \(\alpha = 0.05\) level in Kentucky? Are the results applicable across the country? Why?

• \(H_{0}: p = 0.517\) \(H_{0}: p \neq 0.517\)
• \(p\text{-value} = 0.9203\).
• \(\alpha = 0.05\).
• Do not reject the null hypothesis.
• At the 5% significance level, there is not enough evidence to conclude that the proportion of homes in Kentucky that are heated by natural gas is 0.517.
• However, we cannot generalize this result to the entire nation. First, the sample’s population is only the state of Kentucky. Second, it is reasonable to assume that homes in the extreme north and south will have extreme high usage and low usage, respectively. We would need to expand our sample base to include these possibilities if we wanted to generalize this claim to the entire nation.

For Americans using library services, the American Library Association claims that at most 67% of patrons borrow books. The library director in Owensboro, Kentucky feels this is not true, so she asked a local college statistic class to conduct a survey. The class randomly selected 100 patrons and found that 82 borrowed books. Did the class demonstrate that the percentage was higher in Owensboro, KY? Use \(\alpha = 0.01\) level of significance. What is the possible proportion of patrons that do borrow books from the Owensboro Library?

The Weather Underground reported that the mean amount of summer rainfall for the northeastern US is at least 11.52 inches. Ten cities in the northeast are randomly selected and the mean rainfall amount is calculated to be 7.42 inches with a standard deviation of 1.3 inches. At the \(\alpha = 0.05 level\), can it be concluded that the mean rainfall was below the reported average? What if \(\alpha = 0.01\)? Assume the amount of summer rainfall follows a normal distribution.

• \(H_{0}: \mu \geq 11.52\) \(H_{a}: \mu < 11.52\)
• \(p\text{-value} = 0.000002\) which is almost 0.
• At the 5% significance level, there is enough evidence to conclude that the mean amount of summer rain in the northeaster US is less than 11.52 inches, on average.
• We would make the same conclusion if alpha was 1% because the \(p\text{-value}\) is almost 0.

A survey in the N.Y. Times Almanac finds the mean commute time (one way) is 25.4 minutes for the 15 largest US cities. The Austin, TX chamber of commerce feels that Austin’s commute time is less and wants to publicize this fact. The mean for 25 randomly selected commuters is 22.1 minutes with a standard deviation of 5.3 minutes. At the \(\alpha = 0.10\) level, is the Austin, TX commute significantly less than the mean commute time for the 15 largest US cities?

A report by the Gallup Poll found that a woman visits her doctor, on average, at most 5.8 times each year. A random sample of 20 women results in these yearly visit totals

3; 2; 1; 3; 7; 2; 9; 4; 6; 6; 8; 0; 5; 6; 4; 2; 1; 3; 4; 1

At the \(\alpha = 0.05\) level can it be concluded that the sample mean is higher than 5.8 visits per year?

• \(H_{0}: \mu \leq 5.8\) \(H_{a}: \mu > 5.8\)
• \(p\text{-value} = 0.9987\)
• At the 5% level of significance, there is not enough evidence to conclude that a woman visits her doctor, on average, more than 5.8 times a year.

According to the N.Y. Times Almanac the mean family size in the U.S. is 3.18. A sample of a college math class resulted in the following family sizes:

5; 4; 5; 4; 4; 3; 6; 4; 3; 3; 5; 5; 6; 3; 3; 2; 7; 4; 5; 2; 2; 2; 3; 2

At \(\alpha = 0.05\) level, is the class’ mean family size greater than the national average? Does the Almanac result remain valid? Why?

The student academic group on a college campus claims that freshman students study at least 2.5 hours per day, on average. One Introduction to Statistics class was skeptical. The class took a random sample of 30 freshman students and found a mean study time of 137 minutes with a standard deviation of 45 minutes. At α = 0.01 level, is the student academic group’s claim correct?

• \(H_{0}: \mu \geq 150\) \(H_{0}: \mu < 150\)
• \(p\text{-value} = 0.0622\)
• \(\alpha = 0.01\)
• At the 1% significance level, there is not enough evidence to conclude that freshmen students study less than 2.5 hours per day, on average.
• The student academic group’s claim appears to be correct.

9.7: Hypothesis Testing of a Single Mean and Single Proportion

• Data Science

Hypothesis Testing in Data Science [Types, Process, Example]

Home Blog Data Science Hypothesis Testing in Data Science [Types, Process, Example]

In day-to-day life, we come across a lot of data lot of variety of content. Sometimes the information is too much that we get confused about whether the information provided is correct or not. At that moment, we get introduced to a word called “Hypothesis testing” which helps in determining the proofs and pieces of evidence for some belief or information.  

What is Hypothesis Testing?

Hypothesis testing is an integral part of statistical inference. It is used to decide whether the given sample data from the population parameter satisfies the given hypothetical condition. So, it will predict and decide using several factors whether the predictions satisfy the conditions or not. In simpler terms, trying to prove whether the facts or statements are true or not.   

For example, if you predict that students who sit on the last bench are poorer and weaker than students sitting on 1st bench, then this is a hypothetical statement that needs to be clarified using different experiments. Another example we can see is implementing new business strategies to evaluate whether they will work for the business or not. All these things are very necessary when you work with data as a data scientist.  If you are interested in learning about data science, visit this amazing  Data Science full course   to learn data science.    

How is Hypothesis Testing Used in Data Science?

It is important to know how and where we can use hypothesis testing techniques in the field of data science. Data scientists predict a lot of things in their day-to-day work, and to check the probability of whether that finding is certain or not, we use hypothesis testing. The main goal of hypothesis testing is to gauge how well the predictions perform based on the sample data provided by the population. If you are interested to know more about the applications of the data, then refer to this  D ata  Scien ce course in India  which will give you more insights into application-based things. When data scientists work on model building using various machine learning algorithms, they need to have faith in their models and the forecasting of models. They then provide the sample data to the model for training purposes so that it can provide us with the significance of statistical data that will represent the entire population.  

Where and When to Use Hypothesis Test?

Hypothesis testing is widely used when we need to compare our results based on predictions. So, it will compare before and after results. For example, someone claimed that students writing exams from blue pen always get above 90%; now this statement proves it correct, and experiments need to be done. So, the data will be collected based on the student's input, and then the test will be done on the final result later after various experiments and observations on students' marks vs pen used, final conclusions will be made which will determine the results. Now hypothesis testing will be done to compare the 1st and the 2nd result, to see the difference and closeness of both outputs. This is how hypothesis testing is done.  

How Does Hypothesis Testing Work in Data Science?

In the whole data science life cycle, hypothesis testing is done in various stages, starting from the initial part, the 1st stage where the EDA, data pre-processing, and manipulation are done. In this stage, we will do our initial hypothesis testing to visualize the outcome in later stages. The next test will be done after we have built our model, once the model is ready and hypothesis testing is done, we will compare the results of the initial testing and the 2nd one to compare the results and significance of the results and to confirm the insights generated from the 1st cycle match with the 2nd one or not. This will help us know how the model responds to the sample training data. As we saw above, hypothesis testing is always needed when we are planning to contrast more than 2 groups. While checking on the results, it is important to check on the flexibility of the results for the sample and the population. Later, we can judge on the disagreement of the results are appropriate or vague. This is all we can do using hypothesis testing.   

Different Types of Hypothesis Testing

Hypothesis testing can be seen in several types. In total, we have 5 types of hypothesis testing. They are described below:

1. Alternative Hypothesis

The alternative hypothesis explains and defines the relationship between two variables. It simply indicates a positive relationship between two variables which means they do have a statistical bond. It indicates that the sample observed is going to influence or affect the outcome. An alternative hypothesis is described using H a  or H 1 . Ha indicates an alternative hypothesis and H 1  explains the possibility of influenced outcome which is 1. For example, children who study from the beginning of the class have fewer chances to fail. An alternate hypothesis will be accepted once the statistical predictions become significant. The alternative hypothesis can be further divided into 3 parts.   

• Left-tailed: Left tailed hypothesis can be expected when the sample value is less than the true value.   
• Right-tailed: Right-tailed hypothesis can be expected when the true value is greater than the outcome/predicted value.    
• Two-tailed: Two-tailed hypothesis is defined when the true value is not equal to the sample value or the output.   

2. Null Hypothesis

The null hypothesis simply states that there is no relation between statistical variables. If the facts presented at the start do not match with the outcomes, then we can say, the testing is null hypothesis testing. The null hypothesis is represented as H 0 . For example, children who study from the beginning of the class have no fewer chances to fail. There are types of Null Hypothesis described below:   

Simple Hypothesis:  It helps in denoting and indicating the distribution of the population.   

Composite Hypothesis:  It does not denote the population distribution   

Exact Hypothesis:  In the exact hypothesis, the value of the hypothesis is the same as the sample distribution. Example- μ= 10   

Inexact Hypothesis:  Here, the hypothesis values are not equal to the sample. It will denote a particular range of values.   

3. Non-directional Hypothesis 

The non-directional hypothesis is a tow-tailed hypothesis that indicates the true value does not equal the predicted value. In simpler terms, there is no direction between the 2 variables. For an example of a non-directional hypothesis, girls and boys have different methodologies to solve a problem. Here the example explains that the thinking methodologies of a girl and a boy is different, they don’t think alike.    

4. Directional Hypothesis

In the Directional hypothesis, there is a direct relationship between two variables. Here any of the variables influence the other.   

5. Statistical Hypothesis

Statistical hypothesis helps in understanding the nature and character of the population. It is a great method to decide whether the values and the data we have with us satisfy the given hypothesis or not. It helps us in making different probabilistic and certain statements to predict the outcome of the population... We have several types of tests which are the T-test, Z-test, and Anova tests.  

Methods of Hypothesis Testing

1. frequentist hypothesis testing.

Frequentist hypotheses mostly work with the approach of making predictions and assumptions based on the current data which is real-time data. All the facts are based on current data. The most famous kind of frequentist approach is null hypothesis testing.    

2. Bayesian Hypothesis Testing

Bayesian testing is a modern and latest way of hypothesis testing. It is known to be the test that works with past data to predict the future possibilities of the hypothesis. In Bayesian, it refers to the prior distribution or prior probability samples for the observed data. In the medical Industry, we observe that Doctors deal with patients’ diseases using past historical records. So, with this kind of record, it is helpful for them to understand and predict the current and upcoming health conditions of the patient.

Importance of Hypothesis Testing in Data Science

Most of the time, people assume that data science is all about applying machine learning algorithms and getting results, that is true but in addition to the fact that to work in the data science field, one needs to be well versed with statistics as most of the background work in Data science is done through statistics. When we deal with data for pre-processing, manipulating, and analyzing, statistics play. Specifically speaking Hypothesis testing helps in making confident decisions, predicting the correct outcomes, and finding insightful conclusions regarding the population. Hypothesis testing helps us resolve tough things easily. To get more familiar with Hypothesis testing and other prediction models attend the superb useful  KnowledgeHut Data Science full course  which will give you more domain knowledge and will assist you in working with industry-related projects.          

Basic Steps in Hypothesis Testing [Workflow]

1. null and alternative hypothesis.

After we have done our initial research about the predictions that we want to find out if true, it is important to mention whether the hypothesis done is a null hypothesis(H0) or an alternative hypothesis (Ha). Once we understand the type of hypothesis, it will be easy for us to do mathematical research on it. A null hypothesis will usually indicate the no-relationship between the variables whereas an alternative hypothesis describes the relationship between 2 variables.    

• H0 – Girls, on average, are not strong as boys   
• Ha - Girls, on average are stronger than boys   

2. Data Collection

To prove our statistical test validity, it is essential and critical to check the data and proceed with sampling them to get the correct hypothesis results. If the target data is not prepared and ready, it will become difficult to make the predictions or the statistical inference on the population that we are planning to make. It is important to prepare efficient data, so that hypothesis findings can be easy to predict.   

3. Selection of an appropriate test statistic

To perform various analyses on the data, we need to choose a statistical test. There are various types of statistical tests available. Based on the wide spread of the data that is variance within the group or how different the data category is from one another that is variance without a group, we can proceed with our further research study.   

4. Selection of the appropriate significant level

Once we get the result and outcome of the statistical test, we have to then proceed further to decide whether the reject or accept the null hypothesis. The significance level is indicated by alpha (α). It describes the probability of rejecting or accepting the null hypothesis. Example- Suppose the value of the significance level which is alpha is 0.05. Now, this value indicates the difference from the null hypothesis. 

5. Calculation of the test statistics and the p-value

P value is simply the probability value and expected determined outcome which is at least as extreme and close as observed results of a hypothetical test. It helps in evaluating and verifying hypotheses against the sample data. This happens while assuming the null hypothesis is true. The lower the value of P, the higher and better will be the results of the significant value which is alpha (α). For example, if the P-value is 0.05 or even less than this, then it will be considered statistically significant. The main thing is these values are predicted based on the calculations done by deviating the values between the observed one and referenced one. The greater the difference between values, the lower the p-value will be.

6. Findings of the test

After knowing the P-value and statistical significance, we can determine our results and take the appropriate decision of whether to accept or reject the null hypothesis based on the facts and statistics presented to us.

How to Calculate Hypothesis Testing?

Hypothesis testing can be done using various statistical tests. One is Z-test. The formula for Z-test is given below:  

            Z = ( x̅  – μ 0 )  / (σ /√n)    

In the above equation, x̅ is the sample mean   

• μ0 is the population mean   
• σ is the standard deviation    
• n is the sample size   

Now depending on the Z-test result, the examination will be processed further. The result is either going to be a null hypothesis or it is going to be an alternative hypothesis. That can be measured through below formula-   

• H0: μ=μ0   
• Ha: μ≠μ0   
• Here,   
• H0 = null hypothesis   
• Ha = alternate hypothesis   

In this way, we calculate the hypothesis testing and can apply it to real-world scenarios.

Real-World Examples of Hypothesis Testing

Hypothesis testing has a wide variety of use cases that proves to be beneficial for various industries.    

1. Healthcare

In the healthcare industry, all the research and experiments which are done to predict the success of any medicine or drug are done successfully with the help of Hypothesis testing.   

2. Education sector

Hypothesis testing assists in experimenting with different teaching techniques to deal with the understanding capability of different students.   

3. Mental Health

Hypothesis testing helps in indicating the factors that may cause some serious mental health issues.   

4. Manufacturing

Testing whether the new change in the process of manufacturing helped in the improvement of the process as well as in the quantity or not.  In the same way, there are many other use cases that we get to see in different sectors for hypothesis testing. 

Error Terms in Hypothesis Testing

1. type-i error.

Type I error occurs during the process of hypothesis testing when the null hypothesis is rejected even though it is accurate. This kind of error is also known as False positive because even though the statement is positive or correct but results are given as false. For example, an innocent person still goes to jail because he is considered to be guilty.   

2. Type-II error

Type II error occurs during the process of hypothesis testing when the null hypothesis is not rejected even though it is inaccurate. This Kind of error is also called a False-negative which means even though the statements are false and inaccurate, it still says it is correct and doesn’t reject it. For example, a person is guilty, but in court, he has been proven innocent where he is guilty, so this is a Type II error.   

3. Level of Significance

The level of significance is majorly used to measure the confidence with which a null hypothesis can be rejected. It is the value with which one can reject the null hypothesis which is H0. The level of significance gauges whether the hypothesis testing is significant or not.   

P-value stands for probability value, which tells us the probability or likelihood to find the set of observations when the null hypothesis is true using statistical tests. The main purpose is to check the significance of the statistical statement.   

5. High P-Values

A higher P-value indicates that the testing is not statistically significant. For example, a P value greater than 0.05 is considered to be having higher P value. A higher P-value also means that our evidence and proofs are not strong enough to influence the population.

In hypothesis testing, each step is responsible for getting the outcomes and the results, whether it is the selection of statistical tests or working on data, each step contributes towards the better consequences of the hypothesis testing. It is always a recommendable step when planning for predicting the outcomes and trying to experiment with the sample; hypothesis testing is a useful concept to apply.   

Frequently Asked Questions (FAQs)

We can test a hypothesis by selecting a correct hypothetical test and, based on those getting results.   

Many statistical tests are used for hypothetical testing which includes Z-test, T-test, etc. 

Hypothesis helps us in doing various experiments and working on a specific research topic to predict the results.   

The null and alternative hypothesis, data collection, selecting a statistical test, selecting significance value, calculating p-value, check your findings.    

In simple words, parametric tests are purely based on assumptions whereas non-parametric tests are based on data that is collected and acquired from a sample.   

Gauri Guglani

Gauri Guglani works as a Data Analyst at Deloitte Consulting. She has done her major in Information Technology and holds great interest in the field of data science. She owns her technical skills as well as managerial skills and also is great at communicating. Since her undergraduate, Gauri has developed a profound interest in writing content and sharing her knowledge through the manual means of blog/article writing. She loves writing on topics affiliated with Statistics, Python Libraries, Machine Learning, Natural Language processes, and many more.

Avail your free 1:1 mentorship session.

Something went wrong

Upcoming Data Science Batches & Dates

• Search Search Please fill out this field.

What Is Hypothesis Testing?

• How It Works

4 Step Process

The bottom line.

• Fundamental Analysis

Hypothesis Testing: 4 Steps and Example

Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.

Key Takeaways

• Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
• The test provides evidence concerning the plausibility of the hypothesis, given the data.
• Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
• The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

How Hypothesis Testing Works

In hypothesis testing, an  analyst  tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.

The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.

• State the hypotheses.
• Formulate an analysis plan, which outlines how the data will be evaluated.
• Carry out the plan and analyze the sample data.
• Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.

Example of Hypothesis Testing

If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.

A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.

If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."

When Did Hypothesis Testing Begin?

Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”

What are the Benefits of Hypothesis Testing?

Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.

What are the Limitations of Hypothesis Testing?

Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.

Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

Sage. " Introduction to Hypothesis Testing ," Page 4.

Elder Research. " Who Invented the Null Hypothesis? "

Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples ."

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Teach yourself statistics

How to Analyze Survey Data for Hypothesis Tests

Traditionally, researchers analyze survey data to estimate population parameters. But very similar analytical techniques can also be applied to test hypotheses.

In this lesson, we describe how to analyze survey data to test statistical hypotheses.

The Logic of the Analysis

In a big-picture sense, the analysis of survey sampling data is easy. When you use sample data to test a hypothesis, the analysis includes the same seven steps:

• Estimate a population parameter.
• Estimate population variance.
• Compute standard error.
• Set the significance level.
• Find the critical value (often a z-score or a t-score).
• Define the upper limit of the region of acceptance.
• Define the lower limit of the region of acceptance.

It doesn't matter whether the sampling method is simple random sampling, stratified sampling, or cluster sampling. And it doesn't matter whether the parameter of interest is a mean score, a proportion, or a total score. The analysis of survey sampling data always includes the same seven steps.

However, formulas used in the first three steps of the analysis can differ, based on the sampling method and the parameter of interest. In the next section, we'll list the formulas to use for each step. By the end of the lesson, you'll know how to test hypotheses about mean scores, proportions, and total scores using data from simple random samples, stratified samples, and cluster samples.

Data Analysis for Hypothesis Testing

Now, let's look in a little more detail at the seven steps required to conduct a hypothesis test, when you are working with data from a survey sample.

Sample mean = x = Σx / n

where x is a sample estimate of the population mean, Σx is the sum of all the sample observations, and n is the number of sample observations.

Population total = t = N * x

where N is the number of observations in the population, and x is the sample mean.

Or, if we know the sample proportion, we can estimate the population total (t) as:

Population total = t = N * p

where t is an estimate of the number of elements in the population that have a specified attribute, N is the number of observations in the population, and p is the sample proportion.

Sample mean = x = Σ( N h / N ) * x h

where N h is the number of observations in stratum h of the population, N is the number of observations in the population, and x h is the mean score from the sample in stratum h .

Sample proportion = p = Σ( N h / N ) * p h

where N h is the number of observations in stratum h of the population, N is the number of observations in the population, and p h is the sample proportion in stratum h .

Population total = t = ΣN h * x h

where N h is the number of observations in the population from stratum h , and x h is the sample mean from stratum h .

Or if we know the population proportion in each stratum, we can use this formula to estimate a population total:

Population total = t = ΣN h * p h

where t is an estimate of the number of observations in the population that have a specified attribute, N h is the number of observations from stratum h in the population, and p h is the sample proportion from stratum h .

x = ( N / ( n * M ) ] * Σ ( M h * x h )

where N is the number of clusters in the population, n is the number of clusters in the sample, M is the number of observations in the population, M h is the number of observations in cluster h , and x h is the mean score from the sample in cluster h .

p = ( N / ( n * M ) ] * Σ ( M h * p h )

where N is the number of clusters in the population, n is the number of clusters in the sample, M is the number of observations in the population, M h is the number of observations in cluster h , and p h is the proportion from the sample in cluster h .

Population total = t = N/n * ΣM h * x h

where N is the number of clusters in the population, n is the number of clusters in the sample, M h is the number of observations in the population from cluster h , and x h is the sample mean from cluster h .

And, if we know the sample proportion for each cluster, we can estimate a population total:

Population total = t = N/n * ΣM h * p h

where t is an estimate of the number of elements in the population that have a specified attribute, N is the number of clusters in the population, n is the number of clusters in the sample, M h is the number of observations from cluster h in the population, and p h is the sample proportion from cluster h .

s 2 = P * (1 - P)

where s 2 is an estimate of population variance, and P is the value of the proportion in the null hypothesis.

s 2 = Σ ( x i - x ) 2 / ( n - 1 )

where s 2 is a sample estimate of population variance, x is the sample mean, x i is the i th element from the sample, and n is the number of elements in the sample.

s 2 h = Σ ( x i h - x h ) 2 / ( n h - 1 )

where s 2 h is a sample estimate of population variance in stratum h , x i h is the value of the i th element from stratum h, x h is the sample mean from stratum h , and n h is the number of sample observations from stratum h .

s 2 h = Σ ( x i h - x h ) 2 / ( m h - 1 )

where s 2 h is a sample estimate of population variance in cluster h , x i h is the value of the i th element from cluster h, x h is the sample mean from cluster h , and m h is the number of observations sampled from cluster h .

s 2 b = Σ ( t h - t/N ) 2 / ( n - 1 )

where s 2 b is a sample estimate of the variance between sampled clusters, t h is the total from cluster h, t is the sample estimate of the population total, N is the number of clusters in the population, and n is the number of clusters in the sample.

You can estimate the population total (t) from the following formula:

where M h is the number of observations in the population from cluster h , and x h is the sample mean from cluster h .

SE = sqrt [ (1 - n/N) * s 2 / n ]

where n is the sample size, N is the population size, and s is a sample estimate of the population standard deviation.

SE = sqrt [ N 2 * (1 - n/N) * s 2 / n ]

where N is the population size, n is the sample size, and s 2 is a sample estimate of the population variance.

SE = (1 / N) * sqrt { Σ [ N 2 h * ( 1 - n h /N h ) * s 2 h / n h ] }

where n h is the number of sample observations from stratum h, N h is the number of elements from stratum h in the population, N is the number of elements in the population, and s 2 h is a sample estimate of the population variance in stratum h.

SE = sqrt { Σ [ N 2 h * ( 1 - n h /N h ) * s 2 h / n h ] }

where N h is the number of elements from stratum h in the population, n h is the number of sample observations from stratum h, and s 2 h is a sample estimate of the population variance in stratum h.

where M is the number of observations in the population, N is the number of clusters in the population, n is the number of clusters in the sample, M h is the number of elements from cluster h in the population, m h is the number of elements from cluster h in the sample, x h is the sample mean from cluster h, s 2 h is a sample estimate of the population variance in stratum h, and t is a sample estimate of the population total. For the equation above, use the following formula to estimate the population total.

t = N/n * Σ M h x h

With one-stage cluster sampling, the formula for the standard error reduces to:

where M is the number of observations in the population, N is the number of clusters in the population, n is the number of clusters in the sample, M h is the number of elements from cluster h in the population, m h is the number of elements from cluster h in the sample, p h is the value of the proportion from cluster h, and t is a sample estimate of the population total. For the equation above, use the following formula to estimate the population total.

t = N/n * Σ M h p h

where N is the number of clusters in the population, n is the number of clusters in the sample, s 2 b is a sample estimate of the variance between clusters, m h is the number of elements from cluster h in the sample, M h is the number of elements from cluster h in the population, and s 2 h is a sample estimate of the population variance in cluster h.

SE = N * sqrt { [ ( 1 - n/N ) / n ] * s 2 b /n }

• Choose a significance level. The significance level (denoted by α) is the probability of committing a Type I error . Researchers often set the significance level equal to 0.05 or 0.01.

When the null hypothesis is two-tailed, the critical value is the z-score or t-score that has a cumulative probability equal to 1 - α/2. When the null hypothesis is one-tailed, the critical value has a cumulative probability equal to 1 - α.

Researchers use a t-score when sample size is small; a z-score when it is large (at least 30). You can use the Normal Distribution Calculator to find the critical z-score, and the t Distribution Calculator to find the critical t-score.

If you use a t-score, you will have to find the degrees of freedom (df). With simple random samples, df is often equal to the sample size minus one.

Note: The critical value for a one-tailed hypothesis does not equal the critical value for a two-tailed hypothesis. The critical value for a one-tailed hypothesis is smaller.

UL = M + SE * CV

• If the null hypothesis is μ > M: The theoretical upper limit of the region of acceptance is plus infinity, unless the parameter in the null hypothesis is a proportion or a percentage. The upper limit is 1 for a proportion, and 100 for a percentage.

LL = M - SE * CV

• If the null hypothesis is μ < M: The theoretical lower limit of the region of acceptance is minus infinity, unless the test statistic is a proportion or a percentage. The lower limit for a proportion or a percentage is zero.

The region of acceptance is the range of values between LL and UL. If the sample estimate of the population parameter falls outside the region of acceptance, the researcher rejects the null hypothesis. If the sample estimate falls within the region of acceptance, the researcher does not reject the null hypothesis.

By following the steps outlined above, you define the region of acceptance in such a way that the chance of making a Type I error is equal to the significance level .

Test Your Understanding

In this section, two hypothesis testing examples illustrate how to define the region of acceptance. The first problem shows a two-tailed test with a mean score; and the second problem, a one-tailed test with a proportion.

Sample Size Calculator

As you probably noticed, defining the region of acceptance can be complex and time-consuming. Stat Trek's Sample Size Calculator can do the same job quickly, easily, and error-free.The calculator is easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

An inventor has developed a new, energy-efficient lawn mower engine. He claims that the engine will run continuously for 5 hours (300 minutes) on a single ounce of regular gasoline. Suppose a random sample of 50 engines is tested. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes.

Consider the null hypothesis that the mean run time is 300 minutes against the alternative hypothesis that the mean run time is not 300 minutes. Use a 0.05 level of significance. Find the region of acceptance. Based on the region of acceptance, would you reject the null hypothesis?

Solution: The analysis of survey data to test a hypothesis takes seven steps. We work through those steps below:

However, if we had to compute the sample mean from raw data, we could do it, using the following formula:

where Σx is the sum of all the sample observations, and n is the number of sample observations.

If we hadn't been given the standard deviation, we could have computed it from the raw sample data, using the following formula:

For this problem, we know that the sample size is 50, and the standard deviation is 20. The population size is not stated explicitly; but, in theory, the manufacturer could produce an infinite number of motors. Therefore, the population size is a very large number. For the purpose of the analysis, we'll assume that the population size is 100,000. Plugging those values into the formula, we find that the standard error is:

SE = sqrt [ (1 - 50/100,000) * 20 2 / 50 ]

SE = sqrt(0.9995 * 8) = 2.828

• Choose a significance level. The significance level (α) is chosen for us in the problem. It is 0.05. (Researchers often set the significance level equal to 0.05 or 0.01.)

When the null hypothesis is two-tailed, the critical value has a cumulative probability equal to 1 - α/2. When the null hypothesis is one-tailed, the critical value has a cumulative probability equal to 1 - α.

For this problem, the null hypothesis and the alternative hypothesis can be expressed as:

Since this problem deals with a two-tailed hypothesis, the critical value will be the z-score that has a cumulative probability equal to 1 - α/2. Here, the significance level (α) is 0.05, so the critical value will be the z-score that has a cumulative probability equal to 0.975.

We use the Normal Distribution Calculator to find that the z-score with a cumulative probability of 0.975 is 1.96. Thus, the critical value is 1.96.

where M is the parameter value in the null hypothesis, SE is the standard error, and CV is the critical value. So, for this problem, we compute the lower limit of the region of acceptance as:

LL = 300 - 2.828 * 1.96

LL = 300 - 5.54

LL = 294.46

LL = 300 + 2.828 * 1.96

LL = 300 + 5.54

LL = 305.54

Thus, given a significance level of 0.05, the region of acceptance is range of values between 294.46 and 305.54. In the tests, the engines ran for an average of 295 minutes. That value is within the region of acceptance, so the inventor cannot reject the null hypothesis that the engines run for 300 minutes on an ounce of fuel.

Problem 2 Suppose the CEO of a large software company claims that at least 80 percent of the company's 1,000,000 customers are very satisfied. A survey of 100 randomly sampled customers finds that 73 percent are very satisfied. To test the CEO's hypothesis, find the region of acceptance. Assume a significance level of 0.05.

However, if we had to compute the sample proportion (p) from raw data, we could do it by using the following formula:

where s 2 is the population variance when the true population proportion is P, and P is the value of the proportion in the null hypothesis.

For the purpose of estimating population variance, we assume the null hypothesis is true. In this problem, the null hypothesis states that the true proportion of satisfied customers is 0.8. Therefore, to estimate population variance, we insert that value in the formula:

s 2 = 0.8 * (1 - 0.8)

s 2 = 0.8 * 0.2 = 0.16

For this problem, we know that the sample size is 100, the variance ( s 2 ) is 0.16, and the population size is 1,000,000. Plugging those values into the formula, we find that the standard error is:

SE = sqrt [ (1 - 100/1,000,000) * 0.16 / 100 ]

SE = sqrt(0.9999 * 0.0016) = 0.04

Since this problem deals with a one-tailed hypothesis, the critical value will be the z-score that has a cumulative probability equal to 1 - α. Here, the significance level (α) is 0.05, so the critical value will be the z-score that has a cumulative probability equal to 0.95.

We use the Normal Distribution Calculator to find that the z-score with a cumulative probability of 0.95 is 1.645. Thus, the critical value is 1.645.

LL = 0.8 - 0.04 * 1.645

LL = 0.8 - 0.0658 = 0.7342

• Find the upper limit of the region of acceptance. For this type of one-tailed hypothesis, the theoretical upper limit of the region of acceptance is 1; since any proportion greater than 0.8 is consistent with the null hypothesis, and 1 is the largest value that a proportion can have.

Thus, given a significance level of 0.05, the region of acceptance is the range of values between 0.7342 and 1.0. In the sample survey, the proportion of satisfied customers was 0.73. That value is outside the region of acceptance, so null hypothesis must be rejected.

Statistics Made Easy

5 Tips for Interpreting P-Values Correctly in Hypothesis Testing

Hypothesis testing is a critical part of statistical analysis and is often the endpoint where conclusions are drawn about larger populations based on a sample or experimental dataset. Central to this process is the p-value. Broadly, the p-value quantifies the strength of evidence against the null hypothesis. Given the importance of the p-value, it is essential to ensure its interpretation is correct. Here are five essential tips for ensuring the p-value from a hypothesis test is understood correctly. 

1. Know What the P-value Represents

First, it is essential to understand what a p-value is. In hypothesis testing, the p-value is defined as the probability of observing your data, or data more extreme, if the null hypothesis is true. As a reminder, the null hypothesis states no difference between your data and the expected population. 

For example, in a hypothesis test to see if changing a company’s logo drives more traffic to the website, a null hypothesis would state that the new traffic numbers are equal to the old traffic numbers. In this context, the p-value would be the probability that the data you observed, or data more extreme, would occur if this null hypothesis were true. 

Therefore, a smaller p-value indicates that what you observed is unlikely to have occurred if the null were true, offering evidence to reject the null hypothesis. Typically, a cut-off value of 0.05 is used where any p-value below this is considered significant evidence against the null. 

2. Understand the Directionality of Your Hypothesis

Based on the research question under exploration, there are two types of hypotheses: one-sided and two-sided. A one-sided test specifies a particular direction of effect, such as traffic to a website increasing after a design change. On the other hand, a two-sided test allows the change to be in either direction and is effective when the researcher wants to see any effect of the change. 

Either way, determining the statistical significance of a p-value is the same: if the p-value is below a threshold value, it is statistically significant. However, when calculating the p-value, it is important to ensure the correct sided calculations have been completed. 

Additionally, the interpretation of the meaning of a p-value will differ based on the directionality of the hypothesis. If a one-sided test is significant, the researchers can use the p-value to support a statistically significant increase or decrease based on the direction of the test. If a two-sided test is significant, the p-value can only be used to say that the two groups are different, but not that one is necessarily greater. 

3. Avoid Threshold Thinking

A common pitfall in interpreting p-values is falling into the threshold thinking trap. The most commonly used cut-off value for whether a calculated p-value is statistically significant is 0.05. Typically, a p-value of less than 0.05 is considered statistically significant evidence against the null hypothesis. 

However, this is just an arbitrary value. Rigid adherence to this or any other predefined cut-off value can obscure business-relevant effect sizes. For example, a hypothesis test looking at changes in traffic after a website design may find that an increase of 10,000 views is not statistically significant with a p-value of 0.055 since that value is above 0.05. However, the actual increase of 10,000 may be important to the growth of the business. 

Therefore, a p-value can be practically significant while not being statistically significant. Both types of significance and the broader context of the hypothesis test should be considered when making a final interpretation. 

4. Consider the Power of Your Study

Similarly, some study conditions can result in a non-significant p-value even if practical significance exists. Statistical power is the ability of a study to detect an effect when it truly exists. In other words, it is the probability that the null hypothesis will be rejected when it is false. 

Power is impacted by a lot of factors. These include sample size, the effect size you are looking for, and variability within the data. In the example of website traffic after a design change, if the number of visits overall is too small, there may not be enough views to have enough power to detect a difference. 

Simple ways to increase the power of a hypothesis test and increase the chances of detecting an effect are increasing the sample size, looking for a smaller effect size, changing the experiment design to control for variables that can increase variability, or adjusting the type of statistical test being run.

5. Be Aware of Multiple Comparisons

Whenever multiple p-values are calculated in a single study due to multiple comparisons, there is an increased risk of false positives. This is because each individual comparison introduces random fluctuations, and each additional comparison compounds these fluctuations. 

For example, in a hypothesis test looking at traffic before and after a website redesign, the team may be interested in making more than one comparison. This can include total visits, page views, and average time spent on the website. Since multiple comparisons are being made, there must be a correction made when interpreting the p-value. 

The Bonferroni correction is one of the most commonly used methods to account for this increased probability of false positives. In this method, the significance cut-off value, typically 0.05, is divided by the number of comparisons made. The result is used as the new significance cut-off value.  Applying this correction mitigates the risk of false positives and improves the reliability of findings from a hypothesis test. 

In conclusion, interpreting p-values requires a nuanced understanding of many statistical concepts and careful consideration of the hypothesis test’s context. By following these five tips, the interpretation of the p-value from a hypothesis test can be more accurate and reliable, leading to better data-driven decision-making.

Featured Posts

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Data Analysis with Python

Introduction to Data Analysis

• What is Data Analysis?
• Data Analytics and its type
• How to Install Numpy on Windows?
• How to Install Pandas in Python?
• How to Install Matplotlib on python?
• How to Install Python Tensorflow in Windows?

Data Analysis Libraries

• Pandas Tutorial
• NumPy Tutorial - Python Library
• Data Analysis with SciPy
• Introduction to TensorFlow

Data Visulization Libraries

• Matplotlib Tutorial
• Python Seaborn Tutorial
• Plotly tutorial
• Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

• Univariate, Bivariate and Multivariate data and its analysis
• Measures of Central Tendency in Statistics
• Measures of spread - Range, Variance, and Standard Deviation
• Interquartile Range and Quartile Deviation using NumPy and SciPy
• Anova Formula
• Skewness of Statistical Data
• How to Calculate Skewness and Kurtosis in Python?
• Difference Between Skewness and Kurtosis
• Histogram | Meaning, Example, Types and Steps to Draw
• Interpretations of Histogram
• Quantile Quantile plots
• What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
• Using pandas crosstab to create a bar plot
• Exploring Correlation in Python
• Mathematics | Covariance and Correlation
• Factor Analysis | Data Analysis
• Data Mining - Cluster Analysis
• MANOVA Test in R Programming
• Python - Central Limit Theorem
• Probability Distribution Function
• Probability Density Estimation & Maximum Likelihood Estimation
• Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Poisson Distribution | Definition, Formula, Table and Examples
• P-Value: Comprehensive Guide to Understand, Apply, and Interpret
• Z-Score in Statistics
• How to Calculate Point Estimates in R?
• Confidence Interval
• Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

• ML | Data Preprocessing in Python
• ML | Overview of Data Cleaning
• ML | Handling Missing Values
• Detect and Remove the Outliers using Python

Data Transformation

• Data Normalization Machine Learning
• Sampling distribution Using Python

Time Series Data Analysis

• Data Mining - Time-Series, Symbolic and Biological Sequences Data
• Basic DateTime Operations in Python
• Time Series Analysis & Visualization in Python
• How to deal with missing values in a Timeseries in Python?
• How to calculate MOVING AVERAGE in a Pandas DataFrame?
• What is a trend in time series?
• How to Perform an Augmented Dickey-Fuller Test in R
• AutoCorrelation

Case Studies and Projects

• Top 8 Free Dataset Sources to Use for Data Science Projects
• Step by Step Predictive Analysis - Machine Learning
• 6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. 

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Key Terms of Hypothesis Testing

• P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
• Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
• Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
• Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing. 

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

• Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
• t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
• Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
• F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

• If Test Statistic>Critical Value: Reject the null hypothesis.
• If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

• μ represents the population mean, 
• σ is the standard deviation
• and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

• t = t-score,
• x̄ = sample mean
• μ = population mean,
• s = standard deviation of the sample,
• n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

• i,j are the rows and columns index respectively.

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

• Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
• After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

• Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
• Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

• m  = mean of the difference i.e X after, X before
• s  = standard deviation of the difference (d) i.e d i ​= X after, i ​− X before,
• n  = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

• If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
• If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05. 

• The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
• The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

• Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
• Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

• Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
• The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
• Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Similar reads.

• data-science
• Data Science
• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• All Products

Hypothesis Testing - One Way Analysis of Variance (ANOVA) with F-Test

This article describes how to perform a one-way ANOVA with F-test.

To learn about statistical functions in MAQL, see our Documentation .

In Hypothesis Testing - One Sample T-Tests and Z-Tests , we examined comparisons of a single sample mean with the population mean. For situations in which three or more sample means are compared with each other, the ANOVA test can be used to measure statistically significant differences among those means and, in turn, among the means for their populations.

ANOVA should be viewed as an extension of the t-test when there are more than two comparison groups.

The size of a difference that is statistically significant depends on the sample sizes and the amount of certainty desired in the testing. In our significance tests, we use p-values (levels of statistical significance).

For example, a company’s marketing team may want to answer, “Does the day of the week have an impact on the number of clicks?” To frame the question in other terms, we wish to measure whether there is any difference between the number of clicks on different days of the week.

The first step of any hypothesis testing is to convert the question into null and alternative hypotheses:

• null hypothesis (H0): x? Mon = x? Tue = x? Wed = x? Thu = x? Fri = x? Sat = x? Sun (where x? is the average number of clicks in a given day of the week). If the average number of clicks on each day of the week is consistent, the day of the week does not have an impact.
• alternative hypothesis (H1): At least one of the mean values does not equal the others.

To perform this test, we must calculate the F-test statistical value and compare it with the critical value from the F-distribution table, based on the chosen significance level or p-value (usually 0.05) and the degrees of freedom.

Computing ANOVA Table

An ANOVA table comprises the following components:

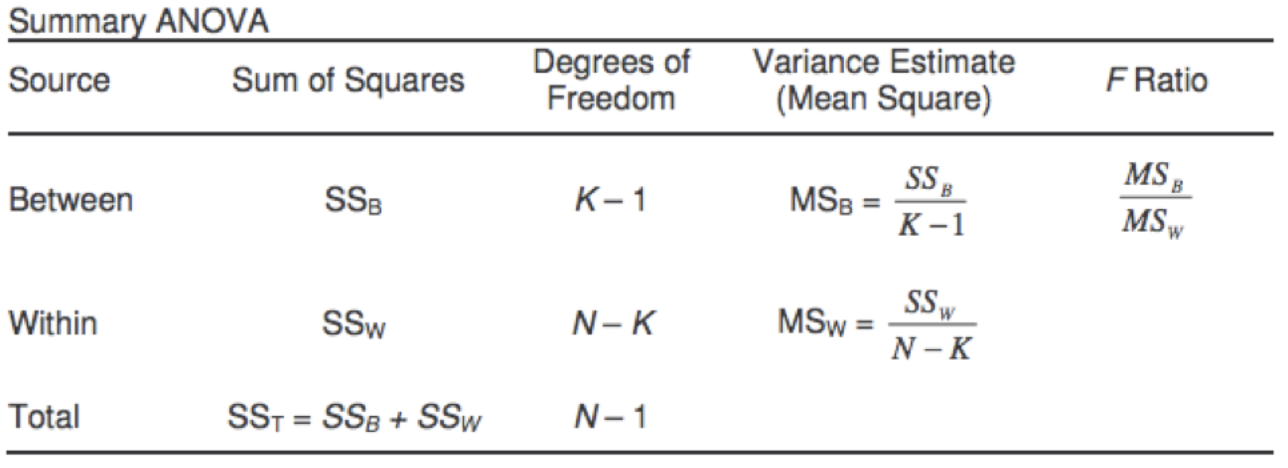
Our goal is to calculate the value of F Ratio in the last column as the final result of computing the values in all of the other columns. Let’s review what these table values mean and how we can calculate them in MAQL.

Column 1 - Sum of Squares

SS B = ∑n( x? i -μ)², is the Sum of Squares (deviations) between the group means and the grand mean, where *x?*i is the group mean and μ represents the grand mean.

Avg Clicks(Mon) The following MAQL metric computes the average number of clicks for the specified day of the week: SELECT AVG( Clicks ) WHERE Day of Week (Mon-Sun) (Date) =Mon We calculate this metric for each day of the week. These are our group means (*x?*i).

Avg Clicks(ALL) The following MAQL calculates the average clicks across all days of the week. This value is our grand mean (μ). SELECT AVG( Clicks ) BY ALL OTHER

Count(Mon) The following metric calculates the count of clicks for Monday: SELECT COUNT( Date(Date) , Records of Website ) WHERE Day of Week (Mon-Sun) (Date) =Mon We calculate this metric for each day of the week to get the number of records in each group. In our example, the unique identifier for clicks is the Date attribute.

Dev(B,Mon) (The B above stands for “Between”) SELECT ( Avg Clicks(Mon) - Avg Clicks(ALL) ) BY ALL OTHER This metric gives us the deviation between the groups and the grand mean (*x?*i-μ). We calculate this for each day of the week.

SSB Finally, we add n (x?i-μ) for all the groups to get the value for SSB. SELECT ((POWER( Dev(B,Mon) ,2)* Count(Mon) ) + ((POWER( Dev(B,Tue) ,2)* Count(Tue) ) + ((POWER(Dev(B,Wed) ,2)* Count(Wed) ) ...

SST SS T = ∑(xi -μ)² is the Sum of Squares of all the observations from the grand mean (μ), regardless of which group produced them. SELECT SUM(POWER((SELECT (SUM( Clicks )- Avg Clicks(ALL) ) BY Date (Date) ),2)) Note how we used the BY Date(Date) clause to compute the difference between each observation and the grand mean. In our example, Date is the unique identifier for Clicks.

SSW SS W = SS T - SS B , is the Sum of Squares within the groups. It is also called Error Sum of Squares and can be calculated by subtracting Sum of Squares between the groups from total Sum of Squares. SELECT SST - SSB

Column 2 - Degrees of Freedom

K-1 measures the degrees of freedom between groups, where K is number of groups. In this example, the value is 7 because we are analyzing days of the week.

N-K measures within degrees of freedom, where N is total number of records.

Count(N) SELECT COUNT( Date(Date) , Records of Website )

Column 3 - Mean Square

MS B = SS B / K-1 is the Mean Sum of Squares between the groups. It is calculated by dividing the Sum of Squares between the groups by the between-group degrees of freedom.

MSB SELECT SSB / ( K -1)

MS W = SS W / N-K is the Mean Sum of Squares within the group. It is calculated by dividing the Sum of Squares within the groups by the within-group degrees of freedom.

MSW SELECT SSW / ( Count(N) - K )

Column 4 - F Ratio

F Ratio = MS B / MS W SELECT MSB / MSW

After we have calculated the F-value, we can compare it to the critical value using an F-distribution table and then evaluate the significance of the analysis.

Evaluating Significance

F-Distribution Table

The first step is to upload a table of F-distribution critical values, which you can find in any statistical textbook. Download an example table of F-statistic values in the attached file. The example table has 4 columns:

df1 - Between-group degrees of freedom

df2 - Within-group degrees of freedom

alpha - Significance level that we desire in our analysis (usually 0.05, 0.01, 0.005)

X - This column contains the critical value of F-statistic. We compare the F Ratio metric calculated above with this value using the other three columns as lookup values

Fact Dataset in LDM

We create a fact dataset in our logical data model, as shown below, to store these values:

Note that all the four columns are stored as facts.

Upload F-Distribution Data

After you have created the dataset in your logical data model, build a simple ETL graph to upload the data in the file to your project.

Calculate Metrics

After the values have been uploaded to the project, we can use the following metrics to evaluate whether our analysis is significant.

df1(Clicks) SELECT CASE WHEN ( K -1) > 150 THEN 1000, WHEN ( K -1) > 90 THEN 120, WHEN ( K -1) > 50 THEN 60,WHEN ( K -1) > 35 THEN 40, WHEN ( K -1) > 29 THEN 30 ELSE ( K -1) END

df2(Clicks) SELECT CASE WHEN (COUNT(N)-K) > 150 THEN 1000, WHEN (COUNT(N)-K) > 90 THEN 120, WHEN(COUNT(N)-K) > 50 THEN 60,WHEN (COUNT(N)-K) > 35 THEN 40, WHEN (COUNT(N)-K) > 29 THEN 30 ELSE (COUNT(N)-K) END

X(Clicks) SELECT (SELECT SUM( X ) WHERE df1 = df1(Clicks) AND df2 = df2(Clicks) AND alpha = Sig Level ) BY ALL OTHER

The Sig Level variable is used to depict significance level, which is usually 0.05 or 0.01.

• If the F Ratio metric is larger than this X value, our analysis is significant.
• If the analysis is valid, we can reject the null hypothesis. In our example, day of the week does have an impact on the number of clicks.

A computational model for sample dependence in hypothesis testing of genome data

• Original Paper - Cross-Disciplinary Physics and Related Areas of Science and Technology
• Published: 30 May 2024

Cite this article

• Sunhee Kim   ORCID: orcid.org/0000-0002-9525-3179 1 &
• Chang-Yong Lee   ORCID: orcid.org/0000-0003-1778-6532 1  

Statistical hypothesis testing assumes that the samples being analyzed are statistically independent, meaning that the occurrence of one sample does not affect the probability of the occurrence of another. In reality, however, this assumption may not always hold. When samples are not independent, it is important to consider their interdependence when interpreting the results of the hypothesis test. In this study, we address the issue of sample dependence in hypothesis testing by introducing the concept of adjusted sample size. This adjusted sample size provides additional information about the test results, which is particularly useful when samples exhibit dependence. To determine the adjusted sample size, we use the theory of networks to quantify sample dependence and model the variance of network density as a function of sample size. Our approach involves estimating the adjusted sample size by analyzing the variance of the network density, which reflects the degree of sample dependence. Through simulations, we demonstrate that dependent samples yield a higher variance in network density compared to independent samples, validating our method for estimating the adjusted sample size. Furthermore, we apply our proposed method to genomic datasets, estimating the adjusted sample size to effectively account for sample dependence in hypothesis testing. This guides interpreting test results and ensures more accurate data analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Code and script availability

We have released our analysis tool, a detailed script of the sampling procedure, input files, and output files so that anyone can reproduce the results. These are available at https://github.com/infoLab204/adj_size .

W. Finch, J. Bolin, K. Kelley, Multilevel Modeling Using R (Chapman and Hall/CRC, 2014)

Google Scholar  

E. Gómez-de-Mariscal, V. Guerrero, A. Sneider et al., Sci. Rep. 11 , 20942 (2021). https://doi.org/10.1038/s41598-021-00199-5

Article   ADS   Google Scholar  

K. Stewart, Encyclopedia of Quality of Life and Well-Being Research (Springer, New York, 2014), pp.6462–6464

Book   Google Scholar  

I. Park, H. Lee, Stat. Can. 30 , 183 (2004)

L. Kish, Survey Sampling (John Wiley, New York, 1965)

M. Lin, H. Lucas Jr., G. Shmueli, Inf. Syst. Res. 24 , 906 (2013). https://doi.org/10.1287/isre.2013.0480

Article   Google Scholar  

A. Barabási, Network Science (Cambridge University Press, Cambridge, 2016)

S. Kim, J. Yun, J. Korean Phys. Soc. 81 , 697 (2022). https://doi.org/10.1007/s40042-022-00590-z

H. Jo, J. Korean Phys. Soc. 82 , 430 (2023). https://doi.org/10.1007/s40042-022-00675-9

R. Nelsen, An Introduction to Copulas (Springer, New York, 1999)

D. Tjøstheim, H. Otneim, B. Støve, Statistical Modeling Using Local Gaussian Approximation (Academic Press, Cambridge, 2021), pp.135–159

D. Lewandowski, D. Kurowicka, H. Joe, J. Multivar. Anal. 100 , 1989 (2009). https://doi.org/10.1016/j.jmva.2009.04.008

K. Zhao, C. Tung et al., Nat. Commun. 13 , 467 (2011). https://doi.org/10.1038/ncomms1467

K. Kim, B. Nawade et al., Front. Plant Sci. 13 , 1036177 (2022). https://doi.org/10.3389/fpls.2022.1036177

K. Zhao, 44K SNP set. (Rice Diversity), http://ricediversity.org/data/index.cfm. Accessed 13 Apr 2024

K. Kim, Data Sheet 1.xlsx (850K_KNU data), https://www.frontiersin.org/articles/10.3389/fpls.2022.1036177/full#supplementary-material. Accessed 13 Apr 2024

W. Qiu, H. Joe, rcorrmatrix (cluster generation) https://rdrr.io/cran/clusterGeneration/man/rcorrmatrix.html. Accessed 13 Apr 2024

W. Press, S. Teukolsky, W. Vetterling, B. Flannery, Numerical Recipes in C: The Art of Scientific Computing , 2nd edn. (Cambridge University Press, Cambridge, 1992), pp.699–706

S. Besenbacher, T. Mailund, M. Schierup, Genetics 181 , 747 (2009). https://doi.org/10.1534/genetics.108.092643

A. Edwards, Genetics 179 , 1143 (2008). https://doi.org/10.1534/genetics.104.92940

G. Di Leo, F. Sardanelli, Eur. Radiol. Exp. 4 , 18 (2020). https://doi.org/10.1186/s41747-020-0145-y

C. Lee, Comput. Biol. Chem. 64 , 94 (2016). https://doi.org/10.1016/j.compbiolchem.2016.06.003

Article   MathSciNet   Google Scholar  

C. Kelley, Iterative Methods for Linear and Nonlinear Equations (SIAM, Philadelphia, 1995)

J. Myers, A. Well, Research Design and Statistical Analysis , 2nd edn. (Lawrence Erlbaum, Mahwah, 2003)

A. Brophy, Behav. Res. Methods 18 , 45 (1986). https://doi.org/10.3758/BF03200993

R-core, cor.test.R (stats package) https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/cor.test. Accessed 13 Apr 2024

S. Stigler, Ann. Statist. 9 , 465 (1981). https://doi.org/10.1214/aos/1176345451

R. Burden, J. Faires, Numerical Analysis , 9th edn. (Brooks/cole, Pacific Grove, 2010)

Download references

Acknowledgements

We are very grateful to Prof. Yong-Jin Park and Dr. Sang-Ho Chu for providing us with the 580K_KNU datasets. This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korean government(MSIT) (No. 2022R1A4A1030348), (No. 2021R1I1A3044289), and by the research grant of the Kongju National University in 2021.

Author information

Authors and affiliations.

The Department of Industrial Engineering, Kongju National University, Cheonan, 31080, Republic of Korea

Sunhee Kim & Chang-Yong Lee

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Chang-Yong Lee .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (PDF 217 KB)

Rights and permissions.

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Kim, S., Lee, CY. A computational model for sample dependence in hypothesis testing of genome data. J. Korean Phys. Soc. (2024). https://doi.org/10.1007/s40042-024-01100-z

Download citation

Received : 15 April 2024

Revised : 07 May 2024

Accepted : 16 May 2024

Published : 30 May 2024

DOI : https://doi.org/10.1007/s40042-024-01100-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Sample dependence
• Hypothesis testing
• Adjusted sample size
• Find a journal
• Publish with us
• Track your research