the intact one
Read MBA, BBA, B.COM Notes

Unbalanced Assignment Problems
Whenever the cost matrix of an assignment problem is not a square matrix, that is, whenever the number of sources is not equal to the number of destinations, the assignment problem is called an unbalanced assignment problem. In such problems, dummy rows (or columns) are added in the matrix so as to complete it to form a square matrix. The dummy rows or columns will contain all costs elements as zeroes. The Hungarian method may be used to solve the problem.
Example : A company has five machines that are used for four jobs. Each job can be assigned to one and only one machine. The cost of each job on each machine is given in the following Table.
Unbalanced Maximization Assignment problem example
Assignment Problem

Solution: Convert the 4 × 5 matrix into a square matrix by adding a dummy row D5.
Dummy Row D5 Added

Row-wise Reduction of the Matrix

Column-wise reduction is not necessary since all columns contain a single zero. Now, draw minimum number of lines to cover all the zeros, as shown in Table.
All Zeros in the Matrix Covered

Number of lines drawn ≠ Order of matrix. Hence not optimal.
Select the least uncovered element, i.e., 1, subtract it from other uncovered elements, add to the elements at intersection of lines and leave the elements that are covered with single line unchanged as shown in Table.
Subtracted or Added to Elements

Again Added or Subtracted 1 from Elements

Number of lines drawn = Order of matrix. Hence optimality is reached. Now assign the jobs to machines, as shown in Table.
Assigning Jobs to Machines

Example : In a plant layout, four different machines M1, M2, M3 and M4 are to be erected in a machine shop. There are five vacant areas A, B, C, D and E. Because of limited space, Machine M2 cannot be erected at area C and Machine M4 cannot be erected at area A. The cost of erection of machines is given in the Table.

Find the optimal assignment plan.
Solution: As the given matrix is not balanced, add a dummy row D5 with zero cost values. Assign a high cost H for (M2, C) and (M4, A). While selecting the lowest cost element neglect the high cost assigned H, as shown in Table below.

– Row-wise reduction of the matrix is shown in Table.
Matrix Reduced Row-wise

Note: Column-wise reduction is not necessary, as each column has at least one single zero. Now, draw minimum number of lines to cover all the zeros, see Table.
Lines Drawn to Cover all Zeros

Number of lines drawn ≠ Order of matrix. Hence not Optimal. Select the smallest uncovered element, in this case 1. Subtract 1 from all other uncovered element and add 1 with the elements at the intersection. The element covered by single line remains unchanged. These changes are shown in Table. Now try to draw minimum number of lines to cover all the zeros.
Added or Subtracted 1 from Elements

Now number of lines drawn = Order of matrix, hence optimality is reached. Optimal assignment of machines to areas are shown in Table.
Optimal Assignment

Hence, the optimal solution is:

Share this:
You might also like, role of ai and robotics in marketing, kmbnmk01 consumer behaviour and marketing communication, negotiable instruments (ni) act 1881: presentment of ni, 2 thoughts on “ unbalanced assignment problems ”.
- Pingback: GGSIPU(NEW DELHI) QUANTITATIVE TECHNIQUE – 2ND SEMESTER – STUDY MBA & BBA NOTES
- Pingback: CCSU(BBA) 406 Operation Research – Home | Management
Leave a Reply Cancel reply
Linear assignment with non-perfect matching
Dec 8, 2020
The linear assignment problem (or simply assignment problem) is the problem of finding a matching between two sets that minimizes the sum of pair-wise assignment costs. This can be expressed as finding a matching (or independent edge set) in a bipartite graph \(G = (U, V, E)\) that minimizes the sum of edge weights. The edge weights may be positive or negative and the bipartite graph does not need to be complete : if there is no edge between two vertices then they cannot be associated. Note that a maximum-weight assignment can be obtained by negating the weights and finding a minimum-weight assignment.
The simplest form of the assignment problem assumes that the bipartite graph is balanced (the two sets of vertices are the same size) and that there exists a perfect matching (in which every vertex has a match). Let \(n\) be the number of elements in each set and let \(C\) be a square matrix of size \(n \times n\) that contains the edge weights. Missing edges are represented by \(\infty\), such that \(C_{i j} < \infty \Leftrightarrow (i, j) \in E\). The assignment problem can then be clearly expressed as an integer linear program : (note that the problem is not actually solved using a general-purpose ILP solver, it is just a convenient framework in which to express the problem)
The constraint that the sum of each row and column is equal to one ensures that each element has exactly one match. However, what happens when the graph is not balanced or does not contain a perfect matching? We cannot enforce the sums to be equal to one. Which problem should be solved?
I recommend reading the tech report “On Minimum-Cost Assignments in Unbalanced Bipartite Graphs” by Lyle Ramshaw and Robert E. Tarjan. I will summarize some of the main points here.
Let us consider a more general, rectangular problem of size \(r \times n\) and assume (without loss of generality) that \(r \le n\). If \(r = n\) then the problem is balanced, if \(r < n\) it is unbalanced.
Clearly an unbalanced probem cannot have a perfect matching, since there will be at least \(n - r\) unmatched elements in the larger set. However, it may be possible to find a matching in which every vertex in the smaller set has a match. This is referred to as a one-sided perfect matching and the optimization problem can be expressed:
The inequality constraints enforce that each element in the smaller set has exactly one match while each element in the larger set has at most one match. Ramshaw and Tarjan outline a method to reduce from an unbalanced problem to a balanced problem while preserving sparsity. A simple alternative is to add \(n - r\) rows of zeros and then exclude these edges from the eventual solution. Most libraries for the assignment problem solve either the balanced or unbalanced version of this problem (see the later section).
However, whether balanced or unbalanced, it may still occur that the constraint set is infeasible, meaning that there does not exist a (one-sided) perfect matching. Let \(\nu(W) \le r\) denote the size of the largest matching in the graph. If \(\nu(W) < r\), then there does not exist a one-sided perfect matching and all possible matchings are imperfect.
Ramshaw and Tarjan actually outline three different versions of the assignment problem:
- perfect matching
- imperfect matching
- minimum-weight matching
The imperfect matching problem is to find the matching of size \(\nu(G)\) with the minimum cost. The minimum-weight matching problem is to find the matching of any size with the minimum cost. If \(\nu(G) = r = n\), then perfect and imperfect matching coincide. Otherwise, when \(\nu(G) < n\), there does not exist a perfect matching.
The imperfect matching problem can be expressed
and the minimum-weight matching problem can be expressed
Ramshaw and Tarjan show that both of these problems can be reduced to finding a perfect matching in a balanced graph. When using linear assignment, we should carefully consider which of the three problems we actually want to solve.
In support of minimum-weight matching
The minimum-weight matching problem is often the most natural choice, since it puts no constraint on the size of the matching. To illustrate the difference between this and the other problems, consider the following balanced problem:
The solution to perfect (or imperfect) matching is to choose -1 and -2 for a total score of -3 and a cardinality of 2. The solution to minimum-weight matching is to choose -4 with a cardinality of 1.
Minimum-weight matching will never select an edge with positive cost: it is better to simply leave it unselected. Edges with zero cost have no impact.
It may be more natural to consider the maximization of positive weights than the minimization of negative costs.
Min-cost imperfect matching with positive weights
Be careful when solving imperfect matching problems with positive edge weights! I would avoid this situation altogether due to the tension that exists between maximizing the number of matches and minimizing the sum of (positive) costs. This may result in the unexpected behaviour that adding an edge to the graph increases the minimum cost. For example, compare the following two problems:
Quick and dirty transformations
Ramshaw and Tarjan above describes some clever techniques to transform imperfect and minimum-weight matching problems into perfect matching problems while preserving sparsity. Here we describe some quick and dirty alternatives.
We can always transform an unbalanced (and therefore imperfect) problem into a balanced problem by adding \(n - r\) rows of zeros. The resulting balanced graph has a perfect matching if and only if the original unbalanced graph had a matching of size \(r\) (in which every vertex in the smaller set is matched).
If we need to solve imperfect matching but we only have a solver for perfect matching, it suffices to replace the infinite edge weights with a large, finite cost (e.g. larger than the total absolute value of all weights). The resulting graph must contain a perfect matching since it is a complete bipartite graph, and each high-cost edge is worth more than all original edges combined. The high-cost edges can be excluded at the end.
Most existing packages either solve perfect, one-sided perfect or imperfect matching. To use one of these solvers for the minimum-weight matching problem, it suffices to replace all positive edges (including infinite edges) with zero. If using a solver that leverages sparsity, it is better to use the technique described by Ramshaw and Tarjan.
Python packages
The table below outlines the different behaviour of several popular packages. The code that was used to determine the behaviour is available as a Jupyter notebook .
| Module | Function | Behaviour |
|---|---|---|
| Requires that problem is balanced (or else raises an exception). Requires that a perfect matching exists (or else returns infinite cost). | ||
| Supports unbalanced problems (with ; although check issues , ). Requires that a one-sided perfect matching exists (or else returns infinite cost). | ||
| Supports unbalanced problems. Requires that a one-sided perfect matching exists (or else raises an exception). | ||
| Supports unbalanced problems. Supports imperfect matching. | ||
| Requires problem is balanced. Requires that a perfect matching exists (or else raises an exception). Requires that costs are integer-valued. |
Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey
Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.
There are also live events, courses curated by job role, and more.
UNBALANCED ASSIGNMENT PROBLEM
Unbalanced Assignment problem is an assignment problem where the number of facilities is not equal to the number of jobs. To make unbalanced assignment problem, a balanced one, a dummy facility(s) or a dummy job(s) (as the case may be) is introduced with zero cost or time.
Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
Don’t leave empty-handed
Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.
It’s yours, free.

Check it out now on O’Reilly
Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Unbalanced Assignment Problem
In the previous section, the number of persons and the number of jobs were assumed to be the same. In this section, we remove this assumption and consider a situation where the number of persons is not equal to the number of jobs . In all such cases, fictitious rows and/or columns are added in the matrix to make it a square matrix.
- Maximization Problem
- Multiple Optimal Solutions
Example: Unbalanced Assignment Problem
| Job | ||||
|---|---|---|---|---|
| Person | 1 | 2 | 3 | 4 |
| A | 20 | 25 | 22 | 28 |
| B | 15 | 18 | 23 | 17 |
| C | 19 | 17 | 21 | 24 |
Since the number of persons is less than the number of jobs, we introduce a dummy person (D) with zero values. The revised assignment problem is given below:
Use Horizontal Scrollbar to View Full Table Calculation.
| Job | ||||
|---|---|---|---|---|
| Person | 1 | 2 | 3 | 4 |
| A | 20 | 25 | 22 | 28 |
| B | 15 | 18 | 23 | 17 |
| C | 19 | 17 | 21 | 24 |
| D (dummy) | 0 | 0 | 0 | 0 |
Now use the Hungarian method to obtain the optimal solution yourself. Ans. = 20 + 17 + 17 + 0 = 54.
Share and Recommend
Operations Research Simplified Back Next
Goal programming Linear programming Simplex Method Transportation Problem
Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.
Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
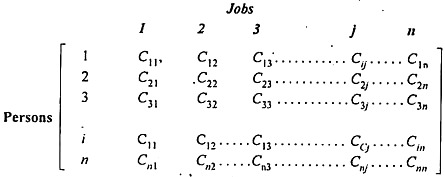
- DOI: 10.4236/AJOR.2016.64028
- Corpus ID: 124980289
Solving the Unbalanced Assignment Problem: Simpler Is Better
- Nathan K. Betts , Francis J. Vasko
- Published 24 June 2016
- Mathematics
- American Journal of Operations Research
Tables from this paper

8 Citations
An amalgamated approach for solving unbalanced assignment problem, modified hungarian method for unbalanced assignment problem with multiple jobs, modified hungarian method for solving balanced fuzzy transportation problems.
- Highly Influenced
Application of WinQSB for Assignment Models
A general statistical physics framework for assignment problems, where will the next emergency event occur predicting ambulance demand in emergency medical services using artificial intelligence, novel optimization method for unbalanced assignment problems with multiple jobs: the dhouib-matrix-ap2, graph based twin cost matrices for unbalanced assignment problem with improved ant colony algorithm, 6 references, a new approach of solving single objective unbalanced assignment problem.
- Highly Influential
Operations research : applications and algorithms
The hungarian method for the assignment problem, introduction to operations research, a lexisearch approach to some combinatorial programming problems, related papers.
Showing 1 through 3 of 0 Related Papers
Academia.edu no longer supports Internet Explorer.
To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .
Enter the email address you signed up with and we'll email you a reset link.
- We're Hiring!
- Help Center

Solving the Unbalanced Assignment Problem: Simpler Is Better

American Journal of Operations Research
Related Papers
Dr Avanish Kumar
Bhausaheb G Kore
In this paper I have proposed a new approach to solve an unbalanced assignment problem (UBAP). This approach includes two parts. First is to obtain an initial basic feasible solution (IBFS) and second part is to test optimality of an IBFS. I have proposed two new methods Row Penalty Assignment Method (RPAM) and Column Penalty Assignment Method (CPAM) to obtain an IBFS of an UBAP. Also I have proposed a new method Non-basic Smallest Effectiveness Method (NBSEM) to test optimality of an IBFS. We can solve an assignment problem of maximization type using this new approach in opposite sense. By this new approach, we achieve the goal with less number of computations and steps. Further we illustrate the new approach by suitable examples. INTRODUCTION The assignment problem is a special case of the transportation problem where the resources are being allocated to the activities on a one-to-one basis. Thus, each resource (e.g. an employee, machine or time slot) is to be assigned uniquely to a particular activity (e.g. a task, site or event). In assignment problems, supply in each row represents the availability of a resource such as a man, machine, vehicle, product, salesman, etc. and demand in each column represents different activities to be performed such as jobs, routes, factories, areas, etc. for each of which only one man or vehicle or product or salesman respectively is required. Entries in the square being costs, times or distances. The assignment method is a special linear programming technique for solving problems like choosing the right man for the right job when more than one choice is possible and when each man can perform all of the jobs. The ultimate objective is to assign a number of tasks to an equal number of facilities at minimum cost (or maximum profit) or some other specific goal. Let there be 'm' resources and 'n' activities. Let c ij be the effectiveness (in terms of cost, profit, time, etc.) of assigning resource i to activity j (i = 1, 2, …., m; j = 1, 2,…., n). Let x ij = 0, if resource i is not assigned to activity j and x ij = 1, if resource i is assigned to activity j. Then the objective is to determine x ij 's that will optimize the total effectiveness (Z) satisfying all the resource constraints and activity constraints. 1. Mathematical Formulation Let number of rows = m and number of columns = n. If m = n then an AP is said to be BAP otherwise it is said to be UBAP. A) Case 1: If m < n then mathematically the UBAP can be stated as follows:
Malaya Journal of Matematik
DR ANJU KHANDELWAL
International Journal for Research in Applied Science & Engineering Technology (IJRASET)
IJRASET Publication
In this paper a new method is proposed for finding an optimal solution of a wide range of assignment problems, directly. A numerical illustration is established and the optimality of the result yielded by this method is also checked. The most attractive feature of this method is that it requires very simple arithmetical and logical calculations. The method is illustrated through an example.
Hussein Ali Hussein Al-Dallal Al-Saeedi
archana pandey
Assignment problems arise in different situation where we have to find an optimal way to assign n-objects to mother objects in an injective fashion. The assignment problems are a well studied topic in combinatorial optimization. These problems find numerous application in production planning, telecommunication VLSI design, economic etc. The assignment problems is a special case of Transportation problem. Depending on the objective we want to optimize, we obtain the typical assignment problems. Assignment problem is an important subject discussed in real physical world we endeavor in this paper to introduce a new approach to assignment problem namely, matrix ones assignment method or MOA-method for solving wide range of problem. An example using matrix ones assignment methods and the existing Hungarian method have been solved and compared it graphically. Also some of the variations and some special cases in assignment problem and its applications have been discussed in the paper.
Sultana Rafi
The assignment problem is a particular type of linear programming problem. In this paper, we analyzed the standard and existing proposed methods. After studying these methods, we proposed a new alternative method for solving the assignment problem. We examined the newly proposed method by a couple of numerical examples and compare this result with the standard method. The main characteristic of this newly proposed method is that it constructed a very easy logical and arithmetical algorithm. Here we point out some advantages and limitations of the new proposed method. Programming code for the newly proposed method has been added in this paper.
Ranjan Kumar Mondal
Thecloudcomputingpresentsatypeofassignmentsandsystemswhichoccupydistributedresources toexecutearoleinadistributedway.Cloudcomputingmakeuseoftheonlinesystemsonthewebto assisttheimplementationofcomplicatedassignments;thatneedhuge-scalecomputation.Itwassaid withtheintentionofinourlivingworld;wecanfinditchallengingtobalanceworkloadsofcloud computingamongassignments(jobsortasks)andsystems(machinesornodes),sothemajorityofthe timewehavetopromoteaconditiontounbalancedassignmentproblems(unequaltaskallocations). The present article submits a new technique to solve the unequal task allocation problems. The techniqueisofferedinanalgorithmicmodelandputintopracticeontheseveralgroupsofinputto investigatethepresentationandusefulnessoftheworks.Anevaluationispreparedwiththepresented approach.Itmakessurethattheproposedapproachprovidesabetteroutcomebycomparingwith someotherexistingalgorithms.
Industrial Engineering Journal
Shridhar Mhalsekar
Journal of Advances in Mathematics and Computer Science
Hudu Mohammed
Assignment problem is an important area in Operation Research and is also discussed in real physical world. In this paper an attempt has been made to solve the assignment problem using a new Method called the Penalty method. We discuss a numerical example by using the new Method and compare it with standard existing method which is the Hungarian method. We compare the optimal solution of the new Method and the Hungarian method. The new method is a simple procedure, easy to apply for solving assignment problem.
Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
RELATED PAPERS
Philippe Laborie
Michael Florian
Journal of Mathematics and Informatics
Sophia Porchelvi
IOP Publishing
Ajit Pal Singh
YMER Digital
Kalpana Dahiya
Mr Ebenezer Quayson
Transportation Research Part B: Methodological
Michael Patriksson
Applied Mathematical Sciences
Anwar N Jasim
Trisna Darmawansyah
IOSR Journals
Springer eBooks
Mourad Baiou
Oksana Pichugina
Discrete Applied Mathematics
Kurt Jörnsten
European Journal of Operational Research
American Scientific Research Journal for Engineering, Technology, and Sciences
humayra afroz
Nanda Piersma
RELATED TOPICS
- We're Hiring!
- Help Center
- Find new research papers in:
- Health Sciences
- Earth Sciences
- Cognitive Science
- Mathematics
- Computer Science
- Academia ©2024


















IMAGES
VIDEO
COMMENTS
The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has ...
10 Feb 2019. Whenever the cost matrix of an assignment problem is not a square matrix, that is, whenever the number of sources is not equal to the number of destinations, the assignment problem is called an unbalanced assignment problem. In such problems, dummy rows (or columns) are added in the matrix so as to complete it to form a square matrix.
The assignment problem consists of finding, in a weighted bipartite graph, a matching of a given size, in which the sum of weights of the edges is minimum. If the numbers of agents and tasks are equal, then the problem is called balanced assignment. Otherwise, it is called unbalanced assignment. [1] If the total cost of the assignment for all ...
Most libraries for the assignment problem solve either the balanced or unbalanced version of this problem (see the later section). However, whether balanced or unbalanced, it may still occur that the constraint set is infeasible, meaning that there does not exist a (one-sided) perfect matching.
Unbalanced Assignment problem is an assignment problem where the number of facilities is not equal to the number of jobs. To make unbalanced assignment problem, a balanced one, a dummy facility (s) or a dummy job (s) (as the case may be) is introduced with zero cost or time. Get Quantitative Techniques: Theory and Problems now with the O ...
Example: Unbalanced Assignment Problem. Solution. Since the number of persons is less than the number of jobs, we introduce a dummy person (D) with zero values. The revised assignment problem is given below: Table. Now use the Hungarian method to obtain the optimal solution yourself. Ans. = 20 + 17 + 17 + 0 = 54.
Unbalanced Assignment Problem: Unbalanced Assignment problem is an assignment problem where the number of facilities is not equal to the number of jobs. To make unbalanced assignment problem, a balanced one, a dummy facility(s) or a dummy job(s) (as the case may be) is introduced with zero cost or time. Dummy Job/Facility: ...
unbalanced assignment problems is based on the assumption that some jobs should be assigned to pseudo or dummy machines, but these jobs are left unexecuted by the dummy machines in the Hungarian method. However, it is sometimes impractical in real-world situations. Moreover, Lampang, Boonjing, and Chanvarasuth introduced a new space- ...
The typical textbook solution to the balanced assignment problem is then found using Kuhn's [3] Hungarian method. Problems in which there are more jobs than machines and more than one job can be ...
For unbalanced assignment problem where the number of jobs is more than the number of machines, the existing approaches assign some jobs to a dummy machine which means these jobs are left without ...
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
Unbalanced Assignment Problem. If the cost matrix of an assignment problem is not a square matrix, the assignment problem is called an Unbalanced Assignment Problem. In such a case, add dummy row or dummy column with zero cost in the cost matrix so as to form a square matrix. Then apply the usual assignment method to find the optimal solution.
7. PDF. Recently, Yadaiah and Haragopal published in the American Journal of Operations Research a new approach to solving the unbalanced assignment problem. They also provide a numerical example which they solve with their approach and get a cost of 1550 which they claim is optimum. This approach might be of interest; however, their approach ...
The assignment problems are a well studied topic in combinatorial optimization. These problems find numerous application in production planning, telecommunication VLSI design, economic etc. The assignment problems is a special case of Transportation problem. Depending on the objective we want to optimize, we obtain the typical assignment problems.
4. Unbalanced Assignment Problem. Unbalanced Assignment Problem If number of rows is not equal to number of columns then it is called Unbalanced Assignment Problem. So to solve this problem, we have to add dummy rows or columns with cost 0, to make it a square matrix. ExampleFind Solution of Assignment problem using Hungarian method (MIN case)
Unbalanced assignment problem, Hungarian method, Optimal solution. Introduction The assignment problem is a combinatorial optimization problem in the field of operations research. It is a special case and completely degenerate form of a transportation problem, which occurs when each supply is 1 and
Problem definition: unbalanced assignment problem with multiple jobs. The Unbalanced Assignment Problem deals with processing n tasks to m agents (n and m are integers and different) where each task is exactly affected to only one agent and each agent needs to carry out at least one task (and no more than q tasks). The main objective is to ...
Unbalanced transportation problem is defined as a situation in which supply and demand are not equal. A dummy row or a dummy column is added to this type of problem, depending on the necessity, to make it a balanced problem. The problem can then be addressed in the same way as the balanced problem.
The Assignment Problem (AP) is a fundamental combinatorial optimization problem. It can be formally defined as follows. Given a set n workers, a set of n jobs and a \(n \times n\) cost matrix whose elements are positive representing the assignment of any worker to any job, the AP aims at finding an one-to-one worker-job assignment (i.e., a bipartite perfect matching) that minimizes certain ...
Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
How can I balance the following assignment problem (where machines are to be assigned the jobs in optimal way such that the profit is maximized). Cost matrix is given in the problem. First step is to convert it into minimization problem by subtracting all the entries in the matrix from maximum value in the matrix.
Unit 8: Assignment Problem - Unbalanced. When an assignment problem has more than one solution, then it is Notes (a) Multiple Optimal solution (b) The problem is unbalanced (c) Maximization problem (d) Balanced problem. 8 Unbalanced Assignment Problem. If the given matrix is not a square matrix, the assignment problem is called an unbalanced ...
The Assignment problem can be Balanced or Unbalanced problem.. A Balanced problem means the no. of rows and no. of columns in the problem are equal. E. g. if the problem contains 4 workers and 4 jobs, then it is balanced. Where as, an Unbalanced problem means the no. of rows and no. of columns are not equal.E. g. if the problem contains 4 workers and 3 jobs it is not balanced.