

User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
S.3.2 hypothesis testing (p-value approach).
The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or equal to) \(\alpha\), then it is "unlikely." And, if the P -value is large, say more than \(\alpha\), then it is "likely."
If the P -value is less than (or equal to) \(\alpha\), then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P -value is greater than \(\alpha\), then the null hypothesis is not rejected.
Specifically, the four steps involved in using the P -value approach to conducting any hypothesis test are:
- Specify the null and alternative hypotheses.
- Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
- Using the known distribution of the test statistic, calculate the P -value : "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
- Set the significance level, \(\alpha\), the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P -value to \(\alpha\). If the P -value is less than (or equal to) \(\alpha\), reject the null hypothesis in favor of the alternative hypothesis. If the P -value is greater than \(\alpha\), do not reject the null hypothesis.
Example S.3.2.1
Mean gpa section .
In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * equaling 2.5. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.
Right Tailed
The P -value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t * = 2.5 if the population mean \(\mu\) really were 3. Recall that probability equals the area under the probability curve. The P -value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t * = 2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.
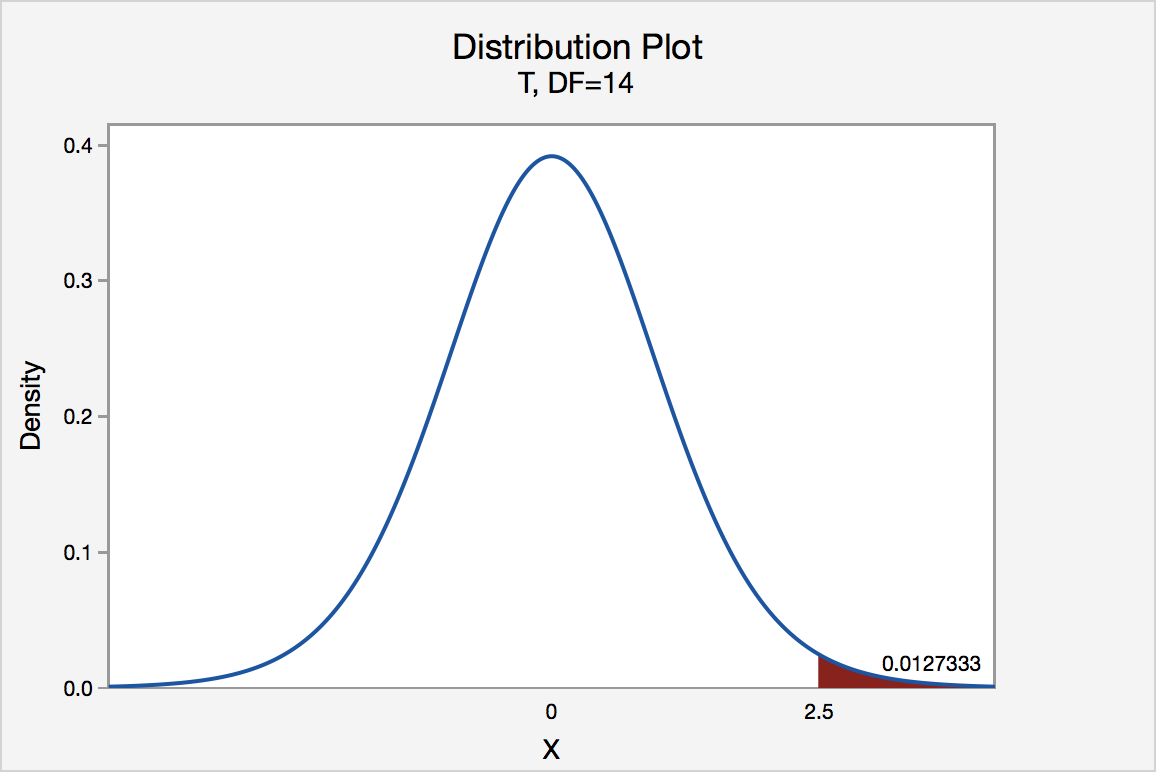
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than \(\alpha\) = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3.
Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to \(\alpha\) = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.
Left Tailed
In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t * = -2.5 if the population mean μ really were 3. The P -value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.
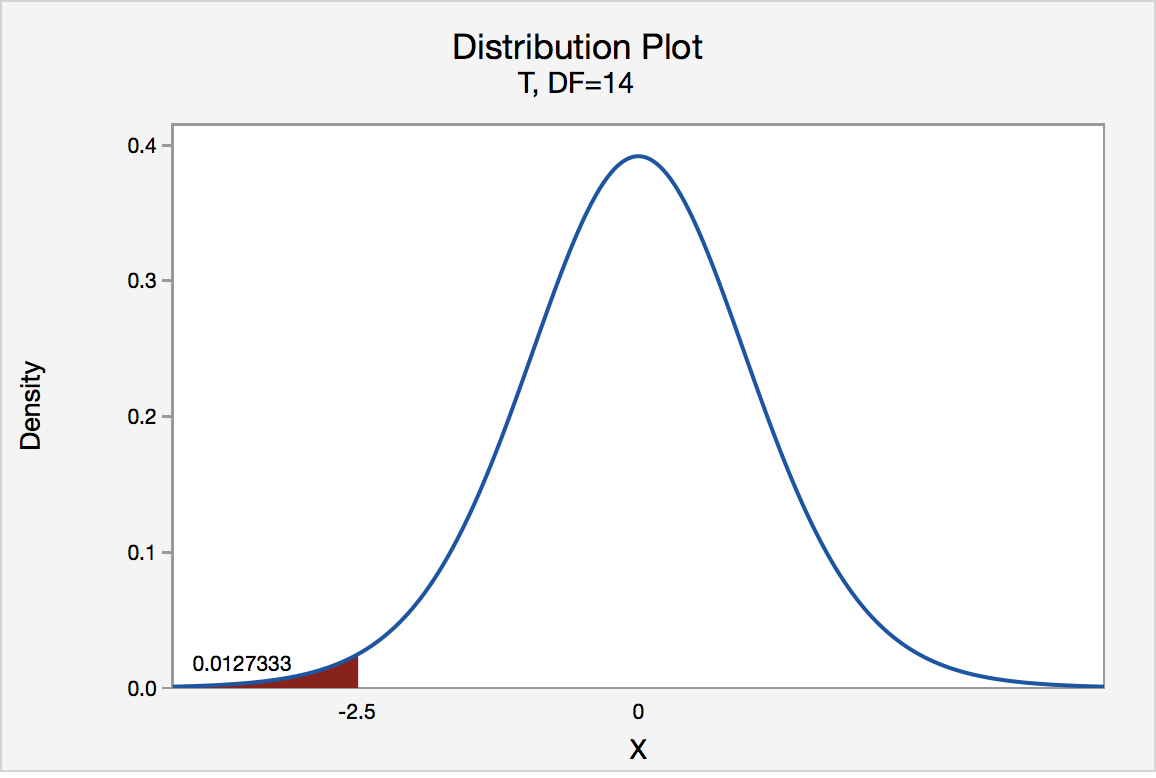
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3.
Note that we would not reject H 0 : μ = 3 in favor of H A : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0127, is then greater than \(\alpha\) = 0.01.
In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P -value is, therefore, the area under a t n - 1 = t 14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P -value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.
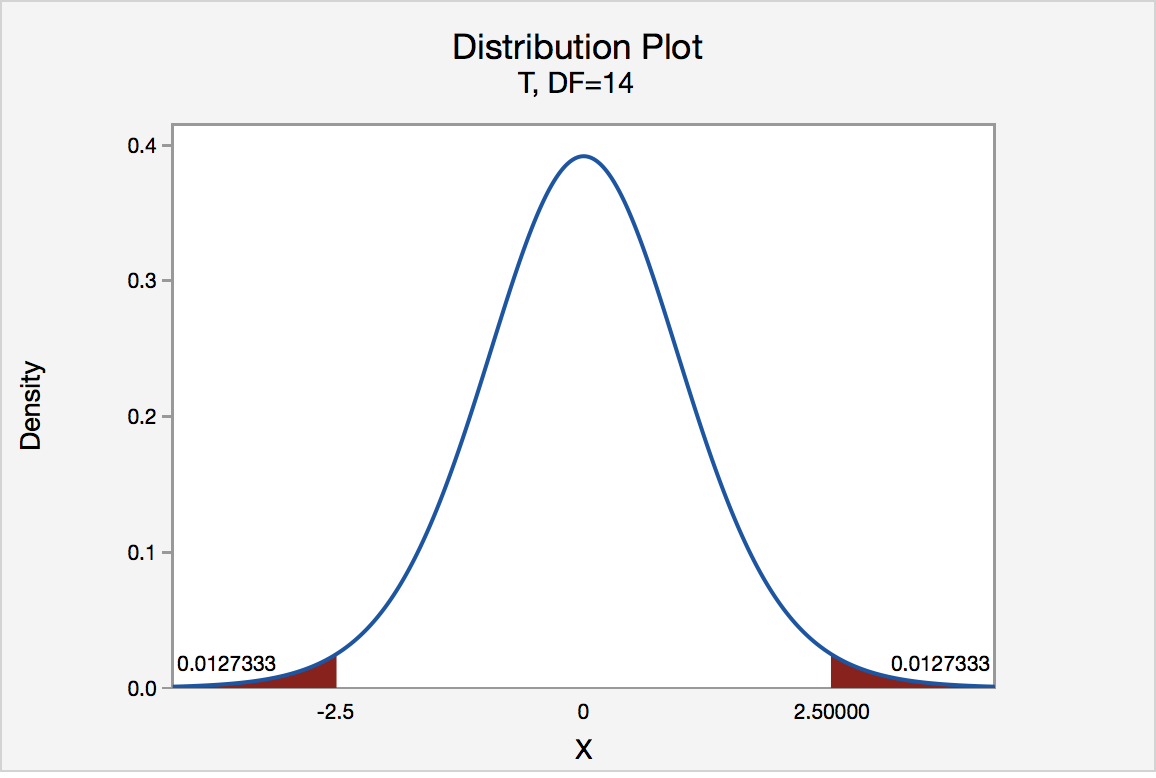
Note that the P -value for a two-tailed test is always two times the P -value for either of the one-tailed tests. The P -value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0254, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3.
Note that we would not reject H 0 : μ = 3 in favor of H A : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0254, is then greater than \(\alpha\) = 0.01.
Now that we have reviewed the critical value and P -value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.
The good news is that, whenever possible, we will take advantage of the test statistics and P -values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.
P-Value in Statistical Hypothesis Tests: What is it?
P value definition.
A p value is used in hypothesis testing to help you support or reject the null hypothesis . The p value is the evidence against a null hypothesis . The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.
P values are expressed as decimals although it may be easier to understand what they are if you convert them to a percentage . For example, a p value of 0.0254 is 2.54%. This means there is a 2.54% chance your results could be random (i.e. happened by chance). That’s pretty tiny. On the other hand, a large p-value of .9(90%) means your results have a 90% probability of being completely random and not due to anything in your experiment. Therefore, the smaller the p-value, the more important (“ significant “) your results.
When you run a hypothesis test , you compare the p value from your test to the alpha level you selected when you ran the test. Alpha levels can also be written as percentages.
P Value vs Alpha level
Alpha levels are controlled by the researcher and are related to confidence levels . You get an alpha level by subtracting your confidence level from 100%. For example, if you want to be 98 percent confident in your research, the alpha level would be 2% (100% – 98%). When you run the hypothesis test, the test will give you a value for p. Compare that value to your chosen alpha level. For example, let’s say you chose an alpha level of 5% (0.05). If the results from the test give you:
- A small p (≤ 0.05), reject the null hypothesis . This is strong evidence that the null hypothesis is invalid.
- A large p (> 0.05) means the alternate hypothesis is weak, so you do not reject the null.
P Values and Critical Values

What if I Don’t Have an Alpha Level?
In an ideal world, you’ll have an alpha level. But if you do not, you can still use the following rough guidelines in deciding whether to support or reject the null hypothesis:
- If p > .10 → “not significant”
- If p ≤ .10 → “marginally significant”
- If p ≤ .05 → “significant”
- If p ≤ .01 → “highly significant.”
How to Calculate a P Value on the TI 83
Example question: The average wait time to see an E.R. doctor is said to be 150 minutes. You think the wait time is actually less. You take a random sample of 30 people and find their average wait is 148 minutes with a standard deviation of 5 minutes. Assume the distribution is normal. Find the p value for this test.
- Press STAT then arrow over to TESTS.
- Press ENTER for Z-Test .
- Arrow over to Stats. Press ENTER.
- Arrow down to μ0 and type 150. This is our null hypothesis mean.
- Arrow down to σ. Type in your std dev: 5.
- Arrow down to xbar. Type in your sample mean : 148.
- Arrow down to n. Type in your sample size : 30.
- Arrow to <μ0 for a left tail test . Press ENTER.
- Arrow down to Calculate. Press ENTER. P is given as .014, or about 1%.
The probability that you would get a sample mean of 148 minutes is tiny, so you should reject the null hypothesis.
Note : If you don’t want to run a test, you could also use the TI 83 NormCDF function to get the area (which is the same thing as the probability value).
Dodge, Y. (2008). The Concise Encyclopedia of Statistics . Springer. Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial.
Warning: The NCBI web site requires JavaScript to function. more...
An official website of the United States government
The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
- Browse Titles
NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.
StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].
Hypothesis testing, p values, confidence intervals, and significance.
Jacob Shreffler ; Martin R. Huecker .
Affiliations
Last Update: March 13, 2023 .
- Definition/Introduction
Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.
- Issues of Concern
Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.
Hypothesis Testing
Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:
Research Question: Is Drug 23 an effective treatment for Disease A?
Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.
Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.
The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.
Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.
Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).
To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1] When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]
Significance
Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3] Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4] When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5] One criterion often used to determine statistical significance is the utilization of p values.
P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6] Hypothesis testing allows us to determine the size of the effect.
An example of findings reported with p values are below:
Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.
Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.
For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7] The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.
While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3] In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]
When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]
Confidence Intervals
A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12] Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13] A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14] Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15] confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]
In consideration of the similar research example provided above, one could make the following statement with 95% CI:
Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).
It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14] A larger width indicates a smaller sample size or a larger variability. [16] A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]
Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15] Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.
Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14] In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13] An example is below:
Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).
- Clinical Significance
Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14] Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.
Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4] Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]
The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.
- Nursing, Allied Health, and Interprofessional Team Interventions
All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care.
- Review Questions
- Access free multiple choice questions on this topic.
- Comment on this article.
Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.
Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.
This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.
- Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.
In this Page
Bulk download.
- Bulk download StatPearls data from FTP
Related information
- PMC PubMed Central citations
- PubMed Links to PubMed
Similar articles in PubMed
- The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). [PeerJ. 2021] The reporting of p values, confidence intervals and statistical significance in Preventive Veterinary Medicine (1997-2017). Messam LLM, Weng HY, Rosenberger NWY, Tan ZH, Payet SDM, Santbakshsing M. PeerJ. 2021; 9:e12453. Epub 2021 Nov 24.
- Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. [J Pharm Pract. 2010] Review Clinical versus statistical significance: interpreting P values and confidence intervals related to measures of association to guide decision making. Ferrill MJ, Brown DA, Kyle JA. J Pharm Pract. 2010 Aug; 23(4):344-51. Epub 2010 Apr 13.
- Interpreting "statistical hypothesis testing" results in clinical research. [J Ayurveda Integr Med. 2012] Interpreting "statistical hypothesis testing" results in clinical research. Sarmukaddam SB. J Ayurveda Integr Med. 2012 Apr; 3(2):65-9.
- Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. [Dermatol Surg. 2005] Confidence intervals in procedural dermatology: an intuitive approach to interpreting data. Alam M, Barzilai DA, Wrone DA. Dermatol Surg. 2005 Apr; 31(4):462-6.
- Review Is statistical significance testing useful in interpreting data? [Reprod Toxicol. 1993] Review Is statistical significance testing useful in interpreting data? Savitz DA. Reprod Toxicol. 1993; 7(2):95-100.
Recent Activity
- Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls
Your browsing activity is empty.
Activity recording is turned off.
Turn recording back on
Connect with NLM
National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894
Web Policies FOIA HHS Vulnerability Disclosure
Help Accessibility Careers
- Data Science
- Data Analysis
- Data Visualization
- Machine Learning
- Deep Learning
- Computer Vision
- Artificial Intelligence
- AI ML DS Interview Series
- AI ML DS Projects series
- Data Engineering
- Web Scrapping
P-Value: Comprehensive Guide to Understand, Apply, and Interpret
A p-value is a statistical metric used to assess a hypothesis by comparing it with observed data.
This article delves into the concept of p-value, its calculation, interpretation, and significance. It also explores the factors that influence p-value and highlights its limitations.
Table of Content
- What is P-value?
How P-value is calculated?
How to interpret p-value, p-value in hypothesis testing, implementing p-value in python, applications of p-value, what is the p-value.
The p-value, or probability value, is a statistical measure used in hypothesis testing to assess the strength of evidence against a null hypothesis. It represents the probability of obtaining results as extreme as, or more extreme than, the observed results under the assumption that the null hypothesis is true.
In simpler words, it is used to reject or support the null hypothesis during hypothesis testing. In data science, it gives valuable insights on the statistical significance of an independent variable in predicting the dependent variable.
Calculating the p-value typically involves the following steps:
- Formulate the Null Hypothesis (H0) : Clearly state the null hypothesis, which typically states that there is no significant relationship or effect between the variables.
- Choose an Alternative Hypothesis (H1) : Define the alternative hypothesis, which proposes the existence of a significant relationship or effect between the variables.
- Determine the Test Statistic : Calculate the test statistic, which is a measure of the discrepancy between the observed data and the expected values under the null hypothesis. The choice of test statistic depends on the type of data and the specific research question.
- Identify the Distribution of the Test Statistic : Determine the appropriate sampling distribution for the test statistic under the null hypothesis. This distribution represents the expected values of the test statistic if the null hypothesis is true.
- Calculate the Critical-value : Based on the observed test statistic and the sampling distribution, find the probability of obtaining the observed test statistic or a more extreme one, assuming the null hypothesis is true.
- Interpret the results: Compare the critical-value with t-statistic. If the t-statistic is larger than the critical value, it provides evidence to reject the null hypothesis, and vice-versa.
Its interpretation depends on the specific test and the context of the analysis. Several popular methods for calculating test statistics that are utilized in p-value calculations.
Test | Scenario | Interpretation |
|---|---|---|
| Used when dealing with large sample sizes or when the population standard deviation is known. | A small p-value (smaller than 0.05) indicates strong evidence against the null hypothesis, leading to its rejection. |
| Appropriate for small sample sizes or when the population standard deviation is unknown. | Similar to the Z-test |
|
| Used for tests of independence or goodness-of-fit. | A small p-value indicates that there is a significant association between the categorical variables, leading to the rejection of the null hypothesis. |
| Commonly used in Analysis of Variance (ANOVA) to compare variances between groups. | A small p-value suggests that at least one group mean is different from the others, leading to the rejection of the null hypothesis. |
| Measures the strength and direction of a linear relationship between two continuous variables. | A small p-value indicates that there is a significant linear relationship between the variables, leading to rejection of the null hypothesis that there is no correlation. |
In general, a small p-value indicates that the observed data is unlikely to have occurred by random chance alone, which leads to the rejection of the null hypothesis. However, it’s crucial to choose the appropriate test based on the nature of the data and the research question, as well as to interpret the p-value in the context of the specific test being used.
The table given below shows the importance of p-value and shows the various kinds of errors that occur during hypothesis testing.
|
|
|
| Correct decision based | Type I error |
| Type II error | Incorrect decision based |
Type I error: Incorrect rejection of the null hypothesis. It is denoted by α (significance level). Type II error: Incorrect acceptance of the null hypothesis. It is denoted by β (power level)
Let’s consider an example to illustrate the process of calculating a p-value for Two Sample T-Test:
A researcher wants to investigate whether there is a significant difference in mean height between males and females in a population of university students.
Suppose we have the following data:
Starting with interpreting the process of calculating p-value
Step 1 : Formulate the Null Hypothesis (H0):
H0: There is no significant difference in mean height between males and females.
Step 2 : Choose an Alternative Hypothesis (H1):
H1: There is a significant difference in mean height between males and females.
Step 3 : Determine the Test Statistic:
The appropriate test statistic for this scenario is the two-sample t-test, which compares the means of two independent groups.
The t-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

- s1 = First sample’s standard deviation
- s2 = Second sample’s standard deviation
- n1 = First sample’s sample size
- n2 = Second sample’s sample size

So, the calculated two-sample t-test statistic (t) is approximately 5.13.
Step 4 : Identify the Distribution of the Test Statistic:
The t-distribution is used for the two-sample t-test . The degrees of freedom for the t-distribution are determined by the sample sizes of the two groups.
The t-distribution is a probability distribution with tails that are thicker than those of the normal distribution.
- where, n1 is total number of values for 1st category.
- n2 is total number of values for 2nd category.
The degrees of freedom (63) represent the variability available in the data to estimate the population parameters. In the context of the two-sample t-test, higher degrees of freedom provide a more precise estimate of the population variance, influencing the shape and characteristics of the t-distribution.
.png)
T-Statistic
The t-distribution is symmetric and bell-shaped, similar to the normal distribution. As the degrees of freedom increase, the t-distribution approaches the shape of the standard normal distribution. Practically, it affects the critical values used to determine statistical significance and confidence intervals.
Step 5 : Calculate Critical Value.
To find the critical t-value with a t-statistic of 5.13 and 63 degrees of freedom, we can either consult a t-table or use statistical software.
We can use scipy.stats module in Python to find the critical t-value using below code.
Comparing with T-Statistic:
The larger t-statistic suggests that the observed difference between the sample means is unlikely to have occurred by random chance alone. Therefore, we reject the null hypothesis.
- p ≤ (α = 0.05) : Reject the null hypothesis. There is sufficient evidence to conclude that the observed effect or relationship is statistically significant, meaning it is unlikely to have occurred by chance alone.
- p > (α = 0.05) : reject alternate hypothesis (or accept null hypothesis). The observed effect or relationship does not provide enough evidence to reject the null hypothesis. This does not necessarily mean there is no effect; it simply means the sample data does not provide strong enough evidence to rule out the possibility that the effect is due to chance.
In case the significance level is not specified, consider the below general inferences while interpreting your results.
- If p > .10: not significant
- If p ≤ .10: slightly significant
- If p ≤ .05: significant
- If p ≤ .001: highly significant
Graphically, the p-value is located at the tails of any confidence interval. [As shown in fig 1]

Fig 1: Graphical Representation
What influences p-value?
The p-value in hypothesis testing is influenced by several factors:
- Sample Size : Larger sample sizes tend to yield smaller p-values, increasing the likelihood of detecting significant effects.
- Effect Size: A larger effect size results in smaller p-values, making it easier to detect a significant relationship.
- Variability in the Data : Greater variability often leads to larger p-values, making it harder to identify significant effects.
- Significance Level : A lower chosen significance level increases the threshold for considering p-values as significant.
- Choice of Test: Different statistical tests may yield different p-values for the same data.
- Assumptions of the Test : Violations of test assumptions can impact p-values.
Understanding these factors is crucial for interpreting p-values accurately and making informed decisions in hypothesis testing.
Significance of P-value
- The p-value provides a quantitative measure of the strength of the evidence against the null hypothesis.
- Decision-Making in Hypothesis Testing
- P-value serves as a guide for interpreting the results of a statistical test. A small p-value suggests that the observed effect or relationship is statistically significant, but it does not necessarily mean that it is practically or clinically meaningful.
Limitations of P-value
- The p-value is not a direct measure of the effect size, which represents the magnitude of the observed relationship or difference between variables. A small p-value does not necessarily mean that the effect size is large or practically meaningful.
- Influenced by Various Factors
The p-value is a crucial concept in statistical hypothesis testing, serving as a guide for making decisions about the significance of the observed relationship or effect between variables.
Let’s consider a scenario where a tutor believes that the average exam score of their students is equal to the national average (85). The tutor collects a sample of exam scores from their students and performs a one-sample t-test to compare it to the population mean (85).
- The code performs a one-sample t-test to compare the mean of a sample data set to a hypothesized population mean.
- It utilizes the scipy.stats library to calculate the t-statistic and p-value. SciPy is a Python library that provides efficient numerical routines for scientific computing.
- The p-value is compared to a significance level (alpha) to determine whether to reject the null hypothesis.
Since, 0.7059>0.05 , we would conclude to fail to reject the null hypothesis. This means that, based on the sample data, there isn’t enough evidence to claim a significant difference in the exam scores of the tutor’s students compared to the national average. The tutor would accept the null hypothesis, suggesting that the average exam score of their students is statistically consistent with the national average.
- During Forward and Backward propagation: When fitting a model (say a Multiple Linear Regression model), we use the p-value in order to find the most significant variables that contribute significantly in predicting the output.
- Effects of various drug medicines: It is highly used in the field of medical research in determining whether the constituents of any drug will have the desired effect on humans or not. P-value is a very strong statistical tool used in hypothesis testing. It provides a plethora of valuable information while making an important decision like making a business intelligence inference or determining whether a drug should be used on humans or not, etc. For any doubt/query, comment below.
The p-value is a crucial concept in statistical hypothesis testing, providing a quantitative measure of the strength of evidence against the null hypothesis. It guides decision-making by comparing the p-value to a chosen significance level, typically 0.05. A small p-value indicates strong evidence against the null hypothesis, suggesting a statistically significant relationship or effect. However, the p-value is influenced by various factors and should be interpreted alongside other considerations, such as effect size and context.
Frequently Based Questions (FAQs)
Why is p-value greater than 1.
A p-value is a probability, and probabilities must be between 0 and 1. Therefore, a p-value greater than 1 is not possible.
What does P 0.01 mean?
It means that the observed test statistic is unlikely to occur by chance if the null hypothesis is true. It represents a 1% chance of observing the test statistic or a more extreme one under the null hypothesis.
Is 0.9 a good p-value?
A good p-value is typically less than or equal to 0.05, indicating that the null hypothesis is likely false and the observed relationship or effect is statistically significant.
What is p-value in a model?
It is a measure of the statistical significance of a parameter in the model. It represents the probability of obtaining the observed value of the parameter or a more extreme one, assuming the null hypothesis is true.
Why is p-value so low?
A low p-value means that the observed test statistic is unlikely to occur by chance if the null hypothesis is true. It suggests that the observed relationship or effect is statistically significant and not due to random sampling variation.
How Can You Use P-value to Compare Two Different Results of a Hypothesis Test?
Compare p-values: Lower p-value indicates stronger evidence against null hypothesis, favoring results with smaller p-values in hypothesis testing.
Similar Reads
Please login to comment....
- Free Music Recording Software in 2024: Top Picks for Windows, Mac, and Linux
- Best Free Music Maker Software in 2024
- What is Quantum AI? The Future of Computing and Artificial Intelligence Explained
- Noel Tata: Ratan Tata's Brother Named as a new Chairman of Tata Trusts
- GeeksforGeeks Practice - Leading Online Coding Platform
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
What is The Null Hypothesis & When Do You Reject The Null Hypothesis
Julia Simkus
Editor at Simply Psychology
BA (Hons) Psychology, Princeton University
Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.
Learn about our Editorial Process
Saul McLeod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.
The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).
The null hypothesis is the statement that a researcher or an investigator wants to disprove.
Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.
How to Write a Null Hypothesis
Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.
It is a default position that your research aims to challenge or confirm.
For example, if studying the impact of exercise on weight loss, your null hypothesis might be:
There is no significant difference in weight loss between individuals who exercise daily and those who do not.
Examples of Null Hypotheses
| Research Question | Null Hypothesis |
|---|---|
| Do teenagers use cell phones more than adults? | Teenagers and adults use cell phones the same amount. |
| Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil? | Tomato plants show no difference in growth rates when planted in compost rather than soil. |
| Does daily meditation decrease the incidence of depression? | Daily meditation does not decrease the incidence of depression. |
| Does daily exercise increase test performance? | There is no relationship between daily exercise time and test performance. |
| Does the new vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does flossing your teeth affect the number of cavities? | Flossing your teeth has no effect on the number of cavities. |
When Do We Reject The Null Hypothesis?
We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.
If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.
Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).
If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.
You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.
Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.
The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.
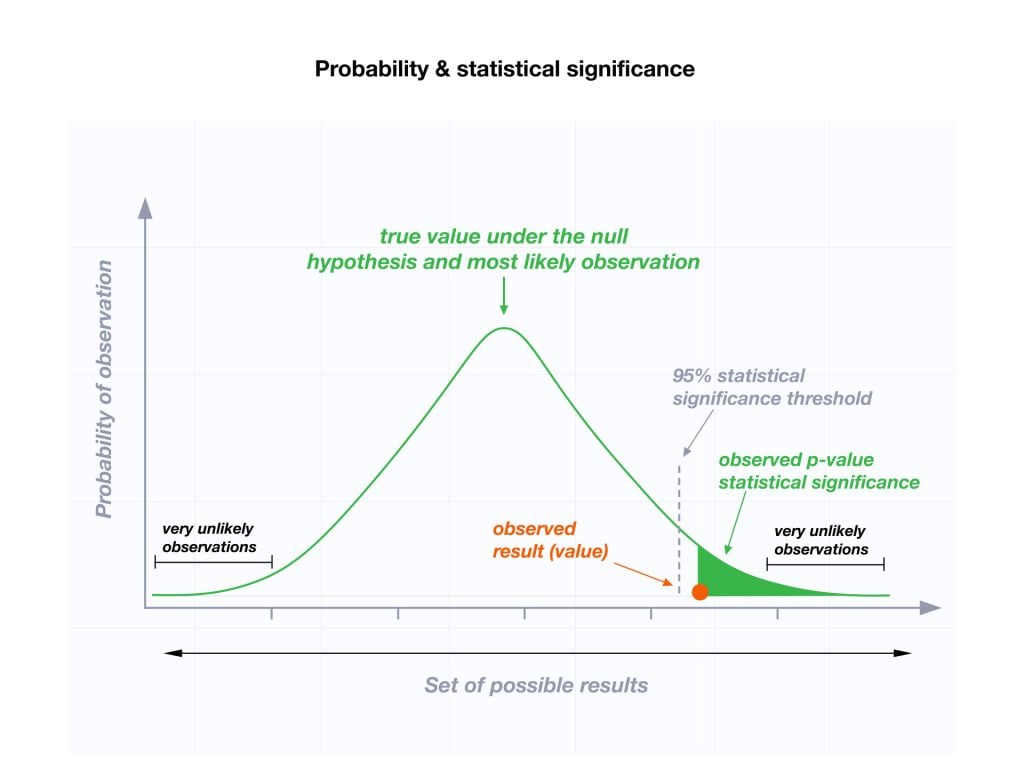
Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.
When your p-value is less than or equal to your significance level, you reject the null hypothesis.
In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.
In this case, the sample data provides insufficient data to conclude that the effect exists in the population.
Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.
When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.
Why Do We Never Accept The Null Hypothesis?
The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.
A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.
It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.
One can either reject the null hypothesis, or fail to reject it, but can never accept it.
Why Do We Use The Null Hypothesis?
We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.
The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).
A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.
Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.
Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.
It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.
Purpose of a Null Hypothesis
- The primary purpose of the null hypothesis is to disprove an assumption.
- Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
- A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.
Do you always need both a Null Hypothesis and an Alternative Hypothesis?
The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.
While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.
The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.
What is the difference between a null hypothesis and an alternative hypothesis?
The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.
It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.
What are some problems with the null hypothesis?
One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.
Why can a null hypothesis not be accepted?
We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.
We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.
Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.
If the p-value is greater than the significance level, then you fail to reject the null hypothesis.
Is a null hypothesis directional or non-directional?
A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.
A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.
A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.
The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.
Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.
Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.
Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.
Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.
Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.
p-value Calculator
Table of contents
Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.
P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!
🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.
What is p-value?
Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !
More intuitively, p-value answers the question:
Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?
It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:
Left-tailed test: p-value = Pr(S ≤ x | H 0 )
Right-tailed test: p-value = Pr(S ≥ x | H 0 )
Two-tailed test:
p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}
(By min{a,b} , we denote the smaller number out of a and b .)
If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )
or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )
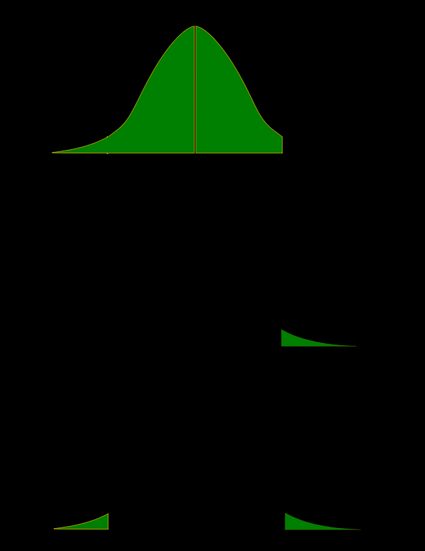
As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.
- Symmetric case: normal distribution:
- Non-symmetric case: chi-squared distribution:
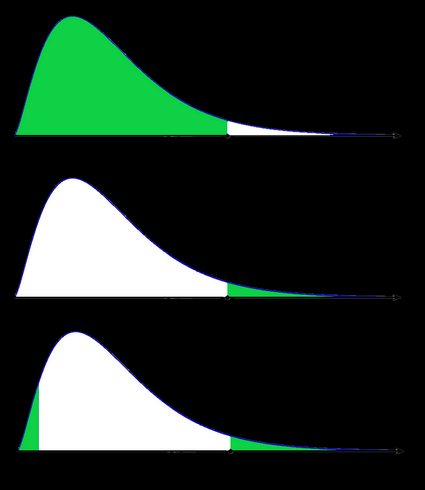
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.
How do I calculate p-value from test statistic?
To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:
Left-tailed test:
p-value = cdf(x) .
Right-tailed test:
p-value = 1 - cdf(x) .
p-value = 2 × min{cdf(x) , 1 - cdf(x)} .
If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .
The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.
Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.
How to interpret p-value
As we have mentioned above, the p-value is the answer to the following question:
What does that mean for you? Well, you've got two options:
- A high p-value means that your data is highly compatible with the null hypothesis; and
- A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.
However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!
The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :
- If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
- If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.
Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.
Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.
How to use the p-value calculator to find p-value from test statistic
As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:
Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.
Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.
If needed, specify the degrees of freedom of the test statistic's distribution.
Enter the value of test statistic computed for your data sample.
By default, the calculator uses the significance level of 0.05.
Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis.
How do I find p-value from z-score?
In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:
Left-tailed z-test:
p-value = Φ(Z score )
Right-tailed z-test:
p-value = 1 - Φ(Z score )
Two-tailed z-test:
p-value = 2 × Φ(−|Z score |)
p-value = 2 - 2 × Φ(|Z score |)
🙋 To learn more about Z-tests, head to Omni's Z-test calculator .
We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.
A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.
How do I find p-value from t?
The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:
Left-tailed t-test:
p-value = cdf t,d (t score )
Right-tailed t-test:
p-value = 1 - cdf t,d (t score )
Two-tailed t-test:
p-value = 2 × cdf t,d (−|t score |)
p-value = 2 - 2 × cdf t,d (|t score |)
Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).
The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .
🙋 To get more insights into t-statistics, we recommend using our t-test calculator .
p-value from chi-square score (χ² score)
Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .
This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!
How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:
Left-tailed χ²-test:
p-value = cdf χ²,d (χ² score )
Right-tailed χ²-test:
p-value = 1 - cdf χ²,d (χ² score )
Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)
Two-tailed χ²-test:
p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}
(By min{a,b} , we denote the smaller of the numbers a and b .)
The most popular tests which lead to a χ²-score are the following:
Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .
Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .
Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

p-value from F-score
Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .
To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .
The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:
Left-tailed F-test:
p-value = cdf F,d1,d2 (F score )
Right-tailed F-test:
p-value = 1 - cdf F,d1,d2 (F score )
Two-tailed F-test:
p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}
Below we list the most important tests that produce F-scores. All of them are right-tailed tests .
A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.
ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).
A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).
With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .
A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.
You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).
Can p-value be negative?
No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.
What does a high p-value mean?
A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.
What does a low p-value mean?
A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.
What do you want?
What do you know?
Your Z-score
Z-score : the test statistic follows the standard normal distribution N(0,1).
.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-63uqft{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-63uqft code,.css-63uqft kbd,.css-63uqft pre,.css-63uqft samp{font-family:monospace;}.css-63uqft code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-63uqft figcaption,.css-63uqft caption{text-align:center;}.css-63uqft figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-63uqft h3{font-size:1.75rem;}.css-63uqft h4{font-size:1.5rem;}.css-63uqft .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-63uqft .mathBlock .katex{font-size:24px;text-align:left;}.css-63uqft .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-63uqft .videoBlock,.css-63uqft .imageBlock{margin-bottom:16px;}.css-63uqft .imageBlock__image-align--left,.css-63uqft .videoBlock__video-align--left{float:left;}.css-63uqft .imageBlock__image-align--right,.css-63uqft .videoBlock__video-align--right{float:right;}.css-63uqft .imageBlock__image-align--center,.css-63uqft .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-63uqft .imageBlock__image-align--none,.css-63uqft .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-63uqft .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-63uqft .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-63uqft .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-63uqft .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-63uqft .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-63uqft .katex .katex-version::after{content:'0.13.13';}.css-63uqft .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-63uqft .katex .katex-html>.newline{display:block;}.css-63uqft .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-63uqft .katex .strut{display:inline-block;}.css-63uqft .katex .textbf{font-weight:bold;}.css-63uqft .katex .textit{font-style:italic;}.css-63uqft .katex .textrm{font-family:KaTeX_Main;}.css-63uqft .katex .textsf{font-family:KaTeX_SansSerif;}.css-63uqft .katex .texttt{font-family:KaTeX_Typewriter;}.css-63uqft .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-63uqft .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-63uqft .katex .mathrm{font-style:normal;}.css-63uqft .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-63uqft .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-63uqft .katex .amsrm{font-family:KaTeX_AMS;}.css-63uqft .katex .mathbb,.css-63uqft .katex .textbb{font-family:KaTeX_AMS;}.css-63uqft .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-63uqft .katex .mathfrak,.css-63uqft .katex .textfrak{font-family:KaTeX_Fraktur;}.css-63uqft .katex .mathtt{font-family:KaTeX_Typewriter;}.css-63uqft .katex .mathscr,.css-63uqft .katex .textscr{font-family:KaTeX_Script;}.css-63uqft .katex .mathsf,.css-63uqft .katex .textsf{font-family:KaTeX_SansSerif;}.css-63uqft .katex .mathboldsf,.css-63uqft .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-63uqft .katex .mathitsf,.css-63uqft .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-63uqft .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-63uqft .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-63uqft .katex .vlist-r{display:table-row;}.css-63uqft .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-63uqft .katex .vlist>span{display:block;height:0;position:relative;}.css-63uqft .katex .vlist>span>span{display:inline-block;}.css-63uqft .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-63uqft .katex .vlist-t2{margin-right:-2px;}.css-63uqft .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-63uqft .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-63uqft .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-63uqft .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-63uqft .katex .msupsub{text-align:left;}.css-63uqft .katex .mfrac>span>span{text-align:center;}.css-63uqft .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-63uqft .katex .mfrac .frac-line,.css-63uqft .katex .overline .overline-line,.css-63uqft .katex .underline .underline-line,.css-63uqft .katex .hline,.css-63uqft .katex .hdashline,.css-63uqft .katex .rule{min-height:1px;}.css-63uqft .katex .mspace{display:inline-block;}.css-63uqft .katex .llap,.css-63uqft .katex .rlap,.css-63uqft .katex .clap{width:0;position:relative;}.css-63uqft .katex .llap>.inner,.css-63uqft .katex .rlap>.inner,.css-63uqft .katex .clap>.inner{position:absolute;}.css-63uqft .katex .llap>.fix,.css-63uqft .katex .rlap>.fix,.css-63uqft .katex .clap>.fix{display:inline-block;}.css-63uqft .katex .llap>.inner{right:0;}.css-63uqft .katex .rlap>.inner,.css-63uqft .katex .clap>.inner{left:0;}.css-63uqft .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-63uqft .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-63uqft .katex .overline .overline-line,.css-63uqft .katex .underline .underline-line,.css-63uqft .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-63uqft .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-63uqft .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-63uqft .katex .sizing.reset-size1.size1,.css-63uqft .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-63uqft .katex .sizing.reset-size1.size2,.css-63uqft .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size1.size3,.css-63uqft .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-63uqft .katex .sizing.reset-size1.size4,.css-63uqft .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-63uqft .katex .sizing.reset-size1.size5,.css-63uqft .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-63uqft .katex .sizing.reset-size1.size6,.css-63uqft .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-63uqft .katex .sizing.reset-size1.size7,.css-63uqft .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-63uqft .katex .sizing.reset-size1.size8,.css-63uqft .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-63uqft .katex .sizing.reset-size1.size9,.css-63uqft .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-63uqft .katex .sizing.reset-size1.size10,.css-63uqft .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-63uqft .katex .sizing.reset-size1.size11,.css-63uqft .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-63uqft .katex .sizing.reset-size2.size1,.css-63uqft .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size2.size2,.css-63uqft .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-63uqft .katex .sizing.reset-size2.size3,.css-63uqft .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-63uqft .katex .sizing.reset-size2.size4,.css-63uqft .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-63uqft .katex .sizing.reset-size2.size5,.css-63uqft .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-63uqft .katex .sizing.reset-size2.size6,.css-63uqft .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-63uqft .katex .sizing.reset-size2.size7,.css-63uqft .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-63uqft .katex .sizing.reset-size2.size8,.css-63uqft .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-63uqft .katex .sizing.reset-size2.size9,.css-63uqft .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-63uqft .katex .sizing.reset-size2.size10,.css-63uqft .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-63uqft .katex .sizing.reset-size2.size11,.css-63uqft .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-63uqft .katex .sizing.reset-size3.size1,.css-63uqft .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-63uqft .katex .sizing.reset-size3.size2,.css-63uqft .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-63uqft .katex .sizing.reset-size3.size3,.css-63uqft .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-63uqft .katex .sizing.reset-size3.size4,.css-63uqft .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-63uqft .katex .sizing.reset-size3.size5,.css-63uqft .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-63uqft .katex .sizing.reset-size3.size6,.css-63uqft .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-63uqft .katex .sizing.reset-size3.size7,.css-63uqft .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-63uqft .katex .sizing.reset-size3.size8,.css-63uqft .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-63uqft .katex .sizing.reset-size3.size9,.css-63uqft .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-63uqft .katex .sizing.reset-size3.size10,.css-63uqft .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-63uqft .katex .sizing.reset-size3.size11,.css-63uqft .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-63uqft .katex .sizing.reset-size4.size1,.css-63uqft .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-63uqft .katex .sizing.reset-size4.size2,.css-63uqft .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-63uqft .katex .sizing.reset-size4.size3,.css-63uqft .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-63uqft .katex .sizing.reset-size4.size4,.css-63uqft .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-63uqft .katex .sizing.reset-size4.size5,.css-63uqft .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-63uqft .katex .sizing.reset-size4.size6,.css-63uqft .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-63uqft .katex .sizing.reset-size4.size7,.css-63uqft .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-63uqft .katex .sizing.reset-size4.size8,.css-63uqft .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-63uqft .katex .sizing.reset-size4.size9,.css-63uqft .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-63uqft .katex .sizing.reset-size4.size10,.css-63uqft .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-63uqft .katex .sizing.reset-size4.size11,.css-63uqft .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-63uqft .katex .sizing.reset-size5.size1,.css-63uqft .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-63uqft .katex .sizing.reset-size5.size2,.css-63uqft .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-63uqft .katex .sizing.reset-size5.size3,.css-63uqft .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-63uqft .katex .sizing.reset-size5.size4,.css-63uqft .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-63uqft .katex .sizing.reset-size5.size5,.css-63uqft .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-63uqft .katex .sizing.reset-size5.size6,.css-63uqft .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-63uqft .katex .sizing.reset-size5.size7,.css-63uqft .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-63uqft .katex .sizing.reset-size5.size8,.css-63uqft .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-63uqft .katex .sizing.reset-size5.size9,.css-63uqft .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-63uqft .katex .sizing.reset-size5.size10,.css-63uqft .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-63uqft .katex .sizing.reset-size5.size11,.css-63uqft .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-63uqft .katex .sizing.reset-size6.size1,.css-63uqft .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-63uqft .katex .sizing.reset-size6.size2,.css-63uqft .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-63uqft .katex .sizing.reset-size6.size3,.css-63uqft .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-63uqft .katex .sizing.reset-size6.size4,.css-63uqft .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-63uqft .katex .sizing.reset-size6.size5,.css-63uqft .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-63uqft .katex .sizing.reset-size6.size6,.css-63uqft .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-63uqft .katex .sizing.reset-size6.size7,.css-63uqft .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size6.size8,.css-63uqft .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-63uqft .katex .sizing.reset-size6.size9,.css-63uqft .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-63uqft .katex .sizing.reset-size6.size10,.css-63uqft .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-63uqft .katex .sizing.reset-size6.size11,.css-63uqft .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-63uqft .katex .sizing.reset-size7.size1,.css-63uqft .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-63uqft .katex .sizing.reset-size7.size2,.css-63uqft .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-63uqft .katex .sizing.reset-size7.size3,.css-63uqft .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-63uqft .katex .sizing.reset-size7.size4,.css-63uqft .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-63uqft .katex .sizing.reset-size7.size5,.css-63uqft .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-63uqft .katex .sizing.reset-size7.size6,.css-63uqft .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size7.size7,.css-63uqft .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-63uqft .katex .sizing.reset-size7.size8,.css-63uqft .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size7.size9,.css-63uqft .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-63uqft .katex .sizing.reset-size7.size10,.css-63uqft .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-63uqft .katex .sizing.reset-size7.size11,.css-63uqft .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-63uqft .katex .sizing.reset-size8.size1,.css-63uqft .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-63uqft .katex .sizing.reset-size8.size2,.css-63uqft .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-63uqft .katex .sizing.reset-size8.size3,.css-63uqft .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-63uqft .katex .sizing.reset-size8.size4,.css-63uqft .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-63uqft .katex .sizing.reset-size8.size5,.css-63uqft .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-63uqft .katex .sizing.reset-size8.size6,.css-63uqft .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-63uqft .katex .sizing.reset-size8.size7,.css-63uqft .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size8.size8,.css-63uqft .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-63uqft .katex .sizing.reset-size8.size9,.css-63uqft .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size8.size10,.css-63uqft .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-63uqft .katex .sizing.reset-size8.size11,.css-63uqft .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-63uqft .katex .sizing.reset-size9.size1,.css-63uqft .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-63uqft .katex .sizing.reset-size9.size2,.css-63uqft .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-63uqft .katex .sizing.reset-size9.size3,.css-63uqft .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-63uqft .katex .sizing.reset-size9.size4,.css-63uqft .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-63uqft .katex .sizing.reset-size9.size5,.css-63uqft .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-63uqft .katex .sizing.reset-size9.size6,.css-63uqft .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-63uqft .katex .sizing.reset-size9.size7,.css-63uqft .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-63uqft .katex .sizing.reset-size9.size8,.css-63uqft .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size9.size9,.css-63uqft .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-63uqft .katex .sizing.reset-size9.size10,.css-63uqft .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-63uqft .katex .sizing.reset-size9.size11,.css-63uqft .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-63uqft .katex .sizing.reset-size10.size1,.css-63uqft .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-63uqft .katex .sizing.reset-size10.size2,.css-63uqft .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-63uqft .katex .sizing.reset-size10.size3,.css-63uqft .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-63uqft .katex .sizing.reset-size10.size4,.css-63uqft .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-63uqft .katex .sizing.reset-size10.size5,.css-63uqft .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-63uqft .katex .sizing.reset-size10.size6,.css-63uqft .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-63uqft .katex .sizing.reset-size10.size7,.css-63uqft .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-63uqft .katex .sizing.reset-size10.size8,.css-63uqft .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-63uqft .katex .sizing.reset-size10.size9,.css-63uqft .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-63uqft .katex .sizing.reset-size10.size10,.css-63uqft .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-63uqft .katex .sizing.reset-size10.size11,.css-63uqft .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-63uqft .katex .sizing.reset-size11.size1,.css-63uqft .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-63uqft .katex .sizing.reset-size11.size2,.css-63uqft .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-63uqft .katex .sizing.reset-size11.size3,.css-63uqft .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-63uqft .katex .sizing.reset-size11.size4,.css-63uqft .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-63uqft .katex .sizing.reset-size11.size5,.css-63uqft .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-63uqft .katex .sizing.reset-size11.size6,.css-63uqft .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-63uqft .katex .sizing.reset-size11.size7,.css-63uqft .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-63uqft .katex .sizing.reset-size11.size8,.css-63uqft .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-63uqft .katex .sizing.reset-size11.size9,.css-63uqft .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-63uqft .katex .sizing.reset-size11.size10,.css-63uqft .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-63uqft .katex .sizing.reset-size11.size11,.css-63uqft .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-63uqft .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-63uqft .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-63uqft .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-63uqft .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-63uqft .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-63uqft .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-63uqft .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-63uqft .katex .delimcenter{position:relative;}.css-63uqft .katex .op-symbol{position:relative;}.css-63uqft .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-63uqft .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-63uqft .katex .op-limits>.vlist-t{text-align:center;}.css-63uqft .katex .accent>.vlist-t{text-align:center;}.css-63uqft .katex .accent .accent-body{position:relative;}.css-63uqft .katex .accent .accent-body:not(.accent-full){width:0;}.css-63uqft .katex .overlay{display:block;}.css-63uqft .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-63uqft .katex .mtable .arraycolsep{display:inline-block;}.css-63uqft .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-63uqft .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-63uqft .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-63uqft .katex .svg-align{text-align:left;}.css-63uqft .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-63uqft .katex svg path{stroke:none;}.css-63uqft .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-63uqft .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-63uqft .katex .stretchy::before,.css-63uqft .katex .stretchy::after{content:'';}.css-63uqft .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-63uqft .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-63uqft .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-63uqft .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-63uqft .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-63uqft .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-63uqft .katex .x-arrow-pad{padding:0 0.5em;}.css-63uqft .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-63uqft .katex .x-arrow,.css-63uqft .katex .mover,.css-63uqft .katex .munder{text-align:center;}.css-63uqft .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-63uqft .katex .fbox,.css-63uqft .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-63uqft .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-63uqft .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-63uqft .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-63uqft .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-63uqft .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-63uqft .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-63uqft .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-63uqft .katex .mtr-glue{width:50%;}.css-63uqft .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-63uqft .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-63uqft .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-63uqft .katex-display{display:block;margin:1em 0;text-align:center;}.css-63uqft .katex-display>.katex{display:block;white-space:nowrap;}.css-63uqft .katex-display>.katex>.katex-html{display:block;position:relative;}.css-63uqft .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-63uqft .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-63uqft .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-63uqft body{counter-reset:katexEqnNo mmlEqnNo;}.css-63uqft table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-63uqft .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-63uqft .tableBlock thead,.css-63uqft .tableBlock thead th{border-bottom:1px solid #333!important;}.css-63uqft .tableBlock th,.css-63uqft .tableBlock td{padding:10px;text-align:left;}.css-63uqft .tableBlock th{font-weight:bold!important;}.css-63uqft .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-63uqft .tableBlock caption>p{margin:0;}.css-63uqft .tableBlock th>p,.css-63uqft .tableBlock td>p{margin:0;}.css-63uqft .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-63uqft .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-63uqft .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-63uqft .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-63uqft .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-63uqft .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-63uqft .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-63uqft .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-63uqft .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-63uqft .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-63uqft .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-63uqft .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-63uqft .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-63uqft .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-63uqft .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-63uqft .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-63uqft .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-63uqft .tableBlock [data-text-align='center']{text-align:center;}.css-63uqft .tableBlock [data-text-align='left']{text-align:left;}.css-63uqft .tableBlock [data-text-align='right']{text-align:right;}.css-63uqft .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-63uqft .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-63uqft .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-63uqft .tableBlock__font-size--xxsmall{font-size:10px;}.css-63uqft .tableBlock__font-size--xsmall{font-size:12px;}.css-63uqft .tableBlock__font-size--small{font-size:14px;}.css-63uqft .tableBlock__font-size--large{font-size:18px;}.css-63uqft .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-63uqft .tableBlock__border--bordered td,.css-63uqft .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-63uqft .tableBlock__border--borderless tbody+tbody,.css-63uqft .tableBlock__border--borderless td,.css-63uqft .tableBlock__border--borderless th,.css-63uqft .tableBlock__border--borderless tr,.css-63uqft .tableBlock__border--borderless thead,.css-63uqft .tableBlock__border--borderless thead th{border:0!important;}.css-63uqft .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-63uqft .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-63uqft .tableBlock__table-compactl th,.css-63uqft .tableBlock__table-compact td{padding:3px!important;}.css-63uqft .tableBlock__full-size{width:100%;}.css-63uqft .textBlock{margin-bottom:16px;}.css-63uqft .textBlock__text-formatting--finePrint{font-size:12px;}.css-63uqft .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-63uqft .textBlock__text-infoBox p{margin:0;}.css-63uqft .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-63uqft .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-63uqft .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-63uqft .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-63uqft .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-63uqft .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-63uqft .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-63uqft .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-63uqft.css-63uqft{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-63uqft.css-63uqft:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-63uqft .js-external-link-button.link-like,.css-63uqft .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-63uqft .js-external-link-button.link-like:hover,.css-63uqft .js-external-link-anchor:hover,.css-63uqft .js-external-link-button.link-like:active,.css-63uqft .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-63uqft .js-external-link-button.link-like:focus-visible,.css-63uqft .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-63uqft p,.css-63uqft div{margin:0;display:block;}.css-63uqft pre{margin:0;display:block;}.css-63uqft pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-63uqft pre:not(:first-child){padding-top:8px;}.css-63uqft ul,.css-63uqft ol{display:block margin:0;padding-left:20px;}.css-63uqft ul li,.css-63uqft ol li{padding-top:8px;}.css-63uqft ul ul,.css-63uqft ol ul,.css-63uqft ul ol,.css-63uqft ol ol{padding-top:0;}.css-63uqft ul:not(:first-child),.css-63uqft ol:not(:first-child){padding-top:4px;} Interpretation
Significance level α
The Data Scientist

Understanding Critical Value vs. P-Value in Hypothesis Testing
In the realm of statistical analysis, critical values and p-values serve as essential tools for hypothesis testing and decision making. These concepts, rooted in the work of statisticians like Ronald Fisher and the Neyman-Pearson approach, play a crucial role in determining statistical significance. Understanding the distinction between critical values and p-values is vital for researchers and data analysts to interpret their findings accurately and avoid misinterpretations that can lead to false positives or false negatives.
This article aims to shed light on the key differences between critical values and p-values in hypothesis testing. It will explore the definition and calculation of critical values, including how to find critical values using tables or calculators. The discussion will also cover p-values, their interpretation, and their relationship to significance levels. Additionally, the article will address common pitfalls in result interpretation and provide guidance on when to use critical values versus p-values in various statistical scenarios, such as t-tests and confidence intervals.
What is a Critical Value?
Definition and concept.
A critical value in statistics serves as a crucial cut-off point in hypothesis testing and decision making. It defines the boundary between accepting and rejecting the null hypothesis, playing a vital role in determining statistical significance. The critical value is intrinsically linked to the significance level (α) chosen for the test, which represents the probability of making a Type I error.
Critical values are essential for accurately representing a range of characteristics within a dataset. They help statisticians calculate the margin of error and provide insights into the validity and accuracy of their findings. In hypothesis testing, the critical value is compared to the obtained test statistic to determine whether the null hypothesis should be rejected or not.
How to calculate critical values
Calculating critical values involves several steps and depends on the type of test being conducted. The general formula for finding the critical value is:
Critical probability (p*) = 1 – (Alpha / 2)
Where Alpha = 1 – (confidence level / 100)
For example, using a confidence level of 95%, the alpha value would be:
Alpha value = 1 – (95/100) = 0.05
Then, the critical probability would be:
Critical probability (p*) = 1 – (0.05 / 2) = 0.975
The critical value can be expressed in two ways:
- As a Z-score related to cumulative probability
- As a critical t statistic, which is equal to the critical probability
For larger sample sizes (typically n ≥ 30), the Z-score is used, while for smaller samples or when the population standard deviation is unknown, the t statistic is more appropriate.
Examples in hypothesis testing
Critical values play a crucial role in various types of hypothesis tests. Here are some examples:
- One-tailed test: For a right-tailed test with H₀: μ = 3 vs. H₁: μ > 3, the critical value would be the t-value such that the probability to the right of it is α. For instance, with α = 0.05 and 14 degrees of freedom, the critical value t₀.₀₅,₁₄ is 1.7613 . The null hypothesis would be rejected if the test statistic t is greater than 1.7613.
- Two-tailed test: For a two-tailed test with H₀: μ = 3 vs. H₁: μ ≠ 3, there are two critical values – one for each tail. Using α = 0.05 and 14 degrees of freedom, the critical values would be -2.1448 and 2.1448 . The null hypothesis would be rejected if the test statistic t is less than -2.1448 or greater than 2.1448.
- Z-test example: In a tire manufacturing plant producing 15.2 tires per hour with a variance of 2.5, new machines were tested. The critical region for a one-tailed test with α = 0.10 was z > 1.282. The calculated z-statistic of 3.51 exceeded this critical value , leading to the rejection of the null hypothesis.
Understanding critical values is essential for making informed decisions in hypothesis testing and statistical analysis. They provide a standardized approach to evaluating the significance of research findings and help researchers avoid misinterpretations that could lead to false positives or false negatives.
Understanding P-Values
Definition of p-value
In statistical hypothesis testing, a p-value is a crucial concept that helps researchers quantify the strength of evidence against the null hypothesis. The p-value is defined as the probability of obtaining test results at least as extreme as the observed results, assuming that the null hypothesis is true. This definition highlights the relationship between the p-value and the null hypothesis, which is fundamental to understanding its interpretation.
The p-value serves as an alternative to rejection points, providing the smallest level of significance at which the null hypothesis would be rejected. It is important to note that the p-value is not the probability that the null hypothesis is true or that the alternative hypothesis is false. Rather, it indicates how compatible the observed data are with a specified statistical model, typically the null hypothesis.
Interpreting p-values
Interpreting p-values correctly is essential for making sound statistical inferences. A smaller p-value suggests stronger evidence against the null hypothesis and in favor of the alternative hypothesis. Conventionally, a p-value of 0.05 or lower is considered statistically significant, leading to the rejection of the null hypothesis. However, it is crucial to understand that this threshold is arbitrary and should not be treated as a definitive cutoff point for decision-making.
When interpreting p-values, it is important to consider the following:
- The p-value does not indicate the size or importance of the observed effect. A small p-value can be observed for an effect that is not meaningful or important, especially with large sample sizes.
- The p-value is not the probability that the observed effects were produced by random chance alone. It is calculated under the assumption that the null hypothesis is true.
- A p-value greater than 0.05 does not necessarily mean that the null hypothesis is true or that there is no effect. It simply indicates that the evidence against the null hypothesis is not strong enough to reject it at the chosen significance level.
Common misconceptions about p-values
Despite their widespread use, p-values are often misinterpreted in scientific research and education. Some common misconceptions include:
- Interpreting the p-value as the probability that the null hypothesis is true or the probability that the alternative hypothesis is false. This interpretation is incorrect, as p-values do not provide direct probabilities for hypotheses.
- Believing that a p-value less than 0.05 proves that a finding is true or that the probability of making a mistake is less than 5%. In reality, the p-value is a statement about the relation of the data to the null hypothesis, not a measure of truth or error rates.
- Treating p-values on opposite sides of the 0.05 threshold as qualitatively different. This dichotomous thinking can lead to overemphasis on statistical significance and neglect of practical significance.
- Using p-values to determine the size or importance of an effect. P-values do not provide information about effect sizes or clinical relevance.
To address these misconceptions, it is important to consider p-values as continuous measures of evidence rather than binary indicators of significance. Additionally, researchers should focus on reporting effect sizes, confidence intervals, and practical significance alongside p-values to provide a more comprehensive understanding of their findings.
Key Differences Between Critical Values and P-Values
Approach to hypothesis testing
Critical values and p-values represent two distinct approaches to hypothesis testing, each offering unique insights into the decision-making process. The critical value approach, rooted in traditional hypothesis testing, establishes a clear boundary for accepting or rejecting the null hypothesis. This method is closely tied to significance levels and provides a straightforward framework for statistical inference.
In contrast, p-values offer a continuous measure of evidence against the null hypothesis. This approach allows for a more nuanced evaluation of the data’s compatibility with the null hypothesis. While both methods aim to support or reject the null hypothesis, they differ in how they lead to that decision.
Decision-making process
The decision-making process for critical values and p-values follows different paths. Critical values provide a binary framework, simplifying the decision to either reject or fail to reject the null hypothesis. This approach streamlines the process by classifying results as significant or not significant based on predetermined thresholds.
For instance, in a hypothesis test with a significance level (α) of 0.05 , the critical value serves as the dividing line between the rejection and non-rejection regions. If the test statistic exceeds the critical value, the null hypothesis is rejected.
P-values, on the other hand, offer a more flexible approach to decision-making. Instead of a simple yes or no answer, p-values present a range of evidence levels against the null hypothesis. This continuous scale allows researchers to interpret the strength of evidence and choose an appropriate significance level for their specific context.
Interpretation of results
The interpretation of results differs significantly between critical values and p-values. Critical values provide a clear-cut interpretation: if the test statistic falls within the rejection region defined by the critical value, the null hypothesis is rejected. This approach offers a straightforward way to communicate results, especially when a binary decision is required.
P-values, however, offer a more nuanced interpretation of results. A smaller p-value indicates stronger evidence against the null hypothesis. For example, a p-value of 0.03 suggests more compelling evidence against the null hypothesis than a p-value of 0.07. This continuous scale allows for a more detailed assessment of the data’s compatibility with the null hypothesis.
It’s important to note that while a p-value of 0.05 is often used as a threshold for statistical significance, this is an arbitrary cutoff. The interpretation of p-values should consider the context of the study and the potential for practical significance.
Both approaches have their strengths and limitations. Critical values simplify decision-making but may not accurately reflect the increasing precision of estimates as sample sizes grow. P-values provide a more comprehensive understanding of outcomes, especially when combined with effect size measures. However, they are frequently misunderstood and can be affected by sample size in large datasets, potentially leading to misleading significance.
In conclusion, while critical values and p-values are both essential tools in hypothesis testing, they offer different perspectives on statistical inference. Critical values provide a clear, binary decision framework, while p-values allow for a more nuanced evaluation of evidence against the null hypothesis. Understanding these differences is crucial for researchers to choose the most appropriate method for their specific research questions and to interpret results accurately.
When to Use Critical Values vs. P-Values
Advantages of critical value approach.
The critical value approach offers several advantages in hypothesis testing. It provides a simple, binary framework for decision-making, allowing researchers to either reject or fail to reject the null hypothesis. This method is particularly useful when a clear explanation of the significance of results is required. Critical values are especially beneficial in sectors where decision-making is influenced by predetermined thresholds, such as the commonly used 0.05 significance level.
One of the key strengths of the critical value approach is its consistency with accepted significance levels, which simplifies interpretation. This method is particularly valuable in non-parametric tests where distributional assumptions may be violated. The critical value approach involves comparing the observed test statistic to a predetermined cutoff value. If the test statistic is more extreme than the critical value, the null hypothesis is rejected in favor of the alternative hypothesis.
Benefits of p-value method
The p-value method offers a more nuanced approach to hypothesis testing. It provides a continuous scale for evaluating the strength of evidence against the null hypothesis, allowing researchers to interpret data with greater flexibility. This approach is particularly useful when conducting unique or exploratory research, as it enables scientists to choose an appropriate level of significance based on their specific context.
P-values quantify the probability of observing a test statistic as extreme as, or more extreme than, the one observed, assuming the null hypothesis is true. This method provides a more comprehensive understanding of outcomes, especially when combined with effect size measures. For instance, a p-value of 0.0127 indicates that it is unlikely to observe such an extreme test statistic if the null hypothesis were true, leading to its rejection.
Choosing the right approach for your study
The choice between critical values and p-values depends on various factors, including the nature of the data , study design, and research objectives. Critical values are best suited for situations requiring a simple, binary choice about the null hypothesis. They streamline the decision-making process by classifying results as significant or not significant.
On the other hand, p-values are more appropriate when evaluating the strength of evidence against the null hypothesis on a continuous scale. They offer a more subtle understanding of the data’s significance and allow for flexibility in interpretation. However, it’s crucial to note that p-values have been subject to debate and controversy, particularly in the context of analyzing complex data associated with plant and animal breeding programs.
When choosing between these approaches, consider the following:
- If you need a clear-cut decision based on predetermined thresholds, the critical value approach may be more suitable.
- For a more nuanced interpretation of results, especially in exploratory research, the p-value method might be preferable.
- Consider the potential for misinterpretation and misuse associated with p-values, such as p-value hacking , which can lead to inflated significance and misleading conclusions.
Ultimately, the choice between critical values and p-values should be guided by the specific requirements of your study and the need for accurate statistical inferences to make informed decisions in your field of research.
Common Pitfalls in Interpreting Results
Overreliance on arbitrary thresholds.
One of the most prevalent issues in statistical analysis is the overreliance on arbitrary thresholds, particularly the p-value of 0.05. This threshold has been widely used for decades to determine statistical significance, but its arbitrary nature has come under scrutiny. Many researchers argue that setting a single threshold for all sciences is too extreme and can lead to misleading conclusions.
The use of p-values as the sole measure of significance can result in the publication of potentially false or misleading results. It’s crucial to understand that statistical significance does not necessarily equate to practical significance or real-world importance. A study with a large sample size can produce statistically significant results even when the effect size is trivial.
To address this issue, some researchers propose selecting and justifying p-value thresholds for experiments before collecting any data. These levels would be based on factors such as the potential impact of a discovery or how surprising it would be. However, this approach also has its critics, who argue that researchers may not have the incentive to use more stringent thresholds of evidence.
Ignoring effect sizes
Another common pitfall in interpreting results is the tendency to focus solely on statistical significance while ignoring effect sizes. Effect size is a crucial measure that indicates the magnitude of the relationship between variables or the difference between groups. It provides information about the practical significance of research findings, which is often more valuable than mere statistical significance.
Unlike p-values, effect sizes are independent of sample size. This means they offer a more reliable measure of the practical importance of a result, especially when dealing with large datasets. Researchers should report effect sizes alongside p-values to provide a comprehensive understanding of their findings.
It’s important to note that the criteria for small or large effect sizes may vary depending on the research field. Therefore, it’s essential to consider the context and norms within a particular area of study when interpreting effect sizes.
Misinterpreting statistical vs. practical significance
The distinction between statistical and practical significance is often misunderstood or overlooked in research. Statistical significance, typically determined by p-values, indicates the probability that the observed results occurred by chance. However, it does not provide information about the magnitude or practical importance of the effect.
Practical significance, on the other hand, refers to the real-world relevance or importance of the research findings. A result can be statistically significant but practically insignificant, or vice versa. For instance, a study with a large sample size might find a statistically significant difference between two groups, but the actual difference may be too small to have any meaningful impact in practice.
To avoid this pitfall, researchers should focus on both statistical and practical significance when interpreting their results. This involves considering not only p-values but also effect sizes, confidence intervals, and the potential real-world implications of the findings. Additionally, it’s crucial to interpret results in the context of the specific research question and field of study.
By addressing these common pitfalls, researchers can improve the quality and relevance of their statistical analyzes. This approach will lead to more meaningful interpretations of results and better-informed decision-making in various fields of study.
Critical values and p-values are key tools in statistical analysis, each offering unique benefits to researchers. These concepts help in making informed decisions about hypotheses and understanding the significance of findings. While critical values provide a clear-cut approach for decision-making, p-values offer a more nuanced evaluation of evidence against the null hypothesis. Understanding their differences and proper use is crucial to avoid common pitfalls in result interpretation.
Ultimately, the choice between critical values and p-values depends on the specific needs of a study and the context of the research. It’s essential to consider both statistical and practical significance when interpreting results, and to avoid overreliance on arbitrary thresholds. By using these tools wisely, researchers can enhance the quality and relevance of their statistical analyzes, leading to more meaningful insights and better-informed decisions.
1. When should you use a critical value as opposed to a p-value in hypothesis testing?
When testing a hypothesis, compare the p-value directly with the significance level (α). If the p-value is less than α, reject the null hypothesis (H0); if it’s greater, do not reject H0. Conversely, using critical values allows you to determine whether the p-value is greater or less than α.
2. What does it mean if the p-value is less than the critical value?
If the p-value is lower than the critical value, you should reject the null hypothesis. Conversely, if the p-value is equal to or greater than the critical value, you should not reject the null hypothesis. Remember, a smaller p-value generally indicates stronger evidence against the null hypothesis.
3. What is the purpose of a critical value in statistical testing?
The critical value is a point on the test statistic that defines the boundaries of the acceptance or rejection regions for a statistical test. It helps in setting the threshold for what constitutes statistically significant results.
4. When should you reject the null hypothesis based on the critical value?
In the critical value approach, if the test statistic is more extreme than the critical value, reject the null hypothesis. If it is less extreme, do not reject the null hypothesis. This method helps in deciding the statistical significance of the test results.
Unlock the power of data science & AI with Tesseract Academy! Dive into our data science & AI courses to elevate your skills and discover endless possibilities in this new era.
- Podcast: ChatGPT and the future of AI with Mark van Rijmenam
- Nifty vs Sensex: Key Differences Explained
- The Human Touch: How AI Voice Generators Aim to Replicate Natural Speech Patterns
- Optimizing Website Performance: The Impact of Server Location
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
How Hypothesis Tests Work: Significance Levels (Alpha) and P values
By Jim Frost 45 Comments
Hypothesis testing is a vital process in inferential statistics where the goal is to use sample data to draw conclusions about an entire population . In the testing process, you use significance levels and p-values to determine whether the test results are statistically significant.
You hear about results being statistically significant all of the time. But, what do significance levels, P values, and statistical significance actually represent? Why do we even need to use hypothesis tests in statistics?
In this post, I answer all of these questions. I use graphs and concepts to explain how hypothesis tests function in order to provide a more intuitive explanation. This helps you move on to understanding your statistical results.
Hypothesis Test Example Scenario
To start, I’ll demonstrate why we need to use hypothesis tests using an example.
A researcher is studying fuel expenditures for families and wants to determine if the monthly cost has changed since last year when the average was $260 per month. The researcher draws a random sample of 25 families and enters their monthly costs for this year into statistical software. You can download the CSV data file: FuelsCosts . Below are the descriptive statistics for this year.

We’ll build on this example to answer the research question and show how hypothesis tests work.
Descriptive Statistics Alone Won’t Answer the Question
The researcher collected a random sample and found that this year’s sample mean (330.6) is greater than last year’s mean (260). Why perform a hypothesis test at all? We can see that this year’s mean is higher by $70! Isn’t that different?
Regrettably, the situation isn’t as clear as you might think because we’re analyzing a sample instead of the full population. There are huge benefits when working with samples because it is usually impossible to collect data from an entire population. However, the tradeoff for working with a manageable sample is that we need to account for sample error.
The sampling error is the gap between the sample statistic and the population parameter. For our example, the sample statistic is the sample mean, which is 330.6. The population parameter is μ, or mu, which is the average of the entire population. Unfortunately, the value of the population parameter is not only unknown but usually unknowable. Learn more about Sampling Error .
We obtained a sample mean of 330.6. However, it’s conceivable that, due to sampling error, the mean of the population might be only 260. If the researcher drew another random sample, the next sample mean might be closer to 260. It’s impossible to assess this possibility by looking at only the sample mean. Hypothesis testing is a form of inferential statistics that allows us to draw conclusions about an entire population based on a representative sample. We need to use a hypothesis test to determine the likelihood of obtaining our sample mean if the population mean is 260.
Background information : The Difference between Descriptive and Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
A Sampling Distribution Determines Whether Our Sample Mean is Unlikely
It is very unlikely for any sample mean to equal the population mean because of sample error. In our case, the sample mean of 330.6 is almost definitely not equal to the population mean for fuel expenditures.
If we could obtain a substantial number of random samples and calculate the sample mean for each sample, we’d observe a broad spectrum of sample means. We’d even be able to graph the distribution of sample means from this process.
This type of distribution is called a sampling distribution. You obtain a sampling distribution by drawing many random samples of the same size from the same population. Why the heck would we do this?
Because sampling distributions allow you to determine the likelihood of obtaining your sample statistic and they’re crucial for performing hypothesis tests.
Luckily, we don’t need to go to the trouble of collecting numerous random samples! We can estimate the sampling distribution using the t-distribution, our sample size, and the variability in our sample.
We want to find out if the average fuel expenditure this year (330.6) is different from last year (260). To answer this question, we’ll graph the sampling distribution based on the assumption that the mean fuel cost for the entire population has not changed and is still 260. In statistics, we call this lack of effect, or no change, the null hypothesis . We use the null hypothesis value as the basis of comparison for our observed sample value.
Sampling distributions and t-distributions are types of probability distributions.
Related posts : Sampling Distributions and Understanding Probability Distributions
Graphing our Sample Mean in the Context of the Sampling Distribution
The graph below shows which sample means are more likely and less likely if the population mean is 260. We can place our sample mean in this distribution. This larger context helps us see how unlikely our sample mean is if the null hypothesis is true (μ = 260).

The graph displays the estimated distribution of sample means. The most likely values are near 260 because the plot assumes that this is the true population mean. However, given random sampling error, it would not be surprising to observe sample means ranging from 167 to 352. If the population mean is still 260, our observed sample mean (330.6) isn’t the most likely value, but it’s not completely implausible either.
The Role of Hypothesis Tests
The sampling distribution shows us that we are relatively unlikely to obtain a sample of 330.6 if the population mean is 260. Is our sample mean so unlikely that we can reject the notion that the population mean is 260?
In statistics, we call this rejecting the null hypothesis. If we reject the null for our example, the difference between the sample mean (330.6) and 260 is statistically significant. In other words, the sample data favor the hypothesis that the population average does not equal 260.
However, look at the sampling distribution chart again. Notice that there is no special location on the curve where you can definitively draw this conclusion. There is only a consistent decrease in the likelihood of observing sample means that are farther from the null hypothesis value. Where do we decide a sample mean is far away enough?
To answer this question, we’ll need more tools—hypothesis tests! The hypothesis testing procedure quantifies the unusualness of our sample with a probability and then compares it to an evidentiary standard. This process allows you to make an objective decision about the strength of the evidence.
We’re going to add the tools we need to make this decision to the graph—significance levels and p-values!
These tools allow us to test these two hypotheses:
- Null hypothesis: The population mean equals the null hypothesis mean (260).
- Alternative hypothesis: The population mean does not equal the null hypothesis mean (260).
Related post : Hypothesis Testing Overview
What are Significance Levels (Alpha)?
A significance level, also known as alpha or α, is an evidentiary standard that a researcher sets before the study. It defines how strongly the sample evidence must contradict the null hypothesis before you can reject the null hypothesis for the entire population. The strength of the evidence is defined by the probability of rejecting a null hypothesis that is true. In other words, it is the probability that you say there is an effect when there is no effect.
For instance, a significance level of 0.05 signifies a 5% risk of deciding that an effect exists when it does not exist.
Lower significance levels require stronger sample evidence to be able to reject the null hypothesis. For example, to be statistically significant at the 0.01 significance level requires more substantial evidence than the 0.05 significance level. However, there is a tradeoff in hypothesis tests. Lower significance levels also reduce the power of a hypothesis test to detect a difference that does exist.
The technical nature of these types of questions can make your head spin. A picture can bring these ideas to life!
To learn a more conceptual approach to significance levels, see my post about Understanding Significance Levels .
Graphing Significance Levels as Critical Regions
On the probability distribution plot, the significance level defines how far the sample value must be from the null value before we can reject the null. The percentage of the area under the curve that is shaded equals the probability that the sample value will fall in those regions if the null hypothesis is correct.
To represent a significance level of 0.05, I’ll shade 5% of the distribution furthest from the null value.

The two shaded regions in the graph are equidistant from the central value of the null hypothesis. Each region has a probability of 0.025, which sums to our desired total of 0.05. These shaded areas are called the critical region for a two-tailed hypothesis test.
The critical region defines sample values that are improbable enough to warrant rejecting the null hypothesis. If the null hypothesis is correct and the population mean is 260, random samples (n=25) from this population have means that fall in the critical region 5% of the time.
Our sample mean is statistically significant at the 0.05 level because it falls in the critical region.
Related posts : One-Tailed and Two-Tailed Tests Explained , What Are Critical Values? , and T-distribution Table of Critical Values
Comparing Significance Levels
Let’s redo this hypothesis test using the other common significance level of 0.01 to see how it compares.

This time the sum of the two shaded regions equals our new significance level of 0.01. The mean of our sample does not fall within with the critical region. Consequently, we fail to reject the null hypothesis. We have the same exact sample data, the same difference between the sample mean and the null hypothesis value, but a different test result.
What happened? By specifying a lower significance level, we set a higher bar for the sample evidence. As the graph shows, lower significance levels move the critical regions further away from the null value. Consequently, lower significance levels require more extreme sample means to be statistically significant.
You must set the significance level before conducting a study. You don’t want the temptation of choosing a level after the study that yields significant results. The only reason I compared the two significance levels was to illustrate the effects and explain the differing results.
The graphical version of the 1-sample t-test we created allows us to determine statistical significance without assessing the P value. Typically, you need to compare the P value to the significance level to make this determination.
Related post : Step-by-Step Instructions for How to Do t-Tests in Excel
What Are P values?
P values are the probability that a sample will have an effect at least as extreme as the effect observed in your sample if the null hypothesis is correct.
This tortuous, technical definition for P values can make your head spin. Let’s graph it!
First, we need to calculate the effect that is present in our sample. The effect is the distance between the sample value and null value: 330.6 – 260 = 70.6. Next, I’ll shade the regions on both sides of the distribution that are at least as far away as 70.6 from the null (260 +/- 70.6). This process graphs the probability of observing a sample mean at least as extreme as our sample mean.

The total probability of the two shaded regions is 0.03112. If the null hypothesis value (260) is true and you drew many random samples, you’d expect sample means to fall in the shaded regions about 3.1% of the time. In other words, you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true. That’s the P value!
Learn more about How to Find the P Value .
Using P values and Significance Levels Together
If your P value is less than or equal to your alpha level, reject the null hypothesis.
The P value results are consistent with our graphical representation. The P value of 0.03112 is significant at the alpha level of 0.05 but not 0.01. Again, in practice, you pick one significance level before the experiment and stick with it!
Using the significance level of 0.05, the sample effect is statistically significant. Our data support the alternative hypothesis, which states that the population mean doesn’t equal 260. We can conclude that mean fuel expenditures have increased since last year.
P values are very frequently misinterpreted as the probability of rejecting a null hypothesis that is actually true. This interpretation is wrong! To understand why, please read my post: How to Interpret P-values Correctly .
Discussion about Statistically Significant Results
Hypothesis tests determine whether your sample data provide sufficient evidence to reject the null hypothesis for the entire population. To perform this test, the procedure compares your sample statistic to the null value and determines whether it is sufficiently rare. “Sufficiently rare” is defined in a hypothesis test by:
- Assuming that the null hypothesis is true—the graphs center on the null value.
- The significance (alpha) level—how far out from the null value is the critical region?
- The sample statistic—is it within the critical region?
There is no special significance level that correctly determines which studies have real population effects 100% of the time. The traditional significance levels of 0.05 and 0.01 are attempts to manage the tradeoff between having a low probability of rejecting a true null hypothesis and having adequate power to detect an effect if one actually exists.
The significance level is the rate at which you incorrectly reject null hypotheses that are actually true ( type I error ). For example, for all studies that use a significance level of 0.05 and the null hypothesis is correct, you can expect 5% of them to have sample statistics that fall in the critical region. When this error occurs, you aren’t aware that the null hypothesis is correct, but you’ll reject it because the p-value is less than 0.05.
This error does not indicate that the researcher made a mistake. As the graphs show, you can observe extreme sample statistics due to sample error alone. It’s the luck of the draw!
Related posts : Statistical Significance: Definition & Meaning and Types of Errors in Hypothesis Testing
Hypothesis tests are crucial when you want to use sample data to make conclusions about a population because these tests account for sample error. Using significance levels and P values to determine when to reject the null hypothesis improves the probability that you will draw the correct conclusion.
Keep in mind that statistical significance doesn’t necessarily mean that the effect is important in a practical, real-world sense. For more information, read my post about Practical vs. Statistical Significance .
If you like this post, read the companion post: How Hypothesis Tests Work: Confidence Intervals and Confidence Levels .
You can also read my other posts that describe how other tests work:
- How t-Tests Work
- How the F-test works in ANOVA
- How Chi-Squared Tests of Independence Work
To see an alternative approach to traditional hypothesis testing that does not use probability distributions and test statistics, learn about bootstrapping in statistics !
Share this:

Reader Interactions
December 11, 2022 at 10:56 am
For very easy concept about level of significance & p-value 1.Teacher has given a one assignment to student & asked how many error you have doing this assignment? Student reply, he can has error ≤ 5% (it is level of significance). After completion of assignment, teacher checked his error which is ≤ 5% (may be 4% or 3% or 2% even less, it is p-value) it means his results are significant. Otherwise he has error > 5% (may be 6% or 7% or 8% even more, it is p-value) it means his results are non-significant. 2. Teacher has given a one assignment to student & asked how many error you have doing this assignment? Student reply, he can has error ≤ 1% (it is level of significance). After completion of assignment, teacher checked his error which is ≤ 1% (may be 0.9% or 0.8% or 0.7% even less, it is p-value) it means his results are significant. Otherwise he has error > 1% (may be 1.1% or 1.5% or 2% even more, it is p-value) it means his results are non-significant. p-value is significant or not mainly dependent upon the level of significance.
December 11, 2022 at 7:50 pm
I think that approach helps explain how to determine statistical significance–is the p-value less than or equal to the significance level. However, it doesn’t really explain what statistical significance means. I find that comparing the p-value to the significance level is the easy part. Knowing what it means and how to choose your significance level is the harder part!
December 3, 2022 at 5:54 pm
What would you say to someone who believes that a p-value higher than the level of significance (alpha) means the null hypothesis has been proven? Should you support that statement or deny it?
December 3, 2022 at 10:18 pm
Hi Emmanuel,
When the p-value is greater than the significance level, you fail to reject the null hypothesis . That is different than proving it. To learn why and what it means, click the link to read a post that I’ve written that will answer your question!
April 19, 2021 at 12:27 am
Thank you so much Sir
April 18, 2021 at 2:37 pm
Hi sir, your blogs are much more helpful for clearing the concepts of statistics, as a researcher I find them much more useful. I have some quarries:
1. In many research papers I have seen authors using the statement ” means or values are statically at par at p = 0.05″ when they do some pair wise comparison between the treatments (a kind of post hoc) using some value of CD (critical difference) or we can say LSD which is calculated using alpha not using p. So with this article I think this should be alpha =0.05 or 5%, not p = 0.05 earlier I thought p and alpha are same. p it self is compared with alpha 0.05. Correct me if I am wrong.
2. When we can draw a conclusion using critical value based on critical values (CV) which is based on alpha values in different tests (e.g. in F test CV is at F (0.05, t-1, error df) when alpha is 0.05 which is table value of F and is compared with F calculated for drawing the conclusion); then why we go for p values, and draw a conclusion based on p values, even many online software do not give p value, they just mention CD (LSD)
3. can you please help me in interpreting interaction in two factor analysis (Factor A X Factor b) in Anova.
Thank You so much!
(Commenting again as I have not seen my comment in comment list; don’t know why)
April 18, 2021 at 10:57 pm
Hi Himanshu,
I manually approve comments so there will be some time lag involved before they show up.
Regarding your first question, yes, you’re correct. Test results are significant at particular significance levels or alpha. They should not use p to define the significance level. You’re also correct in that you compare p to alpha.
Critical values are a different (but related) approach for determining significance. It was more common before computer analysis took off because it reduced the calculations. Using this approach in its simplest form, you only know whether a result is significant or not at the given alpha. You just determine whether the test statistic falls within a critical region to determine statistical significance or not significant. However, it is ok to supplement this type of result with the actual p-value. Knowing the precise p-value provides additional information that significant/not significant does not provide. The critical value and p-value approaches will always agree too. For more information about why the exact p-value is useful, read my post about Five Tips for Interpreting P-values .
Finally, I’ve written about two-way ANOVA in my post, How to do Two-Way ANOVA in Excel . Additionally, I write about it in my Hypothesis Testing ebook .
January 28, 2021 at 3:12 pm
Thank you for your answer, Jim, I really appreciate it. I’m taking a Coursera stats course and online learning without being able to ask questions of a real teacher is not my forte!
You’re right, I don’t think I’m ready for that calculation! However, I think I’m struggling with something far more basic, perhaps even the interpretation of the t-table? I’m just not sure how you came up with the p-value as .03112, with the 24 degrees of freedom. When I pull up a t-table and look at the 24-degrees of freedom row, I’m not sure how any of those numbers correspond with your answer? Either the single tail of 0.01556 or the combined of 0.03112. What am I not getting? (which, frankly, could be a lot!!) Again, thank you SO much for your time.
January 28, 2021 at 11:19 pm
Ah ok, I see! First, let me point you to several posts I’ve written about t-values and the t-distribution. I don’t cover those in this post because I wanted to present a simplified version that just uses the data in its regular units. The basic idea is that the hypothesis tests actually convert all your raw data down into one value for a test statistic, such as the t-value. And then it uses that test statistic to determine whether your results are statistically significant. To be significant, the t-value must exceed a critical value, which is what you lookup in the table. Although, nowadays you’d typically let your software just tell you.
So, read the following two posts, which covers several aspects of t-values and distributions. And then if you have more questions after that, you can post them. But, you’ll have a lot more information about them and probably some of your questions will be answered! T-values T-distributions
January 27, 2021 at 3:10 pm
Jim, just found your website and really appreciate your thoughtful, thorough way of explaining things. I feel very dumb, but I’m struggling with p-values and was hoping you could help me.
Here’s the section that’s getting me confused:
“First, we need to calculate the effect that is present in our sample. The effect is the distance between the sample value and null value: 330.6 – 260 = 70.6. Next, I’ll shade the regions on both sides of the distribution that are at least as far away as 70.6 from the null (260 +/- 70.6). This process graphs the probability of observing a sample mean at least as extreme as our sample mean.
** I’m good up to this point. Draw the picture, do the subtraction, shade the regions. BUT, I’m not sure how to figure out the area of the shaded region — even with a T-table. When I look at the T-table on 24 df, I’m not sure what to do with those numbers, as none of them seem to correspond in any way to what I’m looking at in the problem. In the end, I have no idea how you calculated each shaded area being 0.01556.
I feel like there’s a (very simple) step that everyone else knows how to do, but for some reason I’m missing it.
Again, dumb question, but I’d love your help clarifying that.
thank you, Sara
January 27, 2021 at 9:51 pm
That’s not a dumb question at all. I actually don’t show or explain the calculations for figuring out the area. The reason for that is the same reason why students never calculate the critical t-values for their test, instead you look them up in tables or use statistical software. The common reason for all that is because calculating these values is extremely complicated! It’s best to let software do that for you or, when looking critical values, use the tables!
The principal though is that percentage of the area under the curve equals the probability that values will fall within that range.
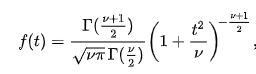
And then, for this example, you’d need to figure out the area under the curve for particular ranges!
January 15, 2021 at 10:57 am
HI Jim, I have a question related to Hypothesis test.. in Medical imaging, there are different way to measure signal intensity (from a tumor lesion for example). I tested for the same 100 patients 4 different ways to measure tumor captation to a injected dose. So for the 100 patients, i got 4 linear regression (relation between injected dose and measured quantity at tumor sites) = so an output of 4 equations Condition A output = -0,034308 + 0,0006602*input Condition B output = 0,0117631 + 0,0005425*input Condition C output = 0,0087871 + 0,0005563*input Condition D output = 0,001911 + 0,0006255*input
My question : i want to compare the 4 methods to find the best one (compared to others) : do Hypothesis test good to me… and if Yes, i do not find test to perform it. Can you suggest me a software. I uselly used JMP for my stats… but open to other softwares…
THank for your time G
November 16, 2020 at 5:42 am
Thank you very much for writing about this topic!
Your explanation made more sense to me about: Why we reject Null Hypothesis when p value < significance level
Kind greetings, Jalal
September 25, 2020 at 1:04 pm
Hi Jim, Your explanations are so helpful! Thank you. I wondered about your first graph. I see that the mean of the graph is 260 from the null hypothesis, and it looks like the standard deviation of the graph is about 31. Where did you get 31 from? Thank you
September 25, 2020 at 4:08 pm
Hi Michelle,
That is a great question. Very observant. And it gets to how these tests work. The hypothesis test that I’m illustrating here is the one-sample t-test. And this graph illustrates the sampling distribution for the t-test. T-tests use the t-distribution to determine the sampling distribution. For the t-distribution, you need to specify the degrees of freedom, which entirely defines the distribution (i.e., it’s the only parameter). For 1-sample t-tests, the degrees of freedom equal the number of observations minus 1. This dataset has 25 observations. Hence, the 24 DF you see in the graph.
Unlike the normal distribution, there is no standard deviation parameter. Instead, the degrees of freedom determines the spread of the curve. Typically, with t-tests, you’ll see results discussed in terms of t-values, both for your sample and for defining the critical regions. However, for this introductory example, I’ve converted the t-values into the raw data units (t-value * SE mean).
So, the standard deviation you’re seeing in the graph is a result of the spread of the underlying t-distribution that has 24 degrees of freedom and then applying the conversion from t-values to raw values.
September 10, 2020 at 8:19 am
Your blog is incredible.
I am having difficulty understanding why the phrase ‘as extreme as’ is required in the definition of p-value (“P values are the probability that a sample will have an effect at least as extreme as the effect observed in your sample if the null hypothesis is correct.”)
Why can’t P-Values simply be defined as “The probability of sample observation if the null hypothesis is correct?”
In your other blog titled ‘Interpreting P values’ you have explained p-values as “P-values indicate the believability of the devil’s advocate case that the null hypothesis is correct given the sample data”. I understand (or accept) this explanation. How does one move from this definition to one that contains the phrase ‘as extreme as’?
September 11, 2020 at 5:05 pm
Thanks so much for your kind words! I’m glad that my website has been helpful!
The key to understanding the “at least as extreme” wording lies in the probability plots for p-values. Using probability plots for continuous data, you can calculate probabilities, but only for ranges of values. I discuss this in my post about understanding probability distributions . In a nutshell, we need a range of values for these probabilities because the probabilities are derived from the area under a distribution curve. A single value just produces a line on these graphs rather than an area. Those ranges are the shaded regions in the probability plots. For p-values, the range corresponds to the “at least as extreme” wording. That’s where it comes from. We need a range to calculate a probability. We can’t use the single value of the observed effect because it doesn’t produce an area under the curve.
I hope that helps! I think this is a particularly confusing part of understanding p-values that most people don’t understand.
August 7, 2020 at 5:45 pm
Hi Jim, thanks for the post.
Could you please clarify the following excerpt from ‘Graphing Significance Levels as Critical Regions’:
“The percentage of the area under the curve that is shaded equals the probability that the sample value will fall in those regions if the null hypothesis is correct.”
I’m not sure if I understood this correctly. If the sample value fall in one of the shaded regions, doesn’t mean that the null hypothesis can be rejected, hence that is not correct?
August 7, 2020 at 10:23 pm
Think of it this way. There are two basic reasons for why a sample value could fall in a critical region:
- The null hypothesis is correct and random chance caused the sample value to be unusual.
- The null hypothesis is not correct.
You don’t know which one is true. Remember, just because you reject the null hypothesis it doesn’t mean the null is false. However, by using hypothesis tests to determine statistical significance, you control the chances of #1 occurring. The rate at which #1 occurs equals your significance level. On the hand, you don’t know the probability of the sample value falling in a critical region if the alternative hypothesis is correct (#2). It depends on the precise distribution for the alternative hypothesis and you usually don’t know that, which is why you’re testing the hypotheses in the first place!
I hope I answered the question you were asking. If not, feel free to ask follow up questions. Also, this ties into how to interpret p-values . It’s not exactly straightforward. Click the link to learn more.
June 4, 2020 at 6:17 am
Hi Jim, thank you very much for your answer. You helped me a lot!
June 3, 2020 at 5:23 pm
Hi, Thanks for this post. I’ve been learning a lot with you. My question is regarding to lack of fit. The p-value of my lack of fit is really low, making my lack of fit significant, meaning my model does not fit well. Is my case a “false negative”? given that my pure error is really low, making the computation of the lack of fit low. So it means my model is good. Below I show some information, that I hope helps to clarify my question.
SumSq DF MeanSq F pValue ________ __ ________ ______ __________
Total 1246.5 18 69.25 Model 1241.7 6 206.94 514.43 9.3841e-14 . Linear 1196.6 3 398.87 991.53 1.2318e-14 . Nonlinear 45.046 3 15.015 37.326 2.3092e-06 Residual 4.8274 12 0.40228 . Lack of fit 4.7388 7 0.67698 38.238 0.0004787 . Pure error 0.088521 5 0.017704
June 3, 2020 at 7:53 pm
As you say, a low p-value for a lack of fit test indicates that the model doesn’t fit your data adequately. This is a positive result for the test, which means it can’t be a “false negative.” At best, it could be a false positive, meaning that your data actually fit model well despite the low p-value.
I’d recommend graphing the residuals and looking for patterns . There is probably a relationship between variables that you’re not modeling correctly, such as curvature or interaction effects. There’s no way to diagnose the specific nature of the lack-of-fit problem by using the statistical output. You’ll need the graphs.
If there are no patterns in the residual plots, then your lack-of-fit results might be a false positive.
I hope this helps!
May 30, 2020 at 6:23 am
First of all, I have to say there are not many resources that explain a complicated topic in an easier manner.
My question is, how do we arrive at “if p value is less than alpha, we reject the null hypothesis.”
Is this covered in a separate article I could read?
Thanks Shekhar
May 25, 2020 at 12:21 pm
Hi Jim, terrific website, blog, and after this I’m ordering your book. One of my biggest challenges is nomenclature, definitions, context, and formulating the hypotheses. Here’s one I want to double-be-sure I understand: From above you write: ” These tools allow us to test these two hypotheses:
Null hypothesis: The population mean equals the null hypothesis mean (260). Alternative hypothesis: The population mean does not equal the null hypothesis mean (260). ” I keep thinking that 260 is the population mean mu, the underlying population (that we never really know exactly) and that the Null Hypothesis is comparing mu to x-bar (the sample mean of the 25 families randomly sampled w mean = sample mean = x-bar = 330.6).
So is the following incorrect, and if so, why? Null hypothesis: The population mean mu=260 equals the null hypothesis mean x-bar (330.6). Alternative hypothesis: The population mean mu=269 does not equal the null hypothesis mean x-bar (330.6).
And my thinking is that usually the formulation of null and alternative hypotheses is “test value” = “mu current of underlying population”, whereas I read the formulation on the webpage above to be the reverse.
Any comments appreciated. Many Thanks,
May 26, 2020 at 8:56 pm
The null hypothesis states that population value equals the null value. Now, I know that’s not particularly helpful! But, the null value varies based on test and context. So, in this example, we’re setting the null value aa $260, which was the mean from the previous year. So, our null hypothesis states:
Null: the population mean (mu) = 260. Alternative: the population mean ≠ 260.
These hypothesis statements are about the population parameter. For this type of one-sample analysis, the target or reference value you specify is the null hypothesis value. Additionally, you don’t include the sample estimate in these statements, which is the X-bar portion you tacked on at the end. It’s strictly about the value of the population parameter you’re testing. You don’t know the value of the underlying distribution. However, given the mutually exclusive nature of the null and alternative hypothesis, you know one or the other is correct. The null states that mu equals 260 while the alternative states that it doesn’t equal 260. The data help you decide, which brings us to . . .
However, the procedure does compare our sample data to the null hypothesis value, which is how it determines how strong our evidence is against the null hypothesis.
I hope I answered your question. If not, please let me know!
May 8, 2020 at 6:00 pm
Really using the interpretation “In other words, you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true”, our head seems to tie a knot. However, doing the reverse interpretation, it is much more intuitive and easier. That is, we will observe the sample effect of at least 70.6 in about 96.9% of the time, if the null is false (that is, our hypothesis is true).
May 8, 2020 at 7:25 pm
Your phrasing really isn’t any simpler. And it has the additional misfortune of being incorrect.
What you’re essentially doing is creating a one-sided confidence interval by using the p-value from a two-sided test. That’s incorrect in two ways.
- Don’t mix and match one-sided and two-sided test results.
- Confidence levels are determine by the significance level, not p-values.
So, what you need is a two-sided 95% CI (1-alpha). You could then state the results are statistically significant and you have 95% confidence that the population effect is between X and Y. If you want a lower bound as you propose, then you’ll need to use a one-sided hypothesis test with a 95% Lower Bound. That’ll give you a different value for the lower bound than the one you use.
I like confidence intervals. As I write elsewhere, I think they’re easier to understand and provide more information than a binary test result. But, you need to use them correctly!
One other point. When you are talking about p-values, it’s always under the assumption that the null hypothesis is correct. You *never* state anything about the p-value in relation to the null being false (i.e. alternative is true). But, if you want to use the type of phrasing you suggest, use it in the context of CIs and incorporate the points I cover above.
February 10, 2020 at 11:13 am
Muchas gracias profesor por compartir sus conocimientos. Un saliud especial desde Colombia.
August 6, 2019 at 11:46 pm
i found this really helpful . also can you help me out ?
I’m a little confused Can you tell me if level of significance and pvalue are comparable or not and if they are what does it mean if pvalue < LS . Do we reject the null hypothesis or do we accept the null hypothesis ?
August 7, 2019 at 12:49 am
Hi Divyanshu,
Yes, you compare the p-value to the significance level. When the p-value is less than the significance level (alpha), your results are statistically significant and you reject the null hypothesis.
I’d suggest re-reading the “Using P values and Significance Levels Together” section near the end of this post more closely. That describes the process. The next section describes what it all means.
July 1, 2019 at 4:19 am
sure.. I will use only in my class rooms that too offline with due credits to your orginal page. I will encourage my students to visit your blog . I have purchased your eBook on Regressions….immensely useful.
July 1, 2019 at 9:52 am
Hi Narasimha, that sounds perfect. Thanks for buying my ebook as well. I’m thrilled to hear that you’ve found it to be helpful!
June 28, 2019 at 6:22 am
I have benefited a lot by your writings….Can I share the same with my students in the classroom?
June 30, 2019 at 8:44 pm
Hi Narasimha,
Yes, you can certainly share with your students. Please attribute my original page. And please don’t copy whole sections of my posts onto another webpage as that can be bad with Google! Thanks!
February 11, 2019 at 7:46 pm
Hello, great site and my apologies if the answer to the following question exists already.
I’ve always wondered why we put the sampling distribution about the null hypothesis rather than simply leave it about the observed mean. I can see mathematically we are measuring the same distance from the null and basically can draw the same conclusions.
For example we take a sample (say 50 people) we gather an observation (mean wage) estimate the standard error in that observation and so can build a sampling distribution about the observed mean. That sampling distribution contains a confidence interval, where say, i am 95% confident the true mean lies (i.e. in repeated sampling the true mean would reside within this interval 95% of the time).
When i use this for a hyp-test, am i right in saying that we place the sampling dist over the reference level simply because it’s mathematically equivalent and it just seems easier to gauge how far the observation is from 0 via t-stats or its likelihood via p-values?
It seems more natural to me to look at it the other way around. leave the sampling distribution on the observed value, and then look where the null sits…if it’s too far left or right then it is unlikely the true population parameter is what we believed it to be, because if the null were true it would only occur ~ 5% of the time in repeated samples…so perhaps we need to change our opinion.
Can i interpret a hyp-test that way? Or do i have a misconception?
February 12, 2019 at 8:25 pm
The short answer is that, yes, you can draw the interval around the sample mean instead. And, that is, in fact, how you construct confidence intervals. The distance around the null hypothesis for hypothesis tests and the distance around the sample for confidence intervals are the same distance, which is why the results will always agree as long as you use corresponding alpha levels and confidence levels (e.g., alpha 0.05 with a 95% confidence level). I write about how this works in a post about confidence intervals .
I prefer confidence intervals for a number of reasons. They’ll indicate whether you have significant results if they exclude the null value and they indicate the precision of the effect size estimate. Corresponding with what you’re saying, it’s easier to gauge how far a confidence interval is from the null value (often zero) whereas a p-value doesn’t provide that information. See Practical versus Statistical Significance .
So, you don’t have any misconception at all! Just refer to it as a confidence interval rather than a hypothesis test, but, of course, they are very closely related.
January 9, 2019 at 10:37 pm
Hi Jim, Nice Article.. I have a question… I read the Central limit theorem article before this article…
Coming to this article, During almost every hypothesis test, we draw a normal distribution curve assuming there is a sampling distribution (and then we go for test statistic, p value etc…). Do we draw a normal distribution curve for hypo tests because of the central limit theorem…
Thanks in advance, Surya
January 10, 2019 at 1:57 am
These distributions are actually the t-distribution which are different from the normal distribution. T-distributions only have one parameter–the degrees of freedom. As the DF of increases, the t-distribution tightens up. Around 25 degrees of freedom, the t-distribution approximates the normal distribution. Depending on the type of t-test, this corresponds to a sample size of 26 or 27. Similarly, the sampling distribution of the means also approximate the normal distribution at around these sample sizes. With a large enough sample size, both the t-distribution and the sample distribution converge to a normal distribution regardless (largely) of the underlying population distribution. So, yes, the central limit theorem plays a strong role in this.
It’s more accurate to say that central limit theorem causes the sampling distribution of the means to converge on the same distribution that the t-test uses, which allows you to assume that the test produces valid results. But, technically, the t-test is based on the t-distribution.
Problems can occur if the underlying distribution is non-normal and you have a small sample size. In that case, the sampling distribution of the means won’t approximate the t-distribution that the t-test uses. However, the test results will assume that it does and produce results based on that–which is why it causes problems!
November 19, 2018 at 9:15 am
Dear Jim! Thank you very much for your explanation. I need your help to understand my data. I have two samples (about 300 observations) with biased distributions. I did the ttest and obtained the p-value, which is quite small. Can I draw the conclusion that the effect size is small even when the distribution of my data is not normal? Thank you
November 19, 2018 at 9:34 am
Hi Tetyana,
First, when you say that your p-value is small and that you want to “draw the conclusion that the effect size is small,” I assume that you mean statistically significant. When the p-value is low, the null hypothesis must go! In other words, you reject the null and conclude that there is a statistically significant effect–not a small effect.
Now, back to the question at hand! Yes, When you have a sufficiently large sample-size, t-tests are robust to departures from normality. For a 2-sample t-test, you should have at least 15 samples per group, which you exceed by quite a bit. So, yes, you can reliably conclude that your results are statistically significant!
You can thank the central limit theorem! 🙂
September 10, 2018 at 12:18 am
Hello Jim, I am very sorry; I have very elementary of knowledge of stats. So, would you please explain how you got a p- value of 0.03112 in the above calculation/t-test? By looking at a chart? Would you also explain how you got the information that “you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true”?
July 6, 2018 at 7:02 am
A quick question regarding your use of two-tailed critical regions in the article above: why? I mean, what is a real-world scenario that would warrant a two-tailed test of any kind (z, t, etc.)? And if there are none, why keep using the two-tailed scenario as an example, instead of the one-tailed which is both more intuitive and applicable to most if not all practical situations. Just curious, as one person attempting to educate people on stats to another (my take on the one vs. two-tailed tests can be seen here: http://blog.analytics-toolkit.com/2017/one-tailed-two-tailed-tests-significance-ab-testing/ )
Thanks, Georgi
July 6, 2018 at 12:05 pm
There’s the appropriate time and place for both one-tailed and two-tailed tests. I plan to write a post on this issue specifically, so I’ll keep my comments here brief.
So much of statistics is context sensitive. People often want concrete rules for how to do things in statistics but that’s often hard to provide because the answer depends on the context, goals, etc. The question of whether to use a one-tailed or two-tailed test falls firmly in this category of it depends.
I did read the article you wrote. I’ll say that I can see how in the context of A/B testing specifically there might be a propensity to use one-tailed tests. You only care about improvements. There’s probably not too much downside in only caring about one direction. In fact, in a post where I compare different tests and different options , I suggest using a one-tailed test for a similar type of casing involving defects. So, I’m onboard with the idea of using one-tailed tests when they’re appropriate. However, I do think that two-tailed tests should be considered the default choice and that you need good reasons to move to a one-tailed test. Again, your A/B testing area might supply those reasons on a regular basis, but I can’t make that a blanket statement for all research areas.
I think your article mischaracterizes some of the pros and cons of both types of tests. Just a couple of for instances. In a two-tailed test, you don’t have to take the same action regardless of which direction the results are significant (example below). And, yes, you can determine the direction of the effect in a two-tailed test. You simply look at the estimated effect. Is it positive or negative?
On the other hand, I do agree that one-tailed tests don’t increase the overall Type I error. However, there is a big caveat for that. In a two-tailed test, the Type I error rate is evenly split in both tails. For a one-tailed test, the overall Type I error rate does not change, but the Type I errors are redistributed so they all occur in the direction that you are interested in rather than being split between the positive and negative directions. In other words, you’ll have twice as many Type I errors in the specific direction that you’re interested in. That’s not good.
My big concerns with one-tailed tests are that it makes it easier to obtain the results that you want to obtain. And, all of the Type I errors (false positives) are in that direction too. It’s just not a good combination.
To answer your question about when you might want to use two-tailed tests, there are plenty of reasons. For one, you might want to avoid the situation I describe above. Additionally, in a lot of scientific research, the researchers truly are interested in detecting effects in either direction for the sake of science. Even in cases with a practical application, you might want to learn about effects in either direction.
For example, I was involved in a research study that looked at the effects of an exercise intervention on bone density. The idea was that it might be a good way to prevent osteoporosis. I used a two-tailed test. Obviously, we’re hoping that there was positive effect. However, we’d be very interested in knowing whether there was a negative effect too. And, this illustrates how you can have different actions based on both directions. If there was a positive effect, you can recommend that as a good approach and try to promote its use. If there’s a negative effect, you’d issue a warning to not do that intervention. You have the potential for learning both what is good and what is bad. The extra false-positives would’ve cause problems because we’d think that there’d be health benefits for participants when those benefits don’t actually exist. Also, if we had performed only a one-tailed test and didn’t obtain significant results, we’d learn that it wasn’t a positive effect, but we would not know whether it was actually detrimental or not.
Here’s when I’d say it’s OK to use a one-tailed test. Consider a one-tailed test when you’re in situation where you truly only need to know whether an effect exists in one direction, and the extra Type I errors in that direction are an acceptable risk (false positives don’t cause problems), and there’s no benefit in determining whether an effect exists in the other direction. Those conditions really restrict when one-tailed tests are the best choice. Again, those restrictions might not be relevant for your specific field, but as for the usage of statistics as a whole, they’re absolutely crucial to consider.
On the other hand, according to this article, two-tailed tests might be important in A/B testing !
March 30, 2018 at 5:29 am
Dear Sir, please confirm if there is an inadvertent mistake in interpretation as, “We can conclude that mean fuel expenditures have increased since last year.” Our null hypothesis is =260. If found significant, it implies two possibilities – both increase and decrease. Please let us know if we are mistaken here. Many Thanks!
March 30, 2018 at 9:59 am
Hi Khalid, the null hypothesis as it is defined for this test represents the mean monthly expenditure for the previous year (260). The mean expenditure for the current year is 330.6 whereas it was 260 for the previous year. Consequently, the mean has increased from 260 to 330.7 over the course of a year. The p-value indicates that this increase is statistically significant. This finding does not suggest both an increase and a decrease–just an increase. Keep in mind that a significant result prompts us to reject the null hypothesis. So, we reject the null that the mean equals 260.
Let’s explore the other possible findings to be sure that this makes sense. Suppose the sample mean had been closer to 260 and the p-value was greater than the significance level, those results would indicate that the results were not statistically significant. The conclusion that we’d draw is that we have insufficient evidence to conclude that mean fuel expenditures have changed since the previous year.
If the sample mean was less than the null hypothesis (260) and if the p-value is statistically significant, we’d concluded that mean fuel expenditures have decreased and that this decrease is statistically significant.
When you interpret the results, you have to be sure to understand what the null hypothesis represents. In this case, it represents the mean monthly expenditure for the previous year and we’re comparing this year’s mean to it–hence our sample suggests an increase.
Comments and Questions Cancel reply
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null & Alternative Hypotheses | Definitions, Templates & Examples
Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis ( H 0 ): There’s no effect in the population .
- Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:
- The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
- The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question.
- They both make claims about the population.
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
General template sentences
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
- Alternative hypothesis ( H a ): Independent variable affects dependent variable.
Test-specific template sentences
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved October 16, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/
Is this article helpful?

Shaun Turney
Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.
Hypothesis Testing: P-Value Range for Two-Tailed Test

IMAGES
VIDEO
COMMENTS
The p value gets smaller as the test statistic calculated from your data gets further away from the range of test statistics predicted by the null hypothesis. The p value is a proportion: if your p value is 0.05, that means that 5% of the time you would see a test statistic at least as extreme as the one you found if the null hypothesis was ...
S.3.2 Hypothesis Testing (P-Value Approach) The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or ...
Null hypothesis value: 260; Let's work through the step-by-step process of how to calculate a p-value. First, we need to identify the correct test statistic. Because we're comparing one mean to a null value, we need to use a 1-sample t-test. Hence, the t-value is our test statistic, and the t-distribution is our sampling distribution.
Here is the technical definition of P values: P values are the probability of observing a sample statistic that is at least as extreme as your sample statistic when you assume that the null hypothesis is true. Let's go back to our hypothetical medication study. Suppose the hypothesis test generates a P value of 0.03.
In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.
In null-hypothesis significance testing, the -value [note 1] is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. [2] [3] A very small p-value means that such an extreme observed outcome would be very unlikely under the null hypothesis.Even though reporting p-values of statistical tests is ...
A p value is used in hypothesis testing to help you support or reject the null hypothesis. The p value is the evidence against a null hypothesis. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis. P values are expressed as decimals although it may be easier to understand what they are if you convert ...
Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. ... Null values are sometimes used ...
Report exact p-values: Instead of just stating p < 0.05 or p > 0.05, report the exact p-value (e.g., p = 0.032). This provides more information and allows readers to make their own judgments about the strength of evidence. Consider replication and meta-analysis: Single studies, even with very low p-values, can be misleading. Look for replicated ...
The p-value, or probability value, is a statistical measure used in hypothesis testing to assess the strength of evidence against a null hypothesis. It represents the probability of obtaining results as extreme as, or more extreme than, the observed results under the assumption that the null hypothesis is true.
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis. ... R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods, 5(2), 241. Rozeboom, W. W. (1960). The fallacy of the ...
Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample.It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true!. More intuitively, p-value answers the question: Assuming that I live in a world where the null hypothesis holds, how probable is ...
In statistical hypothesis testing, a p-value is a crucial concept that helps researchers quantify the strength of evidence against the null hypothesis. The p-value is defined as the probability of obtaining test results at least as extreme as the observed results, assuming that the null hypothesis is true. This definition highlights the ...
In hypothesis testing, that situation is the assumption that the null hypothesis value is the correct value, or that there is no effect. The value laid out in H0 is our condition under which we interpret our results. To reject this assumption, and thereby reject the null hypothesis, we need results that would be very unlikely if the null was true.
The textbook definition of a p-value is: A p-value is the probability of observing a sample statistic that is at least as extreme as your sample statistic, given that the null hypothesis is true. For example, suppose a factory claims that they produce tires that have a mean weight of 200 pounds. An auditor hypothesizes that the true mean weight ...
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
Using P values and Significance Levels Together. If your P value is less than or equal to your alpha level, reject the null hypothesis. The P value results are consistent with our graphical representation. The P value of 0.03112 is significant at the alpha level of 0.05 but not 0.01.
Here are five essential tips for ensuring the p-value from a hypothesis test is understood correctly. 1. Know What the P-value Represents. First, it is essential to understand what a p-value is. In hypothesis testing, the p-value is defined as the probability of observing your data, or data more extreme, if the null hypothesis is true.
The null hypothesis (H0) answers "No, there's no effect in the population.". The alternative hypothesis (Ha) answers "Yes, there is an effect in the population.". The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
The null hypothesis is the hypothesis that no effect exists in the phenomenon being studied. [36] For the null hypothesis to be rejected, an observed result has to be statistically significant, i.e. the observed p-value is less than the pre-specified significance level .
Answer Explanation Correct answer: Fail to reject the null hypothesis. The conclusion of the hypothesis test is that there is insufficient evidence to suggest that the population mean rate of return for Zoe is greater than the population mean rate of return for Brayden. Compare the p-value that is greater than 0.10 to α=0.05 .