example of data presentation in research

Princeton Correspondents on Undergraduate Research

How to Make a Successful Research Presentation

Turning a research paper into a visual presentation is difficult; there are pitfalls, and navigating the path to a brief, informative presentation takes time and practice. As a TA for  GEO/WRI 201: Methods in Data Analysis & Scientific Writing this past fall, I saw how this process works from an instructor’s standpoint. I’ve presented my own research before, but helping others present theirs taught me a bit more about the process. Here are some tips I learned that may help you with your next research presentation:

More is more

In general, your presentation will always benefit from more practice, more feedback, and more revision. By practicing in front of friends, you can get comfortable with presenting your work while receiving feedback. It is hard to know how to revise your presentation if you never practice. If you are presenting to a general audience, getting feedback from someone outside of your discipline is crucial. Terms and ideas that seem intuitive to you may be completely foreign to someone else, and your well-crafted presentation could fall flat.

Less is more

Limit the scope of your presentation, the number of slides, and the text on each slide. In my experience, text works well for organizing slides, orienting the audience to key terms, and annotating important figures–not for explaining complex ideas. Having fewer slides is usually better as well. In general, about one slide per minute of presentation is an appropriate budget. Too many slides is usually a sign that your topic is too broad.

Limit the scope of your presentation

Don’t present your paper. Presentations are usually around 10 min long. You will not have time to explain all of the research you did in a semester (or a year!) in such a short span of time. Instead, focus on the highlight(s). Identify a single compelling research question which your work addressed, and craft a succinct but complete narrative around it.

You will not have time to explain all of the research you did. Instead, focus on the highlights. Identify a single compelling research question which your work addressed, and craft a succinct but complete narrative around it.

Craft a compelling research narrative

After identifying the focused research question, walk your audience through your research as if it were a story. Presentations with strong narrative arcs are clear, captivating, and compelling.

• Introduction (exposition — rising action)

Orient the audience and draw them in by demonstrating the relevance and importance of your research story with strong global motive. Provide them with the necessary vocabulary and background knowledge to understand the plot of your story. Introduce the key studies (characters) relevant in your story and build tension and conflict with scholarly and data motive. By the end of your introduction, your audience should clearly understand your research question and be dying to know how you resolve the tension built through motive.

• Methods (rising action)

The methods section should transition smoothly and logically from the introduction. Beware of presenting your methods in a boring, arc-killing, ‘this is what I did.’ Focus on the details that set your story apart from the stories other people have already told. Keep the audience interested by clearly motivating your decisions based on your original research question or the tension built in your introduction.

• Results (climax)

Less is usually more here. Only present results which are clearly related to the focused research question you are presenting. Make sure you explain the results clearly so that your audience understands what your research found. This is the peak of tension in your narrative arc, so don’t undercut it by quickly clicking through to your discussion.

• Discussion (falling action)

By now your audience should be dying for a satisfying resolution. Here is where you contextualize your results and begin resolving the tension between past research. Be thorough. If you have too many conflicts left unresolved, or you don’t have enough time to present all of the resolutions, you probably need to further narrow the scope of your presentation.

• Conclusion (denouement)

Return back to your initial research question and motive, resolving any final conflicts and tying up loose ends. Leave the audience with a clear resolution of your focus research question, and use unresolved tension to set up potential sequels (i.e. further research).

Use your medium to enhance the narrative

Visual presentations should be dominated by clear, intentional graphics. Subtle animation in key moments (usually during the results or discussion) can add drama to the narrative arc and make conflict resolutions more satisfying. You are narrating a story written in images, videos, cartoons, and graphs. While your paper is mostly text, with graphics to highlight crucial points, your slides should be the opposite. Adapting to the new medium may require you to create or acquire far more graphics than you included in your paper, but it is necessary to create an engaging presentation.

The most important thing you can do for your presentation is to practice and revise. Bother your friends, your roommates, TAs–anybody who will sit down and listen to your work. Beyond that, think about presentations you have found compelling and try to incorporate some of those elements into your own. Remember you want your work to be comprehensible; you aren’t creating experts in 10 minutes. Above all, try to stay passionate about what you did and why. You put the time in, so show your audience that it’s worth it.

For more insight into research presentations, check out these past PCUR posts written by Emma and Ellie .

— Alec Getraer, Natural Sciences Correspondent

Share this:

• Share on Tumblr

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Quantitative Data Analysis

9 Presenting the Results of Quantitative Analysis

Mikaila Mariel Lemonik Arthur

This chapter provides an overview of how to present the results of quantitative analysis, in particular how to create effective tables for displaying quantitative results and how to write quantitative research papers that effectively communicate the methods used and findings of quantitative analysis.

Writing the Quantitative Paper

Standard quantitative social science papers follow a specific format. They begin with a title page that includes a descriptive title, the author(s)’ name(s), and a 100 to 200 word abstract that summarizes the paper. Next is an introduction that makes clear the paper’s research question, details why this question is important, and previews what the paper will do. After that comes a literature review, which ends with a summary of the research question(s) and/or hypotheses. A methods section, which explains the source of data, sample, and variables and quantitative techniques used, follows. Many analysts will include a short discussion of their descriptive statistics in the methods section. A findings section details the findings of the analysis, supported by a variety of tables, and in some cases graphs, all of which are explained in the text. Some quantitative papers, especially those using more complex techniques, will include equations. Many papers follow the findings section with a discussion section, which provides an interpretation of the results in light of both the prior literature and theory presented in the literature review and the research questions/hypotheses. A conclusion ends the body of the paper. This conclusion should summarize the findings, answering the research questions and stating whether any hypotheses were supported, partially supported, or not supported. Limitations of the research are detailed. Papers typically include suggestions for future research, and where relevant, some papers include policy implications. After the body of the paper comes the works cited; some papers also have an Appendix that includes additional tables and figures that did not fit into the body of the paper or additional methodological details. While this basic format is similar for papers regardless of the type of data they utilize, there are specific concerns relating to quantitative research in terms of the methods and findings that will be discussed here.

In the methods section, researchers clearly describe the methods they used to obtain and analyze the data for their research. When relying on data collected specifically for a given paper, researchers will need to discuss the sample and data collection; in most cases, though, quantitative research relies on pre-existing datasets. In these cases, researchers need to provide information about the dataset, including the source of the data, the time it was collected, the population, and the sample size. Regardless of the source of the data, researchers need to be clear about which variables they are using in their research and any transformations or manipulations of those variables. They also need to explain the specific quantitative techniques that they are using in their analysis; if different techniques are used to test different hypotheses, this should be made clear. In some cases, publications will require that papers be submitted along with any code that was used to produce the analysis (in SPSS terms, the syntax files), which more advanced researchers will usually have on hand. In many cases, basic descriptive statistics are presented in tabular form and explained within the methods section.

The findings sections of quantitative papers are organized around explaining the results as shown in tables and figures. Not all results are depicted in tables and figures—some minor or null findings will simply be referenced—but tables and figures should be produced for all findings to be discussed at any length. If there are too many tables and figures, some can be moved to an appendix after the body of the text and referred to in the text (e.g. “See Table 12 in Appendix A”).

Discussions of the findings should not simply restate the contents of the table. Rather, they should explain and interpret it for readers, and they should do so in light of the hypothesis or hypotheses that are being tested. Conclusions—discussions of whether the hypothesis or hypotheses are supported or not supported—should wait for the conclusion of the paper.

Creating Effective Tables

When creating tables to display the results of quantitative analysis, the most important goals are to create tables that are clear and concise but that also meet standard conventions in the field. This means, first of all, paring down the volume of information produced in the statistical output to just include the information most necessary for interpreting the results, but doing so in keeping with standard table conventions. It also means making tables that are well-formatted and designed, so that readers can understand what the tables are saying without struggling to find information. For example, tables (as well as figures such as graphs) need clear captions; they are typically numbered and referred to by number in the text. Columns and rows should have clear headings. Depending on the content of the table, formatting tools may need to be used to set off header rows/columns and/or total rows/columns; cell-merging tools may be necessary; and shading may be important in tables with many rows or columns.

Here, you will find some instructions for creating tables of results from descriptive, crosstabulation, correlation, and regression analysis that are clear, concise, and meet normal standards for data display in social science. In addition, after the instructions for creating tables, you will find an example of how a paper incorporating each table might describe that table in the text.

Descriptive Statistics

When presenting the results of descriptive statistics, we create one table with columns for each type of descriptive statistic and rows for each variable. Note, of course, that depending on level of measurement only certain descriptive statistics are appropriate for a given variable, so there may be many cells in the table marked with an — to show that this statistic is not calculated for this variable. So, consider the set of descriptive statistics below, for occupational prestige, age, highest degree earned, and whether the respondent was born in this country.

To display these descriptive statistics in a paper, one might create a table like Table 2. Note that for discrete variables, we use the value label in the table, not the value.

If we were then to discuss our descriptive statistics in a quantitative paper, we might write something like this (note that we do not need to repeat every single detail from the table, as readers can peruse the table themselves):

This analysis relies on four variables from the 2021 General Social Survey: occupational prestige score, age, highest degree earned, and whether the respondent was born in the United States. Descriptive statistics for all four variables are shown in Table 2. The median occupational prestige score is 47, with a range from 16 to 80. 50% of respondents had occupational prestige scores scores between 35 and 59. The median age of respondents is 53, with a range from 18 to 89. 50% of respondents are between ages 37 and 66. Both variables have little skew. Highest degree earned ranges from less than high school to a graduate degree; the median respondent has earned an associate’s degree, while the modal response (given by 39.8% of the respondents) is a high school degree. 88.8% of respondents were born in the United States.

Crosstabulation

When presenting the results of a crosstabulation, we simplify the table so that it highlights the most important information—the column percentages—and include the significance and association below the table. Consider the SPSS output below.

Table 4 shows how a table suitable for include in a paper might look if created from the SPSS output in Table 3. Note that we use asterisks to indicate the significance level of the results: * means p < 0.05; ** means p < 0.01; *** means p < 0.001; and no stars mean p > 0.05 (and thus that the result is not significant). Also note than N is the abbreviation for the number of respondents.

If we were going to discuss the results of this crosstabulation in a quantitative research paper, the discussion might look like this:

A crosstabulation of respondent’s class identification and their highest degree earned, with class identification as the independent variable, is significant, with a Spearman correlation of 0.419, as shown in Table 4. Among lower class and working class respondents, more than 50% had earned a high school degree. Less than 20% of poor respondents and less than 40% of working-class respondents had earned more than a high school degree. In contrast, the majority of middle class and upper class respondents had earned at least a bachelor’s degree. In fact, 50% of upper class respondents had earned a graduate degree.

Correlation

When presenting a correlating matrix, one of the most important things to note is that we only present half the table so as not to include duplicated results. Think of the line through the table where empty cells exist to represent the correlation between a variable and itself, and include only the triangle of data either above or below that line of cells. Consider the output in Table 5.

Table 6 shows what the contents of Table 5 might look like when a table is constructed in a fashion suitable for publication.

If we were to discuss the results of this bivariate correlation analysis in a quantitative paper, the discussion might look like this:

Bivariate correlations were run among variables measuring age, occupational prestige, the highest year of school respondents completed, and family income in constant 1986 dollars, as shown in Table 6. Correlations between age and highest year of school completed and between age and family income are not significant. All other correlations are positive and significant at the p<0.001 level. The correlation between age and occupational prestige is weak; the correlations between income and occupational prestige and between income and educational attainment are moderate, and the correlation between education and occupational prestige is strong.

To present the results of a regression, we create one table that includes all of the key information from the multiple tables of SPSS output. This includes the R 2 and significance of the regression, either the B or the beta values (different analysts have different preferences here) for each variable, and the standard error and significance of each variable. Consider the SPSS output in Table 7.

The regression output in shown in Table 7 contains a lot of information. We do not include all of this information when making tables suitable for publication. As can be seen in Table 8, we include the Beta (or the B), the standard error, and the significance asterisk for each variable; the R 2 and significance for the overall regression; the degrees of freedom (which tells readers the sample size or N); and the constant; along with the key to p/significance values.

If we were to discuss the results of this regression in a quantitative paper, the results might look like this:

Table 8 shows the results of a regression in which age, occupational prestige, and highest year of school completed are the independent variables and family income is the dependent variable. The regression results are significant, and all of the independent variables taken together explain 15.6% of the variance in family income. Age is not a significant predictor of income, while occupational prestige and educational attainment are. Educational attainment has a larger effect on family income than does occupational prestige. For every year of additional education attained, family income goes up on average by $3,988.545; for every one-unit increase in occupational prestige score, family income goes up on average by $522.887. [1]

• Choose two discrete variables and three continuous variables from a dataset of your choice. Produce appropriate descriptive statistics on all five of the variables and create a table of the results suitable for inclusion in a paper.
• Using the two discrete variables you have chosen, produce an appropriate crosstabulation, with significance and measure of association. Create a table of the results suitable for inclusion in a paper.
• Using the three continuous variables you have chosen, produce a correlation matrix. Create a table of the results suitable for inclusion in a paper.
• Using the three continuous variables you have chosen, produce a multivariate linear regression. Create a table of the results suitable for inclusion in a paper.
• Write a methods section describing the dataset, analytical methods, and variables you utilized in questions 1, 2, 3, and 4 and explaining the results of your descriptive analysis.
• Write a findings section explaining the results of the analyses you performed in questions 2, 3, and 4.
• Note that the actual numberical increase comes from the B values, which are shown in the SPSS output in Table 7 but not in the reformatted Table 8. ↵

Social Data Analysis Copyright © 2021 by Mikaila Mariel Lemonik Arthur is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Presenting data in tables and charts *

Rodrigo pereira duquia, joão luiz bastos, renan rangel bonamigo, david alejandro gonzález-chica, jeovany martínez-mesa.

• Author information
• Article notes
• Copyright and License information

MAILING ADDRESS: Rodrigo Pereira Duquia, R. Independência, 172 - sala 902 90035-070 - Independência - RS, Brazil. E-mail: [email protected]

Received 2013 Dec 2; Accepted 2014 Feb 2.

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

The present paper aims to provide basic guidelines to present epidemiological data using tables and graphs in Dermatology. Although simple, the preparation of tables and graphs should follow basic recommendations, which make it much easier to understand the data under analysis and to promote accurate communication in science. Additionally, this paper deals with other basic concepts in epidemiology, such as variable, observation, and data, which are useful both in the exchange of information between researchers and in the planning and conception of a research project.

Keywords: Epidemiology; Epidemiology, descriptive; Tables

INTRODUCTION

Among the essential stages of epidemiological research, one of the most important is the identification of data with which the researcher is working, as well as a clear and synthetic description of these data using graphs and tables. The identification of the type of data has an impact on the different stages of the research process, encompassing the research planning and the production/publication of its results. For example, the use of a certain type of data impacts the amount of time it will take to collect the desired information (throughout the field work) and the selection of the most appropriate statistical tests for data analysis.

On the other hand, the preparation of tables and graphs is a crucial tool in the analysis and production/publication of results, given that it organizes the collected information in a clear and summarized fashion. The correct preparation of tables allows researchers to present information about tens or hundreds of individuals efficiently and with significant visual appeal, making the results more easily understandable and thus more attractive to the users of the produced information. Therefore, it is very important for the authors of scientific articles to master the preparation of tables and graphs, which requires previous knowledge of data characteristics and the ability of identifying which type of table or graph is the most appropriate for the situation of interest.

BASIC CONCEPTS

Before evaluating the different types of data that permeate an epidemiological study, it is worth discussing about some key concepts (herein named data, variables and observations):

Data - during field work, researchers collect information by means of questions, systematic observations, and imaging or laboratory tests. All this gathered information represents the data of the research. For example, it is possible to determine the color of an individual's skin according to Fitzpatrick classification or quantify the number of times a person uses sunscreen during summer. 1 , 2 All the information collected during research is generically named "data." A set of individual data makes it possible to perform statistical analysis. If the quality of data is good, i.e., if the way information was gathered was appropriate, the next stages of database preparation, which will set the ground for analysis and presentation of results, will be properly conducted.

Observations - are measurements carried out in one or more individuals, based on one or more variables. For instance, if one is working with the variable "sex" in a sample of 20 individuals and knows the exact amount of men and women in this sample (10 for each group), it can be said that this variable has 20 observations.

Variables - are constituted by data. For instance, an individual may be male or female. In this case, there are 10 observations for each sex, but "sex" is the variable that is referred to as a whole. Another example of variable is "age" in complete years, in which observations are the values 1 year, 2 years, 3 years, and so forth. In other words, variables are characteristics or attributes that can be measured, assuming different values, such as sex, skin type, eye color, age of the individuals under study, laboratory results, or the presence of a given lesion/disease. Variables are specifically divided into two large groups: (a) the group of categorical or qualitative variables, which is subdivided into dichotomous, nominal and ordinal variables; and (b) the group of numerical or quantitative variables, which is subdivided into continuous and discrete variables.

Categorical variables

Dichotomous variables, also known as binary variables: are those that have only two categories, i.e., only two response options. Typical examples of this type of variable are sex (male and female) and presence of skin cancer (yes or no).

Ordinal variables: are those that have three or more categories with an obvious ordering of the categories (whether in an ascending or descending order). For example, Fitzpatrick skin classification into types I, II, III, IV and V. 1

Nominal variables: are those that have three or more categories with no apparent ordering of the categories. Example: blood types A, B, AB, and O, or brown, blue or green eye colors.

Numerical variables

Discrete variables: are observations that can only take certain numerical values. An example of this type of variable is subjects' age, when assessed in complete years of life (1 year, 2 years, 3 years, 4 years, etc.) and the number of times a set of patients visited the dermatologist in a year.

Continuous variables: are those measured on a continuous scale, i.e., which have as many decimal places as the measuring instrument can record. For instance: blood pressure, birth weight, height, or even age, when measured on a continuous scale.

It is important to point out that, depending on the objectives of the study, data may be collected as discrete or continuous variables and be subsequently transformed into categorical variables to suit the purpose of the research and/or make interpretation easier. However, it is important to emphasize that variables measured on a numerical scale (whether discrete or continuous) are richer in information and should be preferred for statistical analyses. Figure 1 shows a diagram that makes it easier to understand, identify and classify the abovementioned variables.

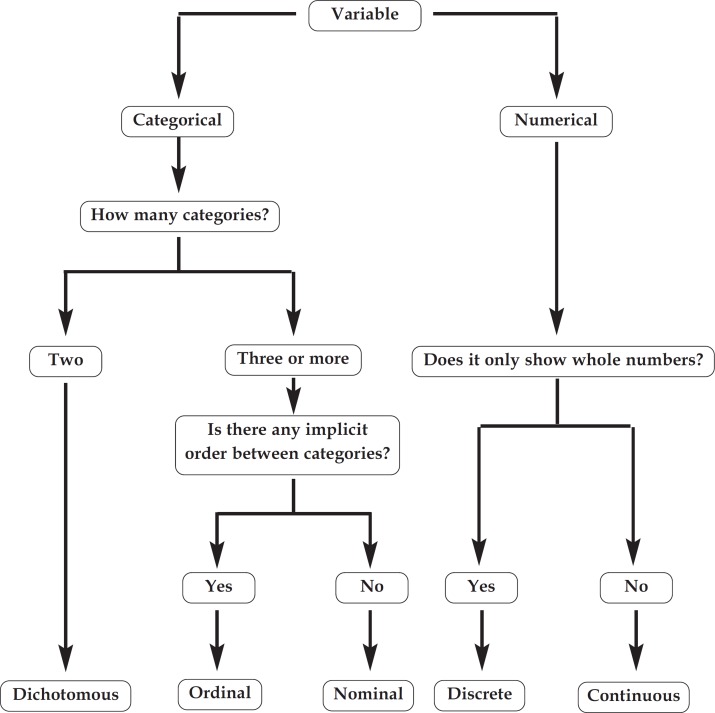
Types of variables

DATA PRESENTATION IN TABLES AND GRAPHS

Firstly, it is worth emphasizing that every table or graph should be self-explanatory, i.e., should be understandable without the need to read the text that refers to it refers.

Presentation of categorical variables

In order to analyze the distribution of a variable, data should be organized according to the occurrence of different results in each category. As for categorical variables, frequency distributions may be presented in a table or a graph, including bar charts and pie or sector charts. The term frequency distribution has a specific meaning, referring to the the way observations of a given variable behave in terms of its absolute, relative or cumulative frequencies.

In order to synthesize information contained in a categorical variable using a table, it is important to count the number of observations in each category of the variable, thus obtaining its absolute frequencies. However, in addition to absolute frequencies, it is worth presenting its percentage values, also known as relative frequencies. For example, table 1 expresses, in absolute and relative terms, the frequency of acne scars in 18-year-old youngsters from a population-based study conducted in the city of Pelotas, Southern Brazil, in 2010. 3

Absolute and relative frequencies of acne scar in 18- year-old adolescents (n = 2.414). Pelotas, Brazil, 2010

The same information from table 1 may be presented as a bar or a pie chart, which can be prepared considering the absolute or relative frequency of the categories. Figures 2 and 3 illustrate the same information shown in table 1 , but present it as a bar chart and a pie chart, respectively. It can be observed that, regardless of the form of presentation, the total number of observations must be mentioned, whether in the title or as part of the table or figure. Additionally, appropriate legends should always be included, allowing for the proper identification of each of the categories of the variable and including the type of information provided (absolute and/or relative frequency).

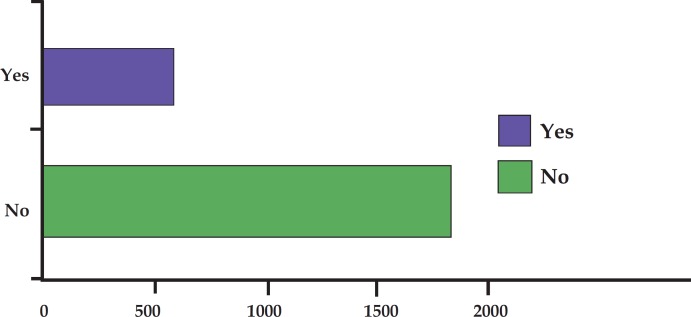
Absolute frequencies of acne scar in 18-year-old adolescents (n = 2.414). Pelotas, Brazil, 2010

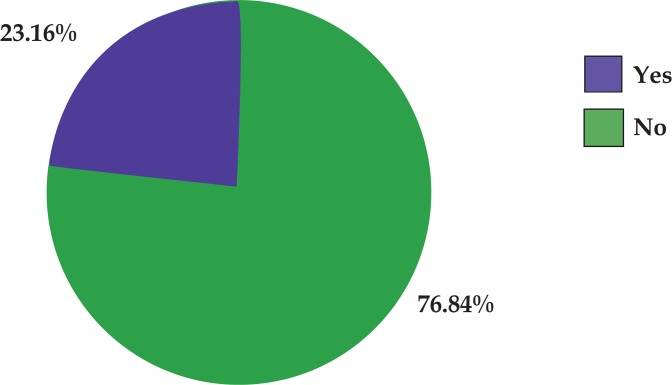
Relative frequencies of acne scar in 18-year-old adolescents (n = 2.414). Pelotas, Brazil, 2010

Presentation of numerical variables

Frequency distributions of numerical variables can be displayed in a table, a histogram chart, or a frequency polygon chart. With regard to discrete variables, it is possible to present the number of observations according to the different values found in the study, as illustrated in table 2 . This type of table may provide a wide range of information on the collected data.

Educational level of 18-year-old adolescents (n = 2,199). Pelotas, Brazil, 2010

Table 2 shows the distribution of educational levels among 18-year-old youngsters from Pelotas, Southern Brazil, with absolute, relative, and cumulative relative frequencies. In this case, absolute and relative frequencies correspond to the absolute number and the percentage of individuals according to their distribution for this variable, respectively, based on complete years of education. It should be noticed that there are 450 adolescents with 8 years of education, which corresponds to 20.5% of the subjects. Tables may also present the cumulative relative frequency of the variable. In this case, it was found that 50.6% of study subjects have up to 8 years of education. It is important to point that, although the same data were used, each form of presentation (absolute, relative or cumulative frequency) provides different information and may be used to understand frequency distribution from different perspectives.

When one wants to evaluate the frequency distribution of continuous variables using tables or graphs, it is necessary to transform the variable into categories, preferably creating categories with the same size (or the same amplitude). However, in addition to this general recommendation, other basic guidelines should be followed, such as: (1) subtracting the highest from the lowest value for the variable of interest; (2) dividing the result of this subtraction by the number of categories to be created (usually from three to ten); and (3) defining category intervals based on this last result.

For example, in order to categorize height (in meters) of a set of individuals, the first step is to identify the tallest and the shortest individual of the sample. Let us assume that the tallest individual is 1.85m tall and the shortest, 1.55m tall, with a difference of 0.3m between these values. The next step is to divide this difference by the number of categories to be created, e.g., five. Thus, 0.3m divided by five equals 0.06m, which means that categories will have exactly this range and will be numerically represented by the following range of values: 1st category - 1.55m to 1.60m; 2nd category - 1.61m to 1.66m; 3rd category - 1.67m to 1.72m; 4th category - 1.73m to 1.78m; 5th category - 1.79m to 1.85m.

Table 3 illustrates weight values at 18 years of age in kg (continuous numerical variable) obtained in a study with youngsters from Pelotas, Southern Brazil. 4 , 5 Figure 4 shows a histogram with the variable weight categorized into 20-kg intervals. Therefore, it is possible to observe that data from continuous numerical variables may be presented in tables or graphs.

Weight distribution among 18-year-old young male sex (n = 2.194). Pelotas, Brazil, 2010

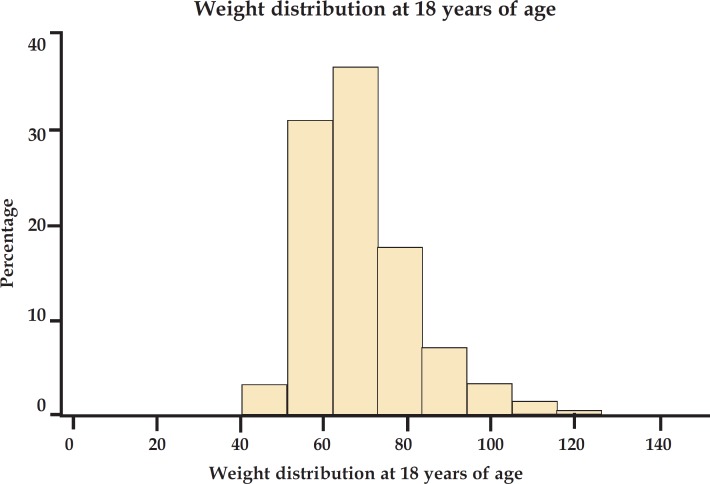
Weight distribution at 18 years of age among youngsters from the city of Pelotas. Pelotas (n = 2.194), Brazil, 2010

Assessing the relationship between two variables

The forms of data presentation that have been described up to this point illustrated the distribution of a given variable, whether categorical or numerical. In addition, it is possible to present the relationship between two variables of interest, either categorical or numerical.

The relationship between categorical variables may be investigated using a contingency table, which has the purpose of analyzing the association between two or more variables. The lines of this type of table usually display the exposure variable (independent variable), and the columns, the outcome variable (dependent variable). For example, in order to study the effect of sun exposure (exposure variable) on the development of skin cancer (outcome variable), it is possible to place the variable sun exposure on the lines and the variable skin cancer on the columns of a contingency table. Tables may be easier to understand by including total values in lines and columns. These values should agree with the sum of the lines and/or columns, as appropriate, whereas relative values should be in accordance with the exposure variable, i.e., the sum of the values mentioned in the lines should total 100%.

It is such a display of percentage values that will make it possible for risk or exposure groups to be compared with each other, in order to investigate whether individuals exposed to a given risk factor show higher frequency of the disease of interest. Thus, table 4 shows that 75.0%, 9.0%, and 0.3% of individuals in the study sample who had been working exposed to the sun for 20 years or more, for less than 20 years, and had never been working exposed to the sun, respectively, developed non-melanoma skin cancer. Another way of interpreting this table is observing that 25.0%, 91%,.0%, and 99.7% of individuals who had been working exposed to the sun for 20 years of more, for less than 20 years, and had never been working exposed to the sun did not develop non-melanoma skin cancer. This form of presentation is one of the most used in the literature and makes the table easier to read.

Sun exposure during work and non-melanoma skin cancer (hypothetical data).

The relationship between two numerical variables or between one numerical variable and one categorical variable may be assessed using a scatter diagram, also known as dispersion diagram. In this diagram, each pair of values is represented by a symbol or a dot, whose horizontal and vertical positions are determined by the value of the first and second variables, respectively. By convention, vertical and horizontal axes should correspond to outcome and exposure variables, respectively. Figure 5 shows the relationship between weight and height among 18-year-old youngsters from Pelotas, Southern Brazil, in 2010. 3 , 4 The diagram presented in figure 5 should be interpreted as follows: the increase in subjects' height is accompanied by an increase in their weight.

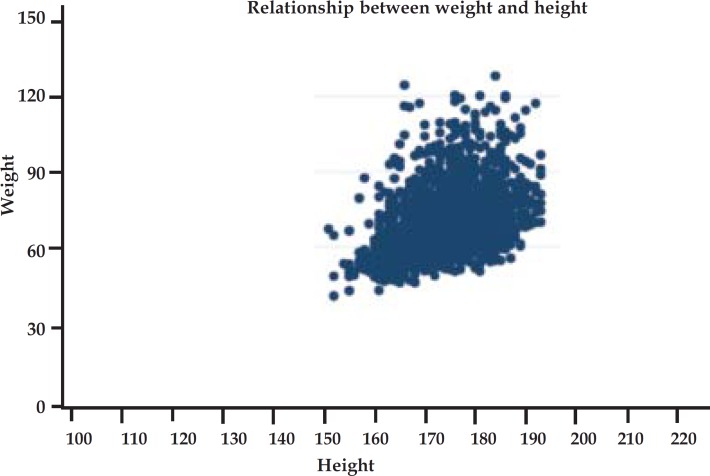
Point diagram for the relationship between weight (kg) and height (cm) among 18-year-old youngsters from the city of Pelotas (n = 2.194). Pelotas, Brazil, 2010.

BASIC RULES FOR THE PREPARATION OF TABLES AND GRAPHS

Ideally, every table should:

Be self-explanatory;

Present values with the same number of decimal places in all its cells (standardization);

Include a title informing what is being described and where, as well as the number of observations (N) and when data were collected;

Have a structure formed by three horizontal lines, defining table heading and the end of the table at its lower border;

Not have vertical lines at its lateral borders;

Provide additional information in table footer, when needed;

Be inserted into a document only after being mentioned in the text; and

Be numbered by Arabic numerals.

Similarly to tables, graphs should:

Include, below the figure, a title providing all relevant information;

Be referred to as figures in the text;

Identify figure axes by the variables under analysis;

Quote the source which provided the data, if required;

Demonstrate the scale being used; and

Be self-explanatory.

The graph's vertical axis should always start with zero. A usual type of distortion is starting this axis with values higher than zero. Whenever it happens, differences between variables are overestimated, as can been seen in figure 6 .

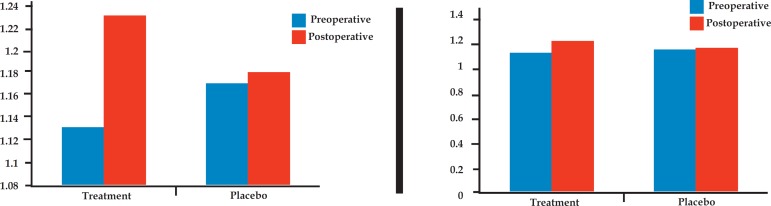
Figure showing how graphs in which the Y-axis does not start with zero tend to overestimate the differences under analysis. On the left there is a graph whose Y axis does not start with zero and on the right a graph reproducing the same data but with the Y axis starting with zero.

Understanding how to classify the different types of variables and how to present them in tables or graphs is an essential stage for epidemiological research in all areas of knowledge, including Dermatology. Mastering this topic collaborates to synthesize research results and prevents the misuse or overuse of tables and figures in scientific papers.

Conflict of Interest: None

Financial Support: None

How to cite this article: Duquia RP, Bastos JL, Bonamigo RR, González-Chica DA, Martínez-Mesa J. Presenting data in tables and charts. An Bras Dermatol. 2014;89(2):280-5.

Work performed at the Dermatology service, Universidade Federal de Ciências da Saúde de Porto Alegre (UFCSPA), Departamento de Saúde Pública e Departamento de Nutrição da UFSC.

• 1. Walker SL, Hawk JLM, Young AR. Acute and chronic effects. In: Freedberg IM, Eisen AZ, Wolff K, Austen KF, Goldsmith LA, Katz SI, editors. Fitzpatrick's Dermatology in General Medicine. 8th ed. pp. 1275–1281. [ Google Scholar ]
• 2. Duquia RP, Baptista Menezes AM, Reichert FF, de Almeida HL., Jr. Prevalence and associated factors with sunscreen use in Southern Brazil: A population-based study. J Am Acad Dermatol. 2007;57:73–80. doi: 10.1016/j.jaad.2007.03.012. [ DOI ] [ PubMed ] [ Google Scholar ]
• 3. Duquia RP, de Almeida HL, Jr., Breunig JA, Souzat PR, Göellner CD. Most common patterns of acne in male adolescents: a population-based study. Int J Dermatol. 2013;52:550–553. doi: 10.1111/j.1365-4632.2011.05333.x. [ DOI ] [ PubMed ] [ Google Scholar ]
• 4. Breunig Jde A, de Almeida HL, Jr., Duquia RP, Souza PR, Staub HL. Scalp seborrheic dermatitis: prevalence and associated factors in male adolescents. Int J Dermatol. 2012;51:46–49. doi: 10.1111/j.1365-4632.2011.04964.x. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Almeida H, Jr., Cecconi J, Duquia RP, Souza PR, Breunig J. Sensitivity and specificity of self-reported acne in 18-year-old adolescent males. Int J Dermatol. 2013;52:946–948. doi: 10.1111/j.1365-4632.2011.05443.x. [ DOI ] [ PubMed ] [ Google Scholar ]
• View on publisher site
• PDF (138.7 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections