limitations of quasi experiments

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

The Limitations of Quasi-Experimental Studies, and Methods for Data Analysis When a Quasi-Experimental Research Design Is Unavoidable

Chittaranjan andrade.

• Author information
• Article notes
• Copyright and License information

Chittaranjan Andrade, Dept. of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bengaluru, Karnataka 560029, India. Email: [email protected]

Issue date 2021 Sep.

This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 License ( https://creativecommons.org/licenses/by-nc/4.0/ ) which permits non-commercial use, reproduction and distribution of the work without further permission provided the original work is attributed as specified on the SAGE and Open Access page ( https://us.sagepub.com/en-us/nam/open-access-at-sage ).

A quasi-experimental (QE) study is one that compares outcomes between intervention groups where, for reasons related to ethics or feasibility, participants are not randomized to their respective interventions; an example is the historical comparison of pregnancy outcomes in women who did versus did not receive antidepressant medication during pregnancy. QE designs are sometimes used in noninterventional research, as well; an example is the comparison of neuropsychological test performance between first degree relatives of schizophrenia patients and healthy controls. In QE studies, groups may differ systematically in several ways at baseline, itself; when these differences influence the outcome of interest, comparing outcomes between groups using univariable methods can generate misleading results. Multivariable regression is therefore suggested as a better approach to data analysis; because the effects of confounding variables can be adjusted for in multivariable regression, the unique effect of the grouping variable can be better understood. However, although multivariable regression is better than univariable analyses, there are inevitably inadequately measured, unmeasured, and unknown confounds that may limit the validity of the conclusions drawn. Investigators should therefore employ QE designs sparingly, and only if no other option is available to answer an important research question.

Keywords: Quasi-experimental study, research design, univariable analysis, multivariable regression, confounding variables

If we wish to study how antidepressant drug treatment affects outcomes in pregnancy, we should ideally randomize depressed pregnant women to receive an antidepressant drug or placebo; this is a randomized controlled trial (RCT) research design. However, because ethics committees are unlikely to approve such RCTs, researchers can only examine pregnancy outcomes (prospectively or retrospectively) in women who did versus did not receive antidepressant drugs; this is a quasi-experimental (QE) research design. A QE study is one that compares outcomes between intervention groups where, for reasons related to ethics or feasibility, participants are not randomized to their respective interventions.

QE studies are problematic because, when participants are not randomized to intervention versus control groups, systematic biases may influence group membership. For example, women who are prescribed and who accept antidepressant medications during pregnancy are likely to be more severely ill than those who are not prescribed or those who do not accept antidepressant medications during pregnancy. So, if adverse pregnancy outcomes are commoner in the antidepressant group, they may be consequences of genetic, physiological, and/or behavioral features that characterize severe depression rather than the antidepressant treatment, itself.

A statistical approach to dealing with such confounds is to perform a regression analysis where pregnancy outcome is the dependent variable and antidepressant treatment, age, sex, socioeconomic status, medical history, family history, smoking history, drinking history, history of use of other substances, nutrition, history of infection during pregnancy, and dozens of other important variables that can influence pregnancy outcomes are independent variables. In such a regression, antidepressant treatment is the independent variable of interest, and the remaining independent variables are confounders that are adjusted for in the regression so that the unique effect of antidepressant treatment on pregnancy outcomes can be better identified. Propensity score matching refines the approach to analysis. 1

Many investigators use QE designs to answer their research questions, though not necessarily as an “experiment” with an intervention. For example, Thomas et al. 2 compared psychosocial dysfunction and family burden between outpatients diagnosed with schizophrenia and those diagnosed with obsessive-compulsive disorder (OCD). Obviously, it is not feasible to randomize patients to have schizophrenia or OCD. So, in their analysis, Thomas et al. 2 first examined whether the two groups were comparable on important sociodemographic and clinical variables. They found that the groups did not differ on, for example, age, family income, and duration of illness (but here, and in other QE studies, as well, these baseline comparisons would almost certainly have been underpowered); however, the schizophrenia group was overrepresented for males and for a history of substance abuse. In further analysis, Thomas et al. 2 used t tests to compare dysfunction and burden between the two groups; they found that both dysfunction and burden were greater in schizophrenia than in OCD.

Now, because patients had not been randomized to their respective diagnoses, it is obvious that the groups could have differed in many ways and not in diagnosis, alone. So, separate regressions should have been conducted with dysfunction and with burden as the dependent variable, and with diagnosis, age, sex, socioeconomic status, duration of illness, history of substance abuse, and others as the independent variables. Such an analysis would allow the investigators to understand not only the unique impact of the diagnosis but also the impact of the other sociodemographic and clinical variables on dysfunction and burden.

Note that inadequately measured, unmeasured, and unknown confounds would still have plagued the results. For example, in this study, 2 severity of illness was an unmeasured confound. What if the authors had, by chance, sampled more severely ill schizophrenia patients and less severely ill OCD patients? Then, illness severity rather than clinical diagnosis would have explained the greater dysfunction and burden observed in the schizophrenia group. Had they obtained a global rating of illness, they could have included it as an additional, important independent variable in the regression.

In another study with a QE design, Harave et al., 3 like Thomas et al., 2 used univariate tests to compare neurocognitive functioning between unaffected first-degree relatives of schizophrenia patients and healthy controls. More correctly, because there are likely to be systematic differences between schizophrenia relatives and healthy controls, they should have performed multivariable regressions with neurocognitive measures as the dependent variables, and with group and confounders as independent variables. Confounders that could have been considered include age, sex, education, family income, a measure of stress, history of smoking, drinking, other substance use, and so on, all of which can directly or indirectly influence neurocognitive performances.

This multivariable regression approach to data analysis in QE designs requires the a priori identification and measurement of all important confounding variables. In such analyses, the sample size for a continuous dependent variable should ideally be at least 10–15 times the number of independent variables. 4 Given that the number of confounding variables to be included is likely to be large, a very large sample will become necessary. Additionally, because studies are never perfect, it would be impossible to adjust for inadequately measured, unmeasured, and unknown confounds (but adjusting for whatever is known and measured is better than making no adjustments, at all). All said and done, the QE research design is best avoided because it is flawed and because even the best statistical approaches to data analysis would be imperfect. The QE design should be considered only when no other options are available. Readers are referred to Harris et al. 5 for a further discussion on QE studies.

Declaration of Conflicting Interests: The author declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding: The author received no financial support for the research, authorship, and/or publication of this article.

• 1. Andrade C. Propensity score matching in nonrandomized studies: A concept simply explained using antidepressant treatment during pregnancy as an example. J Clin Psychiatry, 2017; 78(2): e162–e165. [ DOI ] [ PubMed ] [ Google Scholar ]
• 2. Thomas JK, Suresh Kumar PN, Verma AN, et al. Psychosocial dysfunction and family burden in schizophrenia and obsessive compulsive disorder. Indian J Psychiatry, 2004; 46(3): 238–243. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 3. Harave VS, Shivakumar V, Kalmady SV, et al. Neurocognitive impairments in unaffected first-degree relatives of schizophrenia. Indian J Psychol Med, 2017; 39(3): 250–253. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 4. Babyak MA. What you see may not be what you get: a brief, nontechnical introduction to overfitting in regression-type models. Psychosom Med, 2004; 66(3): 411–421. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Harris AD, McGregor JC, Perencevich EN, et al. The use and interpretation of quasi-experimental studies in medical informatics. J Am Med Inform Assoc, 2006; 13(1): 16–23. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• View on publisher site
• PDF (717.9 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

• Privacy Policy

Home » Quasi-Experimental Research Design – Types, Methods

Quasi-Experimental Research Design – Types, Methods

Table of Contents

Quasi-Experimental Design

Quasi-experimental design is a research method that seeks to evaluate the causal relationships between variables, but without the full control over the independent variable(s) that is available in a true experimental design.

In a quasi-experimental design, the researcher uses an existing group of participants that is not randomly assigned to the experimental and control groups. Instead, the groups are selected based on pre-existing characteristics or conditions, such as age, gender, or the presence of a certain medical condition.

Types of Quasi-Experimental Design

There are several types of quasi-experimental designs that researchers use to study causal relationships between variables. Here are some of the most common types:

Non-Equivalent Control Group Design

This design involves selecting two groups of participants that are similar in every way except for the independent variable(s) that the researcher is testing. One group receives the treatment or intervention being studied, while the other group does not. The two groups are then compared to see if there are any significant differences in the outcomes.

Interrupted Time-Series Design

This design involves collecting data on the dependent variable(s) over a period of time, both before and after an intervention or event. The researcher can then determine whether there was a significant change in the dependent variable(s) following the intervention or event.

Pretest-Posttest Design

This design involves measuring the dependent variable(s) before and after an intervention or event, but without a control group. This design can be useful for determining whether the intervention or event had an effect, but it does not allow for control over other factors that may have influenced the outcomes.

Regression Discontinuity Design

This design involves selecting participants based on a specific cutoff point on a continuous variable, such as a test score. Participants on either side of the cutoff point are then compared to determine whether the intervention or event had an effect.

Natural Experiments

This design involves studying the effects of an intervention or event that occurs naturally, without the researcher’s intervention. For example, a researcher might study the effects of a new law or policy that affects certain groups of people. This design is useful when true experiments are not feasible or ethical.

Data Analysis Methods

Here are some data analysis methods that are commonly used in quasi-experimental designs:

Descriptive Statistics

This method involves summarizing the data collected during a study using measures such as mean, median, mode, range, and standard deviation. Descriptive statistics can help researchers identify trends or patterns in the data, and can also be useful for identifying outliers or anomalies.

Inferential Statistics

This method involves using statistical tests to determine whether the results of a study are statistically significant. Inferential statistics can help researchers make generalizations about a population based on the sample data collected during the study. Common statistical tests used in quasi-experimental designs include t-tests, ANOVA, and regression analysis.

Propensity Score Matching

This method is used to reduce bias in quasi-experimental designs by matching participants in the intervention group with participants in the control group who have similar characteristics. This can help to reduce the impact of confounding variables that may affect the study’s results.

Difference-in-differences Analysis

This method is used to compare the difference in outcomes between two groups over time. Researchers can use this method to determine whether a particular intervention has had an impact on the target population over time.

Interrupted Time Series Analysis

This method is used to examine the impact of an intervention or treatment over time by comparing data collected before and after the intervention or treatment. This method can help researchers determine whether an intervention had a significant impact on the target population.

Regression Discontinuity Analysis

This method is used to compare the outcomes of participants who fall on either side of a predetermined cutoff point. This method can help researchers determine whether an intervention had a significant impact on the target population.

Steps in Quasi-Experimental Design

Here are the general steps involved in conducting a quasi-experimental design:

• Identify the research question: Determine the research question and the variables that will be investigated.
• Choose the design: Choose the appropriate quasi-experimental design to address the research question. Examples include the pretest-posttest design, non-equivalent control group design, regression discontinuity design, and interrupted time series design.
• Select the participants: Select the participants who will be included in the study. Participants should be selected based on specific criteria relevant to the research question.
• Measure the variables: Measure the variables that are relevant to the research question. This may involve using surveys, questionnaires, tests, or other measures.
• Implement the intervention or treatment: Implement the intervention or treatment to the participants in the intervention group. This may involve training, education, counseling, or other interventions.
• Collect data: Collect data on the dependent variable(s) before and after the intervention. Data collection may also include collecting data on other variables that may impact the dependent variable(s).
• Analyze the data: Analyze the data collected to determine whether the intervention had a significant impact on the dependent variable(s).
• Draw conclusions: Draw conclusions about the relationship between the independent and dependent variables. If the results suggest a causal relationship, then appropriate recommendations may be made based on the findings.

Quasi-Experimental Design Examples

Here are some examples of real-time quasi-experimental designs:

• Evaluating the impact of a new teaching method: In this study, a group of students are taught using a new teaching method, while another group is taught using the traditional method. The test scores of both groups are compared before and after the intervention to determine whether the new teaching method had a significant impact on student performance.
• Assessing the effectiveness of a public health campaign: In this study, a public health campaign is launched to promote healthy eating habits among a targeted population. The behavior of the population is compared before and after the campaign to determine whether the intervention had a significant impact on the target behavior.
• Examining the impact of a new medication: In this study, a group of patients is given a new medication, while another group is given a placebo. The outcomes of both groups are compared to determine whether the new medication had a significant impact on the targeted health condition.
• Evaluating the effectiveness of a job training program : In this study, a group of unemployed individuals is enrolled in a job training program, while another group is not enrolled in any program. The employment rates of both groups are compared before and after the intervention to determine whether the training program had a significant impact on the employment rates of the participants.
• Assessing the impact of a new policy : In this study, a new policy is implemented in a particular area, while another area does not have the new policy. The outcomes of both areas are compared before and after the intervention to determine whether the new policy had a significant impact on the targeted behavior or outcome.

Applications of Quasi-Experimental Design

Here are some applications of quasi-experimental design:

• Educational research: Quasi-experimental designs are used to evaluate the effectiveness of educational interventions, such as new teaching methods, technology-based learning, or educational policies.
• Health research: Quasi-experimental designs are used to evaluate the effectiveness of health interventions, such as new medications, public health campaigns, or health policies.
• Social science research: Quasi-experimental designs are used to investigate the impact of social interventions, such as job training programs, welfare policies, or criminal justice programs.
• Business research: Quasi-experimental designs are used to evaluate the impact of business interventions, such as marketing campaigns, new products, or pricing strategies.
• Environmental research: Quasi-experimental designs are used to evaluate the impact of environmental interventions, such as conservation programs, pollution control policies, or renewable energy initiatives.

When to use Quasi-Experimental Design

Here are some situations where quasi-experimental designs may be appropriate:

• When the research question involves investigating the effectiveness of an intervention, policy, or program : In situations where it is not feasible or ethical to randomly assign participants to intervention and control groups, quasi-experimental designs can be used to evaluate the impact of the intervention on the targeted outcome.
• When the sample size is small: In situations where the sample size is small, it may be difficult to randomly assign participants to intervention and control groups. Quasi-experimental designs can be used to investigate the impact of an intervention without requiring a large sample size.
• When the research question involves investigating a naturally occurring event : In some situations, researchers may be interested in investigating the impact of a naturally occurring event, such as a natural disaster or a major policy change. Quasi-experimental designs can be used to evaluate the impact of the event on the targeted outcome.
• When the research question involves investigating a long-term intervention: In situations where the intervention or program is long-term, it may be difficult to randomly assign participants to intervention and control groups for the entire duration of the intervention. Quasi-experimental designs can be used to evaluate the impact of the intervention over time.
• When the research question involves investigating the impact of a variable that cannot be manipulated : In some situations, it may not be possible or ethical to manipulate a variable of interest. Quasi-experimental designs can be used to investigate the relationship between the variable and the targeted outcome.

Purpose of Quasi-Experimental Design

The purpose of quasi-experimental design is to investigate the causal relationship between two or more variables when it is not feasible or ethical to conduct a randomized controlled trial (RCT). Quasi-experimental designs attempt to emulate the randomized control trial by mimicking the control group and the intervention group as much as possible.

The key purpose of quasi-experimental design is to evaluate the impact of an intervention, policy, or program on a targeted outcome while controlling for potential confounding factors that may affect the outcome. Quasi-experimental designs aim to answer questions such as: Did the intervention cause the change in the outcome? Would the outcome have changed without the intervention? And was the intervention effective in achieving its intended goals?

Quasi-experimental designs are useful in situations where randomized controlled trials are not feasible or ethical. They provide researchers with an alternative method to evaluate the effectiveness of interventions, policies, and programs in real-life settings. Quasi-experimental designs can also help inform policy and practice by providing valuable insights into the causal relationships between variables.

Overall, the purpose of quasi-experimental design is to provide a rigorous method for evaluating the impact of interventions, policies, and programs while controlling for potential confounding factors that may affect the outcome.

Advantages of Quasi-Experimental Design

Quasi-experimental designs have several advantages over other research designs, such as:

• Greater external validity : Quasi-experimental designs are more likely to have greater external validity than laboratory experiments because they are conducted in naturalistic settings. This means that the results are more likely to generalize to real-world situations.
• Ethical considerations: Quasi-experimental designs often involve naturally occurring events, such as natural disasters or policy changes. This means that researchers do not need to manipulate variables, which can raise ethical concerns.
• More practical: Quasi-experimental designs are often more practical than experimental designs because they are less expensive and easier to conduct. They can also be used to evaluate programs or policies that have already been implemented, which can save time and resources.
• No random assignment: Quasi-experimental designs do not require random assignment, which can be difficult or impossible in some cases, such as when studying the effects of a natural disaster. This means that researchers can still make causal inferences, although they must use statistical techniques to control for potential confounding variables.
• Greater generalizability : Quasi-experimental designs are often more generalizable than experimental designs because they include a wider range of participants and conditions. This can make the results more applicable to different populations and settings.

Limitations of Quasi-Experimental Design

There are several limitations associated with quasi-experimental designs, which include:

• Lack of Randomization: Quasi-experimental designs do not involve randomization of participants into groups, which means that the groups being studied may differ in important ways that could affect the outcome of the study. This can lead to problems with internal validity and limit the ability to make causal inferences.
• Selection Bias: Quasi-experimental designs may suffer from selection bias because participants are not randomly assigned to groups. Participants may self-select into groups or be assigned based on pre-existing characteristics, which may introduce bias into the study.
• History and Maturation: Quasi-experimental designs are susceptible to history and maturation effects, where the passage of time or other events may influence the outcome of the study.
• Lack of Control: Quasi-experimental designs may lack control over extraneous variables that could influence the outcome of the study. This can limit the ability to draw causal inferences from the study.
• Limited Generalizability: Quasi-experimental designs may have limited generalizability because the results may only apply to the specific population and context being studied.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Questionnaire – Definition, Types, and Examples

Ethnographic Research -Types, Methods and Guide

One-to-One Interview – Methods and Guide

Quantitative Research – Methods, Types and...

Explanatory Research – Types, Methods, Guide

Qualitative Research – Methods, Analysis Types...

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Quasi-Experimental Designs for Causal Inference

Yongnam kim, peter steiner.

• Author information
• Article notes
• Copyright and License information

Correspondence should be addressed to Yongnam Kim, Department of Educational Psychology, University of Wisconsin–Madison, 859 Education Sciences, 1025 W Johnson Street, Madison, WI 53706-1796. [email protected]

Issue date 2016.

When randomized experiments are infeasible, quasi-experimental designs can be exploited to evaluate causal treatment effects. The strongest quasi-experimental designs for causal inference are regression discontinuity designs, instrumental variable designs, matching and propensity score designs, and comparative interrupted time series designs. This article introduces for each design the basic rationale, discusses the assumptions required for identifying a causal effect, outlines methods for estimating the effect, and highlights potential validity threats and strategies for dealing with them. Causal estimands and identification results are formalized with the potential outcomes notations of the Rubin causal model.

Causal inference plays a central role in many social and behavioral sciences, including psychology and education. But drawing valid causal conclusions is challenging because they are warranted only if the study design meets a set of strong and frequently untestable assumptions. Thus, studies aiming at causal inference should employ designs and design elements that are able to rule out most plausible threats to validity. Randomized controlled trials (RCTs) are considered as the gold standard for causal inference because they rely on the fewest and weakest assumptions. But under certain conditions quasi-experimental designs that lack random assignment can also be as credible as RCTs ( Shadish, Cook, & Campbell, 2002 ).

This article discusses four of the strongest quasi-experimental designs for identifying causal effects: regression discontinuity design, instrumental variable design, matching and propensity score designs, and the comparative interrupted time series design. For each design we outline the strategy and assumptions for identifying a causal effect, address estimation methods, and discuss practical issues and suggestions for strengthening the basic designs. To highlight the design differences, throughout the article we use a hypothetical example with the following causal research question: What is the effect of attending a summer science camp on students’ science achievement?

POTENTIAL OUTCOMES AND RANDOMIZED CONTROLLED TRIAL

Before we discuss the four quasi-experimental designs, we introduce the potential outcomes notation of the Rubin causal model (RCM) and show how it is used in the context of an RCT. The RCM ( Holland, 1986 ) formalizes causal inference in terms of potential outcomes, which allow us to precisely define causal quantities of interest and to explicate the assumptions required for identifying them. RCM considers a potential outcome for each possible treatment condition. For a dichotomous treatment variable (i.e., a treatment and control condition), each subject i has a potential treatment outcome Y i (1), which we would observe if subject i receives the treatment ( Z i = 1), and a potential control outcome Y i (0), which we would observe if subject i receives the control condition ( Z i = 0). The difference in the two potential outcomes, Y i (1)− Y i (0), represents the individual causal effect.

Suppose we want to evaluate the effect of attending a summer science camp on students’ science achievement score. Then each student has two potential outcomes: a potential control score for not attending the science camp, and the potential treatment score for attending the camp. However, the individual causal effects of attending the camp cannot be inferred from data, because the two potential outcomes are never observed simultaneously. Instead, researchers typically focus on average causal effects. The average treatment effect (ATE) for the entire study population is defined as the difference in the expected potential outcomes, ATE = E [ Y i (1)] − E [ Y i (0)]. Similarly, we can also define the ATE for the treated subjects (ATT), ATT = E [ Y i (1) | Z i = 1] − E [ Y (0) | Z i =1]. Although the expectations of the potential outcomes are not directly observable because not all potential outcomes are observed, we nonetheless can identify ATE or ATT under some reasonable assumptions. In an RCT, random assignment establishes independence between the potential outcomes and the treatment status, which allows us to infer ATE. Suppose that students are randomly assigned to the science camp and that all students comply with the assigned condition. Then random assignment guarantees that the camp attendance indicator Z is independent of the potential achievement scores Y i (0) and Y i (1).

The independence assumption allows us to rewrite ATE in terms of observable expectations (i.e., with observed outcomes instead of potential outcomes). First, due to the independence (randomization), the unconditional expectations of the potential outcomes can be expressed as conditional expectations, E [ Y i (1)] = E [ Y i (1) | Z i = 1] and E [ Y i (0)] = E [ Y i (0) | Z i = 0] Second, because the potential treatment outcomes are actually observed for the treated, we can replace the potential treatment outcome with the observed outcome such that E [ Y i (1) | Z i = 1] = E [ Y i | Z i = 1] and, analogously, E [ Y i (0) | Z i = 0] = E [ Y i | Z i = 0] Thus, the ATE is expressible in terms of observable quantities rather than potential outcomes, ATE = E [ Y i (1)] − E [ Y i (0)] = E [ Y i | Z i = 1] – E [ Y i | Z i = 0], and we that say ATE is identified.

This derivation also rests on the stable-unit-treatment-value assumption (SUTVA; Imbens & Rubin, 2015 ). SUTVA is required to properly define the potential outcomes, that is, (a) the potential outcomes of a subject depend neither on the assignment mode nor on other subjects’ treatment assignment, and (b) there is only one unique treatment and one unique control condition. Without further mentioning, we assume SUTVA for all quasi-experimental designs discussed in this article.

REGRESSION DISCONTINUITY DESIGN

Due to ethical or budgetary reasons, random assignment is often infeasible in practice. Nonetheless, researchers may sometimes still retain full control over treatment assignment as in a regression discontinuity (RD) design where, based on a continuous assignment variable and a cutoff score, subjects are deterministically assigned to treatment conditions.

Suppose that the science camp is a remedial program and only students whose grade point average (GPA) score is less than or equal to 2.0 are eligible to participate. Figure 1 shows a scatterplot of hypothetical data where the x-axis represents the assignment variable ( GPA ) and the y -axis the outcome ( Science Score ). All subjects with a GPA score below the cutoff attended the camp (circles), whereas all subjects scoring above the cutoff do not attend (squares). Because all low-achieving students are in the treatment group and all high-achieving students in the control group, their respective GPA distributions do not overlap, not even at the cutoff. This lack of overlap complicates the identification of a causal effect because students in the treatment and control group are not comparable at all (i.e., they have a completely different distribution of the GPA scores).

A hypothetical example of regression discontinuity design. Note . GPA = grade point average.

One strategy of dealing with the lack of overlap is to rely on the linearity assumption of regression models and to extrapolate into areas of nonoverlap. However, if the linear models do not correctly specify the functional form, the resulting ATE estimate is biased. A safer strategy is to evaluate the treatment effect only at the cutoff score where treatment and control cases almost overlap, and thus functional form assumptions and extrapolation are almost no longer needed. Consider the treatment and control students that score right at the cutoff or just above it. Students with a GPA score of 2.0 participate in the science camp and students with a GPA score of 2.1 are in the control condition (the status quo condition or a different camp). The two groups of students are essentially equivalent because the difference in their GPA scores is negligibly small (2.1 − 2.0 = .1) and likely due to random chance (measurement error) rather than a real difference in ability. Thus, in the very close neighborhood around the cutoff score, the RD design is equivalent to an RCT; therefore, the ATE at the cutoff (ATEC) is identified.

CAUSAL ESTIMAND AND IDENTIFICATION

ATEC is defined as the difference in the expected potential treatment and control outcomes for the subjects scoring exactly at the cutoff: ATEC = E [ Y i (1) | A i = a c ] − E [ Y i (0) | A i = a c ], where A denotes assignment variable and a c the cutoff score. Because we observe only treatment subjects and not control subjects right at the cutoff, we need two assumptions in order to identify ATEC ( Hahn, Todd, & van Klaauw, 2001 ): (a) the conditional expectations of the potential treatment and control outcomes are continuous at the cutoff ( continuity ), and (b) all subjects comply with treatment assignment ( full compliance ).

The continuity assumption can be expressed in terms of limits as lim a ↓ a C E [ Y i ( 1 ) | A i = a ] = E [ Y i ( 1 ) | A i = a ] = lim a ↑ a C E [ Y i ( 1 ) | A i = a ] and lim a ↓ a C E [ Y i ( 0 ) | A i = a ] = E [ Y i ( 0 ) | A i = a ] = lim a ↑ a C E [ Y i ( 0 ) | A i = a ] . Thus, we can rewrite ATEC as the difference in limits, A T E C = lim a ↑ a C E [ Y i ( 1 ) | A i = a c ] − lim a ↓ a C E [ Y i ( 0 ) | A i = a c ] , which solves the issue that no control subjects are observed directly at the cutoff. Then, by the full compliance assumption, the potential treatment and control outcomes can be replaced with the observed outcomes such that A T E C = lim a ↑ a C E [ Y i | A i = a c ] − lim a ↓ a C E [ Y i | A i = a c ] is identified at the cutoff (i.e., ATEC is now expressed in terms of observable quantities). The difference in the limits represents the discontinuity in the mean outcomes exactly at the cutoff ( Figure 1 ).

Estimating ATEC

ATEC can be estimated with parametric or nonparametric regression methods. First, consider the parametric regression of the outcome Y on the treatment Z , the cutoff-centered assignment variable A − a c , and their interaction: Y = β 0 + β 1 Z + β 2 ( A − a c ) + β 3 ( Z × ( A − a c )) + e . If the model correctly specifies the functional form, then β ^ 1 is an unbiased estimator for ATEC. In practice, an appropriate model specification frequently involves also quadratic and cubic terms of the assignment variable plus their interactions with the treatment indicator.

To avoid overly strong functional form assumptions, semiparametric or nonparametric regression methods like generalized additive models or local linear kernel regression can be employed ( Imbens & Lemieux, 2008 ). These methods down-weight or even discard observations that are not in the close neighborhood around the cutoff. The R packages rdd ( Dimmery, 2013 ) and rdrobust ( Calonico, Cattaneo, & Titiunik, 2015 ), or the command rd in STATA ( Nichols, 2007 ) are useful for estimation and diagnostic purposes.

Practical Issues

A major validity threat for RD designs is the manipulation of the assignment score around the cutoff, which directly results in a violation of the continuity assumption ( Wong et al., 2012 ). For instance, if a teacher knows the assignment score in advance and he wants all his students to attend the science camp, the teacher could falsely report a GPA score of 2.0 or below for the students whose actual GPA score exceeds the cutoff value.

Another validity threat is noncompliance, meaning that subjects assigned to the control condition may cross over to the treatment and subjects assigned to the treatment do not show up. An RD design with noncompliance is called a fuzzy RD design (instead of a sharp RD design with full compliance). A fuzzy RD design still allows us to identify the intention-to-treat effect or the local average treatment effect at the cutoff (LATEC). The intention-to-treat effect refers to the effect of treatment assignment rather than the actual treatment receipt. LATEC estimates ATEC for the subjects who comply with treatment assignment. LATEC is identified if one uses the assignment status as an instrumental variable for treatment receipt (see the upcoming Instrumental Variable section).

Finally, generalizability and statistical power are often mentioned as major disadvantages of RD designs. Because RD designs identify the treatment effect only at the cutoff, ATEC estimates are not automatically generalizable to subjects scoring further away from the cutoff. Statistical power for detecting a significant effect is an issue because the lack of overlap on the assignment variable results in increased standard errors. With semi- or nonparametric regression methods, power further diminishes.

Strengthening RD Designs

To avoid systematic manipulations of the assignment variable, it is desirable to conceal the assignment rule from study participants and administrators. If the assignment rule is known to them, manipulations can hardly be ruled out, particularly when the stakes are high. Researchers can use the McCrary test ( McCrary, 2008 ) to check for potential manipulations. The test investigates whether there is a discontinuity in the distribution of the assignment variable right at the cutoff. Plotting baseline covariates against the assignment variable, and regressing the covariates on the assignment variable and the treatment indicator also help in detecting potential discontinuities at the cutoff.

The RD design’s validity can be increased by combining the basic RD design with other designs. An example is the tie-breaking RD design, which uses two cutoff scores. Subjects scoring between the two cutoff scores are randomly assigned to treatment conditions, whereas subjects scoring outside the cutoff interval receive the treatment or control condition according to the RD assignment rule ( Black, Galdo & Smith, 2007 ). This design combines an RD design with an RCT and is advantageous with respect to the correct specification of the functional form, generalizability, and statistical power. Similar benefits can be obtained by adding pretest measures of the outcome or nonequivalent comparison groups ( Wing & Cook, 2013 ).

Imbens and Lemieux (2008) and Lee and Lemieux (2010) provided comprehensive introductions to RD designs. Lee and Lemieux also summarized many applications from economics. Angrist and Lavy (1999) applied the design to investigate the effect of class size on student achievement.

INSTRUMENTAL VARIABLE DESIGN

In practice, researchers often have no or only partial control over treatment selection. In addition, they might also lack reliable knowledge of the selection process. Nonetheless, even with limited control and knowledge of the selection process it is still possible to identify a causal treatment effect if an instrumental variable (IV) is available. An IV is an exogenous variable that is related to the treatment but is completely unrelated to the outcome, except via treatment. An IV design requires researchers either to create an IV at the design stage (as in an encouragement design; see next) or to find an IV in the data set at hand or a related data base.

Consider the science camp example, but instead of random or deterministic treatment assignment, students decide on their own or together with their parents whether to attend the camp. Many factors may determine the decision, for instance, students’ science ability and motivation, parents’ socioeconomic status, or the availability of public transportation for the daily commute to the camp. Whereas the first three variables are presumably also related to the science outcome, public transportation might be unrelated to the science score (except via camp attendance). Thus, the availability of public transportation may qualify as an IV. Figure 2 illustrates such IV design: Public transportation (IV) directly affects camp attendance but has no direct or indirect effect on science achievement (outcome) other than through camp attendance (treatment). The question mark represents unknown or unobserved confounders, that is, variables that simultaneously affect both camp attendance and science achievement. The IV design allows us to identify a causal effect even if some or all confounders are unknown or unobserved.

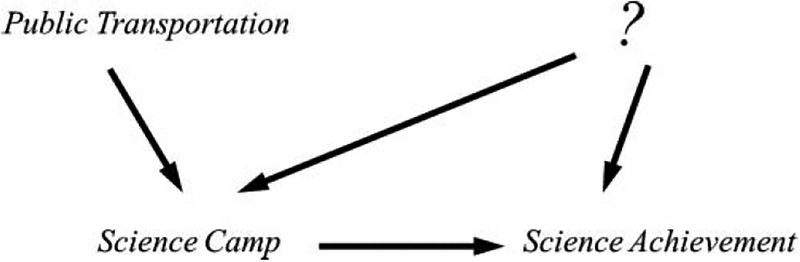
A diagram of an example of instrumental variable design.

The strategy for identifying a causal effect is based on exploiting the variation in the treatment variable explained by IV. In Figure 2 , the total variation in the treatment consists of (a) the variation induced by the IV and (b) the variation induced by confounders (question mark) and other exogenous variables (not shown in the figure). The identification of the camp’s effect requires us to isolate the treatment variation that is related to public transportation (IV), and then to use the isolated variation to investigate the camp’s effect on the science score. Because we exploit the treatment variation exclusively induced by the IV but ignore the variation induced by unobserved or unknown confounders, the IV design identifies the ATE for the sub-population of compliers only. In our example, the compliers are the students who attend the camp because public transportation is available and do not attend because it is unavailable. For students whose parents always use their own car to drop them off and pick them up at the camp location, we cannot infer the causal effect, because their camp attendance is completely unrelated to the availability of public transportation.

Causal Estimand and Identification

The complier average treatment effect (CATE) is defined as the expected difference in potential outcomes for the sub-population of compliers: CATE = E [ Y i (1) | Complier ] − E [ Y i (0) | Complier ] = τ C .

Identification requires us to distinguish between four latent groups: compliers (C), who attend the camp if public transportation is available but do not attend if unavailable; always-takers (A), who always attend the camp regardless of whether or not public transportation is available; never-takers (N), who never attend the camp regardless of public transportation; and defiers (D), who do not attend if public transportation is available but attend if unavailable. Because group membership is unknown, it is impossible to directly infer CATE from the data of compliers. However, CATE is identified from the entire data set if (a) the IV is predictive of the treatment ( predictive first stage ), (b) the IV is unrelated to the outcome except via treatment ( exclusion restriction ), and (c) no defiers are present ( monotonicity ; Angrist, Imbens, & Rubin, 1996 ; see Steiner, Kim, Hall, & Su, 2015 , for a graphical explanation).

First, notice that the IV’s effects on the treatment (γ) and the outcome (δ) are directly identified from the observed data because the IV’s relation with the treatment and outcome is unconfounded. In our example ( Figure 2 ), γ denotes the effect of public transportation on camp attendance and δ the indirect effect of public transportation on the science score. Both effects can be written as weighted averages of the corresponding group-specific effects ( γ C , γ A , γ N , γ D and δ C , δ A , δ N , δ D for compliers, always-takers, never-takers, and defiers, respectively): γ = p ( C ) γ C + p ( A ) γA + p ( N ) γ N + p ( D ) γ D and δ = p ( C ) δ C + p ( A ) δ A + p ( N ) δ N + p ( D ) δ D where p (.) represents the portion of the respective latent group in the population and p ( C ) + p ( A ) + p ( N ) + p ( D ) = 1. Because the treatment choice of always-takers and never-takers is entirely unaffected by the instrument, the IV’s effect on the treatment is zero, γ A = γ N = .0, and together with the exclusion restriction , we also know δ A = δ N = 0, that is, the IV has no effect on the outcome. If no defiers are present, p ( D ) = 0 ( monotonicity ), then the IV’s effects on the treatment and outcome simplify to γ = p ( C ) γC and δ = p ( C ) δC , respectively. Because δ C = γ C τ C and γ ≠ 0 ( predictive first stage ), the ratio of the observable IV effects, γ and δ, identifies CATE: δ γ = p ( C ) γ C τ C p ( C ) γ C = τ C .

Estimating CATE

A two-stage least squares (2SLS) regression is typically used for estimating CATE. In the first stage, treatment Z is regressed on the IV, Z = β 0 + β 1 IV + e . The linear first-stage model applies with a dichotomous treatment variable (linear probability model). The second stage then regresses the outcome Y on the predicted values Z ^ from the first stage model, Y = π 0 + π 1 Z ^ + r , where π ^ 1 is the CATE estimator. The two stages are automatically performed by the 2SLS procedure, which also provides an appropriate standard error for the effect estimate. The STATA commands ivregress and ivreg2 ( Baum, Schaffer, & Stillman, 2007 ) or the sem package in R ( Fox, 2006 ) perform the 2SLS regression.

One challenge in implementing an IV design is to find a valid instrument that satisfies the assumptions just discussed. In particular, the exclusion restriction is untestable and frequently hard to defend in practice. In our example, if high-income families live in suburban areas with bad public transportation connections, then the availability of the public transportation is likely related to the science score via household income (or socioeconomic status). Although conditioning on the observed household income can transform public transportation into a conditional IV (see next), one can frequently come up with additional scenarios that explains why the IV is related to the outcome and thus violates the exclusion restriction.

Another issue arises from “weak” IVs that are only weakly related to treatment. Weak IVs cause efficiency problems ( Wooldridge, 2012 ). If the availability of public transportation barely affects camp attendance because most parents give their children a ride anyway, the IV’s effect on the treatment ( γ ) is close to zero. Because γ ^ is the denominator in the CATE estimator, τ ^ C = δ ^ / γ ^ , an imprecisely estimated γ ^ results in a considerable over- or underestimation of CATE. Moreover, standard errors will be large.

One also needs to keep in mind that the substantive meaning of CATE depends on the chosen IV. Consider two slightly different IVs with respect to public transportation: the availability of (a) a bus service and (b) subway service. For the first IV, the complier population consists of students who choose to (not) attend the camp depending on the availability of a bus service. For the second IV, the complier population refers to the availability of a subway service. Because the two complier populations are very likely different from each other (students who are willing to take the subway might not be willing to take the bus), the corresponding CATEs refer to different subpopulations.

Strengthening IV Designs

Given the challenges in identifying a valid instrument from observed data, researchers should consider creating an IV at the design stage of a study. Although it might be impossible to directly assign subjects to treatment conditions, one might still be able to encourage participants to take the treatment. Subjects are randomly encouraged to sign up for treatment, but whether they actually comply with the encouragement is entirely their own decision ( Imai et al., 2011 ). Random encouragement qualifies as an IV because it very likely meets the exclusion restriction. For example, instead of collecting data on public transportation, researchers may advertise and recommend the science camp in a letter to the parents of a randomly selected sample of students.

With observational data it is hard to identify a valid IV because covariates that strongly predict the treatment are usually also related to the outcome. However, these covariates can still qualify as an IV if they affect the outcome only indirectly via other observed variables. Such covariates can be used as conditional IVs, that is, they meet the IV requirements conditional on the observed variables ( Brito & Pearl, 2002 ). Assume the availability of public transportation (IV) is associated with the science score via household income. Then, controlling for the reliably measured household income in both stages of the 2SLS analysis blocks the IV’s relation to the science score and turns public transportation into a conditional IV. However, controlling for a large set of variables does not guarantee that the exclusion restriction is more likely met. It may even result in more bias as compared to an IV analysis with fewer covariates ( Ding & Miratrix, 2015 ; Steiner & Kim, in press ). The choice of a valid conditional IV requires researchers to carefully select the control variables based on subject-matter theory.

The seminal article by Angrist et al. (1996) provides a thorough discussion of the IV design, and Steiner, Kim, et al. (2015 ) proved the identification result using graphical models. Excellent introductions to IV designs can be found in Angrist and Pischke (2009 , 2015) . Angrist and Krueger (1992) is an example of a creative application of the design with birthday as the IV. For encouragement designs, see Holland (1988) and Imai et al. (2011) .

MATCHING AND PROPENSITY SCORE DESIGN

This section considers quasi-experimental designs in which researchers lack control over treatment selection but have good knowledge about the selection mechanism or at least the confounders that simultaneously determine the treatment selection and the outcome. Due to self or third-person selection of subjects into treatment, the resulting treatment and control groups typically differ in observed but also unobserved baseline covariates. If we have reliable measures of all confounding covariates, then matching or propensity score (PS) designs balance groups on observed baseline covariates and thus enable the identification of causal effects ( Imbens & Rubin, 2015 ). Regression analysis and the analysis of covariance can also remove the confounding bias, but because they rely on functional form assumptions and extrapolation we discuss only nonparametric matching and PS designs.

Suppose that students decide on their own whether to attend the science camp. Although many factors can affect students’ decision, teachers with several years of experience of running the camp may know that selection is mostly driven by students’ science ability, liking of science, and their parents’ socioeconomic status. If all the selection-relevant factors that also affect the outcome are known, the question mark in Figure 2 can be replaced by the known confounding covariates.

Given the set of confounding covariates, causal inference with matching or PS designs is straightforward, at least theoretically. The basic one-to-one matching design matches each treatment subject to a control subject that is equivalent or at least very similar in observed covariates. To illustrate the idea of matching, consider a camp attendee with baseline measures of 80 on the science pre-test, 6 on liking science, and 50 on the socioeconomic status. Then a multivariate matching strategy tries to find a nonattendee with exactly the same or at least very similar baseline measures. If we succeed in finding close matches for all camp attendee, the matched samples of attendees and nonattendees will have almost identical covariate distributions.

Although multivariate matching works well when the number of confounders is small and the pool of control subjects is large relative to the number of treatment subjects, it is usually difficult to find close matches with a large set of covariates or a small pool of control subjects. Matching on the PS helps to overcome this issue because the PS is a univariate score computed from the observed covariates ( Rosenbaum & Rubin, 1983 ). The PS is formally defined as the conditional probability of receiving the treatment given the set of observed covariates X : PS = Pr( Z = 1 | X ).

Matching and PS designs usually investigate ATE = E [ Y i (1)] − E [ Y i (0)] or ATT = E [ Y i (1) | Z i = 1] – E [ Y i (0) | Z i = 1]. Both causal effects are identified if (a) the potential outcomes are statistically independent of the treatment indicator given the set of observed confounders X , { Y (1), Y (0)}⊥ Z | X ( unconfoundedness ; ⊥ denotes independence), and (b) the treatment probability is strictly between zero and one, 0 < Pr( Z = 1 | X ) < 1 ( positivity ).

By the positivity assumption we get E [ Y i (1)] = E X [ E [ Y i (1) | X ]] and E [ Y i (0)] = E X [ E [ Y i (0) | X ]]. If the unconfoundedness assumption holds, we can write the inner expectations as E [ Y i (1) | X ] = E [ Y i (1) | Z i =1; X ] and E [ Y i (0) | X ] = E [ Y i (0) | Z i = 0; X ]. Finally, because the treatment (control) outcomes of the treatment (control) subjects are actually observed, ATE is identified because it can be expressed in terms of observable quantities: ATE = E X [ E [ Y i | Z i = 1; X ]] – E X [ E [ Y i | Z i = 0; X ]]. The same can be shown for ATT. The unconfoundedness and positivity assumption are frequently referred to jointly as the strong ignorability assumption. Rosenbaum and Rubin (1983) proved that if the assignment is strongly ignorable given X , then it is also strongly ignorable given the PS alone.

Estimating ATE and ATT

Matching designs use a distance measure for matching each treatment subject to the closest control subject. The Mahalanobis distance is usually used for multivariate matching and the Euclidean distance on the logit of the PS for PS matching. Matching strategies differ with respect to the matching ratio (one-to-one or one-to-many), replacement of matched subjects (with or without replacement), use of a caliper (treatment subjects that do not have a control subject within a certain threshold remain unmatched), and the matching algorithm (greedy, genetic, or optimal matching; Sekhon, 2011 ; Steiner & Cook, 2013 ). Because we try to find at least one control subject for each treatment subject, matching estimators typically estimate ATT. Once treatment and control subjects are matched, ATT is computed as the difference in the mean outcome of the treatment and control group. An alternative matching strategy that allows for estimating ATE is full matching, which stratifies all subjects into the maximum number of strata, where each stratum contains at least one treatment and one control subject ( Hansen, 2004 ).

The PS can also be used for PS stratification and inverse-propensity weighting. PS stratification stratifies the treatment and control subjects into at least five strata and estimates the treatment effect within each stratum. ATE or ATT is then obtained as the weighted average of the stratum-specific treatment effects. Inverse-propensity weighting follows the same logic as inverse-probability weighting in survey research ( Horvitz & Thompson, 1952 ) and requires the computation of weights that refer to either the overall population (ATE) or the population of treated subjects only (ATT). Given the inverse-propensity weights, ATE or ATT is usually estimated via weighted least squares regression.

Because the true PSs are unknown, they need to be estimated from the observed data. The most common method for estimating the PS is logistic regression, which regresses the binary treatment indicator Z on predictors of the observed covariates. The PS model is specified according to balance criteria (instead of goodness of fit criteria), that is, the estimated PSs should remove all baseline differences in observed covariates ( Imbens & Rubin, 2015 ). The predicted probabilities from the PS model represent the estimated PSs.

All three PS designs—matching, stratification, and weighting—can benefit from additional covariance adjustments in an outcome regression. That is, for the matched, stratified or weighted data, the outcome is regressed on the treatment indicator and the additional covariates. Combining the PS design with a covariance adjustment gives researchers two chances to remove the confounding bias, by correctly specifying either the PS model or the outcome model. These combined methods are said to be doubly robust because they are robust against either the misspecification of the PS model or the misspecification of the outcome model ( Robins & Rotnitzky, 1995 ). The R packages optmatch ( Hansen & Klopfer, 2006 ) and MatchIt ( Ho et al., 2011 ) and the STATA command teffects , in particular teffects psmatch ( StataCorp, 2015 ), can be useful for matching or PS analyses.

The most challenging issue with matching and PS designs is the selection of covariates for establishing unconfoundedness. Ideally, subject-matter theory about the selection process and the outcome-generating model is used for selecting a set of covariates that removes all the confounding ( Pearl, 2009 ). If strong subject-matter theories are not available, selecting the right covariates is difficult. In the hope to remove a major part of the confounding bias—if not all of it—a frequently applied strategy is to match on as many covariates as possible. However, recent literature shows that thoughtless inclusion of covariates may increase rather than reduce the confounding bias ( Pearl, 2010 ; Steiner & Kim, in press). The risk of increasing bias can be reduced if the observed covariates cover a broad range of heterogeneous construct domains, including at least one reliable pretest measure of the outcome ( Steiner, Cook, et al., 2015 ). Besides having the right covariates, they also need to be reliably measured. The unreliable measurement of confounding covariates has a similar effect as the omission of a confounder: It results in a violation of the unconfoundedness assumption and thus in a biased effect estimate ( Steiner, Cook, & Shadish, 2011 ; Steiner & Kim, in press ).

Even if the set of reliably measured covariates establishes unconfoundedness, we still need to correctly specify the functional form of the PS model. Although parametric models like logistic regression, including higher order terms, might frequently approximate the correct functional form, they still rely on the linearity assumption. The linearity assumption can be relaxed if one estimates the PS with statistical learning algorithms like classification trees, neural networks, or the LASSO ( Keller, Kim, & Steiner, 2015 ; McCaffrey, Ridgeway, & Morral, 2004 ).

Strengthening Matching and PS Designs

The credibility of matching and PS designs heavily relies on the unconfoundedness assumption. Although empirically untestable, there are indirect ways for assessing unconfoundedness. First, unaffected (nonequivalent) outcomes that are known to be unaffected by the treatment can be used ( Shadish et al., 2002 ). For instance, we may expect that attendance in the science camp does not significantly affect the reading score. Thus, if we observe a significant group difference in the reading score after the PS adjustment, bias due to unobserved confounders (e.g., general intelligence) is still likely. Second, adding a second but conceptually different control group allows for a similar test as with the unaffected outcome ( Rosenbaum, 2002 ).

Because researchers rarely know whether the unconfoundedness assumption is actually met with the data at hand, it is important to assess the effect estimate’s sensitivity to potentially unobserved confounders. Sensitivity analyses investigate how strongly an estimate’s magnitude and significance changes if a confounder of a certain strength would have been omitted from the analyses. Causal conclusions are much more credible if the effect’s direction, magnitude, and significance is rather insensitive to omitted confounders ( Rosenbaum, 2002 ). However, despite the value of sensitivity analyses, they are not informative about whether hidden bias is actually present.

Schafer and Kang (2008) and Steiner and Cook (2013) provided a comprehensive introduction. Rigorous formalization and technical details of PS designs can be found in Imbens and Rubin (2015) . Rosenbaum (2002) discussed many important design issues in these designs.

COMPARATIVE INTERRUPTED TIME SERIES DESIGN

The designs discussed so far require researchers to have either full control over treatment assignment or reliable knowledge of the exogenous (IV) or endogenous part of the selection mechanism (i.e., the confounders). If none of these requirements are met, a comparative interrupted time series (CITS) design might be a viable alternative if (a) multiple measurements of the outcome ( time series ) are available for both the treatment and a comparison group and (b) the treatment group’s time series has been interrupted by an intervention.

Suppose that all students of one class in a school (say, an advanced science class) attend the camp, whereas all students of another class in the same school do not attend. Also assume that monthly measures of science achievement before and after the science camp are available. Figure 3 illustrates such a scenario where the x -axis represents time in Months and the y -axis the Science Score (aggregated at the class level). The filled symbols indicate the treatment group (science camp), open symbols the comparison group (no science camp). The science camp intervention divides both time series into a preintervention time series (circles) and a postintervention time series (squares). The changes in the levels and slopes of the pre- and postintervention regression lines represent the camp’s impact but possibly also the effect of other events that co-occur with the intervention. The dashed lines extrapolate the preintervention growth curves into the postintervention period, and thus represent the counterfactual situation where the intervention but also other co-occurring events are absent.

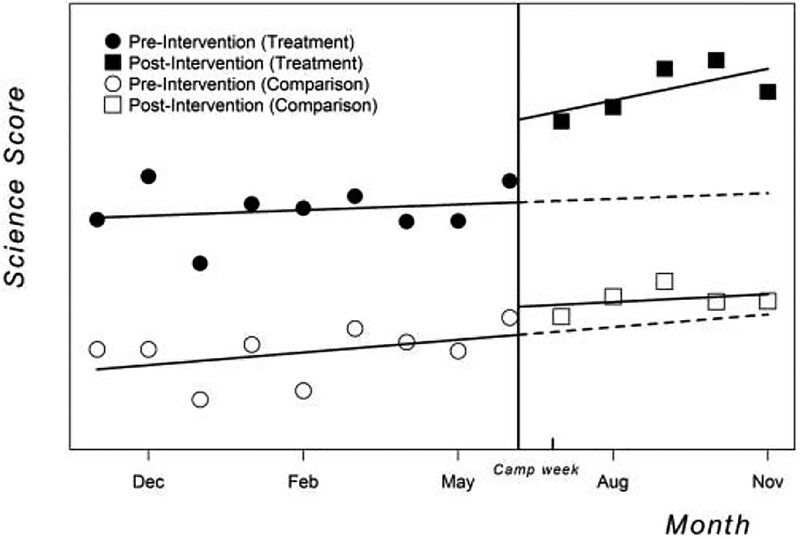
A hypothetical example of comparative interrupted time series design.

The strength of a CITS design is its ability to discriminate between the intervention’s effect and the effects of co-occurring events. Such events might be other potentially competing interventions (history effects) or changes in the measurement of the outcome (instrumentation), for instance. If the co-occurring events affect the treatment and comparison group to the same extent, then subtracting the changes in the comparison group’s growth curve from the changes in the treatment group’s growth curve provides a valid estimate of the intervention’s impact. Because we investigate the difference in the changes (= differences) of the two growth curves, the CITS design is a special case of the difference-in-differences design ( Somers et al., 2013 ).

Assume that a daily TV series about Albert Einstein was broadcast in the evenings of the science camp week and that students of both classes were exposed to the same extent to the TV series. It follows that the comparison group’s change in the growth curve represents the TV series’ impact. The comparison group’s time series in Figure 3 indicates that the TV series might have had an immediate impact on the growth curve’s level but almost no effect on the slope. On the other hand, the treatment group’s change in the growth curve is due to both the science camp and the TV series. Thus, in differencing out the TV series’ effect (estimated from the comparison group) we can identify the camp effect.

Let t c denote the time point of the intervention, then the intervention’s effect on the treated (ATT) at a postintervention time point t ≥ t c is defined as τ t = E [ Y i t T ( 1 ) ] − E [ Y i t T ( 0 ) ] , where Y i t T ( 0 ) and Y i t T ( 1 ) are the potential control and treatment outcomes of subject i in the treatment group ( T ) at time point t . The time series of the expected potential outcomes can be formalized as sum of nonparametric but additive time-dependent functions. The treatment group’s expected potential control outcome can be represented as E [ Y i t T ( 0 ) ] = f 0 T ( t ) + f E T ( t ) , where the control function f 0 T ( t ) generates the expected potential control outcomes in absence of any interventions ( I ) or co-occurring events ( E ), and the event function f E T ( t ) adds the effects of co-occurring events. Similarly, the expected potential treatment outcome can be written as E [ Y i t T ( 1 ) ] = f 0 T ( t ) + f E T ( t ) + f I T ( t ) , which adds the intervention’s effect τ t = f I T ( t ) to the control and event function. In the absence of a comparison group, we can try to identify the impact of the intervention by comparing the observable postintervention outcomes to the extrapolated outcomes from the preintervention time series (dashed line in Figure 3 ). Extrapolation is necessary because we do not observe any potential control outcomes in the postintervention period (only potential treatment outcomes are observed). Let f ^ 0 T ( t ) denote the parametric extrapolation of the preintervention control function f 0 T ( t ) , then the observable pre–post-intervention difference ( PP T ) in the expected control outcome is P P t T = f 0 T ( t ) + f E T ( t ) + f I T ( t ) − f ^ 0 T ( t ) = f I T ( t ) + ( f 0 T ( t ) − f ^ 0 T ( t ) ) + f E T ( t ) . Thus, in the absence of a comparison group, ATT is identified (i.e., P P t T = f I T ( t ) = τ t ) only if the control function is correctly specified ( f 0 T ( t ) = f ^ 0 T ( t ) ) and if no co-occurring events are present ( f E T ( t ) = 0 ).

The comparison group in a CITS design allows us to relax both of these identifying assumptions. In order to see this, we first define the expected control outcomes of the comparison group ( C ) as a sum of two time-dependent functions as before: E [ Y i t C ( 0 ) ] = f 0 C ( t ) + f E C ( t ) . Then, in extrapolating the comparison group’s preintervention function into the postintervention period, f ^ 0 C ( t ) , we can compute the pre–post-intervention difference for the comparison group: P P t C = f 0 C ( t ) + f E C ( t ) − f ^ 0 C ( t ) = f E C ( t ) + ( f 0 C ( t ) − f ^ 0 C ( t ) ) If the control function is correctly specified f 0 C ( t ) = f ^ 0 C ( t ) , the effect of co-occurring events is identified P P t C = f E C ( t ) . However, we do not necessarily need a correctly specified control function, because in a CITS design we focus on the difference in the treatment and comparison group’s pre–post-intervention differences, that is, P P t T − P P t C = f I T ( t ) + { ( f 0 T ( t ) − f ^ 0 T ( t ) ) − ( f 0 C ( t ) − f ^ 0 C ( t ) ) } + { f E T ( t ) − f E C ( t ) } . Thus, ATT is identified, P P t T − P P t C = f I T ( t ) = τ t , if (a) both control functions are either correctly specified or misspecified to the same additive extent such that ( f 0 T ( t ) − f ^ 0 T ( t ) ) = ( f 0 C ( t ) − f ^ 0 C ( t ) ) ( no differential misspecification ) and (b) the effect of co-occurring events is identical in the treatment and comparison group, f E T ( t ) = f E C ( t ) ( no differential event effects ).

Estimating ATT

CITS designs are typically analyzed with linear regression models that regress the outcome Y on the centered time variable ( T – t c ), the intervention indicator Z ( Z = 0 if t < t c , otherwise Z = 1), the group indicator G ( G = 1 for the treatment group and G = 0 for the control group), and the corresponding two-way and three-way interactions:

Depending on the number of subjects in each group, fixed or random effects for the subjects are included as well (time fixed or random effect can also be considered). β ^ 5 estimates the intervention’s immediate effect at the onset of the intervention (change in intercept) and β ^ 7 the intervention’s effect on the growth rate (change in slope). The inclusion of dummy variables for each postintervention time point (plus their interaction with the intervention and group indicators) would allow for a direct estimation of the time-specific effects. If the time series are long enough (at least 100 time points), then a more careful modeling of the autocorrelation structure via time series models should be considered.

Compared to other designs, CITS designs heavily rely on extrapolation and thus on functional form assumptions. Therefore, it is crucial that the functional forms of the pre- and postintervention time series (including their extrapolations) are correctly specified or at least not differentially misspecified. With short time series or measurement points that inadequately capture periodical variations, the correct specification of the functional form is very challenging. Another specification aspect concerns serial dependencies among the data points. Failing to model serial dependencies can bias effect estimates and their standard errors such that significance tests might be misleading. Accounting for serial dependencies requires autoregressive models (e.g., ARIMA models), but the time series should have at least 100 time points ( West, Biesanz, & Pitts, 2000 ). Standard fixed effects or random effects models deal at least partially with the dependence structure. Robust standard errors (e.g., Huber-White corrected ones) or the bootstrap can also be used to account for dependency structures.

Events that co-occur with the intervention of interest, like history or instrumentation effects, are a major threat to the time series designs that lack a comparison group ( Shadish et al., 2002 ). CITS designs are rather robust to co-occurring events as long as the treatment and comparison groups are affected to the same additive extent. However, there is no guarantee that both groups are exposed to the same events and affected to the same extent. For example, if students who do not attend the camp are less likely to watch the TV series, its effect cannot be completely differenced out (unless the exposure to the TV series is measured). If one uses aggregated data like class or school averages of achievement scores, then differential compositional shifts over time can also invalidate the CITS design. Compositional shifts occur due to dropouts or incoming subjects over time.

Strengthening CITS Designs

If the treatment and comparison group’s preintervention time series are very different (different levels and slopes), then the assumption that history or instrumentation threats affect both groups to the same additive extent may not hold. Matching treatment and comparison subjects prior to the analysis can increase the plausibility of this assumption. Instead of using all nonparticipating students of the comparison class, we may select only those students who have a similar level and growth in the preintervention science scores as the students participating in the camp. We can also match on additional covariates like socioeconomic status or motivation levels. Multivariate or PS matching can be used for this purpose. If the two groups are similar, it is more likely that they are affected by co-occurring events to the same extent.

As with the matching and PS designs, using an unaffected outcome in CITS designs helps to probe the untestable assumptions ( Coryn & Hobson, 2011 ; Shadish et al., 2002 ). For instance, we might expect that attending the science camp does not affect students’ reading scores but that some validity threats (e.g., attrition) operate on both the reading and science outcome. If we find a significant camp effect on the reading score, the validity of the CITS design for evaluating the camp’s impact on the science score is in doubt.

Another strategy to avoid validity threats is to control the time point of the intervention if possible. Researchers can wait with the implementation of the treatment until they have enough preintervention measures for reliably estimating the functional form. They can also choose to intervene when threats to validity are less likely (avoiding the week of the TV series). Control over the intervention also allows researchers to introduce and remove the treatment in subsequent time intervals, maybe even with switching replications between two (or more) groups. If the treatment is effective, we expect that the pattern of the intervention scheme is directly reflected in the time series of the outcome (for more details, see Shadish et al., 2002 ; for the literature on single case designs, see Kazdin, 2011 ).

A comprehensive introduction to CITS design can be found in Shadish et al. (2002) , which also addresses many classical applications. For more technical details of its identification, refer to Lechner (2011) . Wong, Cook, and Steiner (2009) evaluated the effect of No Child Left Behind using a CITS design.

CONCLUDING REMARKS

This article discussed four of the strongest quasi-experimental designs for causal inference when randomized experiments are not feasible. For each design we highlighted the identification strategies and the required assumptions. In practice, it is crucial that the design assumptions are met, otherwise biased effect estimates result. Because most important assumptions like the exclusion restriction or the unconfoundedness assumption are not directly testable, researchers should always try to assess their plausibility via indirect tests and investigate the effect estimates’ sensitivity to violations of these assumptions.

Our discussion of RD, IV, PS, and CITS designs made it also very clear that, in comparison to RCTs, quasi-experimental designs rely on more or stronger assumptions. With prefect control over treatment assignment and treatment implementation (as in an RCT), causal inference is warranted by a minimal set of assumptions. But with limited control over and knowledge about treatment assignment and implementation, stronger assumptions are required and causal effects might be identifiable only for local subpopulations. Nonetheless, observational data sometimes meet the assumptions of a quasi-experimental design, at least approximately, such that causal conclusions are credible. If so, the estimates of quasi-experimental designs—which exploit naturally occurring selection processes and real-world implementations of the treatment—are frequently better generalizable than the results from a controlled laboratory experiment. Thus, if external validity is a major concern, the results of randomized experiments should always be complemented by findings from valid quasi-experiments.

• Angrist JD, Imbens GW, & Rubin DB (1996). Identification of causal effects using instrumental variables. Journal of the American Statistical Association, 91, 444–455. [ Google Scholar ]
• Angrist JD, & Krueger AB (1992). The effect of age at school entry on educational attainment: An application of instrumental variables with moments from two samples. Journal of the American Statistical Association, 87, 328–336. [ Google Scholar ]
• Angrist JD, & Lavy V (1999). Using Maimonides’ rule to estimate the effect of class size on scholastic achievment. Quarterly Journal of Economics, 114, 533–575. [ Google Scholar ]
• Angrist JD, & Pischke JS (2009). Mostly harmless econometrics: An empiricist’s companion. Princeton, NJ: Princeton University Press. [ Google Scholar ]
• Angrist JD, & Pischke JS (2015). Mastering’metrics: The path from cause to effect. Princeton, NJ: Princeton University Press. [ Google Scholar ]
• Baum CF, Schaffer ME, & Stillman S (2007). Enhanced routines for instrumental variables/generalized method of moments estimation and testing. The Stata Journal, 7, 465–506. [ Google Scholar ]
• Black D, Galdo J, & Smith JA (2007). Evaluating the bias of the regression discontinuity design using experimental data (Working paper). Chicago, IL: University of Chicago. [ Google Scholar ]
• Brito C, & Pearl J (2002). Generalized instrumental variables In Darwiche A & Friedman N (Eds.), Uncertainty in artificial intelligence (pp. 85–93). San Francisco, CA: Morgan Kaufmann. [ Google Scholar ]
• Calonico S, Cattaneo MD, & Titiunik R (2015). rdrobust: Robust data-driven statistical inference in regression-discontinuity designs (R package ver. 0.80). Retrieved from http://CRAN.R-project.org/package=rdrobust
• Coryn CLS, & Hobson KA (2011). Using nonequivalent dependent variables to reduce internal validity threats in quasi-experiments: Rationale, history, and examples from practice. New Directions for Evaluation, 131, 31–39. [ Google Scholar ]
• Dimmery D (2013). rdd: Regression discontinuity estimation (R package ver. 0.56). Retrieved from http://CRAN.R-project.org/package=rdd
• Ding P, & Miratrix LW (2015). To adjust or not to adjust? Sensitivity analysis of M-bias and butterfly-bias. Journal of Causal Inference, 3(1), 41–57. [ Google Scholar ]
• Fox J (2006). Structural equation modeling with the sem package in R. Structural Equation Modeling, 13, 465–486. [ Google Scholar ]
• Hahn J, Todd P, & Van der Klaauw W (2001). Identification and estimation of treatment effects with a regression–discontinuity design. Econometrica, 69(1), 201–209. [ Google Scholar ]
• Hansen BB (2004). Full matching in an observational study of coaching for the SAT. Journal of the American Statistical Association, 99, 609–618. [ Google Scholar ]
• Hansen BB, & Klopfer SO (2006). Optimal full matching and related designs via network flows. Journal of Computational and Graphical Statistics, 15, 609–627. [ Google Scholar ]
• Ho D, Imai K, King G, & Stuart EA (2011). MatchIt: Nonparametric preprocessing for parametric causal inference. Journal of Statistical Software, 42(8), 1–28. Retrieved from http://www.jstatsoft.org/v42/i08/ [ Google Scholar ]
• Holland PW (1986). Statistics and causal inference. Journal of the American Statistical Association, 81, 945–960. [ Google Scholar ]
• Holland PW (1988). Causal inference, path analysis and recursive structural equations models. ETS Research Report Series. doi: 10.1002/j.2330-8516.1988.tb00270.x [ DOI ] [ Google Scholar ]
• Horvitz DG, & Thompson DJ (1952). A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association, 47, 663–685. [ Google Scholar ]
• Imai K, Keele L, Tingley D, & Yamamoto T (2011). Unpacking the black box of causality: Learning about causal mechanisms from experimental and observational studies. American Political Science Review, 105, 765–789. [ Google Scholar ]
• Imbens GW, & Lemieux T (2008). Regression discontinuity designs: A guide to practice. Journal of Econometrics, 142, 615–635. [ Google Scholar ]
• Imbens GW, & Rubin DB (2015). Causal inference in statistics, social, and biomedical sciences. New York, NY: Cambridge University Press. [ Google Scholar ]
• Kazdin AE (2011). Single-case research designs: Methods for clinical and applied settings. New York, NY: Oxford University Press. [ Google Scholar ]
• Keller B, Kim JS, & Steiner PM (2015). Neural networks for propensity score estimation: Simulation results and recommendations In van der Ark LA, Bolt DM, Chow S-M, Douglas JA, & Wang W-C (Eds.), Quantitative psychology research (pp. 279–291). New York, NY: Springer. [ Google Scholar ]
• Lechner M (2011). The estimation of causal effects by difference-in-difference methods. Foundations and Trends in Econometrics, 4, 165–224. [ Google Scholar ]
• Lee DS, & Lemieux T (2010). Regression discontinuity designs in economics. Journal of Economic Literature, 48, 281–355. [ Google Scholar ]
• McCaffrey DF, Ridgeway G, & Morral AR (2004). Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychological Methods, 9, 403–425. [ DOI ] [ PubMed ] [ Google Scholar ]
• McCrary J (2008). Manipulation of the running variable in the regression discontinuity design: A density test. Journal of Econometrics, 142, 698–714. [ Google Scholar ]
• Nichols A (2007). rd: Stata modules for regression discontinuity estimation. Retrieved from http://ideas.repec.org/c/boc/bocode/s456888.html
• Pearl J (2009). C ausality: Models, reasoning, and inference (2nd ed.). New York, NY: Cambridge University Press. [ Google Scholar ]
• Pearl J (2010). On a class of bias-amplifying variables that endanger effect estimates In Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence (pp. 425–432). Corvallis, OR: Association for Uncertainty in Artificial Intelligence. [ Google Scholar ]
• Robins JM, & Rotnitzky A (1995). Semiparametric efficiency in multivariate regression models with missing data. Journal of the American Statistical Association, 90(429), 122–129. [ Google Scholar ]
• Rosenbaum PR (2002). Observational studies. New York, NY: Springer. [ Google Scholar ]
• Rosenbaum PR, & Rubin DB (1983). The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1), 41–55. [ Google Scholar ]
• Schafer JL, & Kang J (2008). Average causal effects from nonrandomized studies: A practical guide and simulated example. Psychological Methods, 13, 279–313. [ DOI ] [ PubMed ] [ Google Scholar ]
• Sekhon JS (2011). Multivariate and propensity score matching software with automated balance optimization: The matching package for R. Journal of Statistical Software, 42(7), 1–52. [ Google Scholar ]
• Shadish WR, Cook TD, & Campbell DT (2002). Experimental and quasi-experimental designs for generalized causal inference. Boston, MA: Houghton-Mifflin. [ Google Scholar ]
• Somers M, Zhu P, Jacob R, & Bloom H (2013). The validity and precision of the comparative interrupted time series design and the difference-in-difference design in educational evaluation (MDRC working paper in research methodology). New York, NY: MDRC. [ Google Scholar ]
• StataCorp. (2015). Stata treatment-effects reference manual: Potential outcomes/counterfactual outcomes. College Station, TX: Stata Press; Retrieved from http://www.stata.com/manuals14/te.pdf [ Google Scholar ]
• Steiner PM, & Cook D (2013). Matching and propensity scores In Little T (Ed.), The Oxford handbook of quantitative methods in psychology (Vol. 1, pp. 237–259). New York, NY: Oxford University Press. [ Google Scholar ]
• Steiner PM, Cook TD, Li W, & Clark MH (2015). Bias reduction in quasi-experiments with little selection theory but many covariates. Journal of Research on Educational Effectiveness, 8, 552–576. [ Google Scholar ]
• Steiner PM, Cook TD, & Shadish WR (2011). On the importance of reliable covariate measurement in selection bias adjustments using propensity scores. Journal of Educational and Behavioral Statistics, 36, 213–236. [ Google Scholar ]
• Steiner PM, & Kim Y (in press). The mechanics of omitted variable bias: Bias amplification and cancellation of offsetting biases. Journal of Causal Inference. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Steiner PM, Kim Y, Hall CE, & Su D (2015). Graphical models for quasi-experimental designs. Sociological Methods & Research. Advance online publication. doi: 10.1177/0049124115582272 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• West SG, Biesanz JC, & Pitts SC (2000). Causal inference and generalization in field settings: Experimental and quasi-experimental designs In Reis HT & Judd CM (Eds.), Handbook of research methods in social and personality psychology (pp. 40–84). New York, NY: Cambridge University Press. [ Google Scholar ]
• Wing C, & Cook TD (2013). Strengthening the regression discontinuity design using additional design elements: A within-study comparison. Journal of Policy Analysis and Management, 32, 853–877. [ Google Scholar ]
• Wong M, Cook TD, & Steiner PM (2009). No Child Left Behind: An interim evaluation of its effects on learning using two interrupted time series each with its own non-equivalent comparison series (Working Paper No. WP-09–11). Evanston, IL: Institute for Policy Research, Northwestern University. [ Google Scholar ]
• Wong VC, Wing C, Steiner PM, Wong M, & Cook TD (2012). Research designs for program evaluation. Handbook of Psychology, 2, 316–341. [ Google Scholar ]
• Wooldridge J (2012). Introductory econometrics: A modern approach (5th ed.). Mason, OH: South-Western Cengage Learning. [ Google Scholar ]
• View on publisher site
• PDF (687.1 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Perspective
• Published: 14 January 2021

Quantifying causality in data science with quasi-experiments

• Tony Liu 1 ,
• Lyle Ungar 1 &
• Konrad Kording   ORCID: orcid.org/0000-0001-8408-4499 2 , 3  

Nature Computational Science volume  1 ,  pages 24–32 ( 2021 ) Cite this article

13k Accesses

21 Citations

43 Altmetric

Metrics details

• Computational science
• Computer science

Estimating causality from observational data is essential in many data science questions but can be a challenging task. Here we review approaches to causality that are popular in econometrics and that exploit (quasi) random variation in existing data, called quasi-experiments, and show how they can be combined with machine learning to answer causal questions within typical data science settings. We also highlight how data scientists can help advance these methods to bring causal estimation to high-dimensional data from medicine, industry and society.

This is a preview of subscription content, access via your institution

Access options

Similar content being viewed by others

Stable learning establishes some common ground between causal inference and machine learning

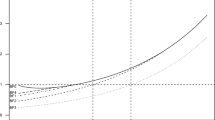
Simple nested Bayesian hypothesis testing for meta-analysis, Cox, Poisson and logistic regression models

Causal inference on human behaviour

Code availability.

We provide interactive widgets of Figs. 2 – 4 in a Jupyter Notebook hosted in a public GitHub repository ( https://github.com/tliu526/causal-data-science-perspective ) and served through Binder (see link in the GitHub repository).

van Dyk, D. et al. ASA statement on the role of statistics in data science. Amstat News https://magazine.amstat.org/blog/2015/10/01/asa-statement-on-the-role-of-statistics-in-data-science/ (2015).

Pearl, J. The seven tools of causal inference, with reflections on machine learning. Commun. ACM 62 , 54–60 (2019).

Article   Google Scholar  

Hernán, M. A., Hsu, J. & Healy, B. Data science is science’s second chance to get causal inference right: a classification of data science tasks. Chance 32 , 42–49 (2019).

Caruana, R. et al. Intelligible models for healthcare: predicting pneumonia risk and hospital 30-day readmission. In Proc. 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1721–1730 (ACM Press, 2015); https://doi.org/10.1145/2783258.2788613

Finkelstein, A. et al. The Oregon health insurance experiment: evidence from the first year. Q. J. Econ. 127 , 1057–1106 (2012).

Forney, A., Pearl, J. & Bareinboim, E. Counterfactual data-fusion for online reinforcement learners. In International Conference on Machine Learning (eds. Precup, D. & Teh, Y. W.) 1156–1164 (PMLR, 2017).

Thomas, P. S. & Brunskill, E. Data-efficient off-policy policy evaluation for reinforcement learning. International Conference on Machine Learning (eds. Balcan, M. F. & Weinberger, K.) 2139–2148 (PMLR, 2016).

Athey, S. & Wager, S. Policy learning with observational data. Econometrica (in the press).

Angrist, J. D. & Pischke, J.-S. Mostly Harmless Econometrics: An Empiricist’s Companion (Princeton Univ. Press, 2008).

Imbens, G. & Rubin, D. B. Causal Inference: For Statistics, Social and Biomedical Sciences: An Introduction (Cambridge Univ. Press 2015).

Pearl, J. Causality (Cambridge Univ. Press, 2009).

Hernán, M. A. & Robins, J. M. Causal Inference: What If (Chapman & Hall/CRC, 2020).

Pearl, J. Causal inference in statistics: an overview. Stat. Surv. 3 , 96–146 (2009).

Article   MathSciNet   MATH   Google Scholar  

Peters, J., Janzing, D. & Schölkopf, B. Elements of Causal Inference: Foundations and Learning Algorithms (MIT Press, 2017).

Rosenbaum, P. R. & Rubin, D. B. The central role of the propensity score in observational studies for causal effects. Biometrika 70 , 41–55 (1983).

Chernozhukov, V. et al. Double/debiased machine learning for treatment and structural parameters. Econ. J. 21 , C1–C68 (2018).

MathSciNet   Google Scholar  

Spirtes, P., Glymour, C. N. & Scheines, R. Causation, Prediction, and Search (MIT Press, 2000).

Schölkopf, B. Causality for machine learning. Preprint at https://arxiv.org/abs/1911.10500 (2019).

Mooij, J. M., Peters, J., Janzing, D., Zscheischler, J. & Schölkopf, B. Distinguishing cause from effect using observational data: methods and benchmarks. J. Mach. Learn. Res. 17 , 1103–1204 (2016).

MathSciNet   MATH   Google Scholar  

Huang, B. et al. Causal discovery from heterogeneous/nonstationary data. J. Mach. Learn. Res. 21 , 1–53 (2020).

Wang, Y. & Blei, D. M. The blessings of multiple causes. J. Am. Stat. Assoc. 114 , 1574–1596 (2019).

Leamer, E. E. Let’s take the con out of econometrics. Am. Econ. Rev. 73 , 31–43 (1983).

Google Scholar  

Angrist, J. D. & Pischke, J.-S. The credibility revolution in empirical economics: how better research design is taking the con out of econometrics. J. Econ. Perspect. 24 , 3–30 (2010).

Angrist, J. D. & Krueger, A. B. Instrumental variables and the search for identification: from supply and demand to natural experiments. J. Econ. Perspect. 15 , 69–85 (2001).

Angrist, J. D. & Krueger, A. B. Does compulsory school attendance affect schooling and earnings? Q. J. Econ. 106 , 979–1014 (1991).

Wooldridge, J. M. Econometric Analysis of Cross Section and Panel Data (MIT Press, 2010).

Angrist, J. D., Imbens, G. W. & Krueger, A. B. Jackknife instrumental variables estimation. J. Appl. Econom. 14 , 57–67 (1999).

Newhouse, J. P. & McClellan, M. Econometrics in outcomes research: the use of instrumental variables. Annu. Rev. Public Health 19 , 17–34 (1998).

Imbens, G. Potential Outcome and Directed Acyclic Graph Approaches to Causality: Relevance for Empirical Practice in Economics Working Paper No. 26104 (NBER, 2019); https://doi.org/10.3386/w26104

Hanandita, W. & Tampubolon, G. Does poverty reduce mental health? An instrumental variable analysis. Soc. Sci. Med. 113 , 59–67 (2014).

Angrist, J. D., Graddy, K. & Imbens, G. W. The interpretation of instrumental variables estimators in simultaneous equations models with an application to the demand for fish. Rev. Econ. Stud. 67 , 499–527 (2000).

Article   MATH   Google Scholar  

Thistlethwaite, D. L. & Campbell, D. T. Regression-discontinuity analysis: an alternative to the ex post facto experiment. J. Educ. Psychol. 51 , 309–317 (1960).

Fine, M. J. et al. A prediction rule to identify low-risk patients with community-acquired pneumonia. N. Engl. J. Med. 336 , 243–250 (1997).

Lee, D. S. & Lemieux, T. Regression discontinuity designs in economics. J. Econ. Lit. 48 , 281–355 (2010).

Cattaneo, M. D., Idrobo, N. & Titiunik, R. A Practical Introduction to Regression Discontinuity Designs (Cambridge Univ. Press, 2019).

Imbens, G. & Kalyanaraman, K. Optimal Bandwidth Choice for the Regression Discontinuity Estimator Working Paper No. 14726 (NBER, 2009); https://doi.org/10.3386/w14726

Calonico, S., Cattaneo, M. D. & Titiunik, R. Robust data-driven inference in the regression-discontinuity design. Stata J. 14 , 909–946 (2014).

McCrary, J. Manipulation of the running variable in the regression discontinuity design: a density test. J. Econ. 142 , 698–714 (2008).

Imbens, G. & Lemieux, T. Regression discontinuity designs: a guide to practice. J. Economet. 142 , 615–635 (2008).

NCI funding policy for RPG awards. NIH: National Cancer Institute https://deainfo.nci.nih.gov/grantspolicies/finalfundltr.htm (2020).

NIAID paylines. NIH: National Institute of Allergy and Infectious Diseases http://www.niaid.nih.gov/grants-contracts/niaid-paylines (2020).

Keele, L. J. & Titiunik, R. Geographic boundaries as regression discontinuities. Polit. Anal. 23 , 127–155 (2015).

Card, D. & Krueger, A. B. Minimum Wages and Employment: A Case Study of the Fast Food Industry in New Jersey and Pennsylvania Working Paper No. 4509 (NBER, 1993); https://doi.org/10.3386/w4509

Ashenfelter, O. & Card, D. Using the Longitudinal Structure of Earnings to Estimate the Effect of Training Programs Working Paper No. 1489 (NBER, 1984); https://doi.org/10.3386/w1489

Angrist, J. D. & Krueger, A. B. in Handbook of Labor Economics Vol. 3 (eds. Ashenfelter, O. C. & Card, D.) 1277–1366 (Elsevier, 1999).

Athey, S. & Imbens, G. W. Identification and inference in nonlinear difference-in-differences models. Econometrica 74 , 431–497 (2006).

Abadie, A. Semiparametric difference-in-differences estimators. Rev. Econ. Stud. 72 , 1–19 (2005).

Lu, C., Nie, X. & Wager, S. Robust nonparametric difference-in-differences estimation. Preprint at https://arxiv.org/abs/1905.11622 (2019).

Besley, T. & Case, A. Unnatural experiments? estimating the incidence of endogenous policies. Econ. J. 110 , 672–694 (2000).

Nunn, N. & Qian, N. US food aid and civil conflict. Am. Econ. Rev. 104 , 1630–1666 (2014).

Christian, P. & Barrett, C. B. Revisiting the Effect of Food Aid on Conflict: A Methodological Caution (The World Bank, 2017); https://doi.org/10.1596/1813-9450-8171 .

Angrist, J. & Imbens, G. Identification and Estimation of Local Average Treatment Effects Technical Working Paper No. 118 (NBER, 1995); https://doi.org/10.3386/t0118

Hahn, J., Todd, P. & Van der Klaauw, W. Identification and estimation of treatment effects with a regression-discontinuity design. Econometrica 69 , 201–209 (2001).

Angrist, J. & Rokkanen, M. Wanna Get Away? RD Identification Away from the Cutoff Working Paper No. 18662 (NBER, 2012); https://doi.org/10.3386/w18662

Rothwell, P. M. External validity of randomised controlled trials: “To whom do the results of this trial apply?”. The Lancet 365 , 82–93 (2005).

Rubin, D. B. For objective causal inference, design trumps analysis. Ann. Appl. Stat. 2 , 808–840 (2008).

Chaney, A. J. B., Stewart, B. M. & Engelhardt, B. E. How algorithmic confounding in recommendation systems increases homogeneity and decreases utility. In Proc. 12th ACM Conference on Recommender Systems 224–232 (Association for Computing Machinery, 2018); https://doi.org/10.1145/3240323.3240370 .

Sharma, A., Hofman, J. M. & Watts, D. J. Estimating the causal impact of recommendation systems from observational data. In Proc. Sixteenth ACM Conference on Economics and Computation 453–470 (Association for Computing Machinery, 2015); https://doi.org/10.1145/2764468.2764488

Lawlor, D. A., Harbord, R. M., Sterne, J. A. C., Timpson, N. & Smith, G. D. Mendelian randomization: using genes as instruments for making causal inferences in epidemiology. Stat. Med. 27 , 1133–1163 (2008).

Article   MathSciNet   Google Scholar  

Zhao, Q., Chen, Y., Wang, J. & Small, D. S. Powerful three-sample genome-wide design and robust statistical inference in summary-data Mendelian randomization. Int. J. Epidemiol. 48 , 1478–1492 (2019).

Moscoe, E., Bor, J. & Bärnighausen, T. Regression discontinuity designs are underutilized in medicine, epidemiology, and public health: a review of current and best practice. J. Clin. Epidemiol. 68 , 132–143 (2015).

Blake, T., Nosko, C. & Tadelis, S. Consumer heterogeneity and paid search effectiveness: a large-scale field experiment. Econometrica 83 , 155–174 (2015).

Dimick, J. B. & Ryan, A. M. Methods for evaluating changes in health care policy: the difference-in-differences approach. JAMA 312 , 2401–2402 (2014).

Kallus, N., Puli, A. M. & Shalit, U. Removing hidden confounding by experimental grounding. Adv. Neural Inf. Process. Syst. 31 , 10888–10897 (2018).

Zhang, J. & Bareinboim, E. Markov Decision Processes with Unobserved Confounders: A Causal Approach. Technical Report (R-23) (Columbia CausalAI Laboratory, 2016).

Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518 , 529–533 (2015).

Lansdell, B., Triantafillou, S. & Kording, K. Rarely-switching linear bandits: optimization of causal effects for the real world. Preprint at https://arxiv.org/abs/1905.13121 (2019).

Adadi, A. & Berrada, M. Peeking inside the black-box: a survey on explainable artificial intelligence (XAI). IEEE Access 6 , 52138–52160 (2018).

Zhao, Q. & Hastie, T. Causal interpretations of black-box models. J. Bus. Econ. Stat. 39 , 272–281 (2021).

Moraffah, R., Karami, M., Guo, R., Raglin, A. & Liu, H. Causal interpretability for machine learning—problems, methods and evaluation. ACM SIGKDD Explor. Newsl. 22 , 18–33 (2020).

Ribeiro, M. T., Singh, S. & Guestrin, C. ‘Why should I trust you?’: Explaining the predictions of any classifier. In Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 1135–1144 (Association for Computing Machinery, 2016); https://doi.org/10.1145/2939672.2939778

Mothilal, R. K., Sharma, A. & Tan, C. Explaining machine learning classifiers through diverse counterfactual explanations. In Proc. 2020 Conference on Fairness, Accountability, and Transparency 607–617 (Association for Computing Machinery, 2020); https://doi.org/10.1145/3351095.3372850

Hooker, G. & Mentch, L. Please stop permuting features: an explanation and alternatives. Preprint at https://arxiv.org/abs/1905.03151 (2019).

Mullainathan, S. & Spiess, J. Machine learning: an applied econometric approach. J. Econ. Perspect. 31 , 87–106 (2017).

Belloni, A., Chen, D., Chernozhukov, V. & Hansen, C. Sparse models and methods for optimal instruments with an application to eminent domain. Econometrica 80 , 2369–2429 (2012).

Singh, R., Sahani, M. & Gretton, A. Kernel instrumental variable regression. Adv. Neural Inf. Process. Syst. 32 , 4593–4605 (2019).

Hartford, J., Lewis, G., Leyton-Brown, K. & Taddy, M. Deep IV: a flexible approach for counterfactual prediction. In Proc. 34th International Conference on Machine Learning Vol. 70 (eds. Precup, D. & Teh Y. W.) 1414–1423 (JMLR.org, 2017).

Athey, S., Bayati, M., Doudchenko, N., Imbens, G. & Khosravi, K. Matrix Completion Methods for Causal Panel Data Models Working Paper No. 25132 (NBER, 2018); https://doi.org/10.3386/w25132

Athey, S., Bayati, M., Imbens, G. & Qu, Z. Ensemble methods for causal effects in panel data settings. AEA Pap. Proc. 109 , 65–70 (2019).

Kennedy, E. H., Balakrishnan, S. & G’Sell, M. Sharp instruments for classifying compliers and generalizing causal effects. Ann. Stat. 48 , 2008–2030 (2020).

Kallus, N. Classifying treatment responders under causal effect monotonicity. In Proc. 36th International Conference on Machine Learning Vol. 97 (eds. Chaudhuri, K. & Salakhutdniov, R.) 3201–3210 (PMLR, 2019).

Li, A. & Pearl, J. Unit selection based on counterfactual logic. In Proc. Twenty-Eighth International Joint Conference on Artificial Intelligence (ed. Kraus, S.) 1793–1799 (International Joint Conferences on Artificial Intelligence Organization, 2019); https://doi.org/10.24963/ijcai.2019/248

Dong, Y. & Lewbel, A. Identifying the effect of changing the policy threshold in regression discontinuity models. Rev. Econ. Stat. 97 , 1081–1092 (2015).

Marinescu, I. E., Triantafillou, S. & Kording, K. Regression discontinuity threshold optimization. SSRN https://doi.org/10.2139/ssrn.3333334 (2019).

Varian, H. R. Big data: new tricks for econometrics. J. Econ. Perspect. 28 , 3–28 (2014).

Athey, S. & Imbens, G. W. Machine learning methods that economists should know about. Annu. Rev. Econ. 11 , 685–725 (2019).

Hudgens, M. G. & Halloran, M. E. Toward causal inference with interference. J. Am. Stat. Assoc. 103 , 832–842 (2008).

Graham, B. & de Paula, A. The Econometric Analysis of Network Data (Elsevier, 2019).

Varian, H. R. Causal inference in economics and marketing. Proc. Natl. Acad. Sci. USA 113 , 7310–7315 (2016).

Marinescu, I. E., Lawlor, P. N. & Kording, K. P. Quasi-experimental causality in neuroscience and behavioural research. Nat. Hum. Behav. 2 , 891–898 (2018).

Abadie, A. & Cattaneo, M. D. Econometric methods for program evaluation. Annu. Rev. Econ. 10 , 465–503 (2018).

Huang, A. & Levinson, D. The effects of daylight saving time on vehicle crashes in Minnesota. J. Safety Res. 41 , 513–520 (2010).

Lepperød, M. E., Stöber, T., Hafting, T., Fyhn, M. & Kording, K. P. Inferring causal connectivity from pairwise recordings and optogenetics. Preprint at bioRxiv https://doi.org/10.1101/463760 (2018).

Bor, J., Moscoe, E., Mutevedzi, P., Newell, M.-L. & Bärnighausen, T. Regression discontinuity designs in epidemiology. Epidemiol. Camb. Mass 25 , 729–737 (2014).

Chen, Y., Ebenstein, A., Greenstone, M. & Li, H. Evidence on the impact of sustained exposure to air pollution on life expectancy from China’s Huai River policy. Proc. Natl. Acad. Sci. USA 110 , 12936–12941 (2013).

Lansdell, B. J. & Kording, K. P. Spiking allows neurons to estimate their causal effect. Preprint at bioRxiv https://doi.org/10.1101/253351 (2019).

Patel, M. S. et al. Association of the 2011 ACGME resident duty hour reforms with mortality and readmissions among hospitalized medicare patients. JAMA 312 , 2364–2373 (2014).

Rishika, R., Kumar, A., Janakiraman, R. & Bezawada, R. The effect of customers’ social media participation on customer visit frequency and profitability: an empirical investigation. Inf. Syst. Res. 24 , 108–127 (2012).

Butsic, V., Lewis, D. J., Radeloff, V. C., Baumann, M. & Kuemmerle, T. Quasi-experimental methods enable stronger inferences from observational data in ecology. Basic Appl. Ecol. 19 , 1–10 (2017).

Download references

Acknowledgements

We thank R. Ladhania and B. Lansdell for their comments and suggestions on this work. We acknowledge support from National Institutes of Health grant R01-EB028162. T.L. is supported by National Institute of Mental Health grant R01-MH111610.

Author information

Authors and affiliations.

Department of Computer and Information Science, University of Pennsylvania, Philadelphia, PA, USA

Tony Liu & Lyle Ungar

Department of Bioengineering, University of Pennsylvania, Philadelphia, PA, USA

Konrad Kording

Department of Neuroscience, University of Pennsylvania, Philadelphia, PA, USA

You can also search for this author in PubMed   Google Scholar

Contributions

T.L. helped write and prepare the manuscript. L.U. and K.K. jointly supervised this work and helped write the manuscript. All authors discussed the structure and direction of the manuscript throughout its development.

Corresponding author

Correspondence to Konrad Kording .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Peer review information Fernando Chirigati was the primary editor on this Perspective and managed its editorial process and peer review in collaboration with the rest of the editorial team. Nature Computational Science thanks Jesper Tegnér and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Liu, T., Ungar, L. & Kording, K. Quantifying causality in data science with quasi-experiments. Nat Comput Sci 1 , 24–32 (2021). https://doi.org/10.1038/s43588-020-00005-8

Download citation

Received : 14 August 2020

Accepted : 30 November 2020

Published : 14 January 2021

Issue Date : January 2021

DOI : https://doi.org/10.1038/s43588-020-00005-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Gendered beliefs about mathematics ability transmit across generations through children’s peers.

Nature Human Behaviour (2022)

Integrating explanation and prediction in computational social science

• Jake M. Hofman
• Duncan J. Watts
• Tal Yarkoni

Nature (2021)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

The Limitations of Quasi-Experimental Studies, and Methods for Data Analysis When a Quasi-Experimental Research Design Is Unavoidable

Affiliation.

• 1 Dept. of Clinical Psychopharmacology and Neurotoxicology, National Institute of Mental Health and Neurosciences, Bengaluru, Karnataka, India.
• PMID: 34584313
• PMCID: PMC8450731
• DOI: 10.1177/02537176211034707

A quasi-experimental (QE) study is one that compares outcomes between intervention groups where, for reasons related to ethics or feasibility, participants are not randomized to their respective interventions; an example is the historical comparison of pregnancy outcomes in women who did versus did not receive antidepressant medication during pregnancy. QE designs are sometimes used in noninterventional research, as well; an example is the comparison of neuropsychological test performance between first degree relatives of schizophrenia patients and healthy controls. In QE studies, groups may differ systematically in several ways at baseline, itself; when these differences influence the outcome of interest, comparing outcomes between groups using univariable methods can generate misleading results. Multivariable regression is therefore suggested as a better approach to data analysis; because the effects of confounding variables can be adjusted for in multivariable regression, the unique effect of the grouping variable can be better understood. However, although multivariable regression is better than univariable analyses, there are inevitably inadequately measured, unmeasured, and unknown confounds that may limit the validity of the conclusions drawn. Investigators should therefore employ QE designs sparingly, and only if no other option is available to answer an important research question.

Keywords: Quasi-experimental study; confounding variables; multivariable regression; research design; univariable analysis.

© 2021 Indian Psychiatric Society - South Zonal Branch.

Skip to content

Get Revising

Join get revising, already a member.

Quasi experiment

• Created by: Sarah18
• Created on: 21-10-13 21:51
• Experiments

No comments have yet been made

Similar Psychology resources:

Methods in AS psychology 0.0 / 5

Strengths and limitations of natural + quasi experiments 0.0 / 5

Types of Experiments 0.0 / 5

Research Methods - Types of Experiment 5.0 / 5 based on 1 rating

Research methods 3.0 / 5 based on 2 ratings

Natural And Quasi-experiments 0.0 / 5

Advantages and Disadvantages of Experiment Types 5.0 / 5 based on 1 rating Teacher recommended

Research methods 1.5 / 5 based on 2 ratings

Pyschology 3.0 / 5 based on 1 rating

AS RESEARCH METHODS 0.0 / 5

Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

Loading metrics

Open Access

Study Protocol

The basic income for care leavers in Wales pilot evaluation: Protocol of a quasi-experimental evaluation

Roles Conceptualization, Funding acquisition, Methodology, Writing – original draft

* E-mail: [email protected]

Affiliation Cardiff University, School of Social Sciences, Cardiff, United Kingdom

Affiliation Kings College London, The Policy Institute, London, United Kingdom

Affiliation University of Oxford, Nuffield Department for Primary Care Health Sciences, Oxford, United Kingdom

Roles Funding acquisition, Methodology, Writing – review & editing

Affiliation University of York, Health Sciences, York, United Kingdom

Roles Funding acquisition, Writing – review & editing

Affiliation Social Work, Education & Community Wellbeing, Northumbria University, Newcastle, United Kingdom

Affiliation Centre for Homelessness Impact, London, United Kingdom

Roles Data curation

Roles Data curation, Writing – original draft

Roles Data curation, Writing – review & editing

• David Westlake, 
• Sally Holland, 
• Michael Sanders, 
• Elizabeth Schroeder, 
• Kate E. Pickett, 
• Matthew Johnson, 
• Stavros Petrou, 
• Rod Hick, 
• Louise Roberts, 

• Published: October 18, 2024
• https://doi.org/10.1371/journal.pone.0303837
• Reader Comments

This study will evaluate the Basic Income for Care Leavers in Wales pilot (BIP), which is the most generous basic income scheme in the world. A cohort of care-experienced young people who become aged 18 during a 12-month enrolment period (July 2022-June 2023) are receiving £1,600 (before tax) per month for two years, and the Welsh Government intends this to have a range of benefits. This evaluation will examine the impact of BIP, the implementation of the pilot and how it is experienced, and its value for money.

The study is a theory-based quasi-experimental evaluation, and the design and methods are informed by ongoing co-production with care-experienced young people. We will estimate the impact of BIP on participants using self-reported survey data and routinely collected administrative data. This will include outcomes across a range of domains, including psychological wellbeing, physical and mental health, financial impact, education, training and volunteering. Comparisons between temporal (Welsh) and geographical (English, using administrative data) controls will be done using coarsened exact matching and difference in differences analysis. The process evaluation will examine how BIP is implemented and experienced, primarily through monitoring data (quantitative) and interview, observational, and focus group data (qualitative). The economic evaluation will take a public sector and a societal perspective to identify, measure and value the costs and outcomes of BIP, and to synthesise the evidence to inform a social cost-benefit analysis at 24 months post-intervention.

BIP is unusual in that it targets a wide range of outcomes and is available to an entire national cohort of participants. The evaluation also has several practical constraints. Therefore, the study will use a range of methods and triangulate between different analyses to assess how successful it is. Findings will inform policy in relation to care leavers, social security and basic income studies worldwide.

Citation: Westlake D, Holland S, Sanders M, Schroeder E, Pickett KE, Johnson M, et al. (2024) The basic income for care leavers in Wales pilot evaluation: Protocol of a quasi-experimental evaluation. PLoS ONE 19(10): e0303837. https://doi.org/10.1371/journal.pone.0303837

Editor: Cathryn Knight, University of Bristol, UNITED KINGDOM OF GREAT BRITAIN AND NORTHERN IRELAND

Received: December 15, 2023; Accepted: April 29, 2024; Published: October 18, 2024

Copyright: © 2024 Westlake et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Data Availability: No datasets were generated or analysed during the current study. All relevant data from this study will be made available upon study completion.

Funding: This study was funded by the Welsh Government. The ActEarly UK Prevention Research Partnership Consortium (Project Reference: MR/S037527/1) supported Professor Kate E. Pickett’s involvement in the study. Health and Care Research Wales provided infrastructure funding that supports the study at CASCADE, Cardiff University.

Competing interests: I have read the journal’s policy and the authors of this manuscript have the following competing interests:David Westlake is a provider of supported lodging for care leavers in Wales, which is a not-for-profit local authority service that is adjacent to the scheme being evaluated in this study. Louise Roberts is a Trustee for Voices from Care, Cymru, a not-for-profit grassroots organisation that was involved in the development and ongoing delivery of the project as government consultees.

Abbreviations: CSC, Children’s social care; EE, Economic evaluation; IPE, Implementation and process evaluation; DSA, Data sharing agreement; NPD, National pupil database; LA, Local authority; BIP, Basic Income for Care Leavers in Wales Pilot; YLBC, Your life beyond care survey

Introduction

Background and rationale.

This study will evaluate the Basic Income for Care Leavers in Wales pilot (BIP). The BIP aims to improve outcomes for care experienced young adults across many areas of their lives, and follows other pilots and programmes around the world which have tested the efficacy of basic incomes for disadvantaged groups [ 1 ]. The BIP is inspired by research and scholarship on Universal Basic Income (UBI) and is a unique example of a basic income experiment. This is because of both the level of income participants receive and the fact that a whole national age cohort of care leavers is eligible. All care-experienced young people turning 18 during the enrolment period (12 months; July 2022 – June 2023) are eligible to receive a monthly (or twice monthly) unconditional cash transfer from the month after their 18 th birthday for 24 months. Participants receive £1,600 gross per month, which is taxed at source leaving a net amount of £1,280 a month. Some participants may be able to claim some tax back depending on their individual circumstances. These figures were based broadly on the Real Living Wage [ 2 ] for a full-time employee in 2021/22 (the time of the policy development), and compares to a National Minimum Wage for 18 year olds at the same time of £1,100 per month. This makes this pilot the most generous scheme of its kind worldwide [ 3 ]. Similar schemes have targeted homelessness, unemployment, and various other social issues. However, at the time of announcement the BIP was only the second to target care leavers. The first to target this population was a pilot in Santa Clara county, California, USA, which targeted foster care leavers and is discussed below. There are now a series of pilots underway across California with foster care leavers, the definition of which appears to include young people who have been in a range of care settings (not just what UK readers would recognise as ‘foster care’).

The Welsh policy and practice context.

Wales is a country within the United Kingdom (UK) and has its own devolved administration. The Welsh Government designed the BIP to serve policy goals set out in the Programme for Government 2021-26 and the Wellbeing of Future Generations (Wales) Act (2015), including ‘a healthy Wales’, ‘a more equal Wales’ and ‘a Wales of more cohesive communities’ [ 4 ]. In order to design the BIP the Welsh Government set up a governance structure comprising three groups: the Steering Group; the Operations Group; and the Technical Advisory Group (TAG). A range of government officials and experts sit on these groups, with the TAG being chaired by Professor Sir Michael Marmot. BIP also incorporates a human rights approach, particularly the socio-economic duty (Section 1 of the Equality Act) which was commenced in Wales in 2021.

The rationale for targeting care leavers was based on evidence in Wales [ 5 ], the UK [ 6 ] and internationally [ 7 ] that care-experienced young people often face a precarious period in the years after their 18 th birthday. A myriad of challenges include a higher likelihood than the general population of experiencing poverty and precarious housing situations [ 8 ], and over-representation in the criminal justice system in England and Wales (both as victims and perpetrators) [ 9 ]. Early childhood trauma, sometimes compounded by instability in care after becoming looked-after, can lead to a greater propensity for poor mental and physical health [ 10 ]. Notwithstanding these wide-ranging challenges, many care-experienced young people achieve successes in education, employment and contribution to their communities [ 11 ].

Risks to children tend to be greatest before and after they are in care, and there is evidence that the benefits many children gain from being in care risk being undone in the years after they leave [ 12 ]. The outcomes for children in public care are generally considered to be poor. This has contributed to a focus on reducing the number of children in care: a goal that is made explicit in the provisions of the current Children and Young Persons Bill. Yet while children in care do less well than most children on a range of measures, such comparisons do not disentangle the extent to which these difficulties pre-dated care and the specific impact of care on child welfare. Moreover, the service offer for care leavers in Wales has improved in recent years, with more options and support for young people reaching adulthood. It is encouraging to note that the most common housing destination for care leavers at 18 is now to stay with their foster carers in a ‘When I’m Ready’ arrangement [ 13 ]. Other welcome advances to tackle poverty amongst care leavers in Wales include exemption from paying Council Tax [ 14 ] and the St David’s Fund, which is administered by local authorities and designed to support young people who are or have been in care to gain independence [ 15 ]. These initiatives are additional to longer-standing financial support programmes such as Higher Education bursaries and cost of living payments. Alongside this progress, BIP will be seen by many as a step change in the Welsh Government’s efforts to alleviate poverty, and its associated negative impact, amongst this group.

Overview of basic income schemes.

The concept of a basic income (BI) can be traced back to ancient Greece, where Pericles (461 BC) was thought to have instigated a payment to citizens that resembled a basic income [ 16 ]. The idea has been developed and a modern definition of universal basic income offered by Van Parijs suggests it is “unconditionally paid to every member of a society [ 1 ] on an individual basis [ 2 ] without means testing and [ 3 ] without work requirement” [ 17 ]. The 1970s witnessed a few Negative Income Tax experiments in the USA, and the first pilots close to a basic income are considered to have taken place in Manitoba and Dauphin in Canada [ 18 ]. In the 21 st century there has been a sharp increase in the number of basic income trials around the world, including a few which are large-scale and a few that are government backed [ 19 ]. They are seen to serve two main purposes; to demonstrate feasibility and to evaluate effects [ 19 , 20 ]. The terms ‘pilot’, ‘experiment’ and ‘trial’ are often used interchangeably, though some have used these terms to distinguish examples of BI according to how far they adhere to theoretical ‘ideals’. Torry (2023), for example, argues only examples funded by tax revenue and with a meaningfully representative group and should be called ‘pilots’, even though this is often impractical and here are few examples of schemes that are truly universal [ 21 ]. There are however a growing number of pilot schemes aiming for community saturation, and where recipients of BI typically receive an income for which eligibility is not means-tested or dependent on (searching for) employment. (We use ‘pilot’ in the original sense of the term, and not only to mean an ‘ideal type’ scheme as suggested by Torry (2023)).

Pilot schemes vary according to their universality, conditionality, regularity, duration, how they interact with existing provision, the amounts of money offered, and how they are funded. Basic income schemes and similar programmes encompass a somewhat disparate range of arrangements, such as UBI, targeted cash transfers, social dividends, guaranteed annual income, guaranteed minimum income and negative income tax [ 1 ]. Care leavers in the BIP receive monthly or twice-monthly payments larger than that of any previous trial. Several other pilots of BI schemes have been undertaken across the world in recent years, and schemes are currently underway in numerous countries, including over 55 in the US alone [ 22 ].

A high-profile Finnish trial was delivered over the whole of 2017 and 2018 [ 23 ]. Participants were 2,000 people aged 25-58, from across Finland, who received unemployment benefits. They were selected at random to receive a tax-free payment of €560 per month, for the two-year duration of the trial. This was equivalent to, and in place of, the net level of basic unemployment benefit and basic income recipients remained eligible for other benefits (e.g., housing allowance or social assistance [ 24 ]). Participation in the trial was mandatory for the intervention group, and 178,000 unemployed individuals formed the control group [ 24 ]. The findings of the Finnish pilot have been widely debated, and are complicated by complementary interventions making attribution difficult [ 25 ]. However, the more recent and comprehensive analyses have shown that the number of days in paid employment were moderately higher for the basic income group rather than the control group, even if this cannot be fully attributed to the basic income. Additionally, the basic income group reported much higher levels of wellbeing, fewer physical and mental health issues, and higher life satisfaction than the control group [ 25 , 26 ].

Several of the ongoing schemes are particularly relevant to the BIP, in terms of their aims and target population. In the US, the California Department of Social Services are funding seven pilots across the state that target young people leaving foster care at or after 21 [ 27 ]. Almost 2,000 individuals will receive $600 to $1,200 monthly payments for between 12 to 18 months, depending on the pilot. The charity iFoster is running the biggest pilot for young people who are aging out of foster care [ 28 ]. They are providing 300 young people with $750 per month for 18 months. The pilots are due to end in 2025, and they are being evaluated by the Urban Institute, Washington DC, and the University of California, Berkeley [ 29 – 31 ].

Research on basic income.

Evidence on the impact of BI is promising but incomplete. Encouraging evidence has emerged from several recent reviews which have assessed the evidence base on the effectiveness of basic income and similar schemes [ 1 , 32 , 33 ]. These reviews show that studies have predominantly assessed impact on health, education and employment outcomes.

Gibson et al’s (2018) study was a scoping review of schemes that resemble BI, such as those associated with resource extraction dividends in Alaska, casino dividend payments for Indigenous Americans, and negative income tax schemes for low-income families. They show consistent positive impacts on health, education, entrepreneurship and crime. Specific health benefits reported include a greater uptake of health services and improved food security, nutrition, birthweight, and adult and child mental health. There is also evidence that the schemes positively impact education outcomes, with more consistent evidence for short-term (e.g. school enrolment and attendance) rather than long-term outcomes (e.g. attainment). Several studies have reported improved family relationships, more suitable housing arrangements, and reductions in adolescent and adult criminal behaviour [ 34 – 37 ]. However, there have also been some examples of adverse outcomes, such as increased substance misuse among individuals who took part [ 38 , 39 ].

Individual-level outcomes such as these have been the focus of most studies to date, and consequently outcomes at the community level have not been studied extensively. Nonetheless, there have been reports of “spill over” effects when payments are made to a large proportion of a population [ 40 , 41 ]. These include an increase in business activity and reduction in hospital admissions [ 18 , 42 , 43 ]. Positive effects were especially notable where payments were sufficient to meet basic needs and were made regularly, rather than as annual lump sums [ 44 ].

There is also evidence that the schemes have a minimal impact on labour market participation, which is important because some criticism of basic income schemes is based on the assumption that a basic income reduces labour market participation by removing incentives to work [ 45 ]. For the Finnish trial, Verho et al. [ 46 ] studied employment effects through administrative data and found no statistically significant effect on days in employment in the first year of the experiment. They found that employment effects were somewhat higher in the second year of the experiment with an increase in employment days among the intervention group (6.6 days (95% CI 1.3-11.9; p = 0.01)) [ 47 ]. Several studies utilising survey data in Finland, with a relatively low average response rate of 23%, have similarly found no significant effects on employment but greater confidence among the intervention group about the future, their ability to cope with difficult life situations, possibilities to improve their economic situations and find employment and higher levels of trust in the social security system [ 47 – 49 ].

However, the existing evidence base gives an incomplete picture because none of those schemes have been evaluated using a comprehensive range of outcomes or with methods that allow impact to be compared across studies [ 50 ]. Johnson, Johnson, Pickett and colleagues [ 51 ] suggest that impact on individual educational, economic, social and health outcomes (and attendant impact on public budgets) is likely to be significant. Their logic model ( Fig 1 ) suggests that where UBI increases the size of income, it can reduce poverty [ 52 ]; when it increases the security of income, it can reduce stress associated with threat of destitution [ 53 ]; and when it makes income more predictable, it can improve the social determinants of health, promoting longer-term thinking and behaviour that improves outcomes [ 51 ]. They have set out a generic, adaptive protocol resource to measure these impacts in basic income trials and this has informed our design [ 44 ].

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

https://doi.org/10.1371/journal.pone.0303837.g001

The highly politicised nature of basic income experiments underlines the importance of clear and comprehensive evaluation. The scheme in Ontario, that was abruptly cancelled after a change in government, illustrates the potentially negative effects of political intervention. This resulted in no evaluation findings due to a lack of data and the fact researchers are bound by confidentiality agreements [ 54 ]. Even in cases where evaluations have reported as planned, an absence of comprehensive evaluation or clarity around anticipated outcomes has sometimes left pilots and trials of basic incomes vulnerable to ‘spin’ [ 21 , 55 ]. This is partly related to how findings have been framed in the published literature. As noted above, the Finnish trial found no negative impact on labour market participation. However, evaluators failed to make clear that the expectation of critics of basic income was that it would cause a reduction in labour market participation through ‘free-riding’, and hence that no change represented a finding in favour of BI. For example, Verho et al [ 46 ] concluded “The Finnish experiment failed to produce any sizeable short-term employment effects despite offering larger improvements in employment incentives than any realistic nationwide policy could provide” (p. 27), without acknowledging this context.

A more fundamental weakness of that trial is that it failed to measure health impacts comprehensively using validated measures in ways that would have advanced evidence on the pathways and nature of causality. Similarly, the Finnish trial presented positive findings in relation to subjective wellbeing, but without baseline data, which meant these could not be attributed to BI [ 25 ]. The absence of robust and validated outcome measures that could also be used by health economists deprived the trial of key evidence on overall costs and benefits, with recent work by Johnson, Johnson, Pickett and colleagues highlighting the importance of employing comparable measures that can be used in microsimulation to model longer-term impacts at population level [ 44 ]. A weakness of the evidence base more generally is that long-term impacts have not been adequately evaluated due to the relatively short duration of most pilots [ 56 ].

The basic income for care leavers in Wales Pilot.

The level of income participants receive in the BIP makes it unique among basic income pilots, but other aspects of the scheme are also notable. In targeting care leavers, it bears similarity to the Californian pilots mentioned above. Yet, unlike these pilots, which are focussed on foster care leavers, the BIP includes young people who have been in other placement types, such as residential and kinship care. (Residential care in the UK is a form of group care for looked after children, where care is provided by teams of paid staff. Kinship care in the UK is where a looked after child resides with members of a relative, friend or other connected person – usually a member of their extended family.) Although evaluation results are not yet available from the Californian pilots, it is clear they differ in several other ways from the BIP. The Santa Clara County pilot offers older foster care leavers a lower amount for less time. The 24-year-olds involved receive $1,000 (circa £785) per month for 18 months (after the initial 12-month period was extended). It also includes fewer participants which may make it more difficult for evaluators to estimate effects robustly, though a pooled analysis of the Californian pilots may overcome this.

The aims of the BIP in Wales are also somewhat unique and demand a broad-based assessment of impact that includes a range of types of outcomes. In explaining the rationale for the Basic Income for Care Leavers in Wales pilot, the Welsh Government cites empowerment as a key aim: they hope the pilot will help care leavers feel more able and confident to make decisions, navigate challenges, and engage with their communities. Some of the more specific outcomes the Welsh Government are targeting overlap somewhat with the Californian pilots aims around poverty, equity and basic needs, but they also extend to other types of outcomes. As some of these aims are less amenable to quantification than other outcomes, it is important for the evaluation to assess these qualitatively. In a statement outlining the pilot, the Welsh Government Minister for Social Justice set out four key principles for the scheme [ 57 ]:

• Taking part in the pilot should make no participant worse off
• There should be no conditionality on income received
• The same payment should be paid to everyone
• The payment will not be altered midway through the pilot.

Unlike some other basic income pilots, most notably the Finnish trial, the BIP in Wales was not set up as a research study. The evaluation is therefore designed around an existing policy, which has various implications that we discuss herein.

The current study

Objectives..

This study is designed around three linked objectives. The primary objective is to evaluate the BIP in terms of its impact, how it is implemented and experienced, and its value for money. These are the three core areas of analysis that we will report on. The second and third objectives, respectively, are to contribute to the international evidence bases summarised above, around basic income schemes and around support for care leavers.

Research questions.

The research questions (RQs) listed below relate to the three core areas of (1) impact evaluation, (2) implementation and process evaluation (IPE), and (3) economic evaluation. Within the IPE we will explore implementation, experiences, and integration with existing services. Sets of sub-questions are emerging through discussions with our co-production group and early IPE data collection.

• RQ1: What is the impact of BIP?
• RQ2: Is the pilot implemented as intended?
• RQ3: How is the pilot experienced?
• RQ4: How does BIP fit into the overall offer for care leavers in Wales?
• RQ5: How cost effective is BIP?

Study setting.

The study will be conducted in Wales across all 22 local authority areas. Local authorities are the lowest level of elected government in Wales, and are responsible for delivering Children’s Social Care Services.

Delivery and evaluation structure.

Several parties are involved in delivery of the intervention and the evaluation. The Welsh Government is delivering the intervention in partnership with the 22 Welsh local authorities. The Welsh Government has also commissioned NEC Software Solutions UK to administer the payments. The advocacy group Voices from Care Cymru provide advice and enable co-production. Citizens Advice provide support and advice to eligible care leavers. The evaluation is being delivered by our consortium of Cardiff University (lead), King’s College London, University of Oxford, University of York, Northumbria University and the Centre for Homelessness Impact. Coram Voice, a children’s rights charity, and University of Oxford’s Rees Centre, have been separately commissioned by WG to deliver surveys (details below).

Intervention and comparator conditions.

The intervention group receive a basic income once or twice a month for two years, once they join the pilot in the month following their 18 th birthday. Those opting to receive the transfer twice monthly will receive two payments of £800 gross (£640 net); those receiving a monthly transfer receive one payment of £1,600 gross (£1,280 net). The amount of money received as a basic income was calculated by the Welsh Government to be broadly similar to the ‘Real Living Wage’ for a full-time employee in 2021/22, and it equates to £19,200 (gross) annually. This income is treated as unearned income for tax and benefit purposes and taxed at source at the basic rate of tax (20%), meaning that enrolment on the scheme may change participants’ entitlement to other benefits or liability for taxes (e.g. income tax). Individuals in the intervention group are also eligible to receive advice from the Citizens Advice Cymru, provided through the Single Advice Fund including a ‘better off’ calculation to determine whether enrolling on the pilot is financially beneficial. Comparisons will be made between the intervention group and comparator groups, including care leavers in Wales with 18 th birthdays in the 12 months following the enrolment period, and care leavers in England who are the same age as the intervention group. The comparator groups will not receive the basic income but will remain eligible for other benefits depending on their circumstances.

Strategies to improve adherence to intervention.

Take-up of the intervention is high, and 97% of those eligible for the scheme enrolled onto it [ 58 ]. The Welsh Government has worked with local authorities to support take-up and the strategies used will form part of the implementation analysis. However, the intervention is voluntary and some eligible individuals may choose not to participate. A ‘better off’ calculation is carried out for each care leaver at the point of enrollment, to ascertain whether enrolling is in their best interests financially. The IPE is designed to capture these data and will explore the reasons and consequences of not participating.

Eligibility criteria.

All young people who are ‘Category 3’ care leavers turning 18 years of age between 01 July 2022 and 30 June 2023 are eligible. Category 3 care leavers are those who are aged 18 or over who spent at least 13 weeks in the care of the local authority after the age of 14 and were still in care on their 16 th birthday (Social Services and Wellbeing (Wales) Act 2014, S.104). Children in local authority care may be looked after in foster care, residential care, kinship care or be placed with their parents under a Care Order in which parental responsibility is shared between the legal parents and the local authority.

Methodology

The study design is an impact evaluation based on a quasi-experimental design (QED), with integrated implementation and process (IPE) and economic (EE) evaluations. These are situated within a theory-based approach and a commitment to co-production, which will guide all aspects of the study. Theory-based approaches [ 59 ] are optimal for evaluating complex social interventions. We are aiming to understand whether BIP changes specific outcomes, how it may have these effects, why and for whom it may be beneficial or detrimental, and under what conditions these changes may happen [ 60 ]. Logic models that delineate the mechanisms that underpin the anticipated effects of BIP, and of basic income schemes more broadly, provide a basis for ‘theory enhancement’ using data from this evaluation. An updated programme theory and logic model will therefore be a key output.

Co-production is increasingly recognised as essential to high quality research and policy practice and is in keeping with Welsh legislation and policy, including the Social Services and Well-being Act 2014. Co-production will underpin the study and our participatory methods encompass the entire research cycle, and follow the UK Standards for Public Involvement in Research (NIHR) [ 61 ] and Wales’s Participation Standards [ 62 ]. A group of care-experienced young adults, living in a range of educational, employment and housing situations, will meet for a minimum of 16 sessions to advise the research team. Their role is to co-create research questions, data collection instruments, consider ethical and analytical questions and advise on policy and practice implications.

Impact evaluation

To measure impact the design incorporates a suite of quasi-experimental designs (QEDs) which will enable triangulation between multiple data sources and provide a robust account of the difference the BIP makes to care leavers in Wales. QEDs attempt, in the absence of randomisation, to achieve identification of the causal impact of one or more interventions, primarily through a mix of sample selection and statistical approaches [ 63 ]. Randomisation is not possible in this case because the BIP is open to all eligible young people and starts at the same point for all participants (the month after their 18 th birthday). The QED approach will enable us to determine that, conditional on our sample selection and analytical strategy, we do not expect to see any uncontrolled-for differences between the intervention and counterfactual groups, and so any differences between the two groups can be attributed to the BIP. Further detail about our analysis plan is available in supplementary materials.

We aim to compare the outcomes of care leavers who turn 18 during the enrolment year (and are thereby eligible for the BIP), to outcomes of care leavers in Wales who turn 18 the following year. This will involve two quasi-experimental approaches: coarsened exact Matching (CEM) and difference in differences (DID). Measurement will take place at two time points. Baseline data will be gathered around the individual’s 18 th birthday (referred to below as time t-1) and follow-up data will be gathered around their 20 th birthday (referred to below as time t).

Outcomes and data sources.

The Welsh Government identified six outcome domains of interest, and the literature suggests that it is also important to include physical and mental health outcomes more broadly. These, and the means of collection through surveys and administrative records, described below, are outlined in Table 1 .

https://doi.org/10.1371/journal.pone.0303837.t001

The Welsh Government have not specified what effect they expect BIP to have on these outcomes, though they aim for the policy to empower participants, give them more agency and control, and improve their lives. The literature on basic income suggests that we should not see any detrimental effects in any of these areas, and that in many areas improvements would be hypothesised. Some of these improvements may take longer than others to materialise, meaning that some benefits may not be detectable during the timescale of the study. This study will publish analysis of the observed effects on all outcomes in Table 1 . The measures cited were selected by the evaluation team and approved by the Welsh Government.

Survey data . We are contracted to use data already collected by Coram Voice, who are a third-party commissioned earlier by the funder to gather survey data from participants of the BIP. Surveys will be administered by Coram Voice for the intervention group and comparator group at two time points (t-1; around the participants 18 th birthday, t; around the participants 20 th birthday). It should be noted that both of these time periods differ for each participant in the study, because they turn 18 at different points during the enrolment window. Therefore data collection will, in practice, take place continuously over the study period.

The survey is based on a similar survey used with care leavers extensively in England, called ‘Your Life Beyond Care’ [ 6 ]. Coram Voice started collecting data in Wales in October 2022, 4 months after the pilot had started, and initially included only the original questions used in the ‘Your Life Beyond Care’ survey. In January 2023 an updated survey was released with additional questions designed to cover the broader range of outcomes in Table 1 . The new questions added were the result of negotiations between the evaluation team, the funder, and Coram Voice. At the point we were commissioned, in November 2022, survey response rates for the original survey were 6%. After several changes to the mechanism for collecting survey data were agreed, and questions added, response rates increased and the final response rate is 64%. The Welsh Government and Coram Voice take informed consent for survey data.

Administrative data . We will use the Longitudinal Educational Outcomes (LEO) dataset which is held by the Office for National Statistics (ONS) and the Welsh Government. This resourcelinks educational data from the National Pupil Database (NPD) for England, the Pupil Level Annual School Census (PLASC), the post-16 pupil collection and the Lifelong Learning Wales Record for Wales, employment and earnings data from HM Revenue and Customs (HMRC) and the Department for Work and Pensions (DWP), progression and success in further education from the Individualised Learner Record (DfE) and progression to higher education from the Higher Education Statistics Agency. LEO also contains markers for young people’s social care experience, which will allow us to identify care leavers in both England and Wales. We will initially consider the universe of data on care leavers from England and Wales, and will use a two stage matching process (detailed below and in more detail in our Statistical Analysis Plan), to select a group of English care leavers who are (a) in English local authorities that are comparable to the 22 Welsh local authorities and (b) who are comparable to the Welsh care leavers within those local authorities.

Use of administrative data will allow us to link the intervention group with a large enough comparable group of young people experienced in care during the same period in which the intervention took place. This will provide the analysis with higher power, increasing precision while allowing for a broader range of outcomes to be explored. Administrative data will also allow for a contemporaneous comparison of outcomes between the control and the intervention. This will enhance causal inference with respect to unobserved time-dependent covariates that may have been correlated with the outcome(s) of interest at the time of the intervention, an aspect of analysis which is not possible in the survey-based analysis.

Outcomes within administrative data will be aligned with various outcomes already explored within the survey (see Table 1 ), thus allowing for accurate inference on the effect of the intervention. For outcomes not covered by the survey, a binary interaction indicator of whether the participant was in a local authority that would make them eligible for the basic income payments at the time of the intervention will be used to capture the treatment effect.

Other administrative data will also be available from the Welsh Government. They are managing the enrolment of eligible young people in collaboration with the 22 local authorities. Each participant completes an enrolment form at the outset, and this includes a tick box for consent to be included in the evaluation. Enrolment forms contain a range of monitoring data, including some self-reported data about the individual’s health circumstances. The Welsh Government are designing an exit process that may mirror aspects of enrolment, but are yet to finalise this at the time of writing. Some data items gathered at the enrolment stage for participants in the intervention group will be added to surveys completed by participants in the comparison group (as these data would otherwise be missing for this group). The Welsh Government will take informed consent for monitoring data to be shared with the evaluation team.

Sample size . In the evaluation specification, the Welsh Government advised that around 550 young people were expected to become eligible for the intervention during the enrolment period. (The actual update for the scheme is 635 recipients.) Power calculations are difficult to usefully conduct ex ante for a matched difference-in-differences approach, reflecting the relative complexity compared with the canonical RCT approach. Nonetheless, we anticipate being able to detect effects on survey outcomes of no more than 0.2 standard deviations (calculated via Glass’s Delta), and for effects of no more than 0.12 standard deviations for the administrative data, based on our experience with other similar projects. These effect sizes are comfortably within the range of small effects, allowing us to build a clear picture of the impacts of basic income. However, it should be noted that the small sample size makes subgroup analysis, particularly for any group which is in a minority among eligible participants, difficult to conduct reliably.

Matching procedure . Coarsened Exact Matching (CEM) [ 64 ] lies somewhere between the two extreme forms of matching - the completely uncoarsened Exact Matching, or the logical extreme of coarsening to a single figure - the Propensity Score [ 65 ]. In CEM, matching variables are preserved, but are coarsened. Here, we can think of coarsening as redefining variables into ranges. For example, instead of a participants’ height being an exact number of centimetres, which might be difficult to match in small samples, this could be coarsened to heights in ten centimetres intervals. By doing this, participants continue to be matched on the values of their observable characteristics, but the likelihood of matching on any variable or set of variables is increased.

This matching approach has the advantage of yielding more matches than exact matching, while also ensuring that units are matched on measures that are relevant to the outcomes of interest.

For the administrative data, we will use Coarsened Exact Matching at two levels - first to match Welsh local authorities with their English counterparts, effectively matching treated local authorities to statistically similar untreated authorities, and second to match care leavers within those local authorities with each other. To identify counterfactual local authorities in England we accessed publicly available information on the age, legal basis, gender, and numbers of care leavers in local authorities in England and Wales from 2018-2022, and merged these into a single dataset with a panel at local authority/year level. This panel was then used to identify variables capturing the rate of change in the children in care within each local authority in England and Wales.

We further accessed data on indices of multiple deprivation for England and Wales, particularly focusing on the indices employment, income and childhood deprivation at MSOA level, which was subsequently collapsed to give a local authority level average for each score for all top tier local authorities in England and Wales (which deliver children’s services). This was in turn matched into the panel dataset created previously.

When matching using Income Scores, IDACI score and IDAOPI score, we identified 41 matches for 21 Welsh local authorities. Using Employment Score instead of IDAOPI score produced 29 matches for 18 Welsh Authorities. Reducing this to only Income scores and IDACI Scores yielded 71 matches for all 22 Welsh local authorities. Given the need for some specificity of matches (more than half the local authorities available for matching are matched in the second model) the first or second approach, which only identifies matches for 21/18 Welsh local authorities are preferred at this stage.

For both of our potential models, we test balance on trends in care numbers, and any omitted scores. We find that our second model, which includes Employment rather than IDAOPI, creates a more balanced sample overall, except for with respect to IDAOPI, which is significantly imbalanced.

For survey data, we will match at care leaver level, matching care leavers in the treatment cohort with statistical neighbours in the subsequent cohort (both cohorts being in Wales). Where possible this will involve matching participants on a range of variables including their local authority. Matching for survey data can therefore not take place until after data is collected.

Difference in differences . Difference in Differences approaches are quasi-experimental approaches which compare the differences between treated and counterfactual units, before and after the introduction of a new policy or intervention ( Fig 1 below). This comparison allows for time invariant differences, whether observed or unobserved to be controlled for analytically [ 66 ]. We will undertake two different versions of the difference in difference approach for our two separate data sources. For administrative data, we will make use of a standard difference in difference in which participants in Wales are compared with matched English care leavers, covering the same time period (and same life stage) as the Welsh Data. For our survey outcomes, due to the challenges associated with collecting data from English care leavers, we will instead draw our counterfactual group from the subsequent cohort of Welsh care leavers. Although the comparison of two groups that have not been measured contemporaneously (as is the case comparing Welsh Care leavers in one cohort with Welsh Care leavers in another) is a non-standard implementation of the difference in differences methodology, the underlying assumptions remain the same. Instead of assuming common trends in the macroeconomic conditions (as would be the case for a standard DID), we are instead assuming common trends over the same period of the life course – that is, we assume that outcomes change in the same ways for young people between their 18 th and 20 th birthday, for young people whose 18 th birthdays were up to a year apart. The broad approach to a Difference in Differences approach can be seen in Fig 2 .

https://doi.org/10.1371/journal.pone.0303837.g002

Statistical methods for analysis of impact.

Our analytical strategy for the survey data will follow a matched difference in differences approach. Matching will take place prior to analysis in order to select the most appropriate sample.

The difference in difference strategy for this data will be to take the first time period as baseline survey data for both the treatment and counterfactual groups, and to make use of the endline survey data as the second time period.

Imputation strategy . Inspection of the missing data pattern will provide some initial insight in the type of missingness, and statistical testing will further help assess whether the missing data mechanism is Missing Completely At Random (MCAR) or Missing At Random (MAR). We will utilise Little’s MCAR test [ 68 ], which determines whether the missingness is related to the observed and unobserved data. We will also use a logistic regression model with an indicator of missingness as the outcome, which will show whether relevant covariates are predictive of missingness, pointing towards the plausibility of a MAR assumption.

Due to the nature of survey data collection, we anticipate missing data for some participants. We will not make use of imputation for outcome measures as this carries substantial risks in terms of bias. For missing data at baseline we will make use of a mixture of Multiple Imputation through Chained Equations (MICE) [ 69 ], in which available baseline or demographic data for the participant are used in regression analyses to calculate the likely values of the missing variable. Following imputation of missing data, we will examine the convergence diagnostics to ensure that the imputation process is stable and the imputed values are plausible.

Y ilt is the outcome measure for individual i in local authority l at endline.

α is a regression constant

Y ilt −1 is the lagged value of the participant’s outcome measure at baseline.

B l is a binary indicator of whether the participant was eligible for the basic income payments, set to 1 if they are and 0 else (equivalent to a binary indicator for being in the eligible cohort

X i is a vector of participant level characteristics.

L l is a vector of local authority fixed effects

ϵ lt is an error term clustered at the level of the local authority/time period level.

Follow-up (t) only data . Some variables in the survey are only collected at follow-up (time t), and not at baseline (time t-1). For these variables, we will adopt a less typical approach and replace Y ilt −1 with a vector of baseline variables that are the strongest control group predictors of the outcome at time t.

Y ilt is the outcome measure for individual i in local authority l in time t.

T t is a binary indicator of whether or not the time period in question is that in which the intervention is active.

B l is a binary indicator of whether the participant was in a local authority that would make them eligible for the basic income payments, set to 1 if they are and 0 else (equivalent to a binary indicator for being in Wales).

( T t ∙ B l ) is an interaction term between treatment local authority and treatment time period, which takes values of 1 only for Welsh local authorities during the time period when the intervention is active. This is our treatment variable and its coefficient is our coefficient of interest.

Q l is a vector of local authority level characteristics including those used in matching.

ϵ lt is an error term clustered at the level of the local authority/time period (the level at which the treatment status varies).

Secondary Analysis . Secondary analysis will follow the same regression specification as our primary analysis, but replacing the variable Y with the relevant secondary outcomes.

Robustness Checks . We will robustness check our analyses by:

• Using Null imputation across the board, replacing MICE
• Conducting complete case analysis
• Using logistic and probit regression for binary outcomes

Implementation and process evaluation (IPE)

To understand how and why BIP works, for whom and under which circumstances, we intend to use qualitative and quantitative methods to explore research questions in three main areas of enquiry: (1) implementation, (2) experiences, and (3) integration. This strand of the project will be in dialogue with ongoing theory enhancement, in that questions asked will draw on the initial programme theory, and empirical findings will feed back into ongoing theory enhancement.

Table 2 details the objective and research question attached to each area of interest, and how these are served by the data collection activities specified below. Most qualitative data collection will take place with the same participants early in the pilot intervention and repeated as the pilot draws to a close.

https://doi.org/10.1371/journal.pone.0303837.t002

Data sources for IPE.

The IPE will utilise data from two main sources: quantitative and qualitative monitoring administrative data gathered by the Welsh Government and qualitative data gathered directly from professionals and participants involved in the BIP, and their nominated supporters.

Recruitment to IPE.

Participants of the IPE will be recruited through a range of means. Professionals will be invited via email. Young people who have consented for their contact details to be shared with the evaluation team will be invited by email or phone/ text. Invitations for supporters will be shared with eligible individuals by young people who nominate them, and they will contact the evaluation team if they are interested. Informed consent will be taken from all participants of interviews and focus groups.

Analysis within IPE.

Monitoring data collected during the IPE will be analysed to provide descriptive and inferential statistics on the implementation of the pilot and characteristics of participants. Interview and focus group data will be subject to thematic analysis, a flexible method of identifying, analysing and interpreting patterns of meaning in qualitative data [ 70 ]. Braun and Clarke’s (2006) six-step approach to thematic analysis (familiarisation with the data; generating initial codes; searching for themes; reviewing themes; defining and naming them; producing the report) will provide systematic procedures for generating codes and developing themes. The analysis will be assisted by the use of NVivo software, which will aid management, consideration and visualisation of the data [ 71 ]. In order to generate and refine programme theory we will code qualitative data for key components of the intervention, contexts, mechanisms, and outcomes (CMO’s) in order to delineate how participants perceive the pilot to work. Transcripts from interviews and focus groups, fieldnotes from observations will be read and coded within the NVivo software package. Coded data will then be compared, contrasted and combined, before being represented visually in logic models and described in narrative form. These will be updated during the study as new data becomes available.

Economic evaluation

The economic evaluation will take a public sector and a societal perspective to identify, measure and value the costs and outcomes of BIP, and synthesise the evidence to inform a social cost-benefit analysis. An additional cost-consequences analysis will present costs and consequences in a disaggregated form, together with the estimates of the mean costs of the comparator interventions with appropriate measures of dispersion. They are recommended for complex interventions that may have multiple implications [ 72 ], and for public health interventions which may have an array of benefits that are difficult to synthesise in a common unit such as cost-benefit [ 73 ]. The economic evaluation will be guided by a full economic analysis plan, and will be conducted alongside the impact evaluation, using the same research design and framework.

Data sources for economic data.

Data will be collected from multiple sources and linked, using a mixed methods approach dependent on identified resource-use patterns and the availability of data. The YLBC survey, extended with extra questions for validated measures of well-being and economic impact, will provide baseline data. Throughput and associated costs data will be collected from the client, including use of the St David’s Day Fund and emergency grants. Data will be collected from the comparator cohort to identify baseline funding and other sources of economic engagement. LEO will provide secondary measures extending the cost-consequences analysis to educational and economic engagement, and to other health and social outcomes.

Data items will be captured in disaggregated units where possible, and micro-costing will be performed to capture variance in costing patterns. Unit costs for each resource input will largely be derived from national secondary sources, for example the Department of Health & Social Care’s NHS Reference Costs, the Personal Social Services Resource Unit (PSSRU), Office for National Statistics (ONS). They will be supplemented where necessary using primary research methods. The currency used will be expressed in British Pound Sterling (£), for a base cost year 2024/2025. Adjustments will be made for inflation using the PSSRU hospital & community health services index, and social service resource inputs index. All costs accrued beyond 12 months’ follow-up will be discounted to present values using nationally recommended discount rates [ 74 , 75 ].

Statistical methods for economic analysis.

Specification of comparators and approaches for accounting for selection biases will mirror those planned for the impact evaluation [ 76 , 77 ]. Value for money will initially be expressed in terms of social cost-benefit at 24 months post-intervention, converting outcomes to monetary values. Accepted guidelines outlined in the HM Treasury Green Book [ 78 ] will be followed, constructed to explore the stated objectives of economy, efficiency and effectiveness.

The analysis will be informed by a comprehensive review of the broader literature regarding interventions similar to basic income, and appraisals of that funding approach. The full analysis model will include all cost and outcomes variables, in accordance with the “intention to treat” (ITT) principle. The cost-consequences analysis will make explicit the full range of the intervention’s impacts in disaggregate form. Costs and benefits will be estimated using subjective wellbeing evidence, which aims to capture the direct impact of a policy on wellbeing and broader social impacts such as engagement in education, financial literacy, and psychological well-being. Principles of opportunity cost will underpin all calculations. Missing data from either self-report, linked data or patient surveys will be imputed where appropriate to reduce the impact of missing data on regression results. A range of sensitivity analyses will be conducted to explore the impact of uncertainty surrounding key components of the economic evaluation on economic outcomes. These will be carried out for key costs and outcomes, specifically where they are highly sensitive to certain values or input variables. Sub-group analyses will mirror those undertaken for the main analysis. Summary statistics and cluster analysis may be used to determine data characteristics. Finally, narrative techniques will be used for outcomes which cannot be monetised, or where further exploration will be important, such as financial levers and incentives, mechanisms of change and unintended consequences.

Project management

Data management plans..

As data controller, the Welsh Government have collected data directly from participants with the support of the local authorities. Participants are made aware that the information they provide will be passed on to CASCADE with the option to opt out of this data sharing during enrolment. The evaluation team and Coram Voice are data processors. They receive and have direct access to survey data, as set out in Privacy Notices and information documents.

All data will be stored on Cardiff University servers in restricted folders available only to team members who require access. Data cleaning will be a regular process and data queries will be raised with the Welsh Government and Coram Voice if any discrepancies are found. All data queries will be logged within the tracker, and an audit trail maintained recording any changes to the data. Upon completion of data checks, the data manager will add the data to the master dataset and log the process as complete in the tracker. The following management plans are in place for each type of data.

Survey data . Survey data will be made available to the evaluation team by Coram Voice, via secure data transfer and through the evaluators having access to the ‘Smart survey’ software. Data will be checked, pseudonymised, and prepared for onward sharing to the impact evaluation team at KCL and the economics team at the University of Oxford, who will access databases via the Cardiff University secure server.

Administrative data . Administrative data from the LEO database will be accessed via applications to the Office for National Statistics (English LEO data) and the Welsh Government (Welsh LEO data), and processed within secure environments (e.g. the WISERD education data lab within the social science research park (SPARK) in Cardiff). Administrative data from monitoring forms will be made available to the evaluation team by WG via regular secure data transfers (using Objective Connect). It will be checked and stored on the Cardiff University secure server and deleted at the end of the study in accordance with funder terms and conditions.

Progress will be recorded in a tracking system and all submissions will be quality checked.

Strict data checks will also be completed upon receipt of data collection proformas. The data manager will conduct data cleaning at each time point to ensure there are no missing/duplicated data or any outliers.

Confidentiality and data security

The management plans detailed above will ensure all data is stored securely and processed in accordance with data protection legislation (in accordance with GDPR and UK DPA 18) and Good Clinical Practice (GCP).

Ethical considerations.

The study has ethical approval from the School of Social Sciences Research Ethics Committee of Cardiff University (Ref: SREC/323). Informed consent to participate will be obtained from all participants. Due to the use of remote methods, and in case consent forms are not returned, verbal consent will be audio recorded in interviews with professionals in addition to written consent.

If interviewees say anything that makes the researcher concerned about harm to the participant or another person, then they have a duty to take appropriate action. In the first instance, usually this would involve discussing the concern with the Principal Investigators or a co-investigator. Depending on the nature of the harm, referrals to agencies may be appropriate, for example a referral to the local authority children’s or adults social care services may be deemed necessary if someone was thought to be at risk.

Study status.

The evaluation is underway, following an inception meeting with the Welsh Government on 23rd November 2022. The pilot began several months prior to this, on 1 st July 2022.

This study represents an unprecedented opportunity to understand the impact of a basic income scheme on care leavers, who are a particularly disadvantaged group. The uniqueness of the intervention means that the findings of this evaluation are likely to have a worldwide impact. The evidence it generates about support for care leavers, basic income schemes, and social security more generally is likely to be far reaching. We have designed the study with the limitations of previous basic income pilots in mind. We anticipate being able to provide robust estimates of impact on several key indicators and of value for money, and rich descriptions of the implementation and experiences of those involved.

Nevertheless, there are several challenges. Timing is a particular constraint, since the evaluation was commissioned four months into the 12-month enrolment period. This has two major implications. First, it affects the measurement of baseline outcomes using surveys. Self-report data gathered through surveys is optimal for many of the indicators that a basic income is theorized to affect, such as wellbeing, confidence and mental health indicators, so the Your Life Before Care survey is an important aspect of the evaluation. The survey was designed for (and in collaboration with) care leavers, has been used extensively with this population [ 6 ], and builds on previous work with looked after children [ 79 ]. Yet it was not designed for a basic income pilot, and the unamended survey used until January 2023 did not include some key questions about outcomes of interest. Thus, our baseline data is substantially determined by the content of a survey that was not designed with the evaluation of this pilot in mind.

The second implication of the timing of the evaluation relates to the amount of baseline data available from surveys. While the separate commissioning of Coram Voice to gather survey data at baseline was intended to ameliorate the delay in the evaluation starting, there were also delays in the survey being established, and problems with response rates. The first surveys were completed in October 2022 (3 months after the first participants enrolled), and response rates were unacceptably low (6% in November 2022). Problems with the way surveys were distributed were identified, and processes were consequently simplified and enhanced. This included a ‘thank you’ payment for participants completing the survey, and targeted communication with local authorities, and led to much higher response rates (35% by March 2023; 64% in September 2023 when the baseline intervention group survey was closed). This means some participants will have completed baseline surveys some time after the pilot started, and the data gathered therefore may not reflect the true baseline.

The wide range of outcomes of interest also creates a tension between breadth and brevity. In light of the initial low survey response rates, this has resulted in trade-offs between the extent to which we are able to include a wide range of validated measures and the need for surveys to be accessible and brief for those completing them.

Other challenges have caused us to amend aspects of the study design. We originally intended to run a contemporaneous survey with a matched comparator group of care leavers in England during the enrolment year period. We changed this plan in the first three months after being commissioned to conduct the evaluation. The timing of the start of the evaluation meant that, after allowing for the time period required to have access agreed with gatekeepers in England, the period where surveys in Wales and England could be completed contemporaneously was relatively small. The Welsh Government also favoured a within-Wales comparison for survey data. The change means comparisons for survey and administrative data will differ. We will compare care leavers in Wales in 2022-23 with care leavers in Wales in 2023-24 using survey data, and compare care leavers in Wales in 2022-23 with care leavers in England in 2022-23 using administrative data.

There are limitations and advantages associated with making this pragmatic change. The cohort of Welsh young adults who leave care between July 2023 and June 2024 will experience different labour market conditions due to both the effects of the COVID-19 pandemic and recent increases in the cost of living being experienced in the UK [ 80 ]. The latter in particular makes comparison on some indicators challenging. For example, levels of disposable income and bills may be markedly different for the later cohort if the trends of recent price rises continue. We will account for as much of this contextual variation as possible in in our analysis, but it will affect the confidence we can have in the findings. One advantage of the revised counterfactual plan is that comparator participants will be from the same (i.e. Welsh) local authorities rather than similar (i.e. matched English LAs). The use of triangulation between a range of different data sources, and of multiple analytical approaches, make the study somewhat resilient to these challenges.

Finally, it is important to note that the Welsh Government retain ownership and control of the data. They will publish the findings on their website (see below), and have published guidance that states “There must be no opportunity – or perception of opportunity – for the release of research information (unfavourable or not) to be altered, withheld or delayed for political reasons.” [ 81 ].

Dissemination plans

We are contracted to report the findings in reports that will be published open access by the funder at https://www.gov.wales/statistics-and-research . We will also disseminate the study widely by other means, using in-person and online methods (e.g. conference presentations and invited talks), and by publishing in academic journals.

Acknowledgments

We are grateful to several colleagues who reviewed this paper and offered comments and suggestions. In particular, Carly Jones, Launa Anderson, Gill Davies and Adam Jones offered valuable feedback from a Welsh Government perspective, and Dr. Elliot Johnson provided helpful input from an academic perspective. Members of our strategic advisory group also provided constructive feedback on the initial draft. They are Dr. Belinda Bateman, Professor Heikki Hiilamo, Professor Ive Marx, Dr. Marcia Gibson, Professor Katherine Shelton, Dr. Jose-Luis Fernandez, Tony Wilson, and Dr. Eleanor Ott. We are also pleased to acknowledge colleagues who have worked on the survey design and distribution, in particular Susanna Larsson, Linda Briheim, and Professor Julie Selwyn.

• 1. Jones A.< A basic income to improve population health and well-being in Wales? Cardiff: Public Health Wales NHS Trust, https://phw.nhs.wales/publications/publications1/a-basic-income-to-improve-population-health-and-well-being-in-wales/ (2021, accessed 3 August 2023).
• 2. What is it? – Living Wage Wales, https://livingwage.wales/what-is-it/ (accessed 29 June 2023).
• View Article
• Google Scholar
• 5. Hidden Ambitions. Children’s Commissioner for Wales , https://www.childcomwales.org.uk/publications/hidden-ambitions/ (accessed 7 August 2022).
• 6. Coram Voice, https://coramvoice.org.uk/wp-content/uploads/2020/11/1883-CV-What-Makes-Life-Good-Report-final.pdf (accessed 7 August 2022).
• 7. Pecora P, Kessler R, Williams J, et al. Improving family foster care: Findings from the northwest foster care alumni study .
• 8. Stirling T. Youth homelessness and care leavers : Wales Centre for Public Policy, https://www.wcpp.org.uk/wp-content/uploads/2018/10/Youth-homelessness-and-care-leavers-Mapping-interventions-in-Wales.pdf (2018).
• 13. Episodes finishing for children looked after (aged 16 and over) during the year to 31 March by local authority, gender and reason for finishing, https://statswales.gov.wales/Catalogue/Health-and-Social-Care/Social-Services/Childrens-Services/Children-Looked-After/Care-Leavers-Aged-16-and-Over/episodesfinishingforchildrenlookedafteraged16andoverduringyearto31march-by-localauthority-reasonforfinishing (accessed 7 August 2022).
• 15. Welsh Government. £1 million St David’s Day fund for children who have experienced care. GOV.WALES , https://gov.wales/ps1-million-st-davids-day-fund-children-who-have-experienced-care (2017, accessed 7 August 2022).
• 16. Standing G. Basic income : And how we can make it happen . London: Pelican, 2017.
• 19. Merrill R, Neves C, Laín B. Basic Income Experiments : A Critical Examination of Their Goals , Contexts , and Methods . Cham: Springer International Publishing. Epub ahead of print 2022. https://doi.org/10.1007/978-3-030-89120-6
• 21. Widerquist K. The Vulnerability of Experimental Findings to Misunderstanding, Misuse, Spin, and the Streetlight Effect. In: Widerquist K (ed) A Critical Analysis of Basic Income Experiments for Researchers , Policymakers , and Citizens . Cham: Springer International Publishing, pp. 77–85.
• 22. Stanford Basic Income Lab. Global Map of Basic Income Experiments, https://basicincome.stanford.edu/experiments-map/ (2023, accessed 20 March 2023).
• 24. De Wispelaere J, Halmetoja A, Pulkka V-V. The Finnish Basic Income Experiment: A Primer. In: Torry M (ed) The Palgrave International Handbook of Basic Income . Cham: Springer International Publishing, pp. 389–406.
• 27. California Department of Social Services. Guaranteed Basic Income Projects, https://www.cdss.ca.gov/inforesources/guaranteed-basic-income-projects (accessed 27 March 2023).
• 28. San Francisco Human Services Agency. First State-Funded Guaranteed Income Program, https://www.sfhsa.org/about/announcements/first-state-funded-guaranteed-income-program (2022, accessed 20 March 2023).
• 29. Basic Income Earth Network. Update on the Catalonia UBI pilot, https://basicincome.org/news/2022/12/update-on-the-catalonia-ubi-pilot/ (2022, accessed 20 March 2023).
• 30. Busch J. Basic Income Pilot Project: How does a basic income change our society? We want to know. , https://images.meinbge.de/image/upload/v1/pilot/projektmappe/Basic_Income_Pilot_Project_Magazine.pdf (2020, accessed 20 March 2023).
• 31. Generalitat of Cataloni. Universal Basic Income, http://presidencia.gencat.cat/en/ambits_d_actuacio/renda-basica-universal/index.html (accessed 20 March 2023).
• 33. Hasdell R. What we know about universal basic income : a cross-synthesis of reviews . Basic Income Lab, https://basicincome.stanford.edu/uploads/Umbrella%20Review%20BI_final.pdf (2020, accessed 3 August 2023).
• 34. Basic Income Canada Network. Signposts to Success : Report of a BICN Survey of Ontario Basic Income Recipients . Ontario : Basic Income Canada Network ., https://assets.nationbuilder.com/bicn/pages/42/attachments/original/1551664357/BICN_-_Signposts_to_Success.pdf (2019, accessed 27 March 2023).
• 35. Ferdosi M, McDowell T, Lewchuk W, et al. Southern Ontario’s Basic Income Experience., https://labourstudies.socsci.mcmaster.ca/documents/southern-ontarios-basic-income-experience.pdf (2020, accessed 27 March 2023).
• 37. Marinescu I. No Strings Attached. The Behavioral Effects of U.S. Unconditional Cash Transfer Programs . University of Pennsylvania, https://www.nber.org/system/files/working_papers/w24337/w24337.pdf (2018, accessed 27 March 2023).
• PubMed/NCBI
• 43. The World Bank. BLT Temporary unconditional cash transfer : Social Assistance Program And Public Expenditure Review 2 . Jakarta: The World Bank, https://documents.worldbank.org/pt/publication/documents-reports/documentdetail/652291468039239723/bantuan-langsung-tunai-blt-temporary-unconditional-cash-transfer (2012).
• 45. Optional Freedoms. Boston Review , https://www.bostonreview.net/forum_response/elizabeth-anderson-optional-freedoms/ (accessed 12 April 2023).
• 55. Widerquist K. Overcoming Spin, Sensationalism, Misunderstanding, and the Streetlight Effect. In: Widerquist K (ed) A Critical Analysis of Basic Income Experiments for Researchers , Policymakers , and Citizens . Cham: Springer International Publishing, pp. 145–149.
• 56. Shaw H, Price S. Mapping the potential outcomes of basic income policies and how these might be evaluated . Public Health Wales NHS Trust, https://phw.nhs.wales/services-and-teams/observatory/evidence/evidence-documents/mapping-the-potential-outcomes-of-basic-income-policies-and-how-these-might-be-evaluated/ (2021, accessed 29 June 2023).
• 59. Chen H-T. Theory-driven evaluations . Thousand Oaks, CA, US: Sage Publications, Inc, 1990.
• 60. Pawson R, Tilley N. Realistic evaluation . London: Sage Publications, 1997.
• 61. National Institute for Health and Care Research. UK Standards for Public Involvement , https://sites.google.com/nihr.ac.uk/pi-standards/standards (2019, accessed 27 March 2023).
• 62. Welsh Government. Children and young people’s national participation standards , https://www.gov.wales/children-and-young-peoples-national-participation-standards (6 February 2018, accessed 27 March 2023).
• 63. Shadish WR, Cook TD, Campbell DT. Experimental and quasi-experimental designs for generalized causal inference . Boston, MA, US: Houghton, Mifflin and Company, 2002.
• 66. Mostly Harmless Econometrics | Princeton University Press, https://press.princeton.edu/books/paperback/9780691120355/mostly-harmless-econometrics (2009, accessed 6 March 2024).
• 69. van Buuren S. Flexible Imputation of Missing Data , Second Edition . 2nd ed. New York: Chapman and Hall/CRC, 2018. Epub ahead of print 12 July 2018. https://doi.org/10.1201/9780429492259
• 70. Braun V, Clarke V. Thematic Analysis : A Practical Guide . SAGE, 2021.
• 71. Qualitative Data Analysis with NVivo. Sage Publications Ltd , https://uk.sagepub.com/en-gb/eur/qualitative-data-analysis-with-nvivo/book261349 (2023, accessed 12 April 2023).
• 72. Drummond MF, Sculpher MJ, Torrance GW, et al. Methods for the Economic Evaluation of Health Care Programmes . OUP Catalogue, Oxford University Press, https://econpapers.repec.org/bookchap/oxpobooks/9780198529453.htm (2005, accessed 10 August 2022).
• 74. Introduction to health technology evaluation | NICE health technology evaluations: the manual | Guidance | NICE, https://www.nice.org.uk/process/pmg36/chapter/introduction-to-health-technology-evaluation (accessed 10 August 2022).
• 78. HM Treasury. The Green Book , https://www.gov.uk/government/publications/the-green-book-appraisal-and-evaluation-in-central-governent/the-green-book-2020 (2022, accessed 9 October 2023).
• 81. Welsh Government. Publishing research and analysis in government: GSR Publication Protocol, https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/1078983/2022-GSR_Publication_protocol_v4_Final.pdf (2022, accessed 29 June 2023).