double slit experiment for interference

• Sign in / Register
• Administration
• My Bookmarks
• My Contributions
• Activity Review
• Edit profile

The PhET website does not support your browser. We recommend using the latest version of Chrome, Firefox, Safari, or Edge.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• 13 June 2023
• Correction 20 June 2023

Particle, wave, both or neither? The experiment that challenges all we know about reality

• Anil Ananthaswamy 0

Anil Ananthaswamy is a writer based in California, and author of Through Two Doors at Once .

You can also search for this author in PubMed   Google Scholar

You have full access to this article via your institution.

The double-slit experiment’s interference patterns suggest something is in two places at once. Credit: Huw Jones/Getty

Thomas Young, born 250 years ago this week, was a polymath who made seminal contributions in fields from physics to Egyptology . But perhaps his most enduring legacy is proving Isaac Newton wrong about light — and igniting a debate about the nature of reality that still persists.

“The experiments I am about to relate”, he told the Royal Society of London 1 on 24 November 1803, “may be repeated with great ease, whenever the sun shines.” In a simple, modern form, Young’s ‘double-slit’ experiment involves shining light of a single frequency (say, from a red laser) through two fine, parallel openings in an opaque sheet, onto a screen beyond. If light were made of streams of particles, as Newton conjectured, you would expect to see two distinct strips of light on the screen, where the particles pile up after travelling through one slit or the other. But that’s not what happens. Instead, you see many bands of light and dark, strung out in stripes like a barcode: an interference pattern (see ‘Wave–particle weirdness’).

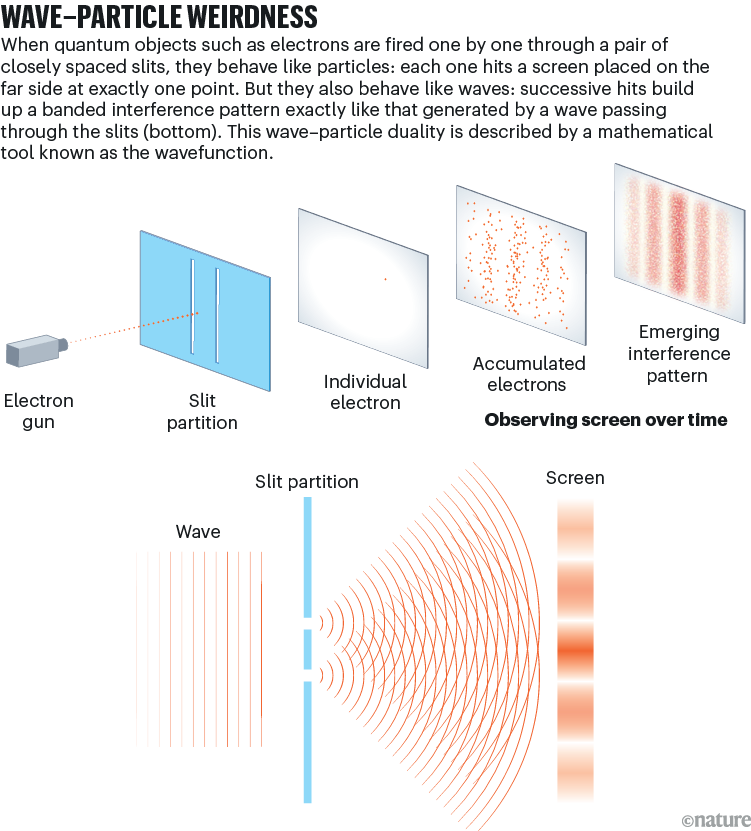
Interference is possible only if light behaves as a wave that strikes both slits at once and diffracts through each, creating two sets of waves on the other side of the slits that propagate towards the screen. Where the crest of one wave overlaps with the crest of the other, you get constructive interference and a patch of light. Where a crest meets a trough, you get destructive interference and darkness.

It’s hard to overstate how wild this discovery was to physicists in Young’s time. But the wildness truly began when Max Planck and Albert Einstein laid the foundations for quantum mechanics in the early twentieth century. Today, quantum mechanics forms a peerlessly accurate framework to explain the basic elements of material reality and their interactions. Pretty early on, it became clear that it implied that light is made of indivisible units of energy called photons — particles, in fact. The amount of energy each carried was proportional to the frequency of the light. Some carry enough of a wallop to knock electrons off atoms of metal, giving us the photoelectric effect that enables today’s solar cells. (It was the study of this effect that led Einstein to his conclusions about light’s particulate nature.)

With the emergence of quantum mechanics, the idea of light as a wave faced a challenge. But it wasn’t as simple as going back to the particle view. Further tests of quantum theory using the double-slit experiment only deepened the mystery. And it hasn’t been solved yet.

Singularly quantum

Imagine, now, that your light source can shoot individual photons of red light at the two slits, while guaranteeing that only one photon goes through the apparatus at any time. A photographic plate on the other side records where the photons land. Classical intuition says each photon can go through only one slit or the other. So, this time, we should see photons accumulating over time and forming two strips of light on the photographic plate. Yet the mathematics of quantum theory implied that the interference pattern would persist.

It was several decades before the technology matured enough to verify these predictions experimentally, using more complex set-ups that were in principle the double-slit. At first, it wasn’t done with photons, but with electrons — entities that we know as particles, but that quantum mechanics predicts act as waves, too. Then, in the 1980s, a team led by Alain Aspect at the Optical Institute in Palaiseau, France, performed the double-slit experiment with single photons 2 . Quantum theory won out: an interference pattern emerged, even when only single particles passed through the slits.

‘Spooky’ quantum-entanglement experiments win physics Nobel

Aspect won a share of the 2022 Nobel prize in physics for his contribution to confirming the predictions of quantum mechanics through experiment. But such experiments leave matters of interpretation wide open. There is simply no way to comprehend what’s happening with minds attuned to the classical world of everyday objects.

When it comes to the double-slit experiment, quantum mechanics does tell a form of story. It says that a photon’s position is described by a mathematical abstraction called the wavefunction — which, as the name suggests, behaves like a wave. This wavefunction, mathematically speaking, hits the two slits, diffracts into two sets of waves and recombines to create the interference pattern. The value of the wavefunction at any location on the photographic plate lets you calculate the probability of finding the photon there. The probability is very high in regions of constructive interference, and very low in regions of destructive interference.

In a sense, then, a photon or any other quantum object acts like both a particle and a wave. This ‘wave–particle duality’ embodies many of the central conceptual mysteries of quantum mechanics that are unresolved to this day. Even if you could know everything about a photon’s initial state, there’s no way to tell exactly where it’ll land on the detector. You have to talk in terms of probabilities given by the wavefunction. These probabilities are borne out only when thousands or tens of thousands of photons are sent through the double slit, one by one.

Before the measurement — in this case, detection by the photographic plate — the mathematics says the particle exists in a superposition of states: in a sense, it has taken both paths, through the right slit and the left. Standard quantum mechanics says that the wavefunction ‘collapses’ when measured, and that the act of observation in some way precipitates that collapse. Before this, the photon has a finite probability of being found in many different regions, but on measurement, the wavefunction peaks at the location in which the photon appears (the probability there equals 1) and is nullified everywhere else (probability equals 0).

It gets even odder. If you can determine which path the photon took on its way to the detector, it acts like a particle that does indeed go through one slit or the other: the interference pattern disappears. But if you cannot glean this ‘which-way’ information, the photon acts like a wave. Whenever there are two or more ways for a photon — or, indeed, any quantum object — to get to a final state, quantum interference occurs.

What’s a wavefunction?

But to generate interference, something has to go through — or at least interact in some way with — both slits. In the mathematics, the wavefunction does the job. Some physicists would say that the wavefunction simply represents information about the quantum system and is not real — in which case it’s hard to explain what interacts with both slits at once. But you can explain the interference pattern if you consider the wavefunction to be real.

This creates its own problems. Imagine a real wavefunction that spreads for kilometres and kilometres before an observer detects the photon. At this point, the wavefunction peaks at the photon’s location, and simultaneously drops to zero everywhere else — over a large, macroscopic distance. This suggests a kind of instantaneous, non-local influence that bothered Einstein no end. One can avoid this with interpretations of quantum theory that don’t collapse the wavefunction, but that opens other cans of worms.

Thomas Young reported the results of the original double-slit experiment in the early nineteenth century. Credit: Photo Researchers/SPL

Perhaps the most notorious is the many-worlds interpretation, the brainchild of US physicist Hugh Everett in the 1950s. This argues that every possible event — in the case of the double slit, a particle going through the left and the right slit — happens, each in its own world. There is no collapse: measurement simply reveals the state of the quantum system in that world. Detractors ask how it’s possible to justify this constant proliferation of worlds, and how, in a many-worlds framework, you can explain why measuring quantum systems yields probabilities, given that there are always definite outcomes in each world.

The de Broglie–Bohm theory, named after quantum pioneers Louis de Broglie and David Bohm, provides another alternative. It says that particles exist with definite positions and momenta, but are guided by an all-encompassing, invisible ‘pilot’ wave, and it’s this wave that goes through both slits. The most profound implication of this theory, that everything is linked to everything else in the Universe by the underlying pilot wave, is one many physicists have trouble accepting.

In the 1970s and 1980s, physicists upgraded the double-slit experiment to seek clarity about the nature of quantum reality, and the perplexing role observation apparently has in collapsing a defined, classical reality out of it. Most notably, John Wheeler at the University of Texas at Austin designed the ‘delayed choice’ thought experiment 3 . Imagine a double-slit set-up that gives the option of gathering or ignoring information about which way the particle went. If you ignore the ‘which-way’ information, you get wave-like behaviour; if you don’t, you get particle-like patterns.

Superconducting qubits cover new distances

With the apparatus on the ‘collect which-way information’ setting, send a photon through the double slits. It should act like a particle and go through one slit or the other. But just before the photon lands on the detector, flip the apparatus to ignore the which-way information. Will the photon, until then supposedly a particle, suddenly switch to being a wave?

Decades later, Aspect’s team performed this experiment with single photons and showed that the answer is yes 4 . Even if the photon had ostensibly travelled through the entire set-up as a particle, switching the apparatus setting so that it ignored which-way information caused it to act like a wave. Did the photon travel back in time and come back through the two slits as a wave? To avoid such nonsensical explanations, Wheeler argued that the only way to make sense of the experiment was to say that the photon has no reality — it’s neither wave nor particle — until it’s detected.

Back in the 1980s, Marlan Scully, then at the University of New Mexico in Albuquerque, and his colleagues came up with a similarly befuddling thought experiment 5 . They imagined collecting the which-way information about a photon by using a second photon ‘entangled’ with the first — a situation in which measuring the quantum state of one tells you about the quantum state of the other. As long as the which-way information can in principle be extracted, the first photon should act like a particle. But if you erase the information in the entangled partner, the mathematics showed, the first photon goes back to behaving like a wave. In 2000, Scully, Yoon-Ho Kim and their colleagues reported performing this experiment 6 . Surprisingly — or unsurprisingly, by this stage — intuition was once again defeated and quantum weirdness reigned supreme.

Larger and still larger

Others are still pushing the double slit in new directions. This year, Romain Tirole at Imperial College London and his colleagues described an experiment in which the slits were temporal: one slit was open at one point in time and the second slit an instant later 7 . A beam of light that goes through these temporal slits produces an interference pattern in its frequency spectrum. Again, the mathematics predicts exactly this behaviour, so physicists aren’t surprised. But it is more proof that the double-slit experiment highlights the lacunae in our understanding of reality, a quarter of a millennium after the birth of the man who devised it.

The double-slit experiment’s place in the pantheon of physics experiments is assured. But it would be further cemented if and when physicists using it were able to work out which theory of the quantum world is correct.

For example, some theories posit that quantum systems that grow bigger than a certain, as-yet-undetermined size randomly collapse into classical systems, with no observer needed. This would explain why macroscopic objects around us don’t obviously work according to quantum rules — but how big does something have to be before it stops acting in a quantum way?

In 2019, Markus Arndt and Yaakov Fein at the University of Vienna and their colleagues reported sending macromolecules called oligoporphyrins, composed of up to 2,000 atoms, through a double slit to see whether they produce an interference pattern 8 . They do, and these patterns can be explained only as a quantum phenomenon. Arndt’s team and others continue to push such experiments to determine whether a line exists between the quantum and the classical world.

Last year, Siddhant Das at the Ludwig Maximilian University of Munich, Germany, and his colleagues analysed the double-slit experiment in the context of the de Broglie–Bohm theory 9 . Unlike standard quantum mechanics, this predicts not just the distribution of particles on the screen that leads to the spatial interference pattern, but also the distribution of when the particles arrive at the screen. The researchers found that their calculations on the distribution of arrival times agreed qualitatively with observations made two decades before, in a double-slit experiment using helium atoms 10 . But it was difficult to prove their case definitively. They are awaiting better data from a similar double-slit experiment done with current technology, to see whether it matches predictions.

And so it goes on, a world away from anything Young or his peers at the Royal Society could have conceived of more than two centuries ago. “Thomas Young would probably scratch his head if he could see the status of today’s experiments,” says Arndt. But that’s because his experiment, so simple in concept, has left us scratching our heads to this day.

Nature 618 , 454-456 (2023)

doi: https://doi.org/10.1038/d41586-023-01938-6

Updates & Corrections

Correction 20 June 2023 : An earlier version of the second picture caption gave the wrong date for when Young reported results of a double-slit experiment.

Young, T. Phil. Trans. R. Soc. 94 , 1–16 (1804).

Google Scholar  

Grangier, P., Roger, G. & Aspect, A. Europhys. Lett. 1 , 173 (1986).

Article   Google Scholar  

Miller, W. A. & Wheeler, J. A. Foundations of Quantum Mechanics in the Light of New Technology (Eds Nakajima, S., Murayama, Y. & Tonomura, A.) 72–84 (World Scientific, 1997).

Jacques, V. et al. Science 315 , 966–968 (2007).

Article   PubMed   Google Scholar  

Scully, M. O. & Drühl, K. Phys. Rev. A. 25 , 2208 (1982).

Kim, Y.-H. et al. Phys. Rev. Lett. 84 , 1 (2000).

Tirole, R. et al. Nature Phys . https://doi.org/10.1038/s41567-023-01993-w (2023).

Fein, Y. Y. et al. Nature Phys. 15 , 1242–1245 (2019).

Das, S., Deckert, D.-A., Kellers, L. & Struyve, W. Preprint at https://arxiv.org/abs/2211.13362 (2022).

Kurtsiefer, Ch., Pfau T. & Mlynek, J. Nature 386 , 150–153 (1997).

Download references

Competing Interests

The author declares no competing interests.

Related Articles

• Quantum physics
• Quantum information

Thirty years since the race to the BRCA1 gene

News & Views 30 OCT 24

Civil engineer Herbert Stone’s rock-solid views on Stonehenge

News & Views 29 OCT 24

Splendid squirrel sneezes at will

News & Views 22 OCT 24

Physicists tame fundamental muon particles into highly controlled beam for first time

News 24 OCT 24

Consider the ethical impacts of quantum technologies in defence — before it’s too late

Comment 22 OCT 24

Multi-qubit gates and Schrödinger cat states in an optical clock

Article 09 OCT 24

Universal quantum operations and ancilla-based read-out for tweezer clocks

Phase transitions in random circuit sampling

PhD studentship in Analytical Chemistry

Urban Lab invites applications for PhD studentship in Analytical Chemistry. The graduate research will encompass development of novel analytical to...

Hsinchu (TW)

Urban Lab at National Tsing Hua University

Global Faculty Recruitment of School of Life Sciences, Tsinghua University

The School of Life Sciences at Tsinghua University invites applications for tenure-track or tenured faculty positions at all ranks (Assistant/Ass...

Beijing, China

Tsinghua University (The School of Life Sciences)

Full-Time Faculty Member in Molecular Agrobiology at Peking University

Faculty positions in molecular agrobiology, including plant (crop) molecular biology, crop genomics and agrobiotechnology and etc.

School of Advanced Agricultural Sciences, Peking University

Tenure-track Faculty Positions in Particle Physics and Cosmology

Faculty Positions in Particle Physics and Cosmology

Hong Kong (HK)

Department of Physics, The Hong Kong University of Science & Technology (HKUST)

Assistant/Associate Professor

Center for Virology and Vaccine Research at Beth Israel Deaconess Medical Center is seeking Assistant or Associate Professor.

Boston, Massachusetts (US)

Beth Israel Deaconess Medical Center (BIDMC)

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

27.3 Young’s Double Slit Experiment

Learning objectives.

By the end of this section, you will be able to:

• Explain the phenomena of interference.
• Define constructive interference for a double slit and destructive interference for a double slit.

Although Christiaan Huygens thought that light was a wave, Isaac Newton did not. Newton felt that there were other explanations for color, and for the interference and diffraction effects that were observable at the time. Owing to Newton’s tremendous stature, his view generally prevailed. The fact that Huygens’s principle worked was not considered evidence that was direct enough to prove that light is a wave. The acceptance of the wave character of light came many years later when, in 1801, the English physicist and physician Thomas Young (1773–1829) did his now-classic double slit experiment (see Figure 27.10 ).

Why do we not ordinarily observe wave behavior for light, such as observed in Young’s double slit experiment? First, light must interact with something small, such as the closely spaced slits used by Young, to show pronounced wave effects. Furthermore, Young first passed light from a single source (the Sun) through a single slit to make the light somewhat coherent. By coherent , we mean waves are in phase or have a definite phase relationship. Incoherent means the waves have random phase relationships. Why did Young then pass the light through a double slit? The answer to this question is that two slits provide two coherent light sources that then interfere constructively or destructively. Young used sunlight, where each wavelength forms its own pattern, making the effect more difficult to see. We illustrate the double slit experiment with monochromatic (single λ λ ) light to clarify the effect. Figure 27.11 shows the pure constructive and destructive interference of two waves having the same wavelength and amplitude.

When light passes through narrow slits, it is diffracted into semicircular waves, as shown in Figure 27.12 (a). Pure constructive interference occurs where the waves are crest to crest or trough to trough. Pure destructive interference occurs where they are crest to trough. The light must fall on a screen and be scattered into our eyes for us to see the pattern. An analogous pattern for water waves is shown in Figure 27.12 (b). Note that regions of constructive and destructive interference move out from the slits at well-defined angles to the original beam. These angles depend on wavelength and the distance between the slits, as we shall see below.

To understand the double slit interference pattern, we consider how two waves travel from the slits to the screen, as illustrated in Figure 27.13 . Each slit is a different distance from a given point on the screen. Thus different numbers of wavelengths fit into each path. Waves start out from the slits in phase (crest to crest), but they may end up out of phase (crest to trough) at the screen if the paths differ in length by half a wavelength, interfering destructively as shown in Figure 27.13 (a). If the paths differ by a whole wavelength, then the waves arrive in phase (crest to crest) at the screen, interfering constructively as shown in Figure 27.13 (b). More generally, if the paths taken by the two waves differ by any half-integral number of wavelengths [ ( 1 / 2 ) λ ( 1 / 2 ) λ , ( 3 / 2 ) λ ( 3 / 2 ) λ , ( 5 / 2 ) λ ( 5 / 2 ) λ , etc.], then destructive interference occurs. Similarly, if the paths taken by the two waves differ by any integral number of wavelengths ( λ λ , 2 λ 2 λ , 3 λ 3 λ , etc.), then constructive interference occurs.

Take-Home Experiment: Using Fingers as Slits

Look at a light, such as a street lamp or incandescent bulb, through the narrow gap between two fingers held close together. What type of pattern do you see? How does it change when you allow the fingers to move a little farther apart? Is it more distinct for a monochromatic source, such as the yellow light from a sodium vapor lamp, than for an incandescent bulb?

Figure 27.14 shows how to determine the path length difference for waves traveling from two slits to a common point on a screen. If the screen is a large distance away compared with the distance between the slits, then the angle θ θ between the path and a line from the slits to the screen (see the figure) is nearly the same for each path. The difference between the paths is shown in the figure; simple trigonometry shows it to be d sin θ d sin θ , where d d is the distance between the slits. To obtain constructive interference for a double slit , the path length difference must be an integral multiple of the wavelength, or

Similarly, to obtain destructive interference for a double slit , the path length difference must be a half-integral multiple of the wavelength, or

where λ λ is the wavelength of the light, d d is the distance between slits, and θ θ is the angle from the original direction of the beam as discussed above. We call m m the order of the interference. For example, m = 4 m = 4 is fourth-order interference.

The equations for double slit interference imply that a series of bright and dark lines are formed. For vertical slits, the light spreads out horizontally on either side of the incident beam into a pattern called interference fringes, illustrated in Figure 27.15 . The intensity of the bright fringes falls off on either side, being brightest at the center. The closer the slits are, the more is the spreading of the bright fringes. We can see this by examining the equation

For fixed λ λ and m m , the smaller d d is, the larger θ θ must be, since sin θ = mλ / d sin θ = mλ / d . This is consistent with our contention that wave effects are most noticeable when the object the wave encounters (here, slits a distance d d apart) is small. Small d d gives large θ θ , hence a large effect.

Example 27.1

Finding a wavelength from an interference pattern.

Suppose you pass light from a He-Ne laser through two slits separated by 0.0100 mm and find that the third bright line on a screen is formed at an angle of 10 . 95º 10 . 95º relative to the incident beam. What is the wavelength of the light?

The third bright line is due to third-order constructive interference, which means that m = 3 m = 3 . We are given d = 0 . 0100 mm d = 0 . 0100 mm and θ = 10 . 95º θ = 10 . 95º . The wavelength can thus be found using the equation d sin θ = mλ d sin θ = mλ for constructive interference.

The equation is d sin θ = mλ d sin θ = mλ . Solving for the wavelength λ λ gives

Substituting known values yields

To three digits, this is the wavelength of light emitted by the common He-Ne laser. Not by coincidence, this red color is similar to that emitted by neon lights. More important, however, is the fact that interference patterns can be used to measure wavelength. Young did this for visible wavelengths. This analytical technique is still widely used to measure electromagnetic spectra. For a given order, the angle for constructive interference increases with λ λ , so that spectra (measurements of intensity versus wavelength) can be obtained.

Example 27.2

Calculating highest order possible.

Interference patterns do not have an infinite number of lines, since there is a limit to how big m m can be. What is the highest-order constructive interference possible with the system described in the preceding example?

Strategy and Concept

The equation d sin θ = mλ (for m = 0, 1, − 1, 2, − 2, … ) d sin θ = mλ (for m = 0, 1, − 1, 2, − 2, … ) describes constructive interference. For fixed values of d d and λ λ , the larger m m is, the larger sin θ sin θ is. However, the maximum value that sin θ sin θ can have is 1, for an angle of 90º 90º . (Larger angles imply that light goes backward and does not reach the screen at all.) Let us find which m m corresponds to this maximum diffraction angle.

Solving the equation d sin θ = mλ d sin θ = mλ  for  m m gives

Taking sin θ = 1 sin θ = 1 and substituting the values of d d and λ λ from the preceding example gives

Therefore, the largest integer m m can be is 15, or

The number of fringes depends on the wavelength and slit separation. The number of fringes will be very large for large slit separations. However, if the slit separation becomes much greater than the wavelength, the intensity of the interference pattern changes so that the screen has two bright lines cast by the slits, as expected when light behaves like a ray. We also note that the fringes get fainter further away from the center. Consequently, not all 15 fringes may be observable.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/27-3-youngs-double-slit-experiment

© Jul 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Reset password New user? Sign up

Existing user? Log in

Double-slit Experiment

Already have an account? Log in here.

Plane wave representing a particle passing through two slits, resulting in an interference pattern on a screen some distance away from the slits. [1] .

The double-slit experiment is an experiment in quantum mechanics and optics demonstrating the wave-particle duality of electrons , photons , and other fundamental objects in physics. When streams of particles such as electrons or photons pass through two narrow adjacent slits to hit a detector screen on the other side, they don't form clusters based on whether they passed through one slit or the other. Instead, they interfere: simultaneously passing through both slits, and producing a pattern of interference bands on the screen. This phenomenon occurs even if the particles are fired one at a time, showing that the particles demonstrate some wave behavior by interfering with themselves as if they were a wave passing through both slits.

Niels Bohr proposed the idea of wave-particle duality to explain the results of the double-slit experiment. The idea is that all fundamental particles behave in some ways like waves and in other ways like particles, depending on what properties are being observed. These insights led to the development of quantum mechanics and quantum field theory , the current basis behind the Standard Model of particle physics , which is our most accurate understanding of how particles work.

The original double-slit experiment was performed using light/photons around the turn of the nineteenth century by Thomas Young, so the original experiment is often called Young's double-slit experiment. The idea of using particles other than photons in the experiment did not come until after the ideas of de Broglie and the advent of quantum mechanics, when it was proposed that fundamental particles might also behave as waves with characteristic wavelengths depending on their momenta. The single-electron version of the experiment was in fact not performed until 1974. A more recent version of the experiment successfully demonstrating wave-particle duality used buckminsterfullerene or buckyballs , the \(C_{60}\) allotrope of carbon.

Waves vs. Particles

Double-slit experiment with electrons, modeling the double-slit experiment.

To understand why the double-slit experiment is important, it is useful to understand the strong distinctions between wave and particles that make wave-particle duality so intriguing.

Waves describe oscillating values of a physical quantity that obey the wave equation . They are usually described by sums of sine and cosine functions, since any periodic (oscillating) function may be decomposed into a Fourier series . When two waves pass through each other, the resulting wave is the sum of the two original waves. This is called a superposition since the waves are placed ("-position") on top of each other ("super-"). Superposition is one of the most fundamental principles of quantum mechanics. A general quantum system need not be in one state or another but can reside in a superposition of two where there is some probability of measuring the quantum wavefunction in one state or another.

Left: example of superposed waves constructively interfering. Right: superposed waves destructively interfering. [2]

If one wave is \(A(x) = \sin (2x)\) and the other is \(B(x) = \sin (2x)\), then they add together to make \(A + B = 2 \sin (2x)\). The addition of two waves to form a wave of larger amplitude is in general known as constructive interference since the interference results in a larger wave.

If one wave is \(A(x) = \sin (2x)\) and the other is \(B(x) = \sin (2x + \pi)\), then they add together to make \(A + B = 0\) \(\big(\)since \(\sin (2x + \pi) = - \sin (2x)\big).\) This is known as destructive interference in general, when adding two waves results in a wave of smaller amplitude. See the figure above for examples of both constructive and destructive interference.

Two speakers are generating sounds with the same phase, amplitude, and wavelength. The two sound waves can make constructive interference, as above left. Or they can make destructive interference, as above right. If we want to find out the exact position where the two sounds make destructive interference, which of the following do we need to know?

a) the wavelength of the sound waves b) the distances from the two speakers c) the speed of sound generated by the two speakers

This wave behavior is quite unlike the behavior of particles. Classically, particles are objects with a single definite position and a single definite momentum. Particles do not make interference patterns with other particles in detectors whether or not they pass through slits. They only interact by colliding elastically , i.e., via electromagnetic forces at short distances. Before the discovery of quantum mechanics, it was assumed that waves and particles were two distinct models for objects, and that any real physical thing could only be described as a particle or as a wave, but not both.

In the more modern version of the double slit experiment using electrons, electrons with the same momentum are shot from an "electron gun" like the ones inside CRT televisions towards a screen with two slits in it. After each electron goes through one of the slits, it is observed hitting a single point on a detecting screen at an apparently random location. As more and more electrons pass through, one at a time, they form an overall pattern of light and dark interference bands. If each electron was truly just a point particle, then there would only be two clusters of observations: one for the electrons passing through the left slit, and one for the right. However, if electrons are made of waves, they interfere with themselves and pass through both slits simultaneously. Indeed, this is what is observed when the double-slit experiment is performed using electrons. It must therefore be true that the electron is interfering with itself since each electron was only sent through one at a time—there were no other electrons to interfere with it!

When the double-slit experiment is performed using electrons instead of photons, the relevant wavelength is the de Broglie wavelength \(\lambda:\)

\[\lambda = \frac{h}{p},\]

where \(h\) is Planck's constant and \(p\) is the electron's momentum.

Calculate the de Broglie wavelength of an electron moving with velocity \(1.0 \times 10^{7} \text{ m/s}.\)

Usain Bolt, the world champion sprinter, hit a top speed of 27.79 miles per hour at the Olympics. If he has a mass of 94 kg, what was his de Broglie wavelength?

Express your answer as an order of magnitude in units of the Bohr radius \(r_{B} = 5.29 \times 10^{-11} \text{m}\). For instance, if your answer was \(4 \times 10^{-5} r_{B}\), your should give \(-5.\)

Image Credit: Flickr drcliffordchoi.

While the de Broglie relation was postulated for massive matter, the equation applies equally well to light. Given light of a certain wavelength, the momentum and energy of that light can be found using de Broglie's formula. This generalizes the naive formula \(p = m v\), which can't be applied to light since light has no mass and always moves at a constant velocity of \(c\) regardless of wavelength.

The below is reproduced from the Amplitude, Frequency, Wave Number, Phase Shift wiki.

In Young's double-slit experiment, photons corresponding to light of wavelength \(\lambda\) are fired at a barrier with two thin slits separated by a distance \(d,\) as shown in the diagram below. After passing through the slits, they hit a screen at a distance of \(D\) away with \(D \gg d,\) and the point of impact is measured. Remarkably, both the experiment and theory of quantum mechanics predict that the number of photons measured at each point along the screen follows a complicated series of peaks and troughs called an interference pattern as below. The photons must exhibit the wave behavior of a relative phase shift somehow to be responsible for this phenomenon. Below, the condition for which maxima of the interference pattern occur on the screen is derived.

Left: actual experimental two-slit interference pattern of photons, exhibiting many small peaks and troughs. Right: schematic diagram of the experiment as described above. [3]

Since \(D \gg d\), the angle from each of the slits is approximately the same and equal to \(\theta\). If \(y\) is the vertical displacement to an interference peak from the midpoint between the slits, it is therefore true that

\[D\tan \theta \approx D\sin \theta \approx D\theta = y.\]

Furthermore, there is a path difference \(\Delta L\) between the two slits and the interference peak. Light from the lower slit must travel \(\Delta L\) further to reach any particular spot on the screen, as in the diagram below:

Light from the lower slit must travel further to reach the screen at any given point above the midpoint, causing the interference pattern.

The condition for constructive interference is that the path difference \(\Delta L\) is exactly equal to an integer number of wavelengths. The phase shift of light traveling over an integer \(n\) number of wavelengths is exactly \(2\pi n\), which is the same as no phase shift and therefore constructive interference. From the above diagram and basic trigonometry, one can write

\[\Delta L = d\sin \theta \approx d\theta = n\lambda.\]

The first equality is always true; the second is the condition for constructive interference.

Now using \(\theta = \frac{y}{D}\), one can see that the condition for maxima of the interference pattern, corresponding to constructive interference, is

\[n\lambda = \frac{dy}{D},\]

i.e. the maxima occur at the vertical displacements of

\[y = \frac{n\lambda D}{d}.\]

The analogous experimental setup and mathematical modeling using electrons instead of photons is identical except that the de Broglie wavelength of the electrons \(\lambda = \frac{h}{p}\) is used instead of the literal wavelength of light.

• Lookang, . CC-3.0 Licensing . Retrieved from https://commons.wikimedia.org/w/index.php?curid=17014507
• Haade, . CC-3.0 Licensing . Retrieved from https://commons.wikimedia.org/w/index.php?curid=10073387
• Jordgette, . CC-3.0 Licensing . Retrieved from https://commons.wikimedia.org/w/index.php?curid=9529698

Problem Loading...

Note Loading...

Set Loading...