quantitative research large sample size

Translation

The importance of having Large Sample Sizes for your research

By charlesworth author services.

Charlesworth Author Services
26 May, 2022

Sample size can be defined as the number of pieces of information, data points or patients (in medical studies) tested or enrolled in an experiment or study . On any hypothesis , scientific research is built upon determining the mean values of a given dataset. The larger the sample size, the more accurate the average values will be. Larger sample sizes also help researchers identify outliers in data and provide smaller margins of error.

But just what is a ‘large scientific study’ with a ‘large sample size’?

Why are such studies important?

What type of research benefits most from large sample sizes?

And how can a researcher ensure they have an adequately large study?

Here, we discuss these various aspects of studies with large sample sizes.

Defining ‘large sample size’ / ‘large study’ by topic

The size of a ‘large’ study depends on the topic.

In medicine , large studies investigating common conditions such as heart disease or cancer may enrol tens of thousands of patients with multiple years of follow-up.
For specialty journals , ‘large studies’ may include clinical studies with hundreds of patients.
For highly specialised topics (such as certain rare genetic conditions), large patient populations may not exist. For such research, a ‘large’ study may enrol the entire known global population with the condition, which could be as few as dozens of patients.

Statistical importance of having a large sample size

Larger studies provide stronger and more reliable results because they have smaller margins of error and lower standards of deviation . (Standard deviation measures how spread out the data values are from the mean. The larger the study sample size, the smaller the margin of error.)
Larger sample sizes allow researchers to control the risk of reporting false-negative or false-positive findings . The greater number of samples, the greater the precision of results will be.

A useful primer that discusses the importance of sample size in planning and interpreting medical research can be found here .

Fields that benefit most from large sample sizes

Large sample sizes benefit many fields of research, including:

Medicine : Quality efficacy of treatment protocols, anatomic studies and biomechanical investigations all require large sample sizes. Ongoing COVID-19 vaccine trials depend on large volunteer patient populations.
Natural sciences : Long-term climate studies, agricultural science, zoology and the like all require large studies with thousands of data points.
Social sciences : Much social science research, public opinion and political polls, census and other demographic information, etc. rely heavily on large-scale survey studies.

Importance of a larger sample size from a publishing perspective

Academic publishers seek to publish research with the highest-quality, most-reliable and most-certain data. As an author, it is greatly to your advantage to submit manuscripts based on studies having as large a sample size as possible.

That said, there are limits to certainty and reliability of results. But that discussion would be beyond the scope of this article.

Determining an adequate sample size

In determining an adequate sample size for an experiment, you must establish the following:

Justifiable level of statistical significance
Chances of detecting a difference of given magnitude between the groups compared (the study’s power)
Targeted difference (effect size)
Variability of the data

Ensuring you have an adequately large study

Working with a biostatistician and experts familiar with study design will help you determine how large a study sample you need in order to determine a highly accurate answer to your specific hypothesis.

Note that not all research questions require massively large sample sizes. However, many do, and for such research, you may need to design, obtain funding for and conduct a multi-centre study or meta-analysis of existing studies .

Note : Multi-centre studies may come with many logistical, financial, ethical and analytical challenges. But when properly designed and executed, they provide some of the most definitive and highly cited publications.

One of the main goals of scientific research and publishing is to answer questions with as much certainty as possible. Ensuring large sample sizes in research studies would go a long way towards providing sufficient levels of certitude. Such large studies benefit numerous research applications in a wide variety of scientific and social science fields.

Maximise your publication success with Charlesworth Author Services.

Charlesworth Author Services, a trusted brand supporting the world’s leading academic publishers, institutions and authors since 1928.

To know more about our services, visit: Our Services

Share with your colleagues

Scientific Editing Services

We use cookies to offer you a personalized experience. By continuing to use this website, you consent to the use of cookies in accordance with our Cookie Policy.

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

Publications
Account settings
Advanced Search
Journal List

When is enough, enough? Understanding and solving your sample size problems in health services research

Victoria pye, natalie taylor, robyn clay-williams, jeffrey braithwaite.

Author information
Article notes
Copyright and License information

Corresponding author.

Received 2016 Jan 15; Accepted 2016 Jan 28; Collection date 2016.

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated.

Health services researchers face two obstacles to sample size calculation: inaccessible, highly specialised or overly technical literature, and difficulty securing methodologists during the planning stages of research. The purpose of this article is to provide pragmatic sample size calculation guidance for researchers who are designing a health services study. We aimed to create a simplified and generalizable process for sample size calculation, by (1) summarising key factors and considerations in determining a sample size, (2) developing practical steps for researchers—illustrated by a case study and, (3) providing a list of resources to steer researchers to the next stage of their calculations. Health services researchers can use this guidance to improve their understanding of sample size calculation, and implement these steps in their research practice.

Electronic supplementary material

The online version of this article (doi:10.1186/s13104-016-1893-x) contains supplementary material, which is available to authorized users.

Keywords: Sample size, Effect size, Health services research, Methodologies

Sample size literature for randomized controlled trials and study designs in which there is a clear hypothesis, single outcome measure, and simple comparison groups is available in abundance. Unfortunately health services research does not always fit into these constraints. Rather, it is often cross-sectional, and observational (i.e., with no ‘experimental group’) with multiple outcomes measured simultaneously. It can also be difficult work with no a priori hypothesis. The aim of this paper is to guide researchers during the planning stages to adequately power their study and to avoid the situation described in Fig. 1 . By blending key pieces of methodological literature with a pragmatic approach, researchers will be equipped with valuable information to plan and conduct sufficiently powered research using appropriate methodological designs. A short case study is provided (Additional file 1 ) to illustrate how these methods can be applied in practice.

A statistician’s dilemma

The importance of an accurate sample size calculation when designing quantitative research is well documented [ 1 – 3 ]. Without a carefully considered calculation, results can be missed, biased or just plain incorrect. In addition to squandering precious research funds, the implications of a poor sample size calculation can render a study unethical, unpublishable, or both. For simple study designs undertaken in controlled settings, there is a wealth of evidence based guidance on sample size calculations for clinical trials, experimental studies, and various types of rigorous analyses (Table 1 ), which can help make this process relatively straightforward. Although experimental trials (e.g., testing new treatment methods) are undertaken within health care settings, research to further understand and improve the health service itself is often cross-sectional, involves no intervention, and is likely to be observing multiple associations [ 4 ]. For example, testing the association between leadership on hospital wards and patient re-admission, controlling for various factors such as ward speciality, size of team, and staff turnover, would likely involve collecting a variety of data (e.g., personal information, surveys, administrative data) at one time point, with no experimental group or single hypothesis. Multi-method study designs of this type create challenges, as inputs for an adequate sample size calculation are often not readily available. These inputs are typically: defined groups for comparison, a hypothesis about the difference in outcome between the groups (an effect size), an estimate of the distribution of the outcome (variance), and desired levels of significance and power to find these differences (Fig. 2 ).

References for sample size calculation

Primer = basic paper on the concepts around sample size determination, provides a basic but important understanding. Concepts = provides a more detailed explanation around specific aspects of sample size calculation. Sample size = these papers provide examples of sample size calculation for specific analysis types. ROT = these papers provide sample size ‘rules of thumb’ for one or more type of analysis. Simulation = these papers report the results of sample size simulation for various types of analysis

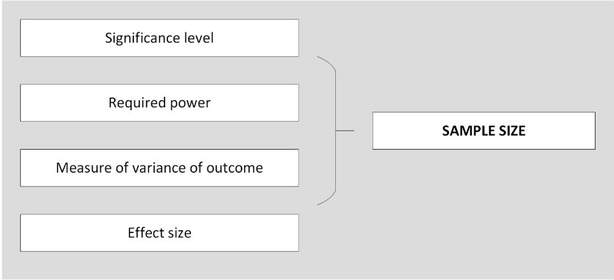
Inputs for a sample size calculation

Even in large studies there is often an absence of funding for statistical support, or the funding is inadequate for the size of the project [ 5 ]. This is particularly evident in the planning phase, which is arguably when it is required the most [ 6 ]. A study by Altman et al. [ 7 ] of statistician involvement in 704 papers submitted to the British Medical Journal and Annals of Internal Medicine indicated that only 51 % of observational studies received input from trained biostatisticians and, even when accounting for contributions from epidemiologists and other methodologists, only 52 % of observational studies utilized statistical advice in the study planning phase [ 7 ]. The practice of health services researchers performing their own statistical analysis without appropriate training or consultation from trained statisticians is not considered ideal [ 5 ]. In the review decisions of journal editors, manuscripts describing studies requiring statistical expertise are more likely to be rejected prior to peer review if the contribution of a statistician or methodologist has not been declared [ 7 ].

Calculating an appropriate sample size is not only to be considered a means to an end in obtaining accurate results. It is an important part of planning research, which will shape the eventual study design and data collection processes. Attacking the problem of sample size is also a good way of testing the validity of the study, confirming the research questions and clarifying the research to be undertaken and the potential outcomes. After all it is unethical to conduct research that is knowingly either overpowered or underpowered [ 2 , 3 ]. A study using more participants then necessary is a waste of resources and the time and effort of participants. An underpowered study is of limited benefit to the scientific community and is similarly wasteful.

With this in mind, it is surprising that methodologists such as statisticians are not customarily included in the study design phase. Whilst a lack of funding is partially to blame, it might also be that because sample size calculation and study design seem relatively simple on the surface, it is deemed unnecessary to enlist statistical expertise, or that it is only needed during the analysis phase. However, literature on sample size normally revolves around a single well defined hypothesis, an expected effect size, two groups to compare, and a known variance—an unlikely situation in practice, and a situation that can only occur with good planning. A well thought out study and analysis plan, formed in a conjunction with a statistician, can be utilized effectively and independently by researchers with the help of available literature. However a poorly planned study cannot be corrected by a statistician after the fact. For this reason a methodologist should be consulted early when designing the study.

Yet there is help if a statistician or methodologist is not available. The following steps provide useful information to aid researchers in designing their study and calculating sample size. Additionally, a list of resources (Table 1 ) that broadly frame sample size calculation is provided to guide researchers toward further literature searches. 1

A place to begin

Merrifield and Smith [ 1 ], and Martinez-Mesa et al. [ 3 ] discuss simple sample size calculations and explain the key concepts (e.g., power, effect size and significance) in simple terms and from a general health research perspective. These are a useful reference for non-statisticians and a good place to start for researchers who need a quick reminder of the basics. Lenth [ 2 ] provides an excellent and detailed exposition of effect size, including what one should avoid in sample size calculation.

Despite the guidance provided by this literature, there are additional factors to consider when determining sample size in health services research. Sample size requires deliberation from the outset of the study. Figure 3 depicts how different aspects of research are related to sample size and how each should be considered as part of an iterative planning phase. The components of this process are detailed below.

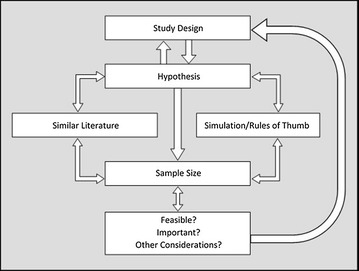
Stages in sample size calculation

Study design and hypothesis

The study design and hypothesis of a research project are two sides of the same coin. When there is a single unifying hypothesis, clear comparison groups and an effect size, e.g., drug A will reduce blood pressure 10 % more than drug B, then the study design becomes clear and the sample size can be calculated with relative ease. In this situation all the inputs are available for the diagram in Fig. 2 .

However, in large scale or complex health services research the aim is often to further our understanding about the way the system works, and to inform the design of appropriate interventions for improvement. Data collected for this purpose is cross-sectional in nature, with multiple variables within health care (e.g., processes, perceptions, outputs, outcomes, costs) collected simultaneously to build an accurate picture of a complex system. It is unlikely that there is a single hypothesis that can be used for the sample size calculation, and in many cases much of the hypothesising may not be performed until after some initial descriptive analysis. So how does one move forward?

To begin, consider your hypothesis (one or multiple). What relationships do you want to find specifically? There are three reasons why you may not find the relationships you are looking for:

The relationship does not exist.

The study was not adequately powered to find the relationship.

The relationship was obscured by other relationships.

There is no way to avoid the first, avoiding the second involves a good understanding of power and effect size (see Lenth [ 2 ]), and avoiding the third requires an understanding of your data and your area of research. A sample size calculation needs to be well thought out so that the research can either find the relationship, or, if one is not found, to be clear why it wasn’t found. The problem remains that before an estimate of the effect size can be made, a single hypothesis, single outcome measure and study design is required. If there is more than one outcome measure, then each requires an independent sample size calculation as each outcome measure has a unique distribution. Even with an analysis approach confirmed (e.g., a multilevel model), it can be difficult to decide which effect size measure should be used if there is a lack of research evidence in the area, or a lack of consensus within the literature about which effect sizes are appropriate. For example, despite the fact that Lenth advises researchers to avoid using Cohen’s effect size measurements [ 2 ], these margins are regularly applied [ 8 ].

To overcome these challenges, the following processes are recommended:

Select a primary hypothesis. Although the study may aim to assess a large variety of outcomes and independent variables, it is useful to consider if there is one relationship that is of most importance. For example, for a study attempting to assess mortality, re-admissions and length of stay as outcomes, each outcome will require its own hypothesis. It may be that for this particular study, re-admission rates are most important, therefore the study should be powered first and foremost to address that hypothesis. Walker [ 9 ] describes why having a single hypothesis is easier to communicate and how the results for primary and secondary hypotheses should be reported.

Consider a set of important hypotheses and the ways in which you might have to answer each one. Each hypothesis will likely require different statistical tests and methods. Take the example of a study aiming to understand more about the factors associated with hospital outcomes through multiple tests for associations between outcomes such as length of stay, mortality, and readmission rates (dependent variables) and nurse experience, nurse-patient ratio and nurse satisfaction (independent variables). Each of these investigations may use a different type of analysis, a different statistical test, and have a unique sample size requirement. It would be possible to roughly calculate the requirements and select the largest one as the overall sample size for the study. This way, the tests that require smaller samples are sure to be adequately powered. This option requires more time and understanding than the first.

During the study planning phase, when a literature review is normally undertaken, it is important not only to assess the findings of previous research, but also the design and the analysis. During the literature review phase, it is useful to keep a record of the study designs, outcome measures, and sample sizes that have already been reported. Consider whether those studies were adequately powered by examining the standard errors of the results and note any reported variances of outcome variables that are likely to be measured.

One of the most difficult challenges is to establish an appropriate expected effect size. This is often not available in the literature and has to be a judgement call based on experience. However previous studies may provide insight into clinically significant differences and the distribution of outcome measures, which can be used to help determine the effect size. It is recommended that experts in the research area are consulted to inform the decision about the expected effect size [ 2 , 8 ].

Simulation and rules of thumb

For many study designs, simulation studies are available (Table 1 ). Simulation studies generally perform multiple simulated experiments on fictional data using different effect sizes, outcomes and sample sizes. From this, an estimation of the standard error and any bias can be identified for the different conditions of the experiments. These are great tools and provide ‘ball park’ figures for similar (although most likely not identical) study designs. As evident in Table 1 , simulation studies often accompany discussions of sample size calculations. Simulation studies also provide ‘rules of thumb’, or heuristics about certain study designs and the sample required for each one. For example, one rule of thumb dictates that more than five cases per variable are required for a regression analysis [ 10 ].

Before making a final decision on a hypothesis and study design, identify the range of sample sizes that will be required for your research under different conditions. Early identification of a sample size that is prohibitively large will prevent time being wasted designing a study destined to be underpowered. Importantly, heuristics should not be used as the main source of information for sample size calculation. Rules of thumb are rarely congruous with careful sample size calculation [ 10 ] and will likely lead to an underpowered study. They should only be used, along with the information gathered through the use of the other techniques recommended in this paper, as a guide to inform the hypothesis and study design.

Other considerations

Be mindful of multiple comparisons.

The nature of statistical significance is that one in every 20 hypotheses tested will give a (false) significant result. This should be kept in mind when running multiple tests on the collected data. The hypothesis and appropriate tests should be nominated before the data are collected and only those tests should be performed. There are ways to correct for multiple comparisons [ 9 ], however, many argue that this is unnecessary [ 11 ]. There is no definitive way to ‘fix’ the problem of multiple tests being performed on a single data set and statisticians continue to argue over the best methodology [ 12 , 13 ]. Despite its complexity, it is worth considering how multiple comparisons may affect the results, and if there would be a reasonable way to adjust for this. The decision made should be noted and explained in the submitted manuscript.

After reading some introductory literature around sample size calculation it should be possible to derive an estimate to meet the study requirements. If this sample is not feasible, all is not lost. If the study is novel, it may add to the literature regardless of sample size. It may be possible to use pilot data from this preliminary work to compute a sample size calculation for a future study, to incorporate a qualitative component (e.g., interviews, focus groups), for answering a research question, or to inform new research.

Post hoc power analysis

This involves calculating the power of the study retrospectively, by using the observed effect size in the data collected to add interpretation to an insignificant result [ 2 ]. Hoenig and Heisey [ 14 ] detail this concept at length, including the range of associated limitations of such an approach. The well-reported criticisms of post hoc power analysis should cultivate research practice that involves appropriate methodological planning prior to embarking on a project.

Health services research can be a difficult environment for sample size calculation. However, it is entirely possible that, provided that significance, power, effect size and study design have been appropriately considered, a logical, meaningful and defensible calculation can always be obtained, achieving the situation described in Fig. 4 .

A statistician’s dream

Authors’ contributions

VP drafted the paper, performed literature searches and tabulated the findings. NT made substantial contribution to the structure and contents of the article. RCW provided assistance with the figures and tables, as well as structure and contents of the article. Both RCW and NT aided in the analysis and interpretation of findings. JB provided input into the conception and design of the article and critically reviewed its contents. All authors read and approved the final manuscript.

Acknowledgements

We would like to acknowledge Emily Hogden for assistance with editing and submission. The funding source for this article is an Australian National Health and Medical Research Council (NHMRC) Program Grant, APP1054146.

Authors’ information

VP is a biostatistician with 7 years’ experience in health research settings. NT is a health psychologist with organizational behaviour change and implementation expertise. RCW is a health services researcher with expertise in human factors and systems thinking. JB is a professor of health services research and Foundation Director of the Australian Institute of Health Innovation.

Competing interests

The authors declare that they have no competing interests.

Additional file

10.1186/s13104-016-1893-x Case study. This case study illustrates the steps of a sample size calculation.

Literature summarising an aspect of sample size calculation is included in Table 1 , providing a comprehensive mix of different aspects. The list is not exhaustive, and is to be used as a starting point to allow researchers to perform a more targeted search once their sample size problems have become clear. A librarian was consulted to inform a search strategy, which was then refined by the lead author. The resulting literature was reviewed by the lead author to ascertain suitability for inclusion.

Contributor Information

Victoria Pye, Email: [email protected].

Natalie Taylor, Email: [email protected].

Robyn Clay-Williams, Email: [email protected].

Jeffrey Braithwaite, Email: [email protected].

1. Merrifield A, Smith W. Sample size calculations for the design of health studies: a review of key concepts for non-statisticians. NSW Public Health Bull. 2012;23(8):142–147. doi: 10.1071/NB11017. [ DOI ] [ PubMed ] [ Google Scholar ]
2. Lenth RV. Some practical guidelines for effective sample size determination. Am Stat. 2001;55(3):187–193. doi: 10.1198/000313001317098149. [ DOI ] [ Google Scholar ]
3. Martinez-Mesa J, Gonzalez-Chica DA, Bastos JL, Bonamigo RR, Duquia RP. Sample size: how many participants do i need in my research? An Bras Dermatol. 2014;89(4):609–615. doi: 10.1590/abd1806-4841.20143705. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
4. Webb P, Bain C. Essential epidemiology: an introduction for students and health professionals. 2. Cambridge: Cambridge University Press; 2011. [ Google Scholar ]
5. Omar RZ, McNally N, Ambler G, Pollock AM. Quality research in healthcare: are researchers getting enough statistical support? BMC Health Serv Res. 2006;6:2. doi: 10.1186/1472-6963-6-2. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
6. Maxwell SE, Kelley K, Rausch JR. Sample size planning for statistical power and accuracy in parameter estimation. Annu Rev Psychol. 2008;59:537–563. doi: 10.1146/annurev.psych.59.103006.093735. [ DOI ] [ PubMed ] [ Google Scholar ]
7. Altman DG, Goodman SN, Schroter S. How statistical expertise is used in medical research. J Am Med Assoc. 2002;287(21):2817–2820. doi: 10.1001/jama.287.21.2817. [ DOI ] [ PubMed ] [ Google Scholar ]
8. Sullivan GM, Feinn R. Using effect size—or why the P value is not enough. J Grad Med Educ. 2012;4(3):279–282. doi: 10.4300/JGME-D-12-00156.1. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
9. Walker AM. Reporting the results of epidemiologic studies. Am J Public Health. 1986;76(5):556–558. doi: 10.2105/AJPH.76.5.556. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
10. Green SB. How many subjects does it take to do a regression analysis. Multivariate Behav Res. 1991;26(3):499–510. doi: 10.1207/s15327906mbr2603_7. [ DOI ] [ PubMed ] [ Google Scholar ]
11. Feise R. Do multiple outcome measures require p-value adjustment? BMC Med Res Methodol. 2002;2(1):8. doi: 10.1186/1471-2288-2-8. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
12. Savitz DA, Olshan AF. Describing data requires no adjustment for multiple comparisons: a reply from Savitz and Olshan. Am J Epidemiol. 1998;147(9):813–814. doi: 10.1093/oxfordjournals.aje.a009532. [ DOI ] [ PubMed ] [ Google Scholar ]
13. Savitz DA, Olshan AF. Multiple comparisons and related issues in the interpretation of epidemiologic data. Am J Epidemiol. 1995;142(9):904–908. doi: 10.1093/oxfordjournals.aje.a117737. [ DOI ] [ PubMed ] [ Google Scholar ]
14. Hoenig JM, Heisey DM. The abuse of power: the pervasive fallacy of power calculations for data analysis. Am Stat. 2001;55(1):19–24. doi: 10.1198/000313001300339897. [ DOI ] [ Google Scholar ]
15. Noordzij M, Tripepi G, Dekker FW, Zoccali C, Tanck MW, Jager KJ. Sample size calculations: basic principles and common pitfalls. Nephrol Dial Transplant. 2010;25(5):1388–1393. doi: 10.1093/ndt/gfp732. [ DOI ] [ PubMed ] [ Google Scholar ]
16. Vardeman SB, Morris MD. Statistics and ethics: some advice for young statisticians. Am Stat. 2003;57(1):21–26. doi: 10.1198/0003130031072. [ DOI ] [ Google Scholar ]
17. Dowd BE. Separated at birth: statisticians, social scientists, and causality in health services research. Health Serv Res. 2011;46(2):397–420. doi: 10.1111/j.1475-6773.2010.01203.x. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
18. Dimick JB, Welch HG, Birkmeyer JD. Surgical mortality as an indicator of hospital quality: the problem with small sample size. J Am Med Assoc. 2004;292(7):847–851. doi: 10.1001/jama.292.7.847. [ DOI ] [ PubMed ] [ Google Scholar ]
19. Thomas DC, Siemiatycki J, Dewar R, Robins J, Goldberg M, Armstrong BG. The problem of multiple inference in studies designed to generate hypotheses. Am J Epidemiol. 1985;122(6):1080–1095. doi: 10.1093/oxfordjournals.aje.a114189. [ DOI ] [ PubMed ] [ Google Scholar ]
20. VanVoorhis CW, Morgan BL. Understanding power and rules of thumb for determining sample sizes. Tutor Quant Methods Psychol. 2007;3(2):43–50. [ Google Scholar ]
21. Van Belle G. Statistical rules of thumb. 2. New York: Wiley; 2011. [ Google Scholar ]
22. Serumaga-Zake PA, Arnab R, editors. A suggested statistical procedure for estimating the minimum sample size required for a complex cross-sectional study. The 7th international multi-conference on society, cybernetics and informatics: IMSCI, 2013 Orlando, Florida, USA; 2013.
23. Hsieh FY, Bloch DA, Larsen MD. A simple method of sample size calculation for linear and logistic regression. Stat Med. 1998;17(14):1623–1634. doi: 10.1002/(SICI)1097-0258(19980730)17:14<1623::AID-SIM871>3.0.CO;2-S. [ DOI ] [ PubMed ] [ Google Scholar ]
24. Alam MK, Rao MB, Cheng F-C. Sample size determination in logistic regression. Sankhya B. 2010;72(1):58–75. doi: 10.1007/s13571-010-0004-6. [ DOI ] [ Google Scholar ]
25. Peduzzi P, Concato J, Kemper E, Holford TR, Feinstein AR. A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol. 1996;49(12):1373–1379. doi: 10.1016/S0895-4356(96)00236-3. [ DOI ] [ PubMed ] [ Google Scholar ]
26. Dupont WD, Plummer WD., Jr Power and sample size calculations for studies involving linear regression. Control Clin Trials. 1998;19(6):589–601. doi: 10.1016/S0197-2456(98)00037-3. [ DOI ] [ PubMed ] [ Google Scholar ]
27. Zhong B. How to calculate sample size in randomized controlled trial? J Thorac Dis. 2009;1(1):51–54. [ PMC free article ] [ PubMed ] [ Google Scholar ]
28. Maas CJM, Hox JJ. Sufficient sample sizes for multilevel modeling. Methodology. 2005;1(3):86–92. doi: 10.1027/1614-2241.1.3.86. [ DOI ] [ Google Scholar ]
29. Cohen MP. Sample size considerations for multilevel surveys. Int Stat Rev. 2005;73(3):279–287. doi: 10.1111/j.1751-5823.2005.tb00149.x. [ DOI ] [ Google Scholar ]
30. Paccagnella O. Sample size and accuracy of estimates in multilevel models: new simulation results. Methodology. 2011;7(3):111–120. doi: 10.1027/1614-2241/a000029. [ DOI ] [ Google Scholar ]
31. Maas CJM, Hox JJ. Robustness issues in multilevel regression analysis. Stat Neerl. 2004;58(2):127–137. doi: 10.1046/j.0039-0402.2003.00252.x. [ DOI ] [ Google Scholar ]
View on publisher site
PDF (1.4 MB)
Collections

Add to Collections

How To Determine Sample Size for Quantitative Research

This blog post looks at how large a sample size should be for reliable, usable market research findings.

Jan 29, 2024

quantilope is the Consumer Intelligence Platform for all end-to-end research needs

You need to determine how big of a sample size you need so that you can be sure the quantitative data you get from a survey is reflective of your target population as a whole - and so that the decisions you make based on the research have a firm foundation. Too big a sample and a project can be needlessly expensive and time-consuming. Too small a sample size, and you risk interviewing the wrong respondents - meaning ultimately you miss out on valuable insights.

There are a few variables to be aware of before working out the right sample size for your project.

Population size

The subject matter of your research will determine who your respondents are - chocolate eaters, dentists, homeowners, drivers, people who work in IT, etc. For your respective group of interest, the total of this target group (i.e. the number of chocolate eaters/homeowners/drivers that exist in the general population) will guide how many respondents you need to interview for reliable results in that field.

Ideally, you would use a random sample of people who fit within the group of people you’re interested in. Some of these people are easy to get hold of, while others aren‘t as easy. Some represent smaller groups of people in the population, so a small sample is inevitable. For example, if you’re interviewing chocolate eaters aged 5-99 you’ll have a larger sample size - and a much easier time sampling the population - than if you’re interviewing healthcare professionals who specialize in a niche branch of medicine.

Confidence interval (margin of error)

Confidence intervals, otherwise known as the margin of error, indicate the reliability of statistics that have been calculated by research; in other words, how certain you can be that the statistics are close to what they would be if it were possible to interview the entire population of the people you’re researching.

Confidence intervals are helpful since it would be impossible to interview all chocolate eaters in the US. However, statistics and research enable you to take a sample of that group and achieve results that reflect their opinions as a total population. Before starting a research project, you can decide how large a margin of error you will allow between the mean number of your sample and the mean number of its total population. The confidence interval is expressed as +/- a number, indicating the margin of error on either side of your statistic. For example, if 35% of chocolate eaters say that they eat chocolate for breakfast and your margin of error is 5, you’ll know that if you had asked the entire population, 30-40% of people would admit to eating chocolate at that time of day.

Confidence level

The confidence level indicates how probable it is that if you were to repeat your study multiple times with a random sample, you would get the same statistics and they would fall within the confidence interval every time.

In the example above, if you were to repeat the chocolate study over and over, you would have a certain level of confidence that those eating chocolate for breakfast would always fall within the 30-40% parameters. Most research studies have confidence intervals of 90% confident, 95% confident, or 99% confident. The number you choose will depend on whether you are happy to accept a broadly accurate set of data or whether the nature of your study demands one that is almost completely reliable.

Standard deviation

Standard deviation represents how much the results will vary from the mean number and from each other. A high standard deviation means that there is a wide range of responses to your research questions, while a low standard deviation indicates that responses are more similar to each other, clustered around the mean number. A standard deviation of 0.5 is a safe level to pick to ensure that the sample size is large enough.

Population variability

If you already know anything about your target audience, you should have a feel for the degree to which their opinions vary. If you’re interviewing the entire population of a city, without any other criteria, their views are going to be wildly diverse so you’ll want to sample a high number of residents. If you’re honing in on a sample of chocolate breakfast eaters - there’s probably a limited number of reasons why that’s their meal of choice, so you can feel confident with a much smaller sample.

Project scope

The scope and objectives of the research will have an influence on how big the sample is. If the project aims to evaluate four different pieces of stimulus (an advert, a concept, a website, etc.) and each respondent is giving feedback on a single piece, then a higher number of respondents will need to be interviewed than if each respondent were evaluating all four; the same would be true when looking for reads on four different sub-audiences vs. not needing any sub-group data cuts.

Determining a good sample size for quantitative research

Sample size, as we’ve seen, is an important factor to consider in market research projects. Getting the sample size right will result in research findings you can use confidently when translating them into action. So now that you’ve thought about the subject of your research, the population that you’d like to interview, and how confident you want to be with the findings, how do you calculate the appropriate sample size?

There are many factors that can go into determining the sample size for a study, including z-scores, standard deviations, confidence levels, and margins of error. The great thing about quantilope is that your research consultants and data scientists are the experts in helping you land on the right target so you can focus on the actual study and the findings.

To learn more about determining sample size for quantitative research, get in touch below:

Get in touch to learn more about quantitative sample sizes!

Essential Brand Tracking Metrics

This blog covers brand health tracking - from traditional brand health studies to the more advanced Better Brand Health Tracking (BBHT).

October 15, 2024

The Power of Shopper Insights

In this post, we explore consumer shopper insights and shopper insights examples to highlight how brands can benefit from this type of mark...

October 14, 2024

Wave 7 of quantilope's Direct-to-Consumer (DTC) Mattress Tracker

Wave 7 of quantilope's DTC mattress tracker includes the recent addition of Better Brand Health Tracking's Mental Advantage analysis to fue...

October 02, 2024

Forgot Password?

Sample size in quantitative research: Sample size will affect the significance of your research

Citation metadata, document controls, main content.

YOU'VE probably been asked (or have asked) the question: How many subjects do I need for my research study? That's your sample size--the number of participants needed to achieve valid conclusions or statistical significance in quantitative research. (Qualitative research requires a somewhat different approach.

In this article, we'll answer these questions about sample size in quantitative research: Why does sample size matter? How do I determine sample size? Which sampling method should I use? What's sampling bias?

Why does sample size matter?

When sample sizes are too small, you run the risk of not gathering enough data to support your hypotheses or expectations. The result may indicate that relationships between variables aren't statistically significant when, actually, they are. You also may be missing subjects who might give a different answer or perspective to your survey or interview. Samples that are too large may provide data that describe associations or relationships that are due merely to chance. Large samples also may waste time and money.

How do I determine sample size?

Larger sample sizes typically are more representative of the population you're studying, but only if you collect data randomly and the population is heterogeneous. Large samples also reduce the chance of outliers. However, large samples are no guarantee of accuracy. If your population of interest is homogenous, you may need only a small sample.

If you're studying subjects over longer periods of time, as in longitudinal designs, you can expect subject attrition. Know your population and how responsive they may be to repeated questionnaires and interventions. Even if you're not conducting a longitudinal study, be realistic about how many people would agree to participate in research....

Source Citation

Gale Document Number: GALE|A592663691

Report an Issue

Submitted diagnostic report.

Timestamp: October 25, 2024 at 6:07:38 AM EDT

Ticket Number:

Reporter's Email:

Reporter's Name:

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

Publications
Account settings
Advanced Search
Journal List

Statistics in Brief: The Importance of Sample Size in the Planning and Interpretation of Medical Research

David jean biau , md, solen kernéis , md, raphaël porcher , phd.

Author information
Article notes
Copyright and License information

Corresponding author.

Received 2007 Nov 1; Accepted 2008 May 22; Issue date 2008 Sep.

The increasing volume of research by the medical community often leads to increasing numbers of contradictory findings and conclusions. Although the differences observed may represent true differences, the results also may differ because of sampling variability as all studies are performed on a limited number of specimens or patients. When planning a study reporting differences among groups of patients or describing some variable in a single group, sample size should be considered because it allows the researcher to control for the risk of reporting a false-negative finding (Type II error) or to estimate the precision his or her experiment will yield. Equally important, readers of medical journals should understand sample size because such understanding is essential to interpret the relevance of a finding with regard to their own patients. At the time of planning, the investigator must establish (1) a justifiable level of statistical significance, (2) the chances of detecting a difference of given magnitude between the groups compared, ie, the power, (3) this targeted difference (ie, effect size), and (4) the variability of the data (for quantitative data). We believe correct planning of experiments is an ethical issue of concern to the entire community.

Introduction

“Statistical analysis allows us to put limits on our uncertainty, but not to prove anything.”— Douglas G. Altman [ 1 ]

The growing need for medical practice based on evidence has generated an increasing medical literature supported by statistics: readers expect and presume medical journals publish only studies with unquestionable results they can use in their everyday practice and editors expect and often request authors provide rigorously supportable answers. Researchers submit articles based on presumably valid outcome measures, analyses, and conclusions claiming or implying the superiority of one treatment over another, the usefulness of a new diagnostic test, or the prognostic value of some sign. Paradoxically, the increasing frequency of seemingly contradictory results may be generating increasing skepticism in the medical community.

One fundamental reason for this conundrum takes root in the theory of hypothesis testing developed by Pearson and Neyman in the late 1920s [ 24 , 25 ]. The majority of medical research is presented in the form of a comparison, the most obvious being treatment comparisons in randomized controlled trials. To assess whether the difference observed is likely attributable to chance alone or to a true difference, researchers set a null hypothesis that there is no difference between the alternative treatments. They then determine the probability (the p value), they could have obtained the difference observed or a larger difference if the null hypothesis were true; if this probability is below some predetermined explicit significance level, the null hypothesis (ie, there is no difference) is rejected. However, regardless of study results, there is always a chance to conclude there is a difference when in fact there is not (Type I error or false positive) or to report there is no difference when a true difference does exist (Type II error or false negative) and the study has simply failed to detect it (Table 1 ). The size of the sample studied is a major determinant of the risk of reporting false-negative findings. Therefore, sample size is important for planning and interpreting medical research.

Type I and Type II errors during hypothesis testing

For that reason, we believe readers should be adequately informed of the frequent issues related to sample size, such as (1) the desired level of statistical significance, (2) the chances of detecting a difference of given magnitude between the groups compared, ie, the power, (3) this targeted difference, and (4) the variability of the data (for quantitative data). We will illustrate these matters with a comparison between two treatments in a surgical randomized controlled trial. The use of sample size also will be presented in other common areas of statistics, such as estimation and regression analyzes.

Desired Level of Significance

The level of statistical significance α corresponds to the probability of Type I error, namely, the probability of rejecting the null hypothesis of “no difference between the treatments compared” when in fact it is true. The decision to reject the null hypothesis is based on a comparison of the prespecified level of the test arbitrarily chosen with the test procedure’s p value. Controlling for Type I error is paramount to medical research to avoid the spread of new or perpetuation of old treatments that are ineffective. For the majority of hypothesis tests, the level of significance is arbitrarily chosen at 5%. When an investigator chooses α = 5%, if the test’s procedure p value computed is less than 5%, the null hypothesis will be rejected and the treatments compared will be assumed to be different.

To reduce the probability of Type I error, we may choose to reduce the level of statistical significance to 1% or less [ 29 ]. However, the level of statistical significance also influences the sample size calculation: the lower the chosen level of statistical significance, the larger the sample size will be, considering all other parameters remain the same (see example below and Appendix 1). Consequently, there are domains where higher levels of statistical significance are used so that the sample size remains restricted, such as for randomized Phase II screening designs in cancer [ 26 ]. We believe the choice of a significance level greater than 5% should be restricted to particular cases.

The power of a test is defined as 1 − the probability of Type II error. The Type II error is concluding at no difference (the null is not rejected) when in fact there is a difference, and its probability is named β. Therefore, the power of a study reflects the probability of detecting a difference when this difference exists. It is also very important to medical research that studies are planned with an adequate power so that meaningful conclusions can be issued if no statistical difference has been shown between the treatments compared. More power means less risk for Type II errors and more chances to detect a difference when it exists.

Power should be determined a priori to be at least 80% and preferably 90%. The latter means, if the true difference between treatments is equal to the one we planned, there is only 10% chance the study will not detect it. Sample size increases with increasing power (Fig. 1 ).

The graphs show the distribution of the test statistic (z-test) for the null hypothesis (plain line) and the alternative hypothesis (dotted line) for a sample size of ( A ) 32 patients per group, ( B ) 64 patients per group, and ( C ) 85 patients per group. For a difference in mean of 10, a standard deviation of 20, and a significance level α of 5%, the power (shaded area) increases from ( A ) 50%, to ( B ) 80%, and ( C ) 90%. It can be seen, as power increases, the test statistics yielded under the alternative hypothesis (there is a difference in the two comparison groups) are more likely to be greater than the critical value 1.96.

Very commonly, power calculations have not been performed before conducting the trial [ 3 , 8 ], and when facing nonsignificant results, investigators sometimes compute post hoc power analyses, also called observed power. For this purpose, investigators use the observed difference and variability and the sample size of the trial to determine the power they would have had to detect this particular difference. However, post hoc power analyses have little statistical meaning for three reasons [ 9 , 13 ]. First, because there is a one-to-one relationship between p values and post hoc power, the latter does not convey any additional information on the sample than the former. Second, nonsignificant p values always correspond to low power and post hoc power, at best, will be slightly larger than 50% for p values equal to or greater than 0.05. Third, when computing post hoc power, investigators implicitly make the assumption that the difference observed is clinically meaningful and more representative of the truth than the null hypothesis they precisely were not able to reject. However, in the theory of hypothesis testing, the difference observed should be used only to choose between the hypotheses stated a priori; a posteriori, the use of confidence intervals is preferable to judge the relevance of a finding. The confidence interval represents the range of values we can be confident to some extent includes the true difference. It is related directly to sample size and conveys more information than p values. Nonetheless, post hoc power analyses educate readers about the importance of considering sample size by explicitly raising the issue.

The Targeted Difference Between the Alternative Treatments

The targeted difference between the alternative treatments is determined a priori by the investigator, typically based on preliminary data. The larger the expected difference is, the smaller the required sample size will be. However, because the sample size based on the difference expected may be too large to achieve, investigators sometimes choose to power their trial to detect a difference larger than one would normally expect to reduce the sample size and minimize the time and resources dedicated to the trial. However, if the targeted difference between the alternative treatments is larger than the true difference, the trial may fail to conclude a difference between the two treatments when a smaller, and still meaningful, difference exists. This smallest meaningful difference sometimes is expressed as the “minimal clinically important difference,” namely, “the smallest difference in score in the domain of interest which patients perceive as beneficial and which would mandate, in the absence of troublesome side effects and excessive costs, a change in the patient’s management” [ 15 ]. Because theoretically the minimal clinically important difference is a multidimensional phenomenon that encompasses a wide range of complex issues of a particular treatment in a unique setting, it usually is determined by consensus among clinicians with expertise in the domain. When the measure of treatment effect is based on a score, researchers may use empiric definitions of clinically meaningful difference. For instance, Michener et al. [ 21 ], in a prospective study of 63 patients with various shoulder abnormalities, determined the minimal change perceived as clinically meaningful by the patients for the patient self-report section of the American Shoulder and Elbow Surgeons Standardized Shoulder Assessment Form was 6.7 points of 100 points. Similarly, Bijur et al. [ 5 ], in a prospective cohort study of 108 adults presenting to the emergency department with acute pain, determined the minimal change perceived as clinically meaningful by patients for acute pain measured on the visual analog scale was 1.4 points. There is no reason to try to detect a difference below the minimal clinically important difference because, even if it proves statistically significant, it will not be meaningful.

The meaningful clinically important difference should not be confused with the effect size. The effect size is a dimensionless measure of the magnitude of a relation between two or more variables, such as Cohen’s d standardized difference [ 6 ], but also odds ratio, Pearson’s r correlation coefficient, etc. Sometimes studies are planned to detect a particular effect size instead of being planned to detect a particular difference between the two treatments. According to Cohen [ 6 ], 0.2 is indicative of a small effect, 0.5 a medium effect, and 0.8 a large effect size. One of the advantages of doing so is that researchers do not have to make any assumptions regarding the minimal clinically important difference or the expected variability of the data.

The Variability of the Data

For quantitative data, researchers also need to determine the expected variability of the alternative treatments: the more variability expected in the specified outcome, the more difficult it will be to differentiate between treatments and the larger the required sample size (see example below). If this variability is underestimated at the time of planning, the sample size computed will be too small and the study will be underpowered to the one desired. For comparing proportions, the calculation of sample size makes use of the expected proportion with the specified outcome in each group. For survival data, the calculation of sample size is based on the survival proportions in each treatment group at a specified time and on the total number of events in the group in which the fewer events occur. Therefore, for the latter two types of data, variability does not appear in the computation of sample size.

Presume an investigator wants to compare the postoperative Harris hip score [ 12 ] at 3 months in a group of patients undergoing minimally invasive THA with a control group of patients undergoing standard THA in a randomized controlled trial. The investigator must (1) establish a statistical significance level, eg, α = 5%, (2) select a power, eg, 1 − β = 90%, and (3) establish a targeted difference in the mean scores, eg, 10, and assume a standard deviation of the scores, eg, 20 in both groups (which they can obtain from the literature or their previous patients). In this case, the sample size should be 85 patients per group (Appendix 1). If fewer patients are included in the trial, the probability of detecting the targeted difference when it exists will decrease; for sample sizes of 64 and 32 per group, for instance, the power decreases to 80% and 50%, respectively (Fig. 1 ). If the investigator assumed the standard deviation of the scores in each group to be 30 instead of 20, a sample size of 190 per group would be necessary to obtain a power of 90% with a significance level α = 5% and targeted difference in the mean scores of 10. If the significance level was chosen at α = 1% instead of α = 5%, to yield the same power of 90% with a targeted difference in scores of 10 and standard deviation of 20, the sample size would increase from 85 patients per group to 120 patients per group. In relatively simple cases, statistical tables [ 19 ] and dedicated software available from the internet may be used to determine sample size. In most orthopaedic clinical trials cases, sample size calculation is rather simple as above, but it will become more complex in other cases. The type of end points, the number of groups, the statistical tests used, whether the observations are paired, and other factors influence the complexity of the calculation, and in these cases, expert statistical advice is recommended.

Sample Size, Estimation, and Regression

Sample size was presented above in the context of hypothesis testing. However, it is also of interest in other areas of biostatistics, such as estimation or regression. When planning an experiment, researchers should ensure the precision of the anticipated estimation will be adequate. The precision of an estimation corresponds to the width of the confidence interval: the larger the tested sample size is, the better the precision. For instance, Handl et al. [ 11 ], in a biomechanical study of 21 fresh-frozen cadavers, reported a mean ultimate load failure of four-strand hamstring tendon constructs of 4546 N under loading with a standard deviation of 1500 N. Based on these values, if we were to design an experiment to assess the ultimate load failure of a particular construct, the precision around the mean at the 95% confidence level would be expected to be 3725 N for five specimens, 2146 N for 10 specimens, 1238 N for 25 specimens, 853 N for 50 specimens, and 595 N for 100 specimens tested (Appendix 2); if we consider the estimated mean will be equal to 4546 N, the one obtained in the previous experiment, we could obtain the corresponding 95% confidence intervals (Fig. 2 ). Because we always deal with limited samples, we never exactly know the true mean or standard deviation of the parameter distribution; otherwise, we would not perform the experiment. We only approximate these values, and the results obtained can vary from the planned experiment. Nonetheless, what we identify at the time of planning is that testing more than 50 specimens, for instance 100, will multiply the costs and time necessary to the experiment while providing only slight improvement in the precision.

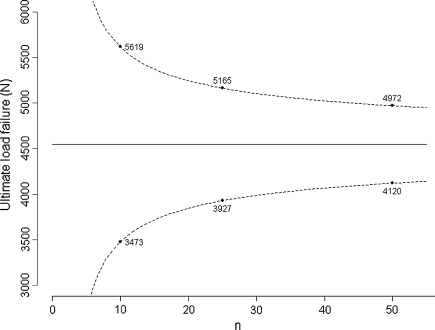
The graph shows the predicted confidence interval for experiments with an increasing number of specimens tested based on the study by Handl et al. [ 11 ] of 21 fresh-frozen cadavers with a mean ultimate load failure of four-strand hamstring tendon constructs of 4546 N and standard deviation of 1500 N.

Similarly, sample size issues should be considered when performing regression analyses, namely, when trying to assess the effect of a particular covariate, or set of covariates, on an outcome. The effective power to detect the significance of a covariate in predicting this outcome depends on the outcome modeled [ 14 , 30 ]. For instance, when using a Cox regression model, the power of the test to detect the significance of a particular covariate does not depend on the size of the sample per se but on the number of specific critical events. In a cohort study of patients treated for soft tissue sarcoma with various treatments, such as surgery, radiotherapy, chemotherapy, etc, the power to detect the effect of chemotherapy on survival will depend on the number of patients who die, not on the total number of patients in the cohort. Therefore, when planning such studies, researchers should be familiar with these issues and decide, for example, to model a composite outcome, such as event-free survival that includes any of the following events: death from disease, death from other causes, recurrence, metastases, etc, to increase the power of the test.

The reasons to plan a trial with an adequate sample size likely to give enough power to detect a meaningful difference are essentially ethical. Small trials are considered unethical by most, but not all, researchers because they expose participants to the burdens and risks of human research with a limited chance to provide any useful answers [ 2 , 10 , 28 ]. Underpowered trials also ineffectively consume resources (human, material) and add to the cost of healthcare to society. Although there are particular cases when trials conducted on a small sample are justified, such as early-phase trials with the aim of guiding the conduct of subsequent research (or formulating hypotheses) or, more rarely, for rare diseases with the aim of prospectively conducting meta-analyses, they generally should be avoided [ 10 ]. It is also unethical to conduct trials with too large a sample size because, in addition to the waste of time and resources, they expose participants in one group to receive inadequate treatment after appropriate conclusions should have been reached. Interim analyses and adaptive trials have been developed in this context to shorten the time to decision and overcome these concerns [ 4 , 16 ].

We raise two important points. First, we explained, for practical and ethical reasons, experiments are conducted on a sample of limited size with the aim to generalize the results to the population of interest and increasing the size of the sample is a way to combat uncertainty. When doing this, we implicitly consider the patients or specimens in the sample are randomly selected from the population of interest, although this is almost never the case; even if it were the case, the population of interest would be limited in space and time. For instance, Marx et al. [ 20 ], in a survey conducted in late 1998 and early 1999, assessed the practices for anterior cruciate ligament reconstruction on a randomly selected sample of 725 members of the American Academy of Orthopaedic Surgeons; however, because only ½ the surgeons responded to the survey, their sample probably is not representative of all members of the society, who in turn are not representative of all orthopaedic surgeons in the United States, who again are not representative of all surgeons in the world because of the numerous differences among patients, doctors, and healthcare systems across countries. Similar surveys conducted in other countries have provided different results [ 17 , 22 ]. Moreover, if the same survey was conducted today, the results would possibly differ. Therefore, another source for variation among studies, apart from sampling variability, is that samples may not be representative of the same population. Therefore, when planning experiments, researchers must take care to make their sample representative of the population they want to infer to and readers, when interpreting the results of a study, should always assess first how representative the sample presented is regarding their own patients. The process implemented to select the sample, the settings of the experiment, and the general characteristics and influencing factors of the patients must be described precisely to assess representativeness and possible selection biases [ 7 ].

Second, we have discussed only sample size for interpreting nonsignificant p values, but it also may be of interest when interpreting p values that are significant. Significant results issued from larger studies usually are given more credit than those from smaller studies because of the risk of reporting exaggerating treatment effects with studies with smaller samples or of lower quality [ 23 , 27 ], and small trials are believed to be more biased than others. However, there is no statistical reason a significant result in a trial including 2000 patients should be given more belief than a trial including 20 patients, given the significance level chosen is the same in both trials. Small but well-conducted trials may yield a reliable estimation of treatment effect. Kjaergard et al. [ 18 ], in a study of 14 meta-analyses involving 190 randomized trials, reported small trials (fewer than 1000 patients) reported exaggerated treatment effects when compared with large trials. However, when considering only small trials with adequate randomization, allocation concealment (allocation concealment is the process that keeps clinicians and participants unaware of upcoming assignments. Without it, even properly developed random allocation sequences can be subverted), and blinding, this difference became negligible. Nonetheless, the advantages of a large sample size to interpret significant results are it allows a more precise estimate of the treatment effect and it usually is easier to assess the representativeness of the sample and to generalize the results.

Sample size is important for planning and interpreting medical research and surgeons should become familiar with the basic elements required to assess sample size and the influence of sample size on the conclusions. Controlling for the size of the sample allows the researcher to walk a thin line that separates the uncertainty surrounding studies with too small a sample size from studies that have failed practical or ethical considerations because of too large a sample size.

Acknowledgments

We thank the editor whose thorough readings of, and accurate comments on drafts of the manuscript have helped clarify the manuscript.

The sample size (n) per group for comparing two means with a two-sided two-sample t test is

where z 1−α/2 and z 1−β are standard normal deviates for the probability of 1 − α/2 and 1 − β, respectively, and d t = (μ 0 − μ 1 )/σ is the targeted standardized difference between the two means.

The following values correspond to the example:

α = 0.05 (statistical significance level)

β = 0.10 (power of 90%)

|μ 0 − μ 1 | = 10 (difference in the mean score between the two groups)

σ = 20 (standard deviation of the score in each group)

z 1−α/2 = 1.96

z 1−β = 1.28

Two-sided tests which do not assume the direction of the difference (ie, that the mean value in one group would always be greater than that in the other) are generally preferred. The null hypothesis makes the assumption that there is no difference between the treatments compared, and a difference on one side or the other therefore is expected.

Computation of Confidence Interval

To determine the estimation of a parameter, or alternatively the confidence interval, we use the distribution of the parameter estimate in repeated samples of the same size. For instance, consider a parameter with observed mean, m, and standard deviation, sd, in a given sample. If we assume that the distribution of the parameter in the sample is close to a normal distribution, the means, x n , of several repeated samples of the same size have true mean, μ, the population mean, and estimated standard deviation,

also known as standard error of the mean, and

follows a t distribution. For a large sample, the t distribution becomes close to the normal distribution; however, for a smaller sample size the difference is not negligible and the t distribution is preferred. The precision of the estimation is

and the confidence interval for μ is the range of values extending either side of the sample mean m by

For example, Handl et al. [ 11 ] in a biomechanical study of 21 fresh-frozen cadavers reported a mean ultimate load failure of 4-strand hamstring tendon constructs of 4546 N under dynamic loading with standard deviation of 1500 N. If we were to plan an experiment, the anticipated precision of the estimation at the 95% level would be

for five specimens,

The values 2.78, 2.26, 2.06, 2.01, and 1.98 correspond to the t distribution deviates for the probability of 1 − α/2, with 4, 9, 24, 49, and 99 (n − 1) degrees of freedom; the well known corresponding standard normal deviate is 1.96. Given an estimated mean of 4546 N, the corresponding 95% confidence intervals are 2683 N to 6408 N for five specimens, 3473 N to 5619 N for 10 specimens, 3927 N to 5165 N for 25 specimens, 4120 N to 4972 N for 50 specimens, and 4248 N to 4844 N for 100 specimens (Fig. 2 ).

Similarly, for a proportion p in a given sample with sufficient sample size to assume a nearly normal distribution, the confidence interval extends either side of the proportion p by

For a small sample size, exact confidence interval for proportions should be used.

Each author certifies that he or she has no commercial associations (eg, consultancies, stock ownership, equity interest, patent/licensing arrangements, etc) that might pose a conflict of interest in connection with the submitted article.

1. Altman DG. Practical Statistics for Medical Research. London, UK: Chapman & Hall; 1991.
2. Bacchetti P, Wolf LE, Segal MR, McCulloch CE. Ethics and sample size. Am J Epidemiol. 2005;161:105–110. [ DOI ] [ PubMed ]
3. Bailey CS, Fisher CG, Dvorak MF. Type II error in the spine surgical literature. Spine. 2004;29:1146–1149. [ DOI ] [ PubMed ]
4. Bauer P, Brannath W. The advantages and disadvantages of adaptive designs for clinical trials. Drug Discov Today. 2004;9:351–357. [ DOI ] [ PubMed ]
5. Bijur PE, Latimer CT, Gallagher EJ. Validation of a verbally administered numerical rating scale of acute pain for use in the emergency department. Acad Emerg Med. 2003;10:390–392. [ DOI ] [ PubMed ]
6. Cohen J. Statistical Power Analysis for the Behavioral Sciences. 2nd ed. Hillsdale, NJ: Lawrence Earlbaum Associates; 1988.
7. Ellenberg JH. Selection bias in observational and experimental studies. Stat Med. 1994;13:557–567. [ DOI ] [ PubMed ]
8. Freedman KB, Back S, Bernstein J. Sample size and statistical power of randomised, controlled trials in orthopaedics. J Bone Joint Surg Br. 2001;83:397–402. [ DOI ] [ PubMed ]
9. Goodman SN, Berlin JA. The use of predicted confidence intervals when planning experiments and the misuse of power when interpreting results. Ann Intern Med. 1994;121:200–206. [ DOI ] [ PubMed ]
10. Halpern SD, Karlawish JH, Berlin JA. The continuing unethical conduct of underpowered clinical trials. JAMA. 2002;288:358–362. [ DOI ] [ PubMed ]
11. Handl M, Drzik M, Cerulli G, Povysil C, Chlpik J, Varga F, Amler E, Trc T. Reconstruction of the anterior cruciate ligament: dynamic strain evaluation of the graft. Knee Surg Sports Traumatol Arthrosc. 2007;15:233–241. [ DOI ] [ PubMed ]
12. Harris WH. Traumatic arthritis of the hip after dislocation and acetabular fractures: treatment by mold arthroplasty: an end-result study using a new method of result evaluation. J Bone Joint Surg Am. 1969;51:737–755. [ PubMed ]
13. Hoenig JM, Heisey DM. The abuse of power: the pervasive fallacy of power calculations for data analysis. The American Statistician. 2001;55:19–24. [ DOI ]
14. Hsieh FY, Bloch DA, Larsen MD. A simple method of sample size calculation for linear and logistic regression. Stat Med. 1998;17:1623–1634. [ DOI ] [ PubMed ]
15. Jaeschke R, Singer J, Guyatt GH. Measurement of health status: ascertaining the minimal clinically important difference. Control Clin Trials. 1989;10:407–415. [ DOI ] [ PubMed ]
16. Jennison C, Turnbull BW. Group Sequential Methods with Applications to Clinical Trials. Boca Raton, FL: Chapman & Hall/CRC; 2000.
17. Kapoor B, Clement DJ, Kirkley A, Maffulli N. Current practice in the management of anterior cruciate ligament injuries in the United Kingdom. Br J Sports Med. 2004;38:542–544. [ DOI ] [ PMC free article ] [ PubMed ]
18. Kjaergard LL, Villumsen J, Gluud C. Reported methodologic quality and discrepancies between large and small randomized trials in meta-analyses. Ann Intern Med. 2001;135:982–989. [ DOI ] [ PubMed ]
19. Machin D, Campbell MJ. Statistical Tables for the Design of Clinical Trials. Oxford, UK: Blackwell Scientific Publications; 1987.
20. Marx RG, Jones EC, Angel M, Wickiewicz TL, Warren RF. Beliefs and attitudes of members of the American Academy of Orthopaedic Surgeons regarding the treatment of anterior cruciate ligament injury. Arthroscopy. 2003;19:762–770. [ DOI ] [ PubMed ]
21. Michener LA, McClure PW, Sennett BJ. American Shoulder and Elbow Surgeons Standardized Shoulder Assessment Form, patient self-report section: reliability, validity, and responsiveness. J Shoulder Elbow Surg. 2002;11:587–594. [ DOI ] [ PubMed ]
22. Mirza F, Mai DD, Kirkley A, Fowler PJ, Amendola A. Management of injuries to the anterior cruciate ligament: results of a survey of orthopaedic surgeons in Canada. Clin J Sport Med. 2000;10:85–88. [ DOI ] [ PubMed ]
23. Moher D, Pham B, Jones A, Cook DJ, Jadad AR, Moher M, Tugwell P, Klassen TP. Does quality of reports of randomised trials affect estimates of intervention efficacy reported in meta-analyses? Lancet. 1998;352:609–613. [ DOI ] [ PubMed ]
24. Pearson J, Neyman ES. On the use, interpretation of certain test criteria for purposes of statistical inference: Part I. Biometrika. 1928;20A:175–240.
25. Pearson ES, Neyman J. On the use, interpretation of certain test criteria for purposes of statistical inference: Part II. Biometrika. 1928;20A:263–294.
26. Rubinstein LV, Korn EL, Freidlin B, Hunsberger S, Ivy SP, Smith MA. Design issues of randomized phase II trials and a proposal for phase II screening trials. J Clin Oncol. 2005;23:7199–7206. [ DOI ] [ PubMed ]
27. Schulz KF, Chalmers I, Hayes RJ, Altman DG. Empirical evidence of bias: dimensions of methodological quality associated with estimates of treatment effects in controlled trials. JAMA. 1995;273:408–412. [ DOI ] [ PubMed ]
28. Stenning SP, Parmar MK. Designing randomised trials: both large and small trials are needed. Ann Oncol. 2002;13(suppl 4):131–138. [ DOI ] [ PubMed ]
29. Sterne JA, Davey Smith G. Sifting the evidence: what’s wrong with significance tests? BMJ. 2001;322:226–231. [ DOI ] [ PMC free article ] [ PubMed ]
30. Vaeth M, Skovlund E. A simple approach to power and sample size calculations in logistic regression and Cox regression models. Stat Med. 2004;23:1781–1792. [ DOI ] [ PubMed ]
View on publisher site
PDF (236.4 KB)
Collections

Add to Collections

How Many Participants for Quantitative Usability Studies: A Summary of Sample-Size Recommendations

July 25, 2021 2021-07-25

Email article
Share on LinkedIn
Share on Twitter

Where do these recommendations come from and how many participants do you really need? This is an important question. If you test with too few , your results may not be statistically reliable . If you test with too many, you’re essentially throwing your money away. We want to strike the perfect balance — collecting enough data points to be confident in our results, but not so many that we’re wasting precious research funding.

In most cases, we recommend 40 participants for quantitative studies. If you don’t really care about the reasoning behind that number, you can stop reading here. Read on if you do want to know where that number comes from, when to use a different number, and why you may have seen different recommendations.

Since this is a common confusion, let’s clarify: there are two kinds of studies, qualitative and quantitative. Qual aims at insights, not numbers , so statistical significance doesn’t come into play. In contrast, quant does focus on collecting UX metrics , so we need to ensure that these numbers are correct. And the key point: this article is about quant, not qual . ( Qualitative studies only need a small number of users , but that’s not what we’re discussing here.)

When we conduct quantitative usability studies, we’re collecting UX metrics — numbers that represent some aspect of the user experience.

For example, we might want to know what percentage of our users are able to book a hotel room on Expedia, a travel-booking site. We won’t be able to ask every Expedia user to try to book a hotel room. Instead, we will run a study in which will ask a subset of our target population of Expedia users to make a reservation.

Then, we’ll count how many participants in that study are able to complete the task and we’ll use that percentage to estimate the percentage of our population. Of course, what we get from the study is not going to be exactly the same as our population success rate (there is always going to be some amount of measurement error), but we hope that it will be close enough.

When the number of people we include in the study is small, the percentage from the study will be unlikely to predict the success rate of the whole population — that number will simply be too noisy.

As another example, image you want to figure out the average daily temperature in Berlin, Germany during the summer. You decide to estimate that average by looking only at three random daily temperatures. Those three days probably will not give you a very accurate number, will they? This is the problem with small samples for quantitative studies.

In a quantitative usability study, to get a reasonably trustworthy prediction for the behavior of your overall population, you need around 40 data points. There are nuances depending on how much risk you are willing to take and what exactly you are trying to measure.

The 40-participant recommendation comes from a calculation . That calculation estimates the minimum number of users needed to produce a reasonable prediction of your population behavior based on one study. It has specific assumptions, but it will work for many quantitative usability studies .

If you don’t care about statistics, you can stop reading at this point (or jump directly to the conclusion ). Otherwise, if you’re curious about the nuances behind this recommendation, keep reading.

In statistical terms, the 40-participant guideline comes from a very specific situation, which may or may not apply to your particular scenario. It assumes that you have a considerable user population (over 500 people) and that the following are true:

You want to estimate a binary metric such as success rate or conversion rate based on a study with a sample of your user population.
You aim for a 15% margin of error — namely, you want your true score (e.g., the success rate or conversion rate for your whole population) to be within 15% of the observed score (the percentage you obtained from your study).
You want to take very little risk of being wrong in this prediction (that is, you will use a confidence level of 95% for computing your margin of error).

If all the above are true, it turns out that you can calculate the number of participants you need for your study, and it is 39. We round it up to 40 — hence the above recommendation. (These estimates are often rounded up by a few participants. First, rounding up makes the numbers more memorable. Second, slight overrecruiting helps if something goes wrong with one or two participants and their data has to be removed. For example, you may discover during the study that you accidentally recruited an unrepresentative user or a cheater.)

It is possible to need fewer participants if the last two of the assumptions above are not true. Specifically, if you are:

Willing to have a margin of error that is bigger than 15%
Willing to take a larger risk

Willing to Have a Margin of Error Bigger than 15%

The margin of error tells you how much you can expect your overall population rate to vary as a function of the observed score. Any time you collect a metric you should compute a margin of error (or, equivalently, a confidence interval). In other words, if in your Expedia study, 70% of your study participants were able to book a room and your margin of error was 15%, it means that your whole-population completion rate (the true score) is 70% ± 15% — that is, it could be anywhere from 55% to 85%.

That range is 30% wide and it represents the precision of your estimate; it could, however, be the case that in some situations you don’t care if it’s a little wider and your margin of error is bigger (for example, if you want to be able to say that most people can use a certain feature of your UI). We don’t recommend going for margins of error bigger than 20% because your confidence interval for the true score will be quite wide and unlikely to be useful.

Willing to Take a Larger Risk

A 95% confidence level means that your margin of error computations will be wrong only 5% of the time. It is the gold standard for published academic research. However, most UX researchers work in applied research, not academic research. For practical purposes, you may be willing to take a little bit more risk.

(Taking more risk is cheaper and is a good idea if the risks of a somewhat unreliable result won’t be catastrophic. However, bear in mind that UX teams often use quantitative usability testing to inform prioritization and resource allocation, so unreliable data may be quite problematic.)

If you are willing to drop the confidence level to 90%, then a margin of error of 15% will require 28 users and a margin of error of 20% will require 15 users . Again, you may consider rounding these up for many good reasons (for example, you may end up having to remove some of your trials when you clean up the data). This is the origin of the 30-user guideline that you may have encountered elsewhere — that recommendation accepts more risk.

This table shows the number of participants needed for different confidence levels and desired margins of error for binary metrics. The lower the confidence level, the riskier the study. The bigger the margin of error, the lower your precision and the less useful the numbers will be.

If your metric is continuous or can be treated as continuous (e.g., task time, satisfaction or other types of rating, SUS score ), the formula for the number of participants will depend on an additional factor: the variability of your target population. (It will also depend, like for binary metrics, on the desired margin of error and the confidence level used). That is something that you could estimate separately for your population by running a pilot study.

Of course, a pilot study to estimate the standard deviation is quite expensive and it will itself involve a fairly large number of participants. On the other hand, in most quantitative usability studies, there are several metrics involved and usually at least one of them is binary. Therefore, we recommend using that binary metric as a constraint in deciding the number of users. In other words, if you are collecting success, task time, and satisfaction, then you can simply say I want a 15% margin of error for success at a 90% or 95% confidence level (and recruit 30 or 40 users respectively). That will usually result in good margins of error for the other metrics involved.

If, however, you collect only continuous metrics (this is unusual) and you cannot afford to estimate the standard deviation of your population, you must first settle on a desired value for your margin of error. Of course, your desired value will depend on what you are measuring and the range for a task. We usually recommend using as a desired value 15% or 20% of the mean — in other words, if your task time is around 1 minute, you would like a margin of error no bigger than 0.15–0.20 minutes (9 to 12 seconds); if your task time is around 10 minutes, your margin of error should be no bigger than 1.5–2 minutes.

Next, you can use Jakob Nielsen’s estimate of variability for website- and intranet-related continuous metrics . That estimate is 52% of the mean . In other words, if the mean task time is 1 min, your estimated standard deviation is 0.52 x 1 min = 0.52 minutes. If the mean task time is 10 minutes, then your estimated standard deviation will be 0.52 x 10 min = 5.2 minutes. With that supplementary assumption, you would need 47 users for a 15% margin of error at 95% confidence level, 33 users for a 15% margin of error at 90% confidence level, 26 users for a 20% margin of error at 95% confidence level and 19 users for a 20% margin of error at 90% confidence level. (Note that a 15% margin of error of 1 minute translates into 0.15 minutes — that is, 9 seconds.)

This table shows the required number of participants needed for a study involving continuous metrics such as time on task or satisfaction. Different numbers of participants are appropriate for different confidence levels and desired margins of error.

In general, the number of users can be determined using the following formula:

N is k squared times s squared divided by m squared.

The variables in that formula are:

K is a constant (1.96 for 95% confidence level or 1.645 for 90% confidence level)
s is your standard deviation as a proportion of the mean
m is your desired margin of error, also expressed as a proportion of the mean (0.15 corresponding to 15% or 0.20 corresponding to 20%)

If you estimate your standard deviation as a 52% (or 0.52) of the mean, then you can use the formula below:

N is k squared times 0.27 divided by m squared

Even though there are many different recommendations for sample sizes in quantitative usability testing, they are all consistent with each other — they simply make slightly different assumptions. We think the 40-user guideline is the simplest and the most likely to lead to good results — namely, a relatively small margin of error with a high confidence level.

However, you may settle for a lower number of users (around 30) if you want to take slightly more risk that your findings will not represent the behavior of your user population and thus decrease your confidence level to 90%. Moreover, if you also have tolerance for a larger margin of error, you can drop the number of users to 20 or even fewer, but that is generally a lot riskier.

An acceptable strategy (especially if you are on a tight budget and mostly interested in continuous metrics such as task time and satisfaction) is to start with as many users as you can comfortably afford — say, 20–25 users. Once you’ve collected your data from these users, calculate your margins of error and determine if they are tight enough for your purposes. If they are too wide, then consider adding more users. This approach, however, requires that you work fast: you’ll need to do your analysis in a matter of a few days in order to be able to run the extra participants very soon after the first batch. Otherwise, you risk compromising the validity of your study.

Choose the right sample size for your situation to ensure you’ll optimize your quantitative study: collecting just enough data, but not too much.

Jeff Sauro, James Lewis. 2016. Quantifying the User Experience: Practical Statistics for User Research . Elsevier.

Related Courses

Statistics for ux.

Calculate, interpret, and report the numbers from your quantitative UX studies

Measuring UX and ROI

Use metrics from quantitative research to demonstrate value

Remote User Research

Collect insights without leaving your desk

Learn More:

Why Use 40 Participants in Quantitative UX Research?

Page Laubheimer · 5 min

Coding in Thematic Analysis

Maria Rosala · 3 min

Practical vs. Statistical Significance

Caleb Sponheim · 3 min

Why You Cannot Trust Numbers from Qualitative Usability Studies

Raluca Budiu · 9 min

10 Survey Challenges and How to Avoid Them

Tanner Kohler · 15 min

Quantitative UX: Glossary

Raluca Budiu · 8 min

CASTLE Framework for Productivity/Workplace Applications

Page Laubheimer · 8 min

Confounding Variables in Quantitative Studies

Caleb Sponheim · 5 min

Should You Run a Survey?

Maddie Brown · 6 min

Root out friction in every digital experience, super-charge conversion rates, and optimize digital self-service

Uncover insights from any interaction, deliver AI-powered agent coaching, and reduce cost to serve

Increase revenue and loyalty with real-time insights and recommendations delivered to teams on the ground

Know how your people feel and empower managers to improve employee engagement, productivity, and retention

Take action in the moments that matter most along the employee journey and drive bottom line growth

Whatever they’re are saying, wherever they’re saying it, know exactly what’s going on with your people

Get faster, richer insights with qual and quant tools that make powerful market research available to everyone

Run concept tests, pricing studies, prototyping + more with fast, powerful studies designed by UX research experts

Track your brand performance 24/7 and act quickly to respond to opportunities and challenges in your market

Explore the platform powering Experience Management

Free Account
Product Demos
For Digital
For Customer Care
For Human Resources
For Researchers
Financial Services
All Industries

Popular Use Cases

Customer Experience
Employee Experience
Net Promoter Score
Voice of Customer
Customer Success Hub
Product Documentation
Training & Certification
XM Institute
Popular Resources
Customer Stories
Artificial Intelligence

Market Research

Partnerships
Marketplace

The annual gathering of the experience leaders at the world’s iconic brands building breakthrough business results, live in Salt Lake City.

English/AU & NZ
Español/Europa
Español/América Latina
Português Brasileiro
REQUEST DEMO

Sample size calculator

Updated December 8, 2023

Introduction to sample size

How can you calculate sample size, reduce the margin of error and produce surveys with statistically significant results? In this short guide, we explain how you can improve your surveys and showcase some of the tools and resources you can leverage in the process.

But first, when it comes to market research, how many people do you need to interview to get results representative of the target population with the level of confidence that you are willing to accept?

However, if all of this sounds new to you, let's start with what sample size is.

Free eBook: The complete guide to determining sample size

What is sample size?

Sample size is a term used in market research to define the number of subjects included in a survey, study, or experiment. In surveys with large populations, sample size is incredibly important. The reason for this is because it's unrealistic to get answers or results from everyone - instead, you can take a random sample of individuals that represent the population as a whole.

For example, we might want to compare the performance of long-distance runners that eat Weetabix for breakfast versus those who don't. Since it's impossible to track the dietary habits of every long-distance runner across the globe, we would have to focus on a segment of the survey population. This might mean selecting 1,000 runners for the study.

How can sample size influence results?

That said, no matter how diligent we are with our selection, there will always be some margin of error (also referred to as confidence interval) in the study results, that's because we can't speak to every long-distance runner or be confident of how Weetabix influences (in every possible scenario), the performance of long-distance runners. This is known as a "sampling error."

Larger sample sizes will help to mitigate the margin of error, helping to provide more statistically significant and meaningful results. In other words, a more accurate picture of how eating Weetabix can influence the performance of long-distance runners.

So what do you need to know when calculating the minimum sample size needed for a research project?

What you need to know to calculate survey sample size

Confidence interval (or margin of error).

The confidence interval is the plus-or-minus figure that represents the accuracy of the reported. Consider the following example:

A Canadian national sample showed "Who Canadians spend their money on for Mother's Day." Eighty-two percent of Canadians expect to buy gifts for their mom, compared to 20 percent for their wife and 15 percent for their mother-in-law. In terms of spending, Canadians expect to spend $93 on their wife this Mother's Day versus $58 on their mother. The national findings are accurate, plus or minus 2.75 percent, 19 times out of 20.

For example, if you use a confidence interval of 2.75 and 82% percent of your sample indicates they will "buy a gift for mom" you can be "confident (95% or 99%)" that if you had asked the question to ALL CANADIANS, somewhere between 79.25% (82%-2.75%) and 84.75% (82%+2.75%) would have picked that answer.

Confidence interval is also called the "margin of error." Are you needing to understand how the two calculations correlate?

Confidence level

The confidence level tells you how confident you are of this result. It is expressed as a percentage of times that different samples (if repeated samples were drawn) would produce this result. The 95% confidence level means that 19 times out of twenty that results would fall in this - + interval confidence interval. The 95% confidence level is the most commonly used.

When you put the confidence level and the confidence interval together, you can say that you are 95% (19 out of 20) sure that the true percentage of the population that will "buy a gift for mom" is between 79.25% and 84.75%.

Wider confidence intervals increase the certainty that the true answer is within the range specified. These wider confidence intervals come from smaller sample sizes. When the costs of an error is extremely high (a multi-million dollar decision is at stake) the confidence interval should be kept small. This can be done by increasing the sample size.

Population size

Population size is the total amount of people in the group you're trying to study. If you were taking a random sample of people across the U.K., then your population size would be just over 68 million (as of 09 August 2021).

Standard deviation

This refers to how much individual responses will vary between each other and the mean. If there's a low standard deviation, scores will be clustered near the mean with minimal variation. A higher standard deviation means that when plotted on a graph, responses will be more spread out.

Standard deviation is expressed as a decimal, and 0.5 is considered a "good" standard deviation to set to ensure a sample size that represents the population.

How can you calculate sample size?

After you've considered the four above variables, you should have everything required to calculate your sample size.

However, if you don't know your population size, you can still calculate your sample size. To do this, you need two pieces of information: a z-score and the sample size formula.

What is a z-score?

A z-score is simply the numerical representation of your desired confidence level. It tells you how many standard deviations from the mean your score is.

The most common percentages are 90%, 95%, and 99%.

z = (x – μ) / σ

As the formula shows, the z-score is simply the raw score minus the population mean and divided by the population's standard deviation.

Using a sample size calculation

Once you have your z-score, you can fill out your sample size formula, which is:

Is there an easier way to calculate sample size?

If you want an easier option, Qualtrics offers an online sample size calculator that can help you determine your ideal survey sample size in seconds. Just put in the confidence level, population size, margin of error, and the perfect sample size is calculated for you.

Best-practice tips for sample size

There are lots of variables to consider when it comes to generating a specific sample size. That said, there are a few best-practice tips (or rules) to ensure you get the best possible results:

1) Balance cost and confidence level

To increase confidence level or reduce the margin of error, you have to increase your sample size. Larger sizes almost invariably lead to higher costs. Take the time to consider what results you want from your surveys and what role it plays in your overall campaigns.

2) You don't always need statistically significant results

Depending on your target audience, you may not be able to get enough responses (or a large enough sample size) to achieve "statistically significant" results.

If it's for your own research and not a wider study, it might not be that much of a problem, but remember that any feedback you get from your surveys is important. It might not be statistically significant, but it can aid your activities going forward.

Ultimately, you should treat this on a case-by-case basis. Survey samples can still give you valuable answers without having sample sizes that represent the general population. But more on this in the section below.

3) Ask open-ended questions

Yes and no questions provide certainty, but open-ended questions provide insights you would have otherwise not received. To get the best results, it's worth having a mix of closed and open-ended questions. For a deeper dive into survey question types, check out our handbook.

Different types of surveys

From market research to customer satisfaction, there are plenty of different surveys that you can carry out to get the information you need, corresponding with your sample size.

The great thing about what we do at Qualtrics is that we offer a comprehensive collection of pre-made, customer, product, employee, and brand survey templates. This includes Net Promoter Score (NPS) surveys, manager feedback surveys, customer service surveys, and more.

The best part? You can access all of these templates for free. Each one is designed by our specialist team of subject matter experts and researchers so you can be sure that our best-practice question choices and clear designs will get more engagement and better quality data.

As well as offering free survey templates, you can check out our free survey builder. Trusted by over 11,000 brands and 99 of the top 100 business schools, our tool allows you to create, distribute and analyze surveys to find customer, employee, brand, product, and market research insights.

Drag-and-drop functionality means anyone can use it, and wherever you need to gather and analyze data, our platform can help.

Once you have determined your sample size , you’re ready for the next step in the research journey. market research.

Market research is the process of gathering information about consumers' needs and preferences, and it can provide incredible insights that help elevate your business (or your customers') to the next level.

If you want to learn more, we've got you covered. Just download our free guide and find out how you can:

Identify use cases for market research
Create and deliver effective market research campaigns
Take action on research findings

Qualtrics // Experience Management

Qualtrics, the leader and creator of the experience management category, is a cloud-native software platform that empowers organizations to deliver exceptional experiences and build deep relationships with their customers and employees.

With insights from Qualtrics, organizations can identify and resolve the greatest friction points in their business, retain and engage top talent, and bring the right products and services to market. Nearly 20,000 organizations around the world use Qualtrics’ advanced AI to listen, understand, and take action. Qualtrics uses its vast universe of experience data to form the largest database of human sentiment in the world. Qualtrics is co-headquartered in Provo, Utah and Seattle.

May 20, 2024

Best strategy & research books to read in 2024

May 13, 2024

Experience Management

X4 2024 Strategy & Research Showcase: Introducing the future of insights generation

November 7, 2023

Brand Experience

The 4 market research trends redefining insights in 2024

June 27, 2023

The fresh insights people: Scaling research at Woolworths Group

June 20, 2023

Bank less, delight more: How Bankwest built an engine room for customer obsession

April 1, 2023

Academic Experience

How to write great survey questions (with examples)

November 18, 2022

Statistical analysis software: your complete guide to getting started

November 4, 2022

Create online surveys with our free online survey maker tool

Stay up to date with the latest xm thought leadership, tips and news., request demo.

Ready to learn more about Qualtrics?

IMAGES

Sample size in quantitative research methods
PPT
What is a Sample Size: Examples, Formula
How to Determine Sample Size for a Research Study
PPT
Quantitative Research Size

VIDEO

Qualitative vs. Quantitative Research Methods #facts
Designing Large-Scale Quantitative Research Programs
Overview of Quantitative Research and Sample Quantitative Research Titles
Data Analysis in Stata
Difference between Qualitative and Quantitative Research
Sample Size

COMMENTS

Sample Size Justification
A good sample size justification in qualitative research is based on 1) an identification of the populations, including any sub-populations, 2) an estimate of the number of codes in the (sub-)population, 3) the probability a code is encountered in an information source, and 4) the sampling strategy that is used.
Sample size, power and effect size revisited: simplified and practical
In recent years, numerous software and websites have been developed which can successfully calculate sample size in various study types. Some of the important software and websites are listed in Table 2 and are evaluated based both on the remarks stated in the literature and on our own experience, with respect to the content, ease of use, and cost (31, 32).
Calculating the Sample Size in Quantitative Studies
Too large sample size is wastage of resources and use of too small sample size might fail to answer the research question or provide imprecise results and may question the validity of study.
The importance of large sample sizes in research
Charlesworth Author Services; 26 May, 2022; The importance of having Large Sample Sizes for your research. Sample size can be defined as the number of pieces of information, data points or patients (in medical studies) tested or enrolled in an experiment or study.On any hypothesis, scientific research is built upon determining the mean values of a given dataset.
When is enough, enough? Understanding and solving your sample size
The importance of an accurate sample size calculation when designing quantitative research is well ... there are additional factors to consider when determining sample size in health services research. Sample size requires deliberation from the outset of the study. ... Early identification of a sample size that is prohibitively large will ...
Large sample size, significance level, and the effect size: Solutions
If, however, the effect size is 0.15 with the same sample size (n = 46), the power of the test will decline significantly (see Fig. 1 b). Simply put, even when the impact of an independent variable is negligible, by using a large enough sample size, researchers can achieve enough power to reject H 0 in favor of the alternative hypothesis (H A).
How To Determine Sample Size for Quantitative Research
You need to determine how big of a sample size you need so that you can be sure the quantitative data you get from a survey is reflective of your target population as a whole - and so that the decisions you make based on the research have a firm foundation. Too big a sample and a project can be needlessly expensive and time-consuming.
Sample Size Essentials: The Foundation of Reliable Statistics
Statisticians have devised quantitative ways to find a good sample size. You want a large enough sample to have a reasonable chance of detecting a meaningful effect when it exists but not too large to be overly expensive. In general, these methods focus on using the population's variability. More variable populations require larger samples to ...
PDF Choosing the Size of the Sample
such as respondent-assisted sampling is not used, a large sample size may be required to obtain a sufficient sample size. Generally, the more rare and hidden the target population, the larger the required sample size. Ethical Considerations . Guideline 7.2. Ethical considerations. Taking the burden on study participants into consideration,
SampleSizePlanner: A Tool to Estimate and Justify Sample Size for Two
In a recent overview, Lakens (2021) listed six types of general approaches to justify sample size in quantitative empirical studies: (a) measure entire population, (b) resource constraints, (c) a priori power analysis, (d) accuracy, (e) heuristics, and (f) no justification. For the first approach, no quantitative justification is necessary, and ...
Sample size in quantitative research: Sample size will affect ...
That's your sample size--the number of participants needed to achieve valid conclusions or statistical significance in quantitative research. (Qualitative research requires a somewhat different approach. In this article, we'll answer these questions about sample size in quantitative research: Why does sample size matter?
Sample size: How many is enough?
This paper only examines sample size considerations in quantitative research. ... In addition, for a given effect size, alpha, and power, a larger sample size is required for a two-tailed test than for a one-tailed test. Different sample size formula are required depending on the research underlying statistical test, ...
Statistical Power, Sampling, and Effect Sizes: Three Keys to Research
The procedure requires the researcher to determine the needed sample size to attain the desired power to detect a predetermined ES. Figure 2 shows a graph of statistical power as a function of sample size. For 80% power (usually considered to be sufficient power), the group size required is about 50.
Sample Size and its Importance in Research
Sample Size and its Importance in Research. Chittaranjan Andrade. ABSTRACT. The sample size for a study needs to be estimated at the time the study is proposed; too large a sample is unnecessary and unethical, and too small a sample is unscientific and also unethical. The necessary sample size can be calculated, using statistical software ...
Statistics in Brief: The Importance of Sample Size in the Planning and
The graphs show the distribution of the test statistic (z-test) for the null hypothesis (plain line) and the alternative hypothesis (dotted line) for a sample size of (A) 32 patients per group, (B) 64 patients per group, and (C) 85 patients per group.For a difference in mean of 10, a standard deviation of 20, and a significance level α of 5%, the power (shaded area) increases from (A) 50%, to ...
Sample size determination: A practical guide for health researchers
Approaches to sample size calculation according to study design are presented with examples in health research. For sample size estimation, researchers need to (1) provide information regarding the statistical analysis to be applied, (2) determine acceptable precision levels, (3) decide on study power, (4) specify the confidence level, and (5 ...
How Many Participants for Quantitative Usability Studies: A Summary of
In a quantitative usability study, to get a reasonably trustworthy prediction for the behavior of your overall population, you need around 40 data points. There are nuances depending on how much risk you are willing to take and what exactly you are trying to measure. The 40-participant recommendation comes from a calculation.
Sample Size and its Importance in Research
Sample Size and its Importance in Research - Chittaranjan Andrade, 2020. Browse by discipline. Sage publishes a diverse portfolio of fully Open Access journals in a variety of disciplines. Alternatively, you can explore our Disciplines Hubs, including: Links to Books and Digital Library content from across Sage. Information for.
Sample size calculator
Sample size is a term used in market research to define the number of subjects included in a survey, study, or experiment. In surveys with large populations, sample size is incredibly important. The reason for this is because it's unrealistic to get answers or results from everyone - instead, you can take a random sample of individuals that ...

The importance of having Large Sample Sizes for your research

Defining ‘large sample size’ / ‘large study’ by topic

Statistical importance of having a large sample size

Fields that benefit most from large sample sizes

Importance of a larger sample size from a publishing perspective

Determining an adequate sample size

Ensuring you have an adequately large study

Share with your colleagues

Scientific Editing Services

When is enough, enough? Understanding and solving your sample size problems in health services research

Electronic supplementary material

A place to begin

Study design and hypothesis

Simulation and rules of thumb

Other considerations

Post hoc power analysis

Authors’ contributions

Acknowledgements

Authors’ information

Competing interests

Additional file

Contributor Information

Similar articles

Add to Collections

How To Determine Sample Size for Quantitative Research

Table of Contents:

Population size

Confidence interval (margin of error)

Confidence level

Standard deviation

Population variability

Project scope

Determining a good sample size for quantitative research

Get in touch to learn more about quantitative sample sizes!

Essential Brand Tracking Metrics

The Power of Shopper Insights

Wave 7 of quantilope's Direct-to-Consumer (DTC) Mattress Tracker

Sample size in quantitative research: Sample size will affect the significance of your research

Source Citation

Report an Issue

Statistics in Brief: The Importance of Sample Size in the Planning and Interpretation of Medical Research

Introduction

Desired Level of Significance

The Targeted Difference Between the Alternative Treatments

The Variability of the Data

Sample Size, Estimation, and Regression

Acknowledgments

Computation of Confidence Interval

Similar articles

Add to Collections

How Many Participants for Quantitative Usability Studies: A Summary of Sample-Size Recommendations

In This Article:

Willing to Have a Margin of Error Bigger than 15%

Willing to Take a Larger Risk

Related Courses

Measuring UX and ROI

Remote User Research

Related Topics

Learn More:

Related Articles:

Sample size calculator

Introduction to sample size

What is sample size?

How can sample size influence results?

What you need to know to calculate survey sample size

Confidence level

Population size

Standard deviation

How can you calculate sample size?

What is a z-score?

Using a sample size calculation

Is there an easier way to calculate sample size?

Best-practice tips for sample size

1) Balance cost and confidence level

2) You don't always need statistically significant results

3) Ask open-ended questions

Different types of surveys

Related Articles

Best strategy & research books to read in 2024

X4 2024 Strategy & Research Showcase: Introducing the future of insights generation