experimental demonstration of topological error correction

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings
My Bibliography
Collections
Citation manager

Save citation to file

Email citation, add to collections.

Create a new collection
Add to an existing collection

Add to My Bibliography

Your saved search, create a file for external citation management software, your rss feed.

Search in PubMed
Search in NLM Catalog
Add to Search

Experimental demonstration of topological error correction

Affiliation.

1 Shanghai Branch, National Laboratory for Physical Sciences at Microscale and Department of Modern Physics, University of Science and Technology of China, Shanghai 201315, China.
PMID: 22358838
DOI: 10.1038/nature10770

Scalable quantum computing can be achieved only if quantum bits are manipulated in a fault-tolerant fashion. Topological error correction--a method that combines topological quantum computation with quantum error correction--has the highest known tolerable error rate for a local architecture. The technique makes use of cluster states with topological properties and requires only nearest-neighbour interactions. Here we report the experimental demonstration of topological error correction with an eight-photon cluster state. We show that a correlation can be protected against a single error on any quantum bit. Also, when all quantum bits are simultaneously subjected to errors with equal probability, the effective error rate can be significantly reduced. Our work demonstrates the viability of topological error correction for fault-tolerant quantum information processing.

PubMed Disclaimer

Quantum computing: A topological route to error correction. Franson JD. Franson JD. Nature. 2012 Feb 22;482(7386):478-80. doi: 10.1038/482478a. Nature. 2012. PMID: 22358834 No abstract available.

Publication types

Search in MeSH

LinkOut - more resources

Full text sources.

Nature Publishing Group
Ovid Technologies, Inc.

Other Literature Sources

The Lens - Patent Citations

Molecular Biology Databases

Guide to Pharmacology

Citation Manager

NCBI Literature Resources

MeSH PMC Bookshelf Disclaimer

The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.

Experimental demonstration of topological error correction

Scalable quantum computing can only be achieved if qubits are manipulated fault-tolerantly. Topological error correction—a novel method which combines topological quantum computing and quantum error correction—possesses the highest known tolerable error rate for a local architecture. This scheme makes use of cluster states with topological properties and requires only nearest-neighbour interactions. Here we report the first experimental demonstration of topological error correction with an eight-photon cluster state. It is shown that a correlation can be protected against a single error on any qubit, and when all qubits are simultaneously subjected to errors with equal probability, the effective error rate can be significantly reduced. This demonstrates the viability of topological error correction. Our work represents the first experimental effort to achieve fault-tolerant quantum information processing by exploring the topological properties of quantum states.

Quantum computers exploit the laws of quantum mechanics, and can solve many problems exponentially more efficiently than their classical counterparts Shor94 ; Grover97Search ; Feynman82 . However, in the laboratory, the ubiquitous decoherence makes it notoriously hard to achieve the required high degree of quantum control. To overcome this problem, quantum error correction (QEC) has been invented Calderbank96 ; Steane96 ; Gottesman98 . The capstone result in QEC, the so-called threshold theorem Knill05 ; Aliferis06 , states that as long as the error rate p 𝑝 p per gate in a quantum computer is smaller than a threshold value p c subscript 𝑝 𝑐 p_{c} , arbitrarily long and accurate quantum computation is efficiently possible. Unfortunately, most methods of fault-tolerant quantum computing with high threshold ( 10 − 4 − 10 − 2 superscript 10 4 superscript 10 2 10^{-4}-10^{-2} ) require strong and long-range interactions Kitaev97 ; Knill05 ; Aliferis06 , and are thus difficult to implement. Local architectures are normally associated with much lower thresholds. For traditional concatenated codes on a 2D lattice of qubits with nearest-neighbour gates, the best threshold known to date Spedalieri09 is 2.02 × 10 − 5 2.02 superscript 10 5 2.02\times 10^{-5} .

In such lattices, it is advantageous to employ topological error correction (TEC) S ( 2 ); Raussendorf06 ; wang11 ; Raussendorf07 ; Barrett10 in the framework of topological cluster-state quantum computing. This scheme makes use of the topological properties in three-dimensional (3D) cluster states, which form an inherently error-robust “fabric” for computation. Local measurements drive the computation and, at the same time, implement the error correction. Active error correction and topological methods are combined, yielding a high error threshold Raussendorf06 ; wang11 of 0.7%–1.1% and tolerating loss rates Barrett10 up to 24.9%. This leaves room for the unavoidable imperfections of physical devices, and makes TEC close to the experimental state of the art. The 3D architecture can be further mapped onto a local setting in two spatial dimensions plus time Raussendorf07 , also with nearest-neighbour interactions only. Two detailed architectures have already been proposed Stock08 ; Devitt08 . Note that a distinct and also important topological scheme has been proposed, in which quantum computation is driven by non-abelian anyons Nayak08 ; Wilczek90 and fault tolerance is achieved via passive stabilization afforded by a ground-state energy gap.

Some simple QEC codes have been experimentally demonstrated in nuclear magnetic resonance Cory98 ; Knill01 , ion traps Chiaverini04 ; Schindler11 and optical systems Chaoyang08 ; Aoki09 . However, the experimental realization of topological QEC methods still remains a challenging task. The state-of-the-art technology for generating multipartite cluster state is up to six photons, while great endeavor is still underway to create non-ablelian anyons for the topological quantum computing Nayak08 ; Wilczek90 . Here, we develop an ultra-bright entangled-photon source by utilizing an interferometric Bell-type synthesizer. Together with a noise-reduction interferometer, we generate a polarization-encoded eight-photon cluster state, which is shown to possess the required topological properties for TEC. In accordance with the TEC scheme, we measure each photon (qubit) locally. Error syndromes are constructed from the measurement outcomes, and one topological quantum correlation is protected. We demonstrate: (1), if only one physical qubit suffers an error, the noisy qubit can be located and corrected, and (2), if all qubits are simultaneously subjected to errors with equal probability, the effective error rate is significantly reduced by error correction. Therefore, we have successfully carried out a proof-of-principle experiment that demonstrates the viability of Topological Error Correction —a central ingredient in topological cluster-state computing.

Cluster states and quantum computing

In cluster-state quantum computing Raussendorf01 , projective one-qubit measurements replace unitary evolution as the elementary process driving a quantum computation. The computation begins with a highly entangled multi-qubit state, the so-called cluster state | G ⟩ ket 𝐺 \left|G\right\rangle Schlingemann01 , which is specified by an interaction graph G 𝐺 G and can be created from a product state via the pairwise Ising interaction over the edges in G 𝐺 G . For each vertex i ∈ G 𝑖 𝐺 i\in G , one defines a stabilizer as K i : ≡ X i ⊗ e i j Z j K_{i}:\equiv X_{i}\mathop{\otimes}\limits_{e_{ij}}Z_{j} , where the product is over all the interaction edges e i j subscript 𝑒 𝑖 𝑗 e_{ij} connecting vertex i 𝑖 i to its neighbouring vertex j 𝑗 j . As usual, symbols X i subscript 𝑋 𝑖 X_{i} and Z j subscript 𝑍 𝑗 Z_{j} denote the bit- and phase-flip Pauli operators, respectively, acting on qubits i 𝑖 i and j 𝑗 j . State | G ⟩ ket 𝐺 \left|G\right\rangle is the unique joint eigenstate of a complete set of stabilizers K i subscript 𝐾 𝑖 K_{i} , K i | G ⟩ = | G ⟩ subscript 𝐾 𝑖 ket 𝐺 ket 𝐺 K_{i}\left|G\right\rangle=\left|G\right\rangle , for all the vertices i ∈ G 𝑖 𝐺 i\in G .

Cluster states in d ≥ 3 𝑑 3 d\geq 3 dimensions are resources for universal fault-tolerant quantum computing Raussendorf06 . Therein, the TEC capability—shared with Kitaev’s toric code Kitaev03 ; S ( 2 ) and the color code Bombin06 —is combined with the capability to process quantum information.

Topological error correction

1 +1 . Namely, any closed surface has the topological quantum correlation C F : ≡ ⟨ ⊗ f ∈ F X f ⟩ = 1 C_{F}:\equiv\left\langle\otimes_{f\in F}X_{f}\right\rangle=1 .

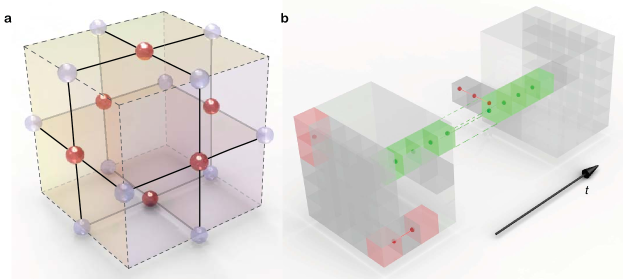
A larger cell complex is displayed in Fig. 1b, which encodes and propagates a logical qubit. It consists of 5 × 5 × T 5 5 𝑇 5\times 5\times T cells, with T 𝑇 T specifying a span of simulated time t 𝑡 t . A “defect” along the t 𝑡 t direction (shown as the line of green dots in Fig. 1b) is first carved out via performing local Z 𝑍 Z measurements. Then, the topological quantum correlation C F D = 1 subscript 𝐶 subscript 𝐹 𝐷 1 C_{F_{D}}=1 on a defect-enclosing closed surface, combined with the boundary, is used to encode a logical qubit. The evolution of the logical state from t 1 subscript 𝑡 1 t_{1} to t 2 subscript 𝑡 2 t_{2} is achieved by local X 𝑋 X measurements on all other physical qubits between t 1 subscript 𝑡 1 t_{1} and t 2 subscript 𝑡 2 t_{2} (see Ref. Fowler08 for the details). Quantum computing requires a much larger cell complex and more defects, where quantum algorithms are realized by appropriate braiding-like manipulation of defects (a sketch for the logical CNOT gate is shown in Appendix).

The quantum computation is possible precisely due to the topological quantum correlation C F D = 1 subscript 𝐶 subscript 𝐹 𝐷 1 C_{F_{D}}=1 on defect-enclosing closed surfaces F D subscript 𝐹 𝐷 F_{D} . The TEC capability arises from the Z 2 subscript Z 2 \textbf{Z}_{2} homology, a topological feature, of a sufficiently large 3D cell complex (see Appendix). For a given defect-enclosing closed surface F D subscript 𝐹 𝐷 F_{D} , there exist many homologically equivalent closed surfaces that represent the same topological correlation C F D = 1 subscript 𝐶 subscript 𝐹 𝐷 1 C_{F_{D}}=1 . This redundancy leads to the topological protection of the correlation Raussendorf06 .

Remarkably, in TEC it is sufficient to deal with Z 𝑍 Z errors, because an X 𝑋 X error has either no effect if immediately before X measurements or is equivalent to multiple Z 𝑍 Z errors. Finally, as a measurement-based quantum computation, corrections suggested by TEC are not applied to the remaining cluster state but rather to the classical outcomes of X 𝑋 X measurements.

Simpler topological cluster state

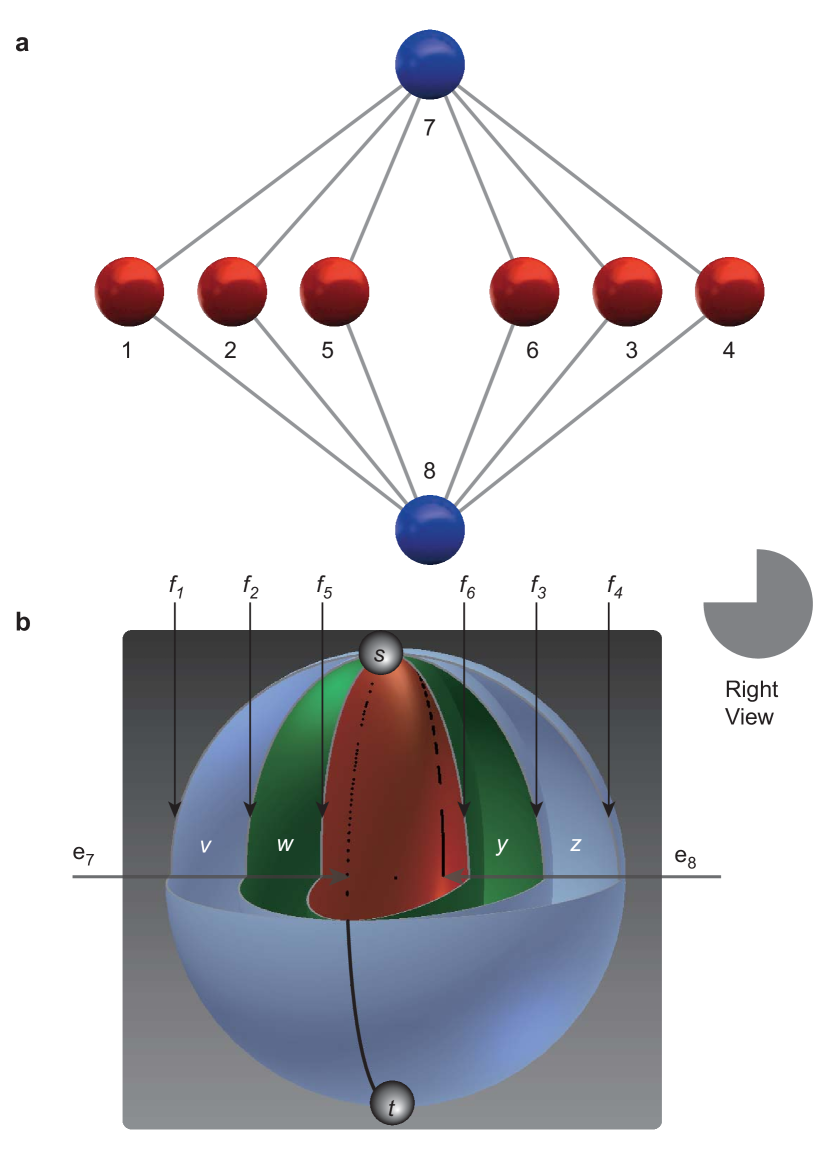
The cell complex in Fig. 1b encodes a propagating logical qubit via one topological correlation C F D = 1 subscript 𝐶 subscript 𝐹 𝐷 1 C_{F_{D}}=1 , and is robust against a local Z 𝑍 Z error. Unfortunately, it contains 180 physical qubits per layer, significantly beyond the reach of available techniques. We design a simpler graph state | G 8 ⟩ ket subscript 𝐺 8 \left|G_{8}\right\rangle , shown in Fig. 2a, to mimic the cell complex of Fig. 1b.

The topological feature of | G 8 ⟩ ket subscript 𝐺 8 \left|G_{8}\right\rangle can be seen via its association with the 3D cell complex in Fig. 2b, which consists of 4 elementary volumes { v , w , y , z } 𝑣 𝑤 𝑦 𝑧 \left\{v,w,y,z\right\} , 6 faces { f 1 , f 2 , f 3 , f 4 , f 5 , f 6 } subscript 𝑓 1 subscript 𝑓 2 subscript 𝑓 3 subscript 𝑓 4 subscript 𝑓 5 subscript 𝑓 6 \left\{f_{1},f_{2},f_{3},f_{4},f_{5},f_{6}\right\} , 2 edges { e 7 , e 8 } subscript 𝑒 7 subscript 𝑒 8 \{e_{7},e_{8}\} , and 2 vertices { s , t } 𝑠 𝑡 \left\{s,t\right\} . All 6 faces have the same boundary e 7 ∪ e 8 subscript 𝑒 7 subscript 𝑒 8 e_{7}\cup e_{8} , and any two of them forms a closed surface F 𝐹 F . The center volume is carved out, resembling the defect in Fig. 1b, and the to-be-protected topological correlation C F D subscript 𝐶 subscript 𝐹 𝐷 C_{F_{D}} reads

(1)

In this simple cell complex, the topological correlation C F D = 1 subscript 𝐶 subscript 𝐹 𝐷 1 C_{F_{D}}=1 is already multiply encoded, represented by any expectation ⟨ X i X j ⟩ delimited-⟨⟩ subscript 𝑋 𝑖 subscript 𝑋 𝑗 \langle X_{i}X_{j}\rangle with i ∈ { 1 , 2 , 5 } 𝑖 1 2 5 i\in\{1,2,5\} and j ∈ { 3 , 4 , 6 } 𝑗 3 4 6 j\in\{3,4,6\} . Moreover, there exist four other closed surfaces without enclosing the defect, corresponding to the boundary of volumes v 𝑣 v , w 𝑤 w , y 𝑦 y , z 𝑧 z , respectively. The “redundant” topological correlations are

(2)

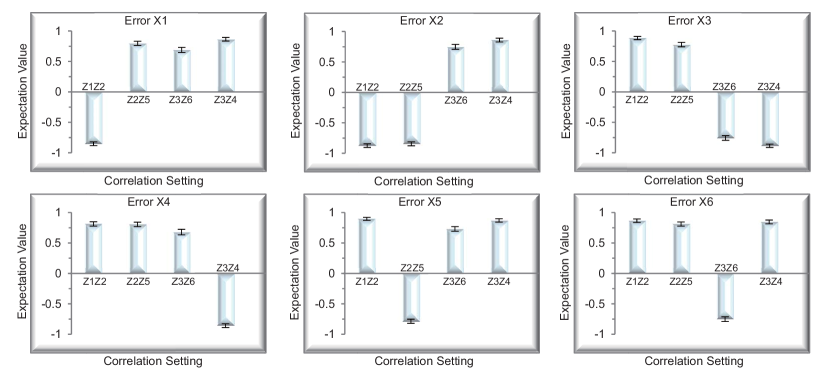
and can be used as error syndromes in TEC. As shown in Table 1, a single Z 𝑍 Z error on any physical qubit can be located and corrected.


1	-1	1	1	1
2	-1	-1	1	1
3	1	1	-1	-1
4	1	1	1	-1
5	1	-1	1	1
6	1	1	-1	1

Therefore, from the aspect of TEC capability, the cluster state | G 8 ⟩ ket subscript 𝐺 8 \left|G_{8}\right\rangle is analogous to the cell complex in Fig. 1b. They protect one topological correlation and are robust against a single Z 𝑍 Z error, albeit the cell complex in Fig. 2b is too small to propagate a logical qubit (see Appendix for detailed discussion).

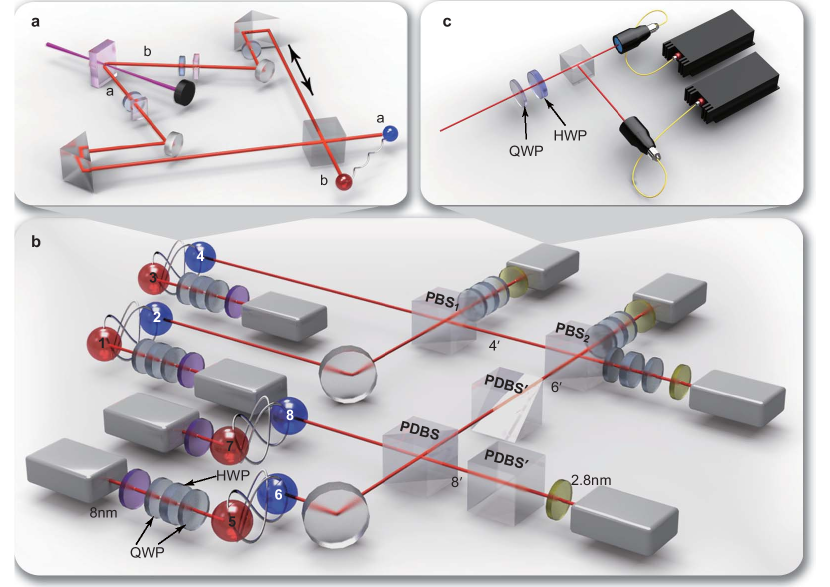
Preparation of the eight-photon cluster state

subscript ket 𝐻 𝐻 78 subscript ket 𝑉 𝑉 78 subscript ket 𝑉 𝑉 56 subscript ket 𝐻 𝐻 78 subscript ket 𝑉 𝑉 78 2 [|HH\rangle_{56}\left(|HH\rangle_{78}+|VV\rangle_{78}\right)+|VV\rangle_{56}\left(|HH\rangle_{78}-|VV\rangle_{78}\right)]/2 . Finally, photon 4’ and photon 6’ are superposed on PBS 2 . When eight photons come out of the output ports simultaneously, one obtains an entangled eight-photon cluster state:

(3)

This is exactly the cluster state | G 8 ⟩ ket subscript 𝐺 8 \left|G_{8}\right\rangle shown in Fig. 2a under Hadamard operations H ⊗ 8 superscript 𝐻 tensor-product absent 8 H^{\otimes 8} on all qubits. Note that the photons, which are interfered on the PBSs or at the PDBS, have the same bandwidth, and a star topology of the eight-photon interferometer leads to an effective noise-reduction.

ket |+\rangle/|-\rangle basis, where | ± ⟩ = 1 2 ( | H ⟩ ± | V ⟩ ) ket plus-or-minus 1 2 plus-or-minus ket 𝐻 ket 𝑉 |\pm\rangle=\frac{1}{\sqrt{2}}\left(|H\rangle\pm|V\rangle\right) . Fine adjustments of the delays between the different paths are tuned to ensure that all the photons arrive at the PBSs and PDBS simultaneously.

Measurement is taken for each individual photon by a polarization analyzer, which contains a combination of a QWP, a HWP and a PBS, together with two single-mode fibre-coupled single-photon detectors in each output of the PBS (see Fig. 3c). The complete set of the 256 possible combinations of eight-photon coincidence events is registered by a home-made FPGA-based programmable coincidence logic unit. We obtain an eight-fold coincidence rate of 3.2 per hour. Based on the measurements for the 256 possible polarization combinations in the | H ⟩ / | V ⟩ ket 𝐻 ket 𝑉 |H\rangle/|V\rangle basis (Fig. 4a), we obtain a signal-to-noise ratio of about 200:1, defined as the ratio of the average of the desired components to that of the non-desired ones. This indicates the success of preparing the desired eight-photon cluster state.

To more precisely characterize the cluster state, we use the entanglement-witness method to determine its fidelity. For this purpose, we construct a witness which allows for the lower bound on the state fidelity and requires only eight measurement settings (see Appendix):

					(4)

cos 𝑘 𝜋 6 X sin 𝑘 𝜋 6 Y \mbox{M}_{k}=\left[\mbox{cos}(\frac{k\pi}{6})\mbox{X}+\mbox{sin}(\frac{k\pi}{6})\mbox{Y}\right] . The results are shown in Fig. 4b, which yields the witness ⟨ W ⟩ = − 0.105 ± 0.023 delimited-⟨⟩ 𝑊 plus-or-minus 0.105 0.023 \langle W\rangle=-0.105\pm 0.023 , which is negative by 4.5 standard deviations. The state fidelity is F > 1 2 − ⟨ W ⟩ = 0.605 ± 0.023 𝐹 1 2 delimited-⟨⟩ 𝑊 plus-or-minus 0.605 0.023 F>\frac{1}{2}-\langle W\rangle=0.605\pm 0.023 . The presence of genuine eight-photon entanglement is confirmed.

Experimental topological error correction

Given such a cluster state, topological error correction is implemented using a series of single-qubit measurements and classical correction operations. In the laboratory, operations are performed on state ( 3 ), differing from | G 8 ⟩ ket subscript 𝐺 8 \left|G_{8}\right\rangle in Fig. 2a by Hadamard operation H ⊗ 8 superscript 𝐻 tensor-product absent 8 H^{\otimes 8} . Therefore, the to-be-protected correlation ⟨ X 5 X 6 ⟩ delimited-⟨⟩ subscript 𝑋 5 subscript 𝑋 6 \left\langle X_{5}X_{6}\right\rangle in Eq. ( 1 ) corresponds to ⟨ Z 5 Z 6 ⟩ delimited-⟨⟩ subscript 𝑍 5 subscript 𝑍 6 \left\langle Z_{5}Z_{6}\right\rangle in the experiment; the same applies to the syndrome correlations ( 2 ). Meanwhile, X 𝑋 X errors are engineered instead of Z 𝑍 Z errors.

In the experiment, the noisy quantum channels on polarization qubits are engineered by one HWP sandwiched with two QWPs, which are set at 90 degrees. By randomly setting the HWP axis to be oriented at ± θ plus-or-minus 𝜃 \pm\theta with respect to the horizontal direction, the noisy quantum channel can be engineered with a bit-flip error probability of p = sin 2 ( 2 θ ) 𝑝 superscript sin 2 2 𝜃 p=\mbox{sin}^{2}(2\theta) .

We first study the case that only a single X 𝑋 X error occurs on one of the six photons { 1 , ⋯ , 6 } 1 ⋯ 6 \{1,\cdots,6\} . The syndrome correlations are measured, and the results are shown in Fig. 5. For comparison, we also plot the correlations without any engineered error in Fig. 4c. Indeed, one can precisely locate the physical qubit undergoing an X 𝑋 X error.

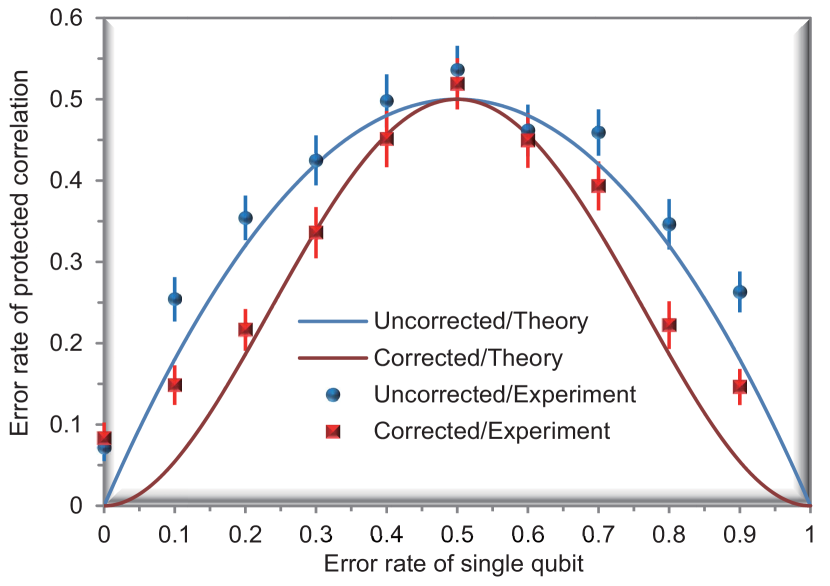
We then consider the case that all the six photons are simultaneously subject to a random X 𝑋 X error with equal probability 0 < p < 1 0 𝑝 1 0<p<1 , and study the rate of errors, ⟨ Z 5 Z 6 ⟩ = − 1 delimited-⟨⟩ subscript 𝑍 5 subscript 𝑍 6 1 \langle Z_{5}Z_{6}\rangle=-1 , for the topological quantum correlation ⟨ Z 5 Z 6 ⟩ delimited-⟨⟩ subscript 𝑍 5 subscript 𝑍 6 \langle Z_{5}Z_{6}\rangle . Without error correction, the error rate of correlation ⟨ Z 5 Z 6 ⟩ delimited-⟨⟩ subscript 𝑍 5 subscript 𝑍 6 \langle Z_{5}Z_{6}\rangle is P = 1 − ( 1 − p ) 2 − p 2 𝑃 1 superscript 1 𝑝 2 superscript 𝑝 2 P=1-(1-p)^{2}-p^{2} . With error correction, the residual error becomes

(5)

For small p 𝑝 p , the residual error rate after error correction is significantly reduced as compared to the unprotected case. As shown in Fig. 6, the experimental results are in good agreement with these theoretical predictions. Considerable improvement of the robustness of the ⟨ Z 5 Z 6 ⟩ delimited-⟨⟩ subscript 𝑍 5 subscript 𝑍 6 \langle Z_{5}Z_{6}\rangle correlation can be seen both in theory and in practice.

In the experiment, the whole measurement takes about 80 days. This requires an ultra stability of our setup. The imperfections in the experiment are mainly due to the undesired components in the | H ⟩ / | V ⟩ ket 𝐻 ket 𝑉 |H\rangle/|V\rangle basis, arising from higher-order emissions of entangled photons, and the imperfect photon overlapping at the PBSs and the PDBS. In spite of these imperfections, the viability of TEC is clearly demonstrated in the experiment.

In the current work, we have experimentally demonstrated TEC with an eight-photon cluster state. This state represents the current state-of-the-art for preparation of cluster states in any qubit system and is of particular interest in studying multipartite entanglement and quantum information processing. The scalable construction of cluster states in the future will require further development of high-efficiency entanglement sources and single-photon detectors Obrien07 . Recent results have shown that if the product of the number-resolving detector efficiency and the source efficiency is greater than 2/3, efficient linear optical quantum computation is possible Varnava08 . Solid technical progress towards this goal has been made such as deterministic storable single-photon sources Shuai06 and photon-number-resolving detectors Kardynal08 . This work represents the first experimental demonstration of TEC, an important step towards fault-tolerant quantum computation. In the scheme, given sufficient qubits and physical error rates below 0.7%–1.1%, arbitrary quantum computations could be performed arbitrarily reliably. The high threshold error rate is especially remarkable given that only nearest neighbour-interactions are required. Due to these advantages, TEC is especially well-suited for physical systems geometrically constrained to nearest-neighbour interactions, such as quantum dots Press08 , Josephson junction qubits Hime06 , ion traps Hensinger06 , cold atoms in optical lattices Jaksch99 and photonic modules Devitt08 . A quantum gate with an error rate below the threshold required in TEC is within reach of current experimental technology Benhelm08 . It would be interesting in future work to exploit cluster states of reachable size to implement topologically error-protected quantum algorithms by local measurements.

We acknowledge insightful discussions with M. A. Martin-Delgado, O. Gühne. We are grateful to X.-H. Bao for his original idea of the ultra-bright entanglement and to C.-Z. Peng for his idea of reducing high order emission. We would also like to thank C. Liu and S. Fölling for their help in designing the figures. This work has been supported by the NNSF of China, the CAS, the National Fundamental Research Program (under Grant No. 2011CB921300) and NSERC.

(1) Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science (1994).
(2) Grover, L. K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79 , 325 (1997).
(3) Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21 , 467–488 (1982).
(4) Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54 , 1098–1105 (1996).
(5) Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77 , 793–797 (1996).
(6) Gottesman, D. Theory of fault-tolerant quantum computation. Phys. Rev. A 57 , 127–137 (1998).
(7) Knill, E. Quantum computing with realistically noisy devices. Nature 434 , 39–44 (2005).
(8) Aliferis, P., Gottesman, D. & Preskill, J. Quantum accuracy threshold for concatenated distance-3 code. Quant. Inf. Comput. 6 , 97–165 (2006).
(9) Kitaev, A. Y. Quantum computations: Algorithms and error correction. Russ. Math. Surv. 52 , 1191–1249 (1997).
(10) Spedalieri, F. & Roychowdhury, V. P. Latency in local, two-dimensional, fault-tolerant quantum computing. Quant. Inf. Comput. 9 , 666–682 (2009).
(11) Dennis, E., Landahl, A., Kitaev, A. & Preskill, J. Topological quantum memory. J. Math. Phys. 43 , 4452–4505 (2002).
(12) Raussendorf, R., Harrington, J. & Goyal, K. A fault-tolerant one-way quantum computer. Ann. Phys. 321 , 2242–2270 (2006).
(13) Wang, D. S., Austin, A. G. & Hollenberg, L. C. L. Quantum computing with nearest neighbor interactions and error rates over 1%. Phys. Rev. A 83 , R020302 (2011).
(14) Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98 , 190504 (2007).
(15) Barrett, S. D. & Stace, T. M. Fault tolerant quantum computation with very high threshold for loss errors. Phys. Rev. Lett. 105 , 200502 (2010).
(16) Stock, R. & James, D. F. V. A scalable, high-speed measurement-based quantum computer using trapped ions. Phys. Rev. Lett. 102 , 170501 (2009).
(17) Devitt, S. J. et al. Topological cluster state computation with photons. New J. Phys. 11 , 083032 (2009).
(18) Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Sarma, S. D. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80 , 1083–1159 (2008).
(19) Wilczek, F. Fractional Statistics and Anyon Superconductivity (World Scientific, Singapore, 1990).
(20) Cory, D. G. et al. Experimental quantum error correction. Phys. Rev. Lett. 81 , 2152–2155 (1998).
(21) Knill, E., Laflamme, R., Martinez, R. & Negrevergne, C. Benchmarking quantum computers: The five-qubit error correcting code. Phys. Rev. Lett. 86 , 5811–5814 (2001).
(22) Chiaverini, J. et al. Realization of quantum error correction. Nature 432 , 602–605 (2004).
(23) Schindler, P. et al. Experimental repetitive quantum error correction. Science 332 , 1059–1061 (2011).
(24) Lu, C.-Y. et al. Experimental quantum coding against qubit loss error. Proc. Natl. Acad. Sci. USA 105 , 11050–11054 (2008).
(25) Aoki, T. et al. Quantum error correction beyond qubits. Nature Physics 5 , 541–546 (2009).
(26) Raussendorf, R. & Briegel, H. J. A one-way quantum computer. Phys. Rev. Lett. 86 , 5188–5191 (2001).
(27) Schlingemann, D. & Werner, R. F. Quantum error-correcting codes associated with graphs. Phys. Rev. A. 65 , 012308 (2001).
(28) Kitaev, A. Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 303 , 2–30 (2003).
(29) Bombin, H. & Martin-Delgado, M. A. Topological quantum distillation. Phys. Rev. Lett. 97 , 180501 (2006).
(30) Hatcher, A. Algebraic Topology. (Cambridge University Press, Cambridge, UK, 2002).
(31) Fowler, A. G. & Goyal, K. Topological cluster state quantum computing. Quant. Inf. Comput. 9 , 727–738 (2009).
(32) Yao, X.-C. et al. Observation of eight-photon entanglement. arXiv: 1105.6318v1 [quant–ph] (2011).
(33) Hofmann, H. F. & Takeuchi, S. Quantum phase gate for photonic qubits using only beam splitters and postselection. Phys. Rev. A 66 , 024308 (2002).
(34) Kiesel, N. et al. Experimental analysis of a four-qubit photon cluster state. Phys. Rev. Lett. 95 , 210502 (2005).
(35) O’Brien, J. L. Optical quantum computing. Science 318 , 1567–1570 (2007).
(36) Varnava, M., Browne, D. E. & Rudolph, T. How good must single photon sources and detectors be for efficient linear optical quantum computation? Phys. Rev. Lett. 100 , 060502 (2008).
(37) Chen, S. et al. Deterministic and storable single-photon source based on quantum memory. Phys. Rev. Lett. 97 , 173004 (2006).
(38) Kardynal, B. E., Yuan, Z. L. & Shields, A. J. An avalanche-photodiode-based photon-number-resolving detector. Nature Physics 2 , 425–428 (2008).
(39) Press, D. et al. Complete quantum control of a single quantum dot spin using ultrafast optical pulses. Nature 456 , 218–221 (2008).
(40) Hime, T. et al. Solid-state qubits with current-controlled coupling. Science 314 , 1427–1429 (2006).
(41) Hensinger, W. K. et al. T-junction ion trap array for two-dimensional ion shuttling, storage, and manipulation. Appl. Phys. Lett. 88 , 034101 (2006).
(42) Jaksch, D. et al. Entanglement of atoms via cold controlled collisions. Phys. Rev. Lett. 82 , 1975–1978 (1999).
(43) Benhelm, J., Kirchmair, G., Roos, C. F. & Blatt., R. Towards fault-tolerant quantum computing with trapped ions. Nature physics 4 , 463–466 (2008).

S.I Topological cluster state quantum computation

Cluster states and homology..

𝑉 F^{\prime}=F\pm\partial V .

𝑉 R(\partial V) can be used as error syndromes. We obtain one bit of such error syndrome per lattice cell; c.f. Fig. 1a.

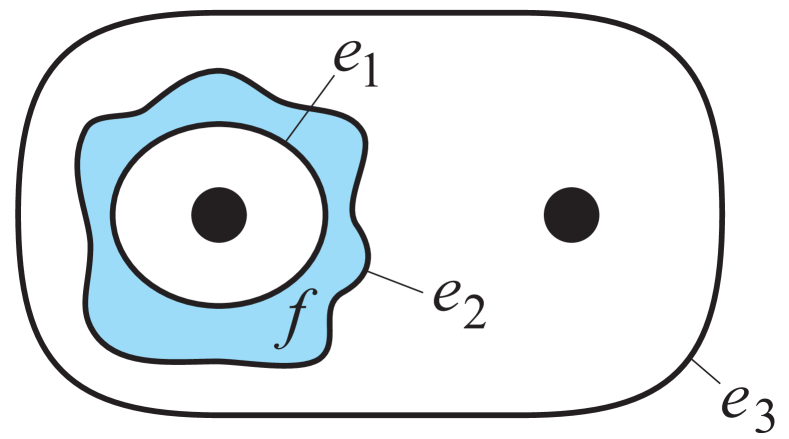
The errors have a geometrical interpretation, too. They correspond to 1-chains e 𝑒 e S ( 2 ) . Again, homology becomes relevant: Two homologically equivalent error chains e 𝑒 e and e ′ superscript 𝑒 ′ e^{\prime} have the same effect on computation.

In topological error correction with cluster states, the computational results and the syndromes are contained in correlations among outcomes of local X 𝑋 X -measurements. Detecting and correcting only phase flips of physical qubits is thus sufficient to correct arbitrary errors. Nevertheless, both bit flip and phase flip errors are present at the level of logical operations. The qubits in a 3D cluster state live on the faces and edges of the associated lattice. Logical phase errors are caused by erroneous measurement of face qubits, and logical spin flip errors are by erroneous measurement of edge qubits. For example, the 8-qubit cluster state | G 8 ⟩ ket subscript 𝐺 8 |G_{8}\rangle considered in this experiment has the correlation ⟨ G 8 | X 2 ⊗ X 2 ′ | G 8 ⟩ = 1 quantum-operator-product subscript 𝐺 8 tensor-product subscript 𝑋 2 subscript 𝑋 superscript 2 ′ subscript 𝐺 8 1 \langle G_{8}|X_{2}\otimes X_{2^{\prime}}|G_{8}\rangle=1 , in addition to the four correlations used as error syndromes for face qubits. It can be derived from a dual complex S ( 1 ) , and provides one bit of (dual) syndrome for the edge qubits of ℒ 8 subscript ℒ 8 {\cal{L}}_{8} .

Topologically protected quantum gates.

Topologically protected quantum gates are performed by measuring certain regions of qubits in the Z 𝑍 Z basis, which effectively removes them. The remaining cluster, whose qubits are to be measured in the X 𝑋 X and X ± Y plus-or-minus 𝑋 𝑌 X\pm Y basis, thereby attains a non-trivial topology in which fault-tolerant quantum gates can be encoded. Fig. S2 shows a macroscopic view of a 3D sub-cluster for the realization of a topologically protected CNOT gate S ( 3 , 4 ) . Only the topology of the cluster matters, individual lattice cells are not resolved. The cluster qubits in the line-like regions D 𝐷 D are measured in the Z 𝑍 Z -basis, the remaining cluster qubits in the X 𝑋 X -basis.

The fault-tolerance of measurement-based quantum computation with a 3D cluster state can be understood by mapping it to a Kitaev surface code propagating in time S ( 3 ) . In this picture, a 3D cluster state consists of many linked toric code surfaces plus extra qubits for code stabilizer measurement, entangled with these surfaces. The local measurements in each slice have the effect of teleporting the encoded state to the subsequent code surface. The code surfaces can support many encoded qubits because they have boundary. Encoded gates are implemented by changing the boundary conditions with time. This process is illustrated in Fig. S2 for the CNOT gate. Pieces of boundary in the code surface are created by the intersection of the line-like regions D 𝐷 D with surfaces of “constant time”. The 1-chains displayed in red represent encoded Pauli operators X ¯ ¯ 𝑋 \overline{X} at a given instant of simulated time. When propagating forward, an initial operator X ¯ c subscript ¯ 𝑋 𝑐 \overline{X}_{c} is converted into X ¯ c ⊗ X ¯ t tensor-product subscript ¯ 𝑋 𝑐 subscript ¯ 𝑋 𝑡 \overline{X}_{c}\otimes\overline{X}_{t} as required by conjugation under CNOT.

S.II Characterization of the 8-qubit cluster state

In order to characterize the generated 8-qubit cluster state, we use entanglement witnesses to verify its genuine multipartite entanglement S ( 8 ) . If 𝒲 𝒲 \mathcal{W} is an observable which has a positive expectation value on all biseparable states and a negative expectation value on the generated entangled state, we call this observable an entanglement witness. With the method introduced in Ref. S ( 9 ) , the witness is constructed as

(S.1)

is an orthogonal state of | ψ ⟩ ket 𝜓 |\psi\rangle , that is ⟨ ψ | ψ ′ ⟩ = 0 inner-product 𝜓 superscript 𝜓 ′ 0 \langle\psi|\psi^{\prime}\rangle=0 .

Then the witness is decomposed into a number of local von Neumann (or projective) measurements:

					(S.2)

cos 𝑘 𝜋 6 X sin 𝑘 𝜋 6 Y \mbox{M}_{k}=\left[\mbox{cos}(\frac{k\pi}{6})\mbox{X}+\mbox{sin}(\frac{k\pi}{6})\mbox{Y}\right] . The experimental results are shown in Fig. 4b in the main text, which yields the witness ⟨ W ⟩ = − 0.105 ± 0.023 delimited-⟨⟩ 𝑊 plus-or-minus 0.105 0.023 \langle W\rangle=-0.105\pm 0.023 , which is negative by 4.5 standard deviations.

S (1) Raussendorf, R., Harrington, J., Goyal, K. A fault-tolerant one-way quantum computer. Ann. Phys. 321, 2242-2270 (2006).
S (2) Dennis, E., Landahl, A., Kitaev, A. & Preskill, J. Topological quantum memory. J. Math. Phys. 43 , 4452 4505 (2002).
S (3) Raussendorf, R., Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504 (2007).
S (4) Raussendorf, R., Harrington, J., Goyal, K. Topological fault-tolerance in cluster state quantum computation. New J. Phys. 9 , 199 (2007).
S (5) Raussendorf, R., Bravyi, S. & Harrington, J. Long-range quantum entanglement in noisy cluster states, Phys. Rev. A 71 062313 (2005).
S (6) Fowler, A. G., Goyal, K. Topological cluster state quantum computing. Preprint at ⟨ ⟨ \langle http://arxiv.org/abs/0805.3202 ⟩ ⟩ \rangle (2008).
S (7) Fowler, A. G., Stephens, A. M., Groszkowski, P. High threshold universal quantum computation on the surface code . Preprint at ⟨ ⟨ \langle http://arxiv.org/abs/0803.0272 ⟩ ⟩ \rangle (2008).
S (8) Bourennane, M., Eibl, M., Kurtsiefer, C., et al. Experimental detection of multipartite entanglement using witness operators. Phys. Rev. Lett. 92, 087902 (2004).
S (9) Gühne, O., Lu, C. Y., Gao, W. B., Pan, J. W. Toolbox for entanglement detection and fidelity estimation. Phys. Rev. A 76, 030305 (2007).

Europe PMC requires Javascript to function effectively.

Either your web browser doesn't support Javascript or it is currently turned off. In the latter case, please turn on Javascript support in your web browser and reload this page.

Corpus ID: 260437837

Experimental demonstration of topological error correction

Wei-bo Gao , A. Fowler , +8 authors J. Pan
Published 11 May 2009

Figures and Tables from this paper

One Citation

Quantum interferometry with three-dimensional geometry, 9 references, related papers.

Showing 1 through 3 of 0 Related Papers

Experimental demonstration of topological error correction

Yao, Xing-Can
Wang, Tian-Xiong
Chen, Hao-Ze
Gao, Wei-Bo
Fowler, Austin G.
Raussendorf, Robert
Chen, Zeng-Bing
Liu, Nai-Le
Lu, Chao-Yang
Deng, You-Jin
Chen, Yu-Ao
Pan, Jian-Wei

Quantum Physics

Browse Econ Literature

Working papers
Software components
Book chapters
JEL classification

More features

Subscribe to new research

RePEc Biblio

Author registration.

Economics Virtual Seminar Calendar NEW!

Experimental demonstration of topological error correction

Author & abstract
1 Citations
Related works & more

Corrections

(Shanghai Branch, University of Science and Technology of China)

(CQC2T, School of Physics, University of Melbourne)

(University of British Columbia, Vancouver, British Columbia V6T 1Z1, Canada)

Suggested Citation

Download full text from publisher.

Follow serials, authors, keywords & more

Public profiles for Economics researchers

Various research rankings in Economics

RePEc Genealogy

Who was a student of whom, using RePEc

Curated articles & papers on economics topics

Upload your paper to be listed on RePEc and IDEAS

New papers by email

Subscribe to new additions to RePEc

EconAcademics

Blog aggregator for economics research

Cases of plagiarism in Economics

About RePEc

Initiative for open bibliographies in Economics

News about RePEc

Questions about IDEAS and RePEc

RePEc volunteers

Participating archives

Publishers indexing in RePEc

Privacy statement

Found an error or omission?

Opportunities to help RePEc

Get papers listed

Have your research listed on RePEc

Open a RePEc archive

Have your institution's/publisher's output listed on RePEc

Get RePEc data

Use data assembled by RePEc

We’re fighting to restore access to 500,000+ books in court this week. Join us!

Internet Archive Audio

experimental demonstration of topological error correction

This Just In
Grateful Dead
Old Time Radio
78 RPMs and Cylinder Recordings
Audio Books & Poetry
Computers, Technology and Science
Music, Arts & Culture
News & Public Affairs
Spirituality & Religion
Radio News Archive

Flickr Commons
Occupy Wall Street Flickr
NASA Images
Solar System Collection
Ames Research Center

All Software
Old School Emulation
MS-DOS Games
Historical Software
Classic PC Games
Software Library
Kodi Archive and Support File
Vintage Software
CD-ROM Software
CD-ROM Software Library
Software Sites
Tucows Software Library
Shareware CD-ROMs
Software Capsules Compilation
CD-ROM Images
ZX Spectrum
DOOM Level CD

Smithsonian Libraries
FEDLINK (US)
Lincoln Collection
American Libraries
Canadian Libraries
Universal Library
Project Gutenberg
Children's Library
Biodiversity Heritage Library
Books by Language
Additional Collections

Prelinger Archives
Democracy Now!
Occupy Wall Street
TV NSA Clip Library
Animation & Cartoons
Arts & Music
Computers & Technology
Cultural & Academic Films
Ephemeral Films
Sports Videos
Videogame Videos
Youth Media

Search the history of over 866 billion web pages on the Internet.

Mobile Apps

Wayback Machine (iOS)
Wayback Machine (Android)

Browser Extensions

Archive-it subscription.

Explore the Collections
Build Collections

Save Page Now

Capture a web page as it appears now for use as a trusted citation in the future.

Please enter a valid web address

Donate Donate icon An illustration of a heart shape

Experimental demonstration of topological error correction

Bookreader item preview, share or embed this item, flag this item for.

Graphic Violence
Explicit Sexual Content
Hate Speech
Misinformation/Disinformation
Marketing/Phishing/Advertising
Misleading/Inaccurate/Missing Metadata

plus-circle Add Review comment Reviews

Download options.

For users with print-disabilities

IN COLLECTIONS

Uploaded by jakej on September 21, 2013

Experimental demonstration of topological error correction

2012, Nature

Related Papers

Physical Review Letters

Yong Siah Teo

New Journal of Physics

Austin Fowler

Keisuke Fujii

Markus Hennrich

A novel scheme is presented for fault-tolerant quantum computation based on the cluster model. Some relevant logical cluster states are constructed in concatenation by post-selection through verification, without necessity of recovery operation, where a suitable code such as the Steane's 7-qubit code is adopted for transversal operations. This simple concatenated construction of verified cluster states achieves a high noise threshold ~4%, and restrains the divergence of resources.

Physical Review A

Loading Preview

Sorry, preview is currently unavailable. You can download the paper by clicking the button above.

RELATED PAPERS

David Simon

Austin Fowler , Adam Paetznick

Peter P Rohde

Pejman Jouzdani

Krysta Svore , Barbara Terhal

IEEE Transactions On Nanotechnology

Vwani Roychowdhury

Nature Communications

David Abraham

Nature Physics

Jacob Taylor

Rainer Kaltenbaek , G. Weihs

arXiv (Cornell University)

Morteza Saheb Zamani

Masoud Mohseni

George Rajna

npj Quantum Information

Joaquin Garcia-Alfaro

Michel Dyakonov

K. Birgitta WHALEY

Peter Van Loock , Samuel Braunstein

Steven Simon

EPJ Quantum Technology

David DiVincenzo

Mauro Paternostro

Steven Duplij

Article Contents

Introduction, experimental setup, data availability, acknowledgements, author contributions.

< Previous

Experimental exploration of five-qubit quantum error-correcting code with superconducting qubits

Ming Gong and Xiao Yuan are equally contributed to this work.

Article contents
Figures & tables
Supplementary Data

Ming Gong, Xiao Yuan, Shiyu Wang, Yulin Wu, Youwei Zhao, Chen Zha, Shaowei Li, Zhen Zhang, Qi Zhao, Yunchao Liu, Futian Liang, Jin Lin, Yu Xu, Hui Deng, Hao Rong, He Lu, Simon C Benjamin, Cheng-Zhi Peng, Xiongfeng Ma, Yu-Ao Chen, Xiaobo Zhu, Jian-Wei Pan, Experimental exploration of five-qubit quantum error-correcting code with superconducting qubits, National Science Review , Volume 9, Issue 1, January 2022, nwab011, https://doi.org/10.1093/nsr/nwab011

Permissions Icon Permissions

Quantum error correction is an essential ingredient for universal quantum computing. Despite tremendous experimental efforts in the study of quantum error correction, to date, there has been no demonstration in the realisation of universal quantum error-correcting code, with the subsequent verification of all key features including the identification of an arbitrary physical error, the capability for transversal manipulation of the logical state and state decoding. To address this challenge, we experimentally realise the [5, 1, 3] code, the so-called smallest perfect code that permits corrections of generic single-qubit errors. In the experiment, having optimised the encoding circuit, we employ an array of superconducting qubits to realise the [5, 1, 3] code for several typical logical states including the magic state, an indispensable resource for realising non-Clifford gates. The encoded states are prepared with an average fidelity of |$57.1(3)\%$| while with a high fidelity of |$98.6(1)\%$| in the code space. Then, the arbitrary single-qubit errors introduced manually are identified by measuring the stabilisers. We further implement logical Pauli operations with a fidelity of |$97.2(2)\%$| within the code space. Finally, we realise the decoding circuit and recover the input state with an overall fidelity of |$74.5(6)\%$|⁠ , in total with 92 gates. Our work demonstrates each key aspect of the [5, 1, 3] code and verifies the viability of experimental realisation of quantum error-correcting codes with superconducting qubits.

Quantum computers can tackle classically intractable problems [ 1 ] and efficiently simulate many-body quantum systems [ 2 ]. However, quantum computers are notoriously difficult to control, due to their ubiquitous yet inevitable interaction with their environment, together with imperfect manipulations that constitute the algorithm. The theory of fault tolerance has been developed as the long-term solution to this issue, enabling universal error-free quantum computing with noisy quantum hardware [ 3–7 ]. The logical qubits of an algorithm can be represented using a larger number of flawed physical qubits. Providing that the machine is sufficiently large (high qubit count), and that physical errors happen with a probability below a certain threshold, then such errors can be systematically detected and corrected [ 8 , 9 ]. In experiment, several small quantum error-correcting codes (QECCs), including the repetition code [ 10–16 ], the four-qubit error-detecting code [ 17–19 ], the seven-qubit color code [ 20 ], the bosonic quantum error-correcting code [ 21 , 22 ] and others [ 23–26 ], have been realised with different hardware platforms. These works have shown the success of realising error-correcting codes with non-destructive stabiliser measurements and their application in extending the system lifetime [ 19 , 25 ]. Nevertheless, previous experiments are limited to restricted codes for correcting certain types of errors or the preparation of specific logical states. It remains an open challenge to realise a fully-functional QECC.

Here, we focus on the five-qubit [5, 1, 3] code, the ‘perfect’ code that can protect a logical qubit from an arbitrary single physical error using the smallest number of qubits [ 6 , 7 ]. While proof-of-principle experimental demonstrations of the [5, 1, 3] code have been conducted on NMR systems [ 27 ], whether it could be incorporated in more scalable quantum computing systems and protect errors presented in these systems remain open. Here, we focus on the realisation of the five-qubit code with superconducting qubit systems. As a preparatory theoretical step, we recompile the universal encoding circuit that prepares an arbitrary logical state in order to realise it with the fewest possible number of nearest-neighbour two-qubit gates. In experiment, we implement basic functions of the code by realising logical state preparation, transversal logical operations and state decoding.

The five-qubit code has distance three and therefore all single-qubit errors can be identified (and thus corrected) while all double-qubit errors can be detected. When there is no error, all stabiliser measurements should yield +1 for the encoded state |$\mathinner {|{\Psi }\rangle }_L$|⁠ . When an error happens, one or more stabiliser measurements may yield −1. As there are four stabilisers whose measurement may take either +1 or −1 values, there are in total 15 syndrome measurement results with at least one outcome being −1. If we consider the ways in which a single Pauli error can afflict one of the five qubits, we note that there are 15 possibilities (three error types and five locations), with each mapping to a specific one of the 15 syndromes. When a two-qubit error happens, we again find that at least one of the stabiliser measurements takes −1. This heralds the fact that some error has occurred. However, since different double-qubit errors may have the same syndrome, we can only detect double-qubit errors without the capability of identifying or correcting them. Nevertheless, this latter property can be useful in some situations, such as state preparation, where we can simply discard a faulty realisation and restart.

Without using ancillary qubits, the original circuit for encoding the logical state |$\mathinner {|{\Psi }\rangle }_L$| requires a number of two-qubit gates that are non-local with respect to a linear architecture [ 6 , 7 ]. To tailor the circuit for superconducting systems that only involve nearest-neighbour controlled-phase gates, we recompile the encoding circuit to have the minimal possible number (eight) of nearest-neighbour control-phase gates as shown in Fig. 1 (a). We provide the details of circuit compilation in the online supplementary material.

$(a) Encoding quantum circuit of the five-qubit code. Here, the qubit labels Q1 ∼ Q5 are arranged to correspond with Equation (1); G1 and G2 are single-qubit gates to prepare the input state $a\mathinner {|{0}\rangle }+b\mathinner {|{1}\rangle }$ for encoding; Yα and Zα are the rotation gates around the Y and Z axes for an angle απ, respectively. In total, there are 27 layers of gate operations, including 54 single-qubit gates and eight nearest-neighbour controlled-phase gates. The single-qubit gates on different qubits can be applied in parallel, while the two-qubit gates can only be applied individually owing to the Z crosstalk. (b) Expectation values of 31 stabilisers for the encoded logical state $\mathinner {|{T}\rangle }_L$. Error bars representing a 95% confidence interval are estimated via bootstrapping. (c) Expectation values of logical Pauli operators and state fidelity of the encoded magic state.$

(a) Encoding quantum circuit of the five-qubit code. Here, the qubit labels Q 1 ∼ Q 5 are arranged to correspond with Equation ( 1 ); G 1 and G 2 are single-qubit gates to prepare the input state |$a\mathinner {|{0}\rangle }+b\mathinner {|{1}\rangle }$| for encoding; Y α and Z α are the rotation gates around the Y and Z axes for an angle απ, respectively. In total, there are 27 layers of gate operations, including 54 single-qubit gates and eight nearest-neighbour controlled-phase gates. The single-qubit gates on different qubits can be applied in parallel, while the two-qubit gates can only be applied individually owing to the Z crosstalk. (b) Expectation values of 31 stabilisers for the encoded logical state |$\mathinner {|{T}\rangle }_L$|⁠ . Error bars representing a 95% confidence interval are estimated via bootstrapping. (c) Expectation values of logical Pauli operators and state fidelity of the encoded magic state.

The device for the implementation of the five-qubit error-correcting code is a 12-qubit superconducting quantum processor [ 28 ]. Among these 12 qubits, we chose five adjacent qubits to perform the experiment. The qubits are capacitively coupled to their nearest neighbours. The capacitively coupled XY control lines enable the application of single-qubit rotation gates by applying microwave pulses, and the inductively coupled Z control lines enable the double-qubit controlled-phase gates by adiabatically tuning the two-qubit state |$\mathinner {|{11}\rangle }$| close to the avoid level crossing of |$\mathinner {|{11}\rangle }$| and |$\mathinner {|{02}\rangle }$| [ 28 ]. After careful calibrations and gate optimisations, we have the average gate fidelities as high as 0.9993 for single-qubit gates and 0.986 for two-qubit gates. With the implementation of only single-qubit rotation gates and double-qubit controlled-phase gates, we realised the circuit for encoding and decoding of the logical state. More details about the experimental setup are given in the online supplementary material.

On a superconducting quantum processor [ 28 ], we experimentally realised the logical states |$\mathinner {|{0}\rangle }_L$|⁠ , |$\mathinner {|{1}\rangle }_L$|⁠ , |$\mathinner {|{\pm }\rangle }_L$| and |$\mathinner {|{\pm i}\rangle }_L$| that are eigenstates of the logical Pauli operators X L , Y L , Z L and the magic state |$\mathinner {|{T}\rangle }_L= (\mathinner {|{0}\rangle }_L+e^{i\pi /4}\mathinner {|{1}\rangle }_L)/\sqrt{2}$| that cannot be realised by applying Clifford operations on any eigenstate of the logical Pauli operators. The expectation values of the stabiliser operators of |$\mathinner {|{T}\rangle }_L$| are shown in Fig. 1 (b). The fidelity between the experimentally prepared state and the ideal state |$\mathinner {|{\Psi }\rangle }_L\mathinner {\langle {\Psi }|}_L$| is determined by the measurement of the 32 stabiliser operators in |$\prod _{i=1}^5(g_0+g_i)$|⁠ . We omit the g 0 one as it is constantly 1. In this way, we obtained the state fidelity as the average of the 32 stabilisers by picking up corresponding measurement results among the state tomography results. Finally, the state fidelity of |$\mathinner {|{T}\rangle }_L$| reaches 54.5(4)%. The fidelities of other prepared states are shown in the online supplementary material, with an average fidelity of |$57.1(3)\%$|⁠ . The main error in preparing the encoded state is from decoherence, especially the relatively short dephasing time. In a numerical simulation of the experiment with decoherence (see the online supplementary material for details), the state fidelity of |$\mathinner {|{T}\rangle }_L$| is |$58.9\%$|⁠ . After numerically increasing the dephasing time to be the same as the energy relaxation time, the state fidelity can be increased to |$92.1\%$|⁠ , indicating a potential direction for future improvements.

Given the realisation of the logical state, one can proceed to verification of the error correction/detection ability of the five-qubit code. Acting on the logical encoded state |$\mathinner {|{T}\rangle }_L$|⁠ , we systematically introduce every type of single-qubit error by artificially applying the corresponding single-qubit gate on one of the five qubits. Then, by measuring the four stabilisers g 1 , g 2 , g 3 and g 4 , we aim to verify that each error would be properly identified. As shown in Fig. 2 (a), for each case, we do indeed find the corresponding syndrome pattern that identifies the location of the single-qubit error. Suppose that the expectation value of i th stabiliser is p i ; then the probability that the syndrome measurement works is |$\prod $| i (| p i | + 1)/2, which is 0.413 on average in experiment. We also apply double-qubit errors on |$\mathinner {|{T}\rangle }_L$| and find the same syndrome correlation that can always detect the existence of errors (see the online supplementary material for details). Notably, the (single-qubit or double-qubit) error-afflicted states have probabilities projecting onto the code space (around |$3.3\%$|⁠ ), verifying the power of the error-correcting code.

$Destructive syndrome detection on the logic magic state $\mathinner {|{T}\rangle }_L$. A single-qubit X-, Z- or Y-type error, which corresponds to a bit-flip, phase-flip or combined error, respectively, is applied to one of the five qubits Q1 to Q5. We destructively measure the four stabilisers and find consistent syndrome correlations that identify the quantum error.$

Destructive syndrome detection on the logic magic state |$\mathinner {|{T}\rangle }_L$|⁠ . A single-qubit X -, Z - or Y -type error, which corresponds to a bit-flip, phase-flip or combined error, respectively, is applied to one of the five qubits Q 1 to Q 5 . We destructively measure the four stabilisers and find consistent syndrome correlations that identify the quantum error.

In a functioning fault-tolerant quantum computer, operations on logical qubits are realised through a series of operations on the component physical qubits. We implement and verify three such transversal logical operations. Starting from the magic state |$\mathinner {|{T}\rangle }_L$| presented in Fig. 3 (a), we demonstrate the single logical-qubit operations X L , Y L and Z L and plot the rotated states within the code space, as shown in Fig. 3 (b), (c) and (d), respectively. To characterise these logical operations, we performed the quantum process tomography within the code space as shown in Fig. 3 (e), which reflects how well logical operations manipulate logical states. We determine gate fidelities of the logical X L , Y L and Z L operations to be |$97.2(2)\%$|⁠ , |$97.8(2)\%$| and |$97.3(2)\%$|⁠ , respectively.

$Logical operation within the code space. (a) Encoded logical state $\mathinner {|{T}\rangle }_L$ illustrated on the logical Bloch sphere. (b)–(d) Single logical-qubit operation XL, YL and ZL applied on $\mathinner {|{T}\rangle }_L$. The blue squares and vector are the initial states. The red circles and vectors are the final states. The states are projected into the code space. The fidelities of the state after gate operation are 98.6(1)%, 98.0(1)% and 98.7(1)% for (b), (c) and (d), respectively. The white arrow illustrates the dynamics under the gate operation. (e) The χL matrix of the logical XL operation determined via quantum process tomography in the code space. The gate fidelity of logical XL operation is determined to be 97.2(2)%. The black-outlined hollow bars correspond to the ideal X gate. We refer the reader to the online supplementary material for the definition of the χL matrix and details.$

Logical operation within the code space. (a) Encoded logical state |$\mathinner {|{T}\rangle }_L$| illustrated on the logical Bloch sphere. (b)–(d) Single logical-qubit operation X L , Y L and Z L applied on |$\mathinner {|{T}\rangle }_L$|⁠ . The blue squares and vector are the initial states. The red circles and vectors are the final states. The states are projected into the code space. The fidelities of the state after gate operation are 98.6(1)%, 98.0(1)% and 98.7(1)% for (b), (c) and (d), respectively. The white arrow illustrates the dynamics under the gate operation. (e) The χ L matrix of the logical X L operation determined via quantum process tomography in the code space. The gate fidelity of logical X L operation is determined to be 97.2(2)%. The black-outlined hollow bars correspond to the ideal X gate. We refer the reader to the online supplementary material for the definition of the χ L matrix and details.

Finally, after encoding the single-qubit input state into the logical state, we apply the decoding circuit, see Fig. 4 (a), to map it back to the input state. With input states |$\mathinner {|{0}\rangle }$|⁠ , |$\mathinner {|{1}\rangle }$|⁠ , |$\mathinner {|{+}\rangle }$|⁠ , and |$\mathinner {|{+i}\rangle }$|⁠ , we determine the state fidelity after decoding as 87.4(5)%, 91.6(4)%, 76.7(6)%, and 77.1(6)%, respectively. The relatively lower fidelities for |$\mathinner {|{+}\rangle }$| and |$\mathinner {|{+i}\rangle }$| states are also caused by the short dephasing time. After quantum process tomography from the four output states, the process fidelity is determined as |$74.5(6)\%$|⁠ , as shown in Fig. 4 (b). The decoding circuit only applies operations on three qubits, highlighting the ability of quantum secret sharing with the five-qubit code [ 29 ]. This simplification is due to a consequence of locality: no observable on Q 1 can be affected by the omitted independent gate operations of the other qubits.

Decoding of the five-qubit code. (a) Decoding quantum circuit. After the logical state prepared with the encoding circuit shown in Fig. 1 (b), we apply the decoding circuit to map the state back to a single-qubit state. The decoding circuit is essentially a reverse encoding circuit, except the gates applied on Q 3 and Q 4 are omitted because they do not affect the final decoded qubit. (b) The χ L matrix of the encoding and decoding circuits. The color bars are the experimental χ L matrix and the black-outlined hollow bars correspond to the identical process. The process fidelity reaches 74.5(6)%.

An essential milestone on the road to fault-tolerant quantum computing is the achievement of error-corrected logical qubits that genuinely benefit from error correction, outperforming simple physical qubits. There are three steps for achieving this goal: (1) realising encoded logical qubits in a code capable of detecting and correcting errors, (2) realising operations on encoded qubits and error-correction cycles and (3) adding more ancillary qubits and improving the operation fidelity to achieve fault tolerance. Our experiment completes step (1) by realising the basic ingredients of the full functional five-qubit error-correcting code. Our work partially achieves step (2) as we indeed perform logical operations and verify error detection; however, because we are only able to evaluate stabilisers destructively, we cannot perform full error correction. Directions for future works include the realisation of non-destructive error detection [ 25 , 26 , 30 ] and error correction, and the implementation of logical operations on multiple logical qubits for the five-qubit code. Our work also has applications in error mitigation for near-term quantum computing [ 31 ].

All data analysed to evaluate the conclusions are available from the authors upon reasonable request.

The authors thank the USTC Center for Micro- and Nanoscale Research and Fabrication, Institute of Physics CAS and National Center for Nanoscience and Technology for supporting the sample fabrication. The authors also thank QuantumCTek Co., Ltd. for supporting the fabrication and maintenance of room-temperature electronics.

This work was supported by the National Key Research and Development Program of China (2017YFA0304300, 2017YFA0303900 and 2017YFA0304004), the National Natural Science Foundation of China (11875173, 11674193, 11574380 and 11905217), the Chinese Academy of Sciences, the Science and Technology Committee of Shanghai Municipality (16DZ2260100), the Anhui Initiative in Quantum Information Technologies, and the Engineering and Physical Sciences Research Council (EP/M013243/1 to S.C.B and X.Y.).

X.M., Y.-A.C., X.-B.Z. and J.-W.P. conceived the research. M.G., X.Y., X.M. and X.-B.Z. designed the experiment. S.-Y.W. designed the sample. H.D. and H.R. prepared the sample. X.Y., Z.Z., Q.Z., Y.-C.L. and H.L. designed the quantum circuit. M.G., Y.-L.W., Y.-W.Z., C.Z. and S.-W.L. carried out the experiments. Y.-L.W. developed the programming platform for measurements. M.G., X.Y., Y.-W.Z., C.Z., S.B., X.M., Y.-A.C. and X.-B.Z. analysed the results. F.-T.L., J.L., Y.X. and C.-Z.P. developed room-temperature electronics equipment. All authors contributed to discussions of the results and development of the manuscript. X.-B.Z. and J.-W.P. supervised the whole project.

Conflict of interest statement. None declared.

Shor PW . Algorithms for quantum computation: discrete logarithms and factoring . In: Proceedings 35th Annual Symposium on Foundations of Computer Science . Los Alamitos, CA : IEEE Computer Society Press , 1994 , 124 – 34 .

Google Scholar

Google Preview

Lloyd S. Universal quantum simulators . Science 1996 ; 273 : 1073 – 8 . 10.1126/science.273.5278.1073

Gottesman D. Theory of fault-tolerant quantum computation . Phys Rev A 1998 ; 57 : 127 – 37 . 10.1103/PhysRevA.57.127

Shor PW. Scheme for reducing decoherence in quantum computer memory . Phys Rev A 1995 ; 52 : R2493 – 6 . DOI: 10.1103/physreva.52.r2493

Steane AM. Error correcting codes in quantum theory . Phys Rev Lett 1996 ; 77 : 793 – 7 . 10.1103/PhysRevLett.77.793

Bennett CH , DiVincenzo DP , Smolin JA et al. Mixed-state entanglement and quantum error correction . Phys Rev A 1996 ; 54 : 3824 – 51 . 10.1103/PhysRevA.54.3824

Laflamme R , Miquel C , Paz JP et al. Perfect quantum error correcting code . Phys Rev Lett 1996 ; 77 : 198 – 201 . Doi: 10.1103/PhysRevLett.77.198

Knill E. Quantum computing with realistically noisy devices . Nature 2005 ; 434 : 39 – 44 . 10.1038/nature03350

Aliferis P , Gottesman D , Preskill J. Quantum accuracy threshold for concatenated distance-3 codes . Quantum Info Comput 2006 ; 6 : 97 – 165 .

Chiaverini J , Leibfried D , Schaetz T et al. Realization of quantum error correction . Nature 2004 ; 432 : 602 – 5 . 10.1038/nature03074

Schindler P , Barreiro JT , Monz T et al. Experimental repetitive quantum error correction . Science 2011 ; 332 : 1059 – 61 . 10.1126/science.1203329

Reed MD , DiCarlo L , Nigg SE et al. Realization of three-qubit quantum error correction with superconducting circuits . Nature 2012 ; 482 : 382 – 5 . 10.1038/nature10786

Waldherr G , Wang Y , Zaiser S et al. Quantum error correction in a solid-state hybrid spin register . Nature 2014 ; 506 : 204 – 7 . 10.1038/nature12919

Riste D , Poletto S , Huang MZ et al. Detecting bit-flip errors in a logical qubit using stabilizer measurements . Nat Commun 2015 ; 6 : 6983 . 10.1038/ncomms7983

Cramer J , Kalb N , Rol MA et al. Repeated quantum error correction on a continuously encoded qubit by real-time feedback . Nat Commun 2016 ; 7 : 11526 . 10.1038/ncomms11526

Wootton JR , Loss D. Repetition code of 15 qubits . Phys Rev A 2018 ; 97 : 052313 . 10.1103/PhysRevA.97.052313

Lu CY , Gao WB , Zhang J et al. Experimental quantum coding against qubit loss error . Proc Natl Acad Sci USA 2008 ; 105 : 11050 – 4 . 10.1073/pnas.0800740105

Bell B , Herrera-Martí D , Tame M et al. Experimental demonstration of a graph state quantum error-correction code . Nat Commun 2014 ; 5 : 3658 . 10.1038/ncomms4658

Linke NM , Gutierrez M , Landsman KA et al. Fault-tolerant quantum error detection . Sci Adv 2017 ; 3 : e1701074 . 10.1126/sciadv.1701074

Nigg D , Mueller M , Martinez EA et al. Quantum computations on a topologically encoded qubit . Science 2014 ; 345 : 302 – 5 . 10.1126/science.1253742

Ofek N , Petrenko A , Heeres R et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits . Nature 2016 ; 536 : 441 – 5 . DOI: 10.1038/nature18949

Campagne-Ibarcq P , Eickbusch A , Touzard S et al. Quantum error correction of a qubit encoded in grid states of an oscillator . Nature 2020 ; 584 : 368 – 72 . DOI: 10.1038/s41586-020-2603-3

Yao XC , Wang TX , Chen HZ et al. Experimental demonstration of topological error correction . Nature 2012 ; 482 : 489 – 94 . 10.1038/nature10770

Taminiau TH , Cramer J , Sar T et al. Universal control and error correction in multi-qubit spin registers in diamond . Nat Nanotechnol 2014 ; 9 : 171 – 6 .

Kelly J , Barends R , Fowler AG et al. State preservation by repetitive error detection in a superconducting quantum circuit . Nature 2015 ; 519 : 66 – 9 . 10.1038/nature14270

Andersen CK , Remm A , Lazar S et al. Repeated quantum error detection in a surface code . Nat Phys 2020 ; 16 : 875 – 80 . 10.1038/s41567-020-0920-y

Cory DG , Price MD , Maas W et al. Experimental quantum error correction . Phys Rev Lett 1998 ; 81 : 2152 – 5 . 10.1103/PhysRevLett.81.2152

Gong M , Chen MC , Zheng Y et al. Genuine 12-qubit entanglement on a superconducting quantum processor . Phys Rev Lett 2019 ; 122 : 110501 . Doi: 10.1103/PhysRevLett.122.110501

Cleve R , Gottesman D , Lo HK. How to share a quantum secret . Phys Rev Lett 1999 ; 83 : 648 – 51 . Doi: 10.1103/PhysRevLett.83.648

Bultink CC , O’Brien TE , Vollmer R et al. Protecting quantum entanglement from leakage and qubit errors via repetitive parity measurements . Sci Adv 2020 ; 6 : eaay3050 . 10.1126/sciadv.aay3050

McClean JR , Jiang Z , Rubin NC et al. Decoding quantum errors with subspace expansions . Nat Commun 2020 ; 11 : 636 . 10.1038/s41467-020-14341-w

Author notes

Supplementary data.

Month:	Total Views:
January 2021	171
February 2021	98
March 2021	185
April 2021	63
May 2021	59
June 2021	58
July 2021	31
August 2021	38
September 2021	40
October 2021	32
November 2021	53
December 2021	38
January 2022	171
February 2022	213
March 2022	187
April 2022	183
May 2022	203
June 2022	114
July 2022	201
August 2022	139
September 2022	371
October 2022	444
November 2022	311
December 2022	278
January 2023	211
February 2023	160
March 2023	196
April 2023	306
May 2023	130
June 2023	86
July 2023	104
August 2023	84
September 2023	74
October 2023	108
November 2023	89
December 2023	82
January 2024	108
February 2024	70
March 2024	111
April 2024	117
May 2024	82
June 2024	105
July 2024	109
August 2024	41

Email alerts

Citing articles via.

Recommend to Your Librarian

Affiliations

Online ISSN 2053-714X
Print ISSN 2095-5138
Copyright © 2024 China Science Publishing & Media Ltd. (Science Press)
About Oxford Academic
Publish journals with us
University press partners
What we publish
New features
Open access
Institutional account management
Rights and permissions
Get help with access
Accessibility
Advertising
Media enquiries
Oxford University Press
Oxford Languages
University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

Copyright © 2024 Oxford University Press
Cookie settings
Cookie policy
Privacy policy
Legal notice

This Feature Is Available To Subscribers Only

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

View all journals
Explore content
About the journal
Publish with us
Sign up for alerts
Published: 22 April 2014

Experimental demonstration of a graph state quantum error-correction code

B. A. Bell 1 ,
D. A. Herrera-Martí 2 ,
M. S. Tame 3 , 4 ,
D. Markham 5 ,
W. J. Wadsworth 6 &
J. G. Rarity 1

Nature Communications volume 5 , Article number: 3658 ( 2014 ) Cite this article

5802 Accesses

84 Citations

1 Altmetric

Metrics details

Quantum information
Quantum optics

Scalable quantum computing and communication requires the protection of quantum information from the detrimental effects of decoherence and noise. Previous work tackling this problem has relied on the original circuit model for quantum computing. However, recently a family of entangled resources known as graph states has emerged as a versatile alternative for protecting quantum information. Depending on the graph’s structure, errors can be detected and corrected in an efficient way using measurement-based techniques. Here we report an experimental demonstration of error correction using a graph state code. We use an all-optical setup to encode quantum information into photons representing a four-qubit graph state. We are able to reliably detect errors and correct against qubit loss. The graph we realize is setup independent, thus it could be employed in other physical settings. Our results show that graph state codes are a promising approach for achieving scalable quantum information processing.

You have full access to this article via your institution.

Parity-encoding-based quantum computing with Bayesian error tracking

Error-protected qubits in a silicon photonic chip

Graph states of atomic ensembles engineered by photon-mediated entanglement

Introduction.

Quantum error-correcting codes (QECCs) constitute fundamental building blocks in the design of quantum computer architectures 1 . It was realized early on that using QECCs 2 , 3 , 4 , 5 , 6 to counteract the effects of decoherence and noise provides a means to increase the coherence time of the encoded information. This enhancement is crucial for enabling a range of speedups in quantum algorithms. Here, the threshold theorem 7 ensures that a quantum computer built with faulty, unreliable components can still be used reliably to implement quantum tasks using QECC techniques 8 , 9 , so long as the noise affecting its parts is below a given threshold. A great deal of effort is currently being invested in designing new quantum codes to increase the threshold. In this context, a computational paradigm, especially well suited for quantum error correction, is measurement-based quantum computation 10 , 11 , 12 (MBQC), in which a resource state consisting of many entangled qubits is prepared before the computation starts. In MBQC, an algorithm is enacted by performing sequential measurements on the resource state in such a way that the output of the computation is stored in the unmeasured qubits. Photonic technologies 13 have enjoyed enormous success in the generation of a variety of resource states for MBQC 14 , 15 , 16 , 17 , 18 and in the implementation of computational primitives 19 , 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 . Importantly, QECCs can be embedded in the resource states for MBQC in several inequivalent ways 33 , 34 , 35 , and of particular theoretical interest, due to their large thresholds, are the topological QECC embeddings 36 , 37 , 38 , 39 , 40 , 41 , 42 . However, while there has been an experimental proof-of-principle for topological encoding 43 , overall these codes remain largely out of reach of current technologies due to the size and complexity of the resources required. An alternative and more compact approach is offered by the theory of graph codes 44 , 45 , 46 , 47 , where very general QECCs can be used within the framework of MBQC to account for different noise scenarios. Graph codes are based on the stabilizer formalism and are thus relevant for both MBQC and the original circuit model.

In this work, we report the experimental demonstration of a quantum error-correcting graph code. We have used an all-optical setup to encode quantum information into photons representing the code. The experiment was carried out for the smallest graph code capable of detecting one quantum error, namely the four-qubit code 48 , 49 , 50 [[4,1,2]]. Here, [[ n,k,d ]] is the standard notation for QECCs, where n denotes the number of physical qubits, k is the number of logical qubits encoded and d is the distance, which indicates how many errors can be tolerated and depends on information about the error: a code of distance d can correct up to ⌊ ( d −1)/2 ⌋ arbitrary errors at unspecified locations. On the other hand, if we know where the error occurs, the code can correct up to d −1 errors (equivalently erasures or loss errors), or it can detect up to d −1 errors at unspecified locations (without necessarily being able to correct them). The four-qubit code used in our experiment has a distance of d =2, so it can correct up to one quantum error or a loss error at a known location and can detect up to one quantum error at an unknown location. This has applications in several key areas of quantum technologies besides the obvious goal of fault-tolerance 51 , 52 , 53 , 54 , for example in communication over lossy channels, lossy interferometry and secret sharing. Previous experiments have realized error-correcting codes of compact size, such as the 3-qubit code in an ion-trap setup 55 . One of the key benefits of enlarging the code space size to the four-qubit code is that it enables more general errors, in particular loss errors, to be corrected. While the four-qubit code has been realized before in several works, most notably in ref. 56 , these studies have been restricted to quantum error-correction with the four-qubit code using the original circuit model. For example, in ref. 56 the logic gates were applied sequentially using a series of polarizing beam splitter (PBS) elements in a linear optics setup.

Here we go beyond this approach and show how to realize the code using a different experimental setup that can generate an entangled graph state in the promising context of MBQC and fully characterize its performance. One of the key distinctions of our work compared with previous studies is that the graph state resource for the code is generated first and then the quantum information is teleported into it, following closely the model for MBQC. This allows us to transfer arbitrary qubits into the code as well as preparing the logical subspaces in a given state. This is an important distinction, as the quantum information to be encoded is untouched during the generation of the code resource. In this way, if the entanglement process fails, we can start again without the quantum information being lost, which means that our work cannot be re-interpreted as the quantum circuit used in ref. 56 . We show that by measuring an external ancilla qubit, its information in the Bloch sphere can be transferred into the logical subspace of the code, which after undergoing a noisy channel can be decoded to retrieve the original information with high quality. These encoding and decoding operations are straightforwardly extended to larger codes, as they rely on an appropriate graph state connectivity 45 , 46 , 47 and can always be achieved via local qubit interactions. Importantly, this procedure also lends itself to variations where the number of encoded qubits can increase (in the case of larger codes) at the expense of reducing the distance d , by modifying the shape of the total graph. This is relevant in order to boost the code rate, k / n , for the erasure channel 7 , 50 . Recent experimental work incorporating quantum error correction using a measurement-based approach with tree-like graph state resources has considered basic protection against loss 56 and for the case of phase errors using a box-type graph where the location of the error is known 57 , 58 . In this work, we lift these restrictions and experimentally demonstrate a graph code using a different type of graph state that can be described within the MBQC framework to provide protection against general errors and loss, where the location of the error is known, as well as the detection of general quantum errors where the location is unknown. In our experiment, we generate the graph state resource via the method of fusion 59 . This has several advantages over interferometric methods 19 , such as overall stability of the setup and, in principle, scalability to larger graph states. We successfully demonstrate all elements of error correction in our experiment, including in sequence the encoding, detection and correction of errors, and we verify the quality of each of these steps separately. Demonstrations of compact QECC schemes, such as the one we have performed, are of the utmost importance to the design and characterization of noise protection in a number of different physical architectures at present. They constitute the necessary first steps towards large-scale quantum computers. Our experimental demonstration and its full analysis contribute to helping achieve these first steps.

Resource state characterization

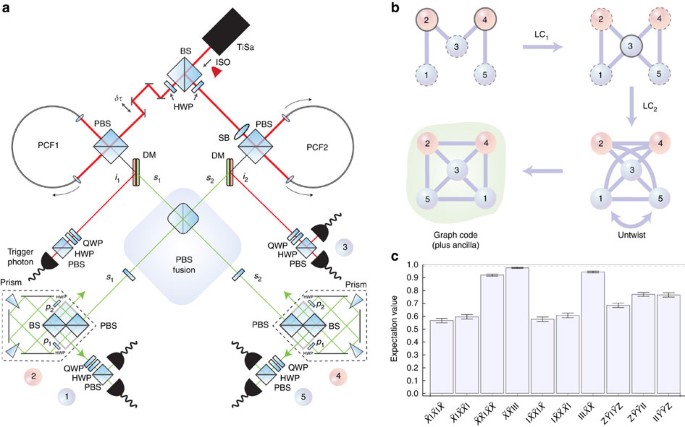
where the error has been calculated using a Monte Carlo method with Poissonian noise on the count statistics 65 . The negative value of the witness indicates the presence of GME, confirming that all qubits are involved in the generation of the resource. The individual expectation values forming the expression for the witness are shown in Fig. 1c . Using seventeen measurement bases (see Methods) we obtain the fidelity of the graph state of F =0.70±0.01.

In order to check the persistency of entanglement in the resource, we measure the ancilla qubit using a Z measurement, thus removing it from the graph. For the case that the state |0› 3 is measured, the remaining four qubits should be left in the logical code state |+ L ›, which corresponds to a ‘box’ cluster state,

Using the relevant witness in ref. 66 (see Methods) we find the value

showing GME persists even when the ancilla qubit is removed. Using nine measurement bases (see Methods), we obtain the fidelity of the box cluster state of F =0.73±0.01, consistent with the quality of the initial five-qubit graph state.

Encoding logical states

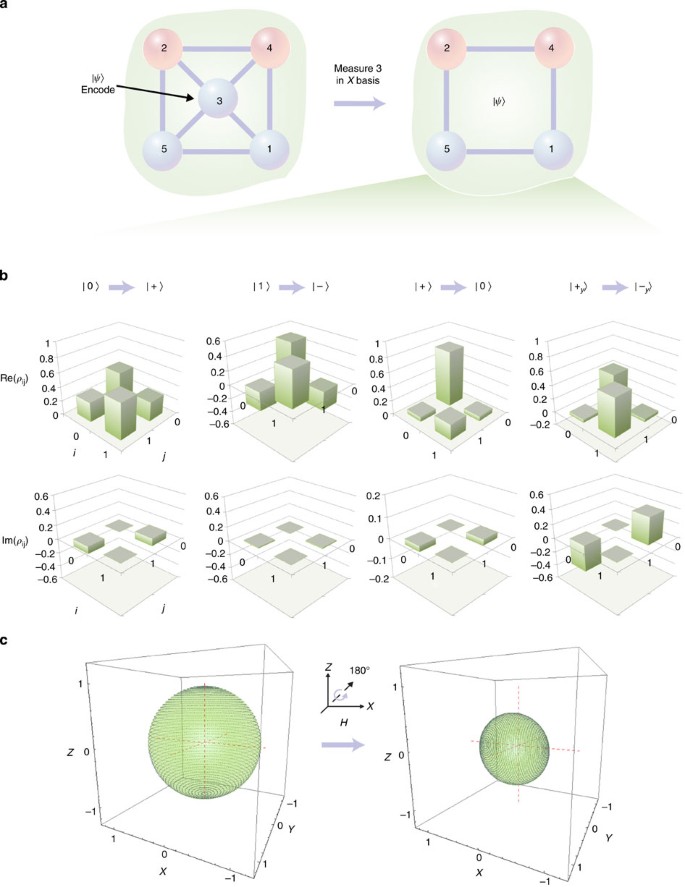
Loss tolerance

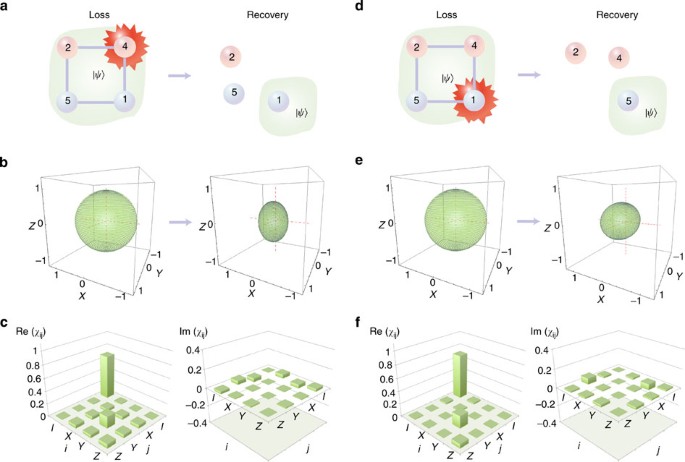
( a ) General scenario of loss tolerance for the four-qubit graph code. Here any one of the four qubits may be lost. In the first case, qubit 4 has been lost by combining the two paths corresponding to the computational basis of the qubit. The encoded qubit can be recovered on qubit 1 using the measurements and results of the remaining qubits 2 and 5 as described in the main text. ( b ) Path qubit lost with the recovery treated as a channel. Here the Bloch sphere representation is used to show the original qubit states and the recovered qubit states. ( c ) The χ matrix representation of the channel, showing the real part (left) and imaginary part (right). Ideally the χ matrix has only one component, the entry I I , corresponding to the identity operation. ( d ) In the second case, qubit 1 has been lost by combining the two polarizations corresponding to the computational basis of the qubit. The encoded qubit is recovered on qubit 5 using the measurements and results of the remaining qubits 2 and 4. ( e ) Polarization qubit loss with the recovery treated as a channel. Here the Bloch sphere representation shows the original qubit states and the recovered qubit states. ( f ) The χ matrix representation of the channel, showing the real part (left) and imaginary part (right).

Quantum error detection and correction

Finally, we check the graph code’s ability to detect general quantum errors. To see this note that the logical code states are all common eigenstates of the stabilizer operators S 1 = Y 1 Z 2 Z 4 Y 5 = K 1 K 5 , S 2 = Y 1 Z 2 Y 4 Z 5 = K 1 K 4 and S 3 = Z 1 Y 2 Y 4 Z 5 = K 4 K 2 , where the K i are the original graph state stabilizer operators 10 , 11 . If there is a phase flip Z on any one qubit of the code, as shown in Fig. 4a , we can locate the error by measuring all three stabilizers without disturbing the graph code and correct the error as ‹ S i ›=1 and ‹ S i Z j ›=−1 for a given j and two of the stabilizers. Thus measuring the stabilizers performs the role of syndrome measurements for the graph code. In Fig. 4a , we show the values of the stabilizers measured in our experiment when there is a Z error on each of the qubits for all the probe states. The experimental values agree well with the theory with all having the correct sign and an error of 0.02 or less. As an arbitrary state can be written as a superposition of the probe states, the results show that any state can be encoded into the code and the error detected. Similar arguments about the stabilizers hold for Y errors, as shown in Fig. 4b with the experimental values measured for the probe states. On the other hand, if there is a bit flip X on any one qubit, it can be detected by measuring the stabilizers, but it cannot be located, since an X error anticommutes with all stabilizers: ‹ S i X j ›=−1 for a given j and all i , as shown by the experimental values in Fig. 4c . This is the reason (along with a degeneracy in locating Z and Y errors) why the code can only detect general quantum errors ( X , Y or Z ) acting on an unknown single qubit, but cannot correct them. If an error is detected via the stabilizers, then the state is discarded and one starts a given quantum protocol again by re-encoding. On the other hand, if the location of the error is known, then the type of error ( X , Y or Z ) can be determined from the pattern of the stabilizer results and the error can be corrected. All expectation values of the stabilizers were found to be consistent with those expected when there was an error occurring on any one of the qubits for all probe states, thus confirming the graph code’s ability to detect unknown single-qubit errors and correct known single-qubit errors.

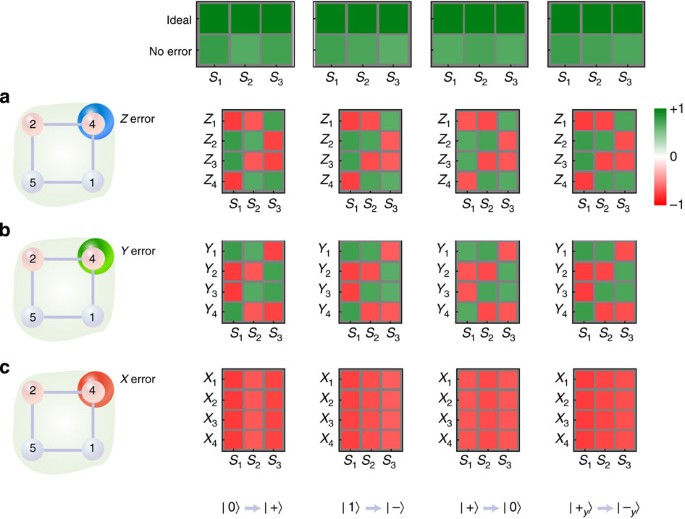
( a ) Z errors on one of the qubits of the code flips the sign of the expectation value of one or two of the stabilizer (syndrome) operators S 1 , S 2 and S 3 , as can be seen in the tables showing the experimental values for the four probe states. The values range from 0.66 to 0.79 in magnitude. The syndrome operators correspond to joint measurements, thus they can in principle be measured without disturbing the state. If no error has occurred the code can continue to be used. If an error has occurred then it will be detected and the ancilla can be encoded again to allow the continuation of a given protocol. If the error is known to be a Z Pauli operation then its location can be detected and corrected. If it is not, the ancilla must be re-encoded to allow the continuation of a given protocol. ( b ) Y errors on one of the qubits of the code also flips the sign of the expectation value of one or two of the syndrome operators. If the error is known to be a Y Pauli operation then its location can be detected and corrected. If not, the ancilla can again be re-encoded. ( c ) X errors on one of the qubits of the code flips the sign of the expectation value of all the syndrome operators. Note that if the location of the error is known, then the type of error can be inferred from the pattern of the expectation values of the syndrome operators and the error can be corrected.

In this work, we have reported the experimental demonstration of a graph state code using an all-optical setup to encode quantum information into photons representing the qubits of the code. The experiment was carried out for the smallest graph code capable of correcting up to one general quantum error or a loss error at a known location, or detecting a general quantum error at an unknown location. We showed that the graph state code can be used to correct and detect errors in a photonic setting with the results in close agreement with the theory and limited only by the quality of the initial resource state. Our demonstration and analysis provides a stimulating outlook for several applications of photonic quantum technologies besides the obvious goal of fault tolerance, for example in communication over lossy channels, lossy interferometry and secret sharing. In general, the versatility of graph codes, such as the one we have demonstrated, can further be increased by generalizing them to codeword-stabilized (CWS) codes 67 , where a given graph is supplemented with a (possibly non-additive) classical code that corrects the classical errors induced by the stabilizer structure. The theory of CWS codes is the most general theory of QECCs to date, as it encompasses graph codes, of which the four-qubit graph code we have realized is the simplest instance, and non-additive codes. Thus, the graph encoding we have demonstrated is amenable to be used with the more general CWS codes and helps to open up the playing field to more general classes of graph codes, allowing for more efficient constructions of error correction with intermediate size and applications in the near future. Moreover, the graph code and MBQC techniques we have introduced here can be readily transferred to other promising physical setups, such as ion traps, cavity-QED and superconducting qubits. The next steps will be to design and realize QECC schemes using larger graph states 45 , 46 , 47 with enhanced error-correction capabilities 70 , and introduce concatenation methods against loss errors 68 , 69 , 70 . Our experimental demonstration and characterization of a four-qubit graph code’s performance contributes to the first steps in the direction of full-scale fault-tolerant quantum information processing.

Experimental setup

The fibre source used was a birefringent PCF similar to that described in refs 28 , 59 . For a pump wavelength of 720 nm launched into the fibre’s slow axis, signal-idler pairs are generated on the fast axis at wavelengths of 626 and 860 nm, respectively. This is a turning point on the phase-matching curve for the signal wavelength, where the signal spectrum becomes uncorrelated with the pump wavelength, and hence also with the idler spectrum. This means the signal-idler pair are generated almost without spectral correlations in a pure quantum state, and do not require tight spectral filtering to show quantum interference.

To generate entangled pairs from the Sagnac loop source, the fibre axes are rotated at each end. With the fast-axis vertical at the output of the clockwise path, this direction will produce vertical photon pairs, whereas at the output of the counter clockwise direction the fast axis must be horizontal in order to produce horizontal photon pairs. These orientations also result in the pump light being launched into the correct (slow) axis. Since the pump is always cross polarized from co-propagating photons, it exits the loop from the opposite port, helping to filter it out of the signal and idler channels. A Soleil-Babinet birefringent compensator in the pump beam before the source was used to tune the relative phase between the two terms of the entangled state. The total generation rate of entangled photons (detected twofold coincidences) used in the experiment is ~9,000 per second.

The other PCF source produces horizontally polarized signal photons, which are rotated to diagonal before being fused with the signal from the entangled pair, leaving the three-photon GHZ state. It is necessary to detect the unentangled idler photon from this PCF source in order to herald the signal. The idlers from both sources are filtered with tuneable bandpass filters of ~4 nm bandwidth to remove Raman emission and other background, while 40 nm wide bandpass filters are used for the signals’ wavelength which is relatively free of background. The total generation rate of signal-idler pairs of photons for the second PCF source is again ~9,000 per second. The signal photons from both sources are fused using a PBS, which transmits horizontally polarized photons and reflects vertically polarized photons, as described in ref. 59 . In order to optimize the fusion operation, we first set the polarization of the signal photons to diagonal polarization and send them through the PBS, measuring the twofold coincidences of the output photons in diagonal polarization together with heralding by the idlers, that is, a fourfold coincidence. As the arrival time of one of the input signal photons at the PBS is delayed we find an antidip (or peak) in the coincidence rate. The visibility of this antidip provides a value that can be used to quantify the indistinguishability of the signal photons. We obtain a visibility of ~62%. This non-ideal visibility affects the overall quality of the fused state via an effective dephasing decoherence channel on the qubits, as described in more detail in ref. 59 . The visibility of 62% is consistent with the measured fidelity of the final five-qubit graph state resource generated in our experiment.

After the fusion operation at the PBS, all four photons are collected into single-mode fibres. The signals are then relaunched into path-qubit setups, which consist of displaced Sagnac interferometers built around hybrid BS cubes, with half of the coating a PBS and the other half a 50:50 BS. The photons are split at the PBS side, so their path is correlated with their polarization, and then recombined on the BS side, while the displaced Sagnac configuration gives intrinsic phase stability between the paths. Each path contains a half-wave plate, to carry out the local polarization rotations for state preparation, then a 3 mm glass plate, which can be tilted to change the phase and hence the measurement basis.

The signal photons are again collected into single-mode fibres and launched into a polarization analysis section. The entangled idler also goes into the polarization analysis section, but with space for additional optics (a wave plate or polarizer) to be inserted to encode the ancilla qubit state. Polarization analysis consists of a QWP, HWP, then a PBS, with both outputs of the PBS collected into multimode fibres coupled to silicon avalanche photodiodes 65 . The heralding idler goes straight to a detector. The detectors are connected to an eight-channel FPGA(MT-30A FPGA multichannel coincidence counter from Qumet Technologies: http://www.qumetec.com ), which allows all combinations of coincidence to be monitored within a nanosecond-timing window. The detected rate of fourfold coincidences is ~0.25 per second.

Entanglement witnesses

For the graph state corresponding to the code resource plus ancilla qubit we use the following entanglement witness on qubits 1, 2, 3, 4 and 5

where Õ corresponds to measurements in the O basis with the eigenstates swapped. This is a locally rotated version of the witness given in ref. 66 for a five-qubit linear cluster state and takes into account the local complementation operations described in Fig. 1b of the main text.

For the box cluster we use the following entanglement witness on qubits 1, 2, 4 and 5

which is a locally rotated version of the one given in ref. 66 for a four-qubit linear cluster state and takes into account the local complementation operations needed to rotate it into a box cluster.

For the rotated GHZ state, we use the following entanglement witness on qubits 1, 2, 4 and 5

which is a locally rotated version of the one given in ref. 66 .

For the maximally entangled qubit pairs in the logical encoding of the probe state |+ y ›, we use the following entanglement witness on qubit pair (1,2) and pair (4,5)

which is a locally rotated version of the one given in ref. 66 for a two-qubit linear cluster state.

Fidelity operators

For the five-qubit graph state resource, we decompose the fidelity operator into a summation of products of Pauli matrices as

Obtaining the expectation value of this operator requires 17 unique measurement bases: XXXXX , XXYYZ , XXYZY , XXZYY , XXZZZ , YYXYY , YYXZZ , YYZXX , YZYYZ , YZXZY , YZYXX , ZYYYZ , ZYZZY , ZYYXX , ZZXYY , ZZXZZ and ZZZXX .

For the four-qubit box cluster state we decompose the fidelity operator as

Obtaining the expectation value of this operator requires nine unique measurement bases: XXXX , XXYY , XXZZ , YYXX , YZYZ , YZZY , ZYYZ , ZYZY and ZZXX .

Stabilizer picture of the graph code

Additional information.

How to cite this article : Bell, B. A. et al. Experimental demonstration of a graph state quantum error-correction code. Nat. Commun. 5:3658 doi: 10.1038/ncomms4658 (2014).

Ladd, T. D. et al. Quantum computers. Nature 464 , 45–53 (2010).

Article CAS ADS Google Scholar

Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52 , R2493 (1995).

Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77 , 793–797 (1996).

Article CAS ADS MathSciNet Google Scholar

Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54 , 1098–1105 (1996).

Knill, E. & Laflamme, R. Theory of quantum error-correcting codes. Phys. Rev. A 55 , 900–911 (1997).

Preskill, J. Reliable quantum computers. Proc. R. Soc. A 454 , 385–410 (1998).

Article ADS Google Scholar

Aharonov, D. & Ben-Or, M. in Proc. 29th Ann. ACM Symp. on Theory of Computing 176ACM: New York, (1998).

Kitaev, A. Y. Quantum computations: algorithms and error correction. Russian Math. Surveys 52 , 1191–1249 (1997).

Article ADS MathSciNet Google Scholar

Knill, E., Laflamme, R. & Zurek, W. H. Resilient quantum computation: error models and thresholds. Proc. Roy. Soc. A 454 , 365–384 (1998).

Raussendorf, R. & Briegel, H. J. A one-way quantum computer. Phys. Rev. Lett. 86 , 5188–5191 (2001).

Raussendorf, R., Browne, D. E. & Briegel, H. J. Measurement-based quantum computation on cluster states. Phys. Rev. A 68 , 022312 (2003).

Briegel, H. J., Browne, D. E., Dür, W., Raussendorf, R. & Van den Nest, M. Measurement-based quantum computation. Nat. Phys. 5 , 19–26 (2009).

Article CAS Google Scholar

O'Brien, J. L., Furusawa, A. & Vuckovic, J. Photonic quantum technologies. Nat. Photonics 3 , 687–695 (2009).

Kiesel, N. et al. Experimental analysis of a 4-Qubit cluster state. Phys. Rev. Lett. 95 , 210502 (2005).

Lu, C.-Y. et al. Experimental entanglement of six photons in graph states. Nat. Phys. 3 , 91–95 (2007).

Vallone, G., Pomarico, E., Mataloni, P., De Martini, F. & Berardi, V. Realization and characterization of a 2-photon 4-qubit linear cluster state. Phys. Rev. Lett. 98 , 180502 (2007).

Park, H. S., Cho, J., Lee, J. Y., Lee, D.-H. & Choi, S.-K. Two-photon four-qubit cluster state generation based on a polarization-entangled photon pair. Opt. Express. 15 , 17960–17966 (2007).

Kalasuwan, P. et al. A simple scheme for expanding photonic cluster states for quantum information. J. Opt. Soc. Am. B 27 , A181–A184 (2010).

Walther, P. et al. Experimental one-way quantum computing. Nature 434 , 169–176 (2005).

Prevedel, R. et al. High-speed linear optics quantum computation using active feed-forward. Nature 445 , 65–69 (2007).

Tame, M. S. et al. Experimental realization of Deutsch’s algorithm in a one-way quantum computer. Phys. Rev. Lett. 98 , 140501 (2007).

Chen, K. et al. Experimental realization of one-way quantum computing with two-photon four-qubit cluster states. Phys. Rev. Lett. 99 , 120503 (2007).

Tokunaga, Y., Kuwashiro, S., Yamamoto, T., Koashi, M. & Imoto, N. Generation of high-fidelity four-photon cluster state and quantum-domain demonstration of one-way quantum computing. Phys. Rev. Lett. 100 , 210501 (2008).

Vallone, G., Pomarico, E., De Martini, F. & Mataloni, P. Active one-way quantum computation with 2-photon 4-qubit cluster states. Phys. Rev. Lett. 100 , 160502 (2008).

Biggerstaff, D. N. et al. Cluster-state quantum computing enhanced by high-fidelity generalized measurements. Phys. Rev. Lett. 103 , 240504 (2009).

Vallone, G., Donati, G., Bruno, N., Chiuri, A. & Mataloni, P. Experimental realization of the Deutsch-Jozsa algorithm with a six-qubit cluster state. Phys. Rev. A 81 , 050302(R) (2010).

Lee, S. M. et al. Experimental realization of a four-photon seven-qubit graph state for one-way quantum computation. Opt. Express 20 , 6915–6926 (2012).

Bell, B. A. et al. Experimental characterization of universal one-way quantum computing. New J. Phys. 14 , 023021 (2012).

Prevedel, R., Stefanov, A., Walther, P. & Zeilinger, A. Experimental realization of a quantum game on a one-way quantum computer. New J. Phys. 9 , 205 (2007).

Barz, S. et al. Experimental demonstration of blind quantum computing. Science 335 , 303–308 (2012).

Lavoie, J., Kaltenbaek, R., Zeng, B., Bartlett, S. D. & Resch, K. J. Optical one-way quantum computing with a simulated valence-bond solid. Nat. Phys. 6 , 850–854 (2010).

Article Google Scholar

Gao, W.-B. et al. Experimental measurement-based quantum computing beyond the cluster-state model. Nat. Photonics 5 , 117–123 (2011).

Aliferis, P. & Leung, D. W. Simple proof of fault tolerance in the graph-state model. Phys. Rev. A 73 , 032308 (2006).

Dawson, C. M., Haselgrove, H. L. & Nielsen, M. A. Noise thresholds for optical quantum computers. Phys. Rev. Lett. 96 , 020501 (2006).

Silva, M., Danos, V., Kashefi, E. & Ollivier, H. A direct approach to fault-tolerance in measurement-based quantum computation via teleportation. New J. Phys. 9 , 192 (2007).

Raussendorf, R., Harrington, J. & Goyal, K. A fault-tolerant one-way quantum computer. Ann. Phys. 321 , 2242–2270 (2006).

Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98 , 190504 (2007).

Bravyi, S. & Raussendorf, R. Measurement-based quantum computation with the toric code states. Phys. Rev. A 76 , 022304 (2007).

Barrett, S. D. & Stace, T. M. Fault tolerant quantum computation with very high thresholds for loss errors. Phys. Rev. Lett. 105 , 200502 (2010).

Fujii, K. & Tokunaga, Y. Fault-tolerant topological one-way quantum computation with probabilistic two-qubit gates. Phys. Rev. Lett. 105 , 250503 (2010).

Fujii, K. & Yamamoto, K. Cluster-based architecture for fault-tolerant quantum computation. Phys. Rev. A 81 , 042324 (2010).

Herrera-Martí, D. A., Fowler, A. G., Jennings, D. & Rudolph, T. Photonic implementation for the topological cluster-state quantum computer. Phys. Rev. A 82 , 032332 (2010).

Yao, X.-C. et al. Experimental demonstration of topological error correction. Nature 482 , 489–494 (2012).

Hein, M. et al. Entanglement in graph states and its applications. Proc. Int. Sch. Phys. E. Fermi ‘Quantum Computers, Algorithms and Chaos’, Varenna (2005). Preprint at http://arxiv.org/abs/quant-ph/0602096 (2006).

Schlingemann, D. & Werner, R. F. Quantum error-correcting codes associated with graphs. Phys. Rev. A 65 , 012308 (2001).

Schlingemann, D. Stabilizer codes can be realized as graph codes. Quant. Inf. Comp. 2 , 307–323 (2002).

MathSciNet MATH Google Scholar

Schlingemann, D. Logical network implementation for graph codes and cluster states. Quant. Inf. Comp. 3 , 431–449 (2003).

Vaidman, L., Goldenberg, L. & Wiesner, S. Error prevention scheme with four particles. Phys. Rev. A 54 , 1745–1748 (1996).

Leung, D. W., Nielsen, M. A., Chuang, I. L. & Yamamoto, Y. Approximate quantum error correction can lead to better codes. Phys. Rev. A 56 , 2567–2573 (1997).

Grassl, M., Beth, T. & Pellizari, T. Codes for the quantum erasure channel. Phys. Rev. A 56 , 33–38 (1997).

Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409 , 46–52 (2001).

Knill, E. Quantum computing with realistically noisy devices. Nature 434 , 39–44 (2005).

Knill, E. Fault-Tolerant Postselected Quantum Computation: Schemes. Preprint at http://arxiv.org/abs/quant-ph/0402171 (2004).

Knill, E. Scalable quantum computing in the presence of large detected-error rates. Phys. Rev. A 71 , 042322 (2005).

Chiaverini, J. et al. Realization of quantum error correction. Nature 432 , 602–605 (2004).

Lu, C.-Y. et al. Experimental quantum coding against qubit loss error. Proc. Natl Acad. Sci. USA 105 , 11050–11054 (2008).

Barz, S. et al. Demonstrating elements of measurement-based quantum error correction. Preprint at http://arxiv.org/abs/1308.5209 (2013).

Lanyon, B. P. et al. Measurement-based quantum computation with trapped ions. Phys. Rev. Lett. 111 , 210501 (2013).

Bell, B. et al. Experimental characterization of photonic fusion using fibre sources. New J. Phys. 15 , 053030 (2013).

Fulconis, J., Alibart, O., O’Brien, J. L., Wadsworth, W. J. & Rarity, J. G. Nonclassical interference and entanglement generation using a photonic crystal fiber pair photon source. Phys. Rev. Lett. 99 , 120501 (2007).

Clark, A. et al. Intrinsically narrowband pair photon generation in microstructured fibres. New J. Phys. 13 , 065009 (2011).

Halder, M. et al. Nonclassical 2-photon interference with separate intrinsically narrowband fibre sources. Opt. Express 17 , 4670–4676 (2009).

Browne, D. E. & Rudolph, T. Resource-efficient linear optical quantum computation. Phys. Rev. Lett. 95 , 010501 (2005).

Pan, J. & Zeilinger, A. Greenberger-Horne-Zeilinger-state analyzer. Phys. Rev. A 57 , 2208 (1998).

James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64 , 052312 (2001).

Tóth, G. & Gühne, O. Detecting genuine multipartite entanglement with two local measurements. Phys. Rev. Lett. 94 , 060501 (2005).

Cross, A., Smith, G., Smolin, J. & Zeng, B. Codeword stabilized quantum codes. IEEE Int. Symp. Inf. Th. 364–368 (2008).

Cross, A., Smith, G., Smolin, J. A. & Zeng, B. Codeword stabilized quantum codes. IEEE Trans. Inf. Th. 55 , 433–438 (2009).

Article MathSciNet Google Scholar

Herrera-Martí, D. A. & Rudolph, T. Loss tolerance with a concatenated graph state. Quant. Inf. Comp. 13 , 0995 (2013).

MathSciNet Google Scholar

Varnava, M., Browne, D. E. & Rudolph, T. Loss tolerance in one-way quantum computation via counterfactual error correction. Phys. Rev. Lett. 97 , 120501 (2006).

Download references

Acknowledgements

We thank T. Rudolph for theory discussions, and A. McMillan and R. Nock for experimental discussions. This work was supported by the UK’s Engineering and Physical Sciences Research Council, ERC grant 247462 QUOWSS, the National Research Foundation and Ministry of Education, Singapore, the Leverhulme Trust, the HIPERCOM (2011-CHRI-006) project and the Ville de Paris Emergences program, project CiQWii.

Author information

Authors and affiliations.

Department of Electrical and Electronic Engineering, Centre for Communications Research, University of Bristol, Merchant Venturers Building, Woodland Road, Bristol, BS8 1UB, UK

B. A. Bell & J. G. Rarity

Centre for Quantum Technologies, National University of Singapore, 3 Science Drive 2, Singapore, 117543, Singapore

D. A. Herrera-Martí

School of Chemistry and Physics, University of KwaZulu-Natal, Durban, 4001, South Africa

National Institute for Theoretical Physics, University of KwaZulu-Natal, 4001, Durban, South Africa

Département Informatique et Réseaux, CNRS LTCI, Telecom ParisTech, 23 avenue d’Italie, CS 51327, Paris CEDEX 13, 75214, France

Department of Physics, Centre for Photonics and Photonic Materials, University of Bath, Claverton Down, Bath, BA2 7AY, UK

W. J. Wadsworth

You can also search for this author in PubMed Google Scholar

Contributions

B.A.B., D.A.H.-M., M.S.T., D.M. and J.G.R. jointly conceived the graph state error-correction scheme, the experimental layout and methodology. B.A.B. performed the experiments. M.S.T. and J.G.R. led the project. All authors discussed the results and participated in the manuscript preparation.

Corresponding authors

Correspondence to M. S. Tame or J. G. Rarity .

Ethics declarations

Competing interests.

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Bell, B., Herrera-Martí, D., Tame, M. et al. Experimental demonstration of a graph state quantum error-correction code. Nat Commun 5 , 3658 (2014). https://doi.org/10.1038/ncomms4658

Download citation

Received : 22 September 2013

Accepted : 14 March 2014

Published : 22 April 2014

DOI : https://doi.org/10.1038/ncomms4658

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Fusion of deterministically generated photonic graph states.

Philip Thomas
Leonardo Ruscio
Gerhard Rempe

Nature (2024)

Quantum teleportation based on non-maximally entangled graph states

Yuzheng Wei

Quantum Information Processing (2023)

Chip-based photonic graph states

Jieshan Huang
Xiaojiong Chen
Jianwei Wang

AAPPS Bulletin (2023)

Optical demonstration of quantum fault-tolerant threshold

Guang-Can Guo

Light: Science & Applications (2022)

Entangling logical qubits with lattice surgery

Alexander Erhard
Hendrik Poulsen Nautrup
Thomas Monz

Nature (2021)

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

Explore articles by subject
Guide to authors
Editorial policies

IMAGES

Experimental results of topological error correction. All physical
(PDF) Experimental demonstration of topological error correction
[PDF] Experimental demonstration of topological error correction
Experimental setup for the generation of the 8-qubit cluster state and
Experimental demonstration of topological error correction
Experimental results of topological error correction. All physical

COMMENTS

Experimental demonstration of topological error correction
To ensure good spatial and temporal overlap, the photons are also spectrally filtered, with full-widths at half-maximum of Δλ FWHM = 8 nm for photons 1, 3, 5 and 7 and Δλ FWHM = 2.8 nm for ...
PDF Experimental demonstration of topological error correction
Preparation of the eight-photon cluster state In our experiment, we create the desired eight-photon cluster state using spontaneous parametric down-conversion and linear optics.
Experimental demonstration of topological error correction
arXivLabs: experimental projects with community collaborators. arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Experimental demonstration of topological error correction
Affiliation 1 Shanghai Branch, National Laboratory for Physical Sciences at Microscale and Department of Modern Physics, University of Science and Technology of China, Shanghai 201315, China.
Experimental demonstration of topological error correction
FIG. S2: Topological gates with 3D cluster states. The sub-cluster C (indicated by the wire frame) realizes an encoded CNOT gate between control c and target t.
Experimental demonstration of topological error correction
Scalable quantum computing can only be achieved if qubits are manipulated fault-tolerantly. Topological error correction—a novel method which combines topological ...
Experimental demonstration of topological error correction
This paper introduces a feasible architectural design for large scale quantum computation in optical systems by combining the recent developments in topological cluster state computation with the photonic module, a simple chip-based device that can be used as a fundamental building block for a large-scale computer.
Experimental demonstration of topological error correction
We show that topological equivalence classes of circles in a two-dimensional square lattice can be used to design dynamical decoupling procedures to protect qubits attached on the edges of the ...
Experimental demonstration of topological error correction.
Lu CY, 0000-0002-8227-9177, University of Science and Technology of China Hefei National Laboratory for Physical Sciences at the Microscale. Gao WB, 0000-0003-3971-621X, Nanyang Technological University. Raussendorf R, 0000-0003-4983-9213, University of British Columbia. Nature , 22 Feb 2012, 482 (7386): 489-494.
Experimental demonstration of topological error correction
Part of the support team is currently on holidays and requests may take longer to get processed. Thanks for your patience!
Experimental demonstration of topological error correction
A new quantum interferometric scheme based on three-dimensional waveguide devices based on Fock states is proposed and theoretically investigated, expected to open new perspectives to quantum enhanced sensing and metrology performed in integrated photonics.
Experimental demonstration of topological error correction
Pub Date: February 2012 DOI: 10.1038/nature10770 arXiv: arXiv:1202.5459 Bibcode: 2012Natur.482..489Y Keywords: Quantum Physics; E-Print:
Enhancing detection of topological order by local error correction
The onset of topological order is observed by studying the expectation values of Wilson loops and open strings 24, 28, 29, 36, 37. A state consistent with \ ( { {\mathbb {Z}}}_ {2}\) topological ...
Experimental demonstration of topological error correction
Corrections. All material on this site has been provided by the respective publishers and authors. You can help correct errors and omissions. When requesting a correction, please mention this item's handle: RePEc:nat:nature:v:482:y:2012:i:7386:d:10.1038_nature10770.See general information about how to correct material in RePEc.. If you have authored this item and are not yet registered with ...
Experimental results of topological error correction. All physical
A four-physical-qubit state is generated to encode a logical qubit and high reconstruction fidelities are achieved against various errors. Beyond the inherent difference between bulk optics [8, 9 ...
Experimental demonstration of topological error correction
An icon used to represent a menu that can be toggled by interacting with this icon.
PDF Enhancing detection of topological order by local error correction
Given an experimental snapshot of all qubits in the Z or X basis, one can obtain values for all stabilizer operators in that basis, thereby identifying the locationsofall eormanyons,respectively ...
Topological error correction with a Gaussian cluster state
arXivLabs: experimental projects with community collaborators. arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Experimental demonstration of topological error correction
Enter the email address you signed up with and we'll email you a reset link.
Experimental exploration of five-qubit quantum error-correcting code
There are three steps for achieving this goal: (1) realising encoded logical qubits in a code capable of detecting and correcting errors, (2) realising operations on encoded qubits and error-correction cycles and (3) adding more ancillary qubits and improving the operation fidelity to achieve fault tolerance.
A topological route to error correction
Quantum computing is plagued by noise and small errors. An approach based on topological techniques reduces the sensitivity to errors and boosts the prospects for building practical quantum computers.
Overcoming the Zero-Rate Hashing Bound with Holographic Quantum Error
Several recent techniques for modifying topological codes with single-qubit Clifford operators have shown high resilience against pure Pauli noise. Paramount to these findings has been the...
Experimental deterministic correction of qubit loss
A deterministic correction of errors caused by qubit loss or leakage outside the computational space is demonstrated in a trapped-ion experiment by using a minimal instance of the topological ...
The x+y Floquet code: A simple example for topological quantum
arXivLabs: experimental projects with community collaborators arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website. Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is ...
Experimental demonstration of a graph state quantum error-correction
Finally, we check the graph code's ability to detect general quantum errors. To see this note that the logical code states are all common eigenstates of the stabilizer operators S1 = Y1Z2Z4Y5 ...

Save citation to file

Add to My Bibliography

Experimental demonstration of topological error correction

Similar articles

Publication types

LinkOut - more resources

Other Literature Sources

Molecular Biology Databases

Experimental demonstration of topological error correction

Cluster states and quantum computing

Topological error correction

Simpler topological cluster state

Preparation of the eight-photon cluster state

Experimental topological error correction

S.I Topological cluster state quantum computation

Topologically protected quantum gates.

Further Reading.

S.II Characterization of the 8-qubit cluster state

Experimental demonstration of topological error correction

Figures and Tables from this paper

One Citation

Experimental demonstration of topological error correction

Browse Econ Literature

More features

RePEc Biblio

Experimental demonstration of topological error correction

Corrections

Suggested Citation

RePEc Genealogy

New papers by email

EconAcademics

About RePEc

Participating archives

Privacy statement

Get papers listed

Open a RePEc archive

Get RePEc data

Internet Archive Audio

Mobile Apps

Browser Extensions

Save Page Now

Experimental demonstration of topological error correction

plus-circle Add Review comment Reviews

IN COLLECTIONS

SIMILAR ITEMS (based on metadata)

Experimental demonstration of topological error correction

Related Papers

RELATED PAPERS

RELATED TOPICS

Article Contents

Experimental exploration of five-qubit quantum error-correcting code with superconducting qubits

Author notes

Email alerts

Affiliations

This Feature Is Available To Subscribers Only

Experimental demonstration of a graph state quantum error-correction code

Similar content being viewed by others

Parity-encoding-based quantum computing with Bayesian error tracking

Error-protected qubits in a silicon photonic chip

Graph states of atomic ensembles engineered by photon-mediated entanglement

Resource state characterization

Encoding logical states

Loss tolerance

Quantum error detection and correction

Experimental setup

Entanglement witnesses

Fidelity operators

Stabilizer picture of the graph code

Acknowledgements

Author information

Contributions

Corresponding authors

Ethics declarations

Rights and permissions

About this article

Share this article

This article is cited by

Quantum teleportation based on non-maximally entangled graph states

Chip-based photonic graph states

Optical demonstration of quantum fault-tolerant threshold