mathematical representation

Mathematical Representations

• Reference work entry
• First Online: 01 January 2020
• Cite this reference work entry

• Gerald A. Goldin 2  

1054 Accesses

7 Citations

Definitions

As most commonly interpreted in education, mathematical representations are visible or tangible productions – such as diagrams, number lines, graphs, arrangements of concrete objects or manipulatives, physical models, written words, mathematical expressions, formulas and equations, or depictions on the screen of a computer or calculator – that encode, stand for, or embody mathematical ideas or relationships. Such a production is sometimes called an inscription when the intent is to focus on a specific instance without referring, even tacitly, to any interpretation of it. To call something a representation thus includes reference to some meaning or signification it is taken to have. Such representations are called external – i.e., they are external to the individual who produced them and accessible to others for observation, discussion, interpretation, and/or manipulation. Spoken language, interjections, gestures, facial expressions, movements, and postures may sometimes...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Anderson C, Scheuer N, Pérez Echeverría MP, Teubal EV (eds) (2009) Representational systems and practices as learning tools. Sense, Rotterdam

Google Scholar  

Bruner JS (1966) Toward a theory of instruction. The Belknap Press – Harvard University Press, Cambridge, MA

Common Core State Standards Initiative (2018) Preparing America’s students for success. Retrieved June 2018 from http://www.corestandards.org/

Cuoco AA, Curcio FR (2001) The roles of representation in school mathematics: NCTM 2001 yearbook. National Council of Teachers of Mathematics, Reston

Davis RB (1984) Learning mathematics: the cognitive science approach to mathematics education. Ablex, Norwood

Duval R (2006) A cognitive analysis of problems of comprehension in a learning of mathematics. Educ Stud Math 61:103–131

Article   Google Scholar  

Goldin GA (1998) Representational systems, learning, and problem solving in mathematics. J Math Behav 17:137–165

Goldin GA (2008) Perspectives on representation in mathematical learning and problem solving. In: English LD (ed) Handbook of international research in mathematics education, 2nd edn. Routledge – Taylor and Francis, London, pp 176–201

Goldin GA, Janvier, C (eds) (1998) Representations and the psychology of mathematics education: parts I and II (special issues). J Math Behav 17(1 & 2)

Goldin GA, Kaput JJ (1996) A joint perspective on the idea of representation in learning and doing mathematics. In: Steffe L, Nesher P, Cobb P, Goldin GA, Greer B (eds) Theories of mathematical learning. Erlbaum, Hillsdale, pp 397–430

Gravemeijer K, Doorman M, Drijvers P (2010) Symbolizing and the development of meaning in computer-supported algebra education. In: Verschaffel L, De Corte E, de Jong T, Elen J (eds) Use of representations in reasoning and problem solving: analysis and improvement. Routledge – Taylor and Francis, London, pp 191–208

Heinze A, Star JR, Verschaffel L (2009) Flexible and adaptive use of strategies and representations in mathematics education. ZDM 41:535–540

Hitt F (ed) (2002) Representations and mathematics visualization. Departamento de Matemática Educativa del Cinvestav – IPN, México

Janvier C (ed) (1987) Problems of representation in the teaching and learning of mathematics. Erlbaum, Hillsdale

Kaput J, Noss R, Hoyles C (2002) Developing new notations for a learnable mathematics in the computational era. In: English LD (ed) Handbook of international research in mathematics education. Erlbaum, Mahwah, pp 51–75

Lesh RA, Doerr HM (eds) (2003) Beyond constructivism: models and modeling perspectives on mathematics problem solving, learning, and teaching. Erlbaum, Mahwah

McClelland JL, Mickey K, Hansen S, Yuan A, Lu Q (2016) A parallel-distributed processing approach to mathematical cognition. Manuscript, Stanford University. Retrieved June 2018 from https://stanford.edu/~jlmcc/papers/

Moreno-Armella L, Sriraman B (2010) Symbols and mediation in mathematics education. In: Sriraman B, English L (eds) Advances in mathematics education: seeking new frontiers. Springer, Berlin, pp 213–232

Moreno-Armella L, Hegedus SJ, Kaput JJ (2008) From static to dynamic mathematics: historical and representational perspectives. Educ Stud Math 68:99–111

National Council of Teachers of Mathematics (2000) Principles and standards for school mathematics. NCTM, Reston

Newell A, Simon HA (1972) Human problem solving. Prentice-Hall, Englewood Cliffs

Novack MA, Congdon EL, Hermani-Lopez N, Goldin-Meadow S (2014) From action to abstraction: using the hands to learn math. Psychol Sci 25:903–910

Palmer SE (1978) Fundamental aspects of cognitive representation. In: Rosch E, Lloyd B (eds) Cognition and categorization. Erlbaum, Hillsdale, pp 259–303

Roth W-M (ed) (2009) Mathematical representation at the interface of body and culture. Information Age, Charlotte

Skemp RR (ed) (1982) Understanding the symbolism of mathematics (special issue). Visible Language 26(3)

van Garderen D, Scheuermann A, Poch A, Murray MM (2018) Visual representation in mathematics: special education teachers’ knowledge and emphasis for instruction. Teach Educ Spec Educ 41:7–23

Download references

Author information

Authors and affiliations.

Graduate School of Education, Rutgers University, New Brunswick, NJ, USA

Gerald A. Goldin

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Gerald A. Goldin .

Editor information

Editors and affiliations.

Department of Education, Centre for Mathematics Education, London South Bank University, London, UK

Stephen Lerman

Section Editor information

Department of Science Teaching, The Weizmann Institute of Science, Rehovot, Israel

Ruhama Even

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this entry

Cite this entry.

Goldin, G.A. (2020). Mathematical Representations. In: Lerman, S. (eds) Encyclopedia of Mathematics Education. Springer, Cham. https://doi.org/10.1007/978-3-030-15789-0_103

Download citation

DOI : https://doi.org/10.1007/978-3-030-15789-0_103

Published : 23 February 2020

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-15788-3

Online ISBN : 978-3-030-15789-0

eBook Packages : Education Reference Module Humanities and Social Sciences Reference Module Education

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

An editorially independent publication supported by the Simons Foundation.

Get the latest news delivered to your inbox.

Type search term(s) and press enter

• Comment Comments
• Save Article Read Later Read Later

The ‘Useless’ Perspective That Transformed Mathematics

June 9, 2020

Mathematicians can better understand aspects of complicated objects, such as the Lie group visualized here, by representing them with simpler concepts.

Introduction

When representation theory emerged in the late 19th century, many mathematicians questioned its worth. In 1897, the English mathematician William Burnside wrote that he doubted that this unorthodox perspective would yield any new results at all.

“Basically what [Burnside was] saying is that representation theory is useless,” said Geordie Williamson of the University of Sydney in a 2015 lecture .

More than a century since its debut, representation theory has served as a key ingredient in many of the most important discoveries in mathematics. Yet its usefulness is still hard to perceive at first.

“It doesn’t seem immediately clear that this is a reasonable thing to study,” said Emily Norton of the Technical University of Kaiserslautern in Germany.

Representation theory is a way of taking complicated objects and “representing” them with simpler objects. The complicated objects are often collections of mathematical objects — like numbers or symmetries — that stand in a particular structured relationship with each other. These collections are called groups. The simpler objects are arrays of numbers called matrices, the core element of linear algebra. While groups are abstract and often difficult to get a handle on, matrices and linear algebra are elementary.

“Mathematicians basically know everything there is to know about matrices. It’s one of the few subjects of math that’s thoroughly well understood,” said Jared Weinstein of Boston University.

To see how groups can be represented by matrices, it’s worth thinking about each object in turn.

First, we have groups. To take a straightforward example, consider the six symmetries of an equilateral triangle:

• Two rotational symmetries (by 120 and 240 degrees)
• Three reflection symmetries (across lines drawn from each vertex through the midpoint of the opposite side)
• One identity symmetry, in which you do nothing to the triangle at all

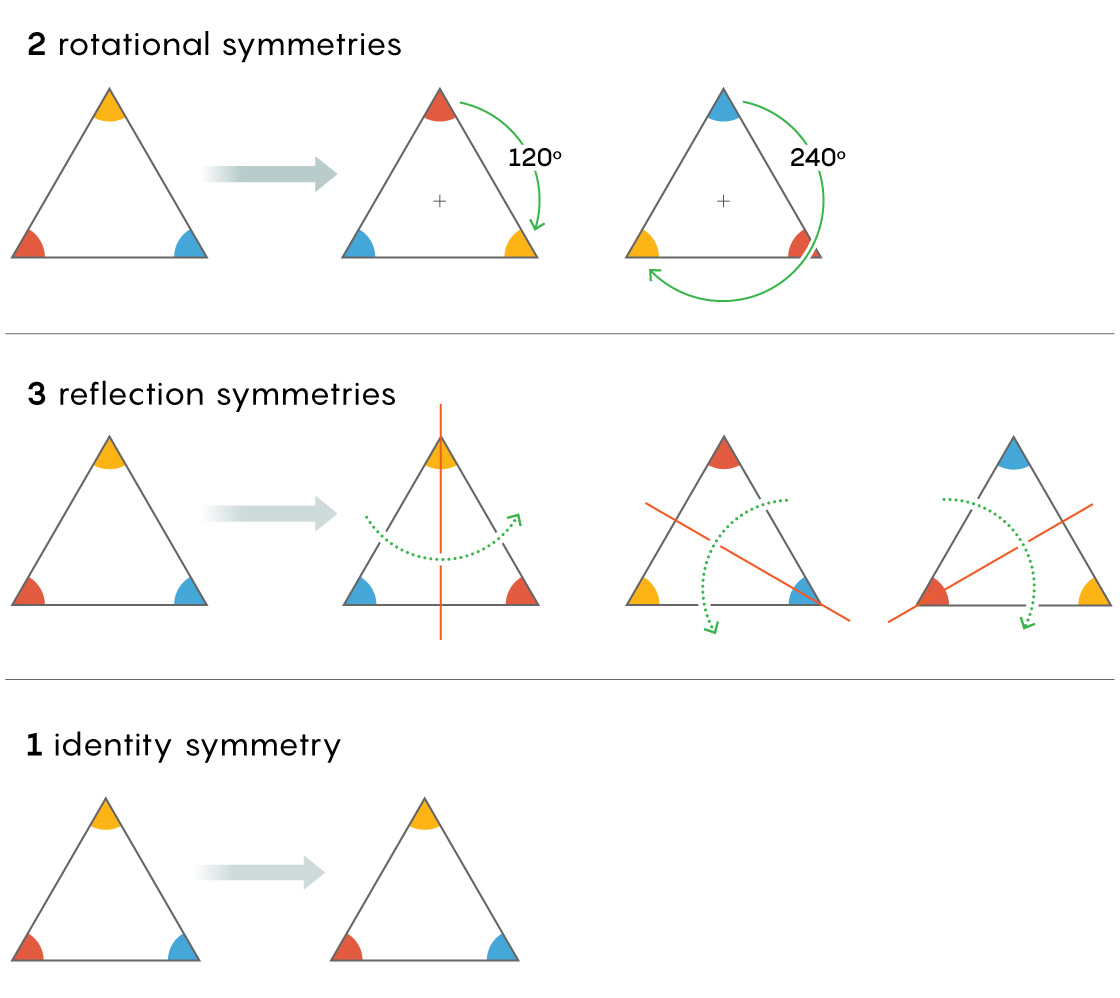
5W Infographics for Quanta Magazine

These six symmetries form a closed universe of elements — a group — whose formal name is S 3 . They form a group because you can apply any number of them to the triangle in a row, in any order, and the end result will be the same as if you’d applied just one symmetry. For example, reflecting the triangle and then rotating it 120 degrees reorders the vertices the same way as if you’d merely performed a different reflection.

“I do something and then something else. The important thing is the result is still a symmetry of the triangle,” Norton said.

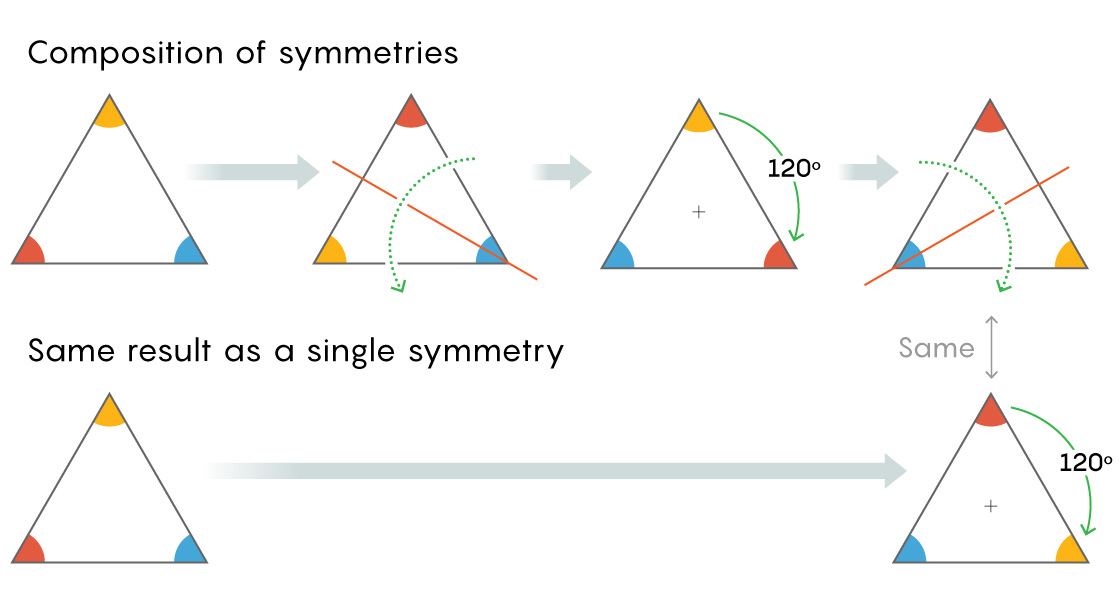
Mathematicians refer to the combination of two symmetries as a composition: One action from the group (a reflection) composed with another (a rotation) yields a third (a different reflection). You can consider composition an act of multiplication, as mathematicians do.

“We like to think of our operations as multiplications even though I’m not multiplying numbers; I’m multiplying transformations,” Norton said.

This is easiest to see if you consider the non-zero real numbers, which also form a group. The real numbers have an identity element — the number 1. Any real number composed with, or multiplied by, 1 remains unchanged. You can also multiply any combination of real numbers, in any order you want, and the product is always also a real number. Mathematicians say the group of real numbers is “closed” under multiplication, meaning that you never leave the group just by multiplying elements.

Since their discovery in the 1830s, groups have become one of the most important objects in mathematics. They encode information about prime numbers, geometric spaces and nearly all the things mathematicians care about most. Solving an important problem often turns on understanding the particular group it’s related to. But most groups are far more difficult to understand than the symmetry group of an equilateral triangle. Instead of six elements, “Lie groups,” for example, contain infinitely many.

“Sometimes groups get pretty damn complicated,” Weinstein said.

That brings us to representation theory, which converts the sometimes mysterious world of groups into the well-trammeled territory of linear algebra.

Linear algebra is the study of simple transformations performed on objects called vectors, which are effectively directed line segments. These objects are defined by coordinates, which can be displayed in the form of a matrix, an array of numbers.

The transformations occur when another matrix is applied to the vector. For example, applying the matrix

$latex \left[\begin{array}{ll}2 & 0 \\ 0 & 2\end{array}\right]$

to a given vector stretches it out by a factor of two. This is an example of a “linear” transformation.

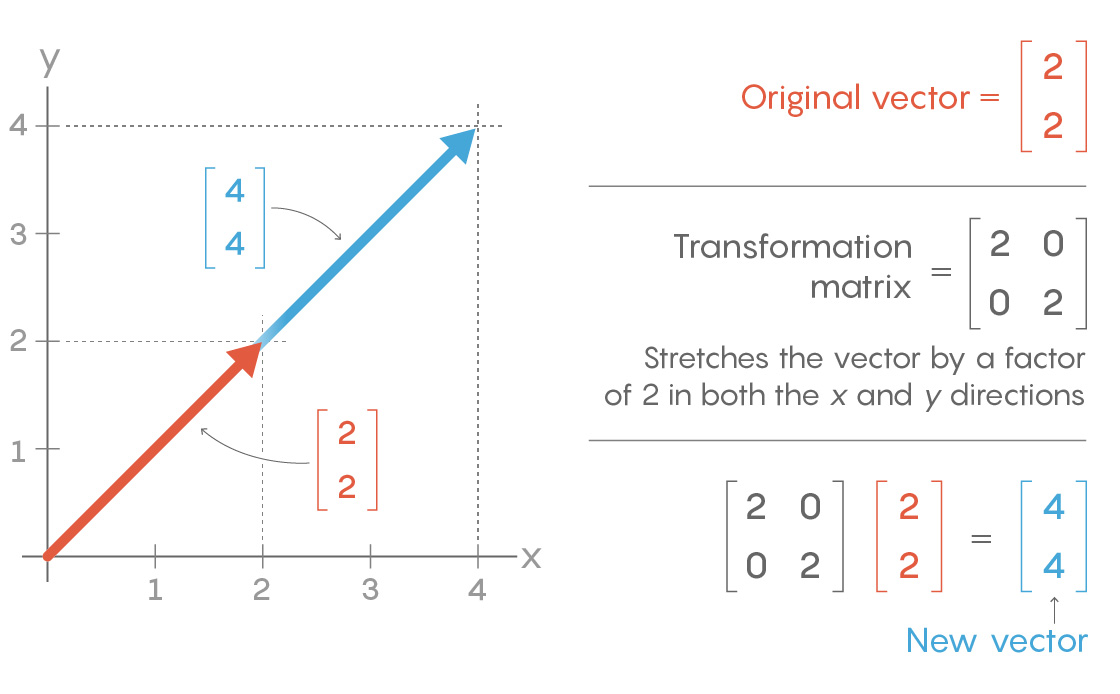
Other matrices perform different kinds of linear transformations, such as reflections, rotations and shears. There is also an “identity” matrix that leaves a vector unchanged (just as the identity symmetry leaves the triangle unchanged and the number 1 leaves other real numbers unchanged):

$latex \left[\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right]$

Linear algebra specifies the arithmetic behind those transformations. Matrices can be multiplied, added and subtracted as easily as we perform those operations on regular numbers.

Representation theory creates a bridge between group theory and linear algebra by assigning a matrix to each element in a group, according to certain rules. For example, the identity element in the group must be assigned the identity matrix. The assignments must also respect the relationships between the elements in the group. If a reflection multiplied by a given rotation equals a second reflection, then the matrix assigned to the first reflection multiplied by the matrix assigned to the rotation must equal the matrix assigned to the second reflection. A collection of matrices that respect these requirements is called a representation of a group.

A representation provides a simplified picture of a group, just as a grayscale photo can serve as a low-cost imitation of the original color image. Put another way, it “remembers” some basic but essential information about the group while forgetting the rest. Mathematicians aim to avoid grappling with the full complexity of a group; instead they gain a sense of its properties by looking at how it behaves when converted into the stripped-down format of linear transformations.

“We don’t have to look at the group at once,” Norton said. “We can look at a representation that’s smaller and still understand something about our group.”

A group can almost always be represented in multiple ways. S 3 , for example, has three distinct representations when real numbers are used to fill in the matrices: the trivial representation, the reflection representation and the sign representation.

Mathematicians collate the representations of a given group into a table — called a character table — that summarizes information about the group. The rows refer to each of the different representations, and the columns refer to important matrices within that representation: the matrix assigned to the identity element in the group, and the matrices assigned to the “generating” elements in the group that, together, give rise to all other elements. The entries of the table are a value called the “trace” of each matrix, calculated by summing the diagonal entries from the upper left of the matrix to the lower right. Below is the character table for the three representations of S 3 .

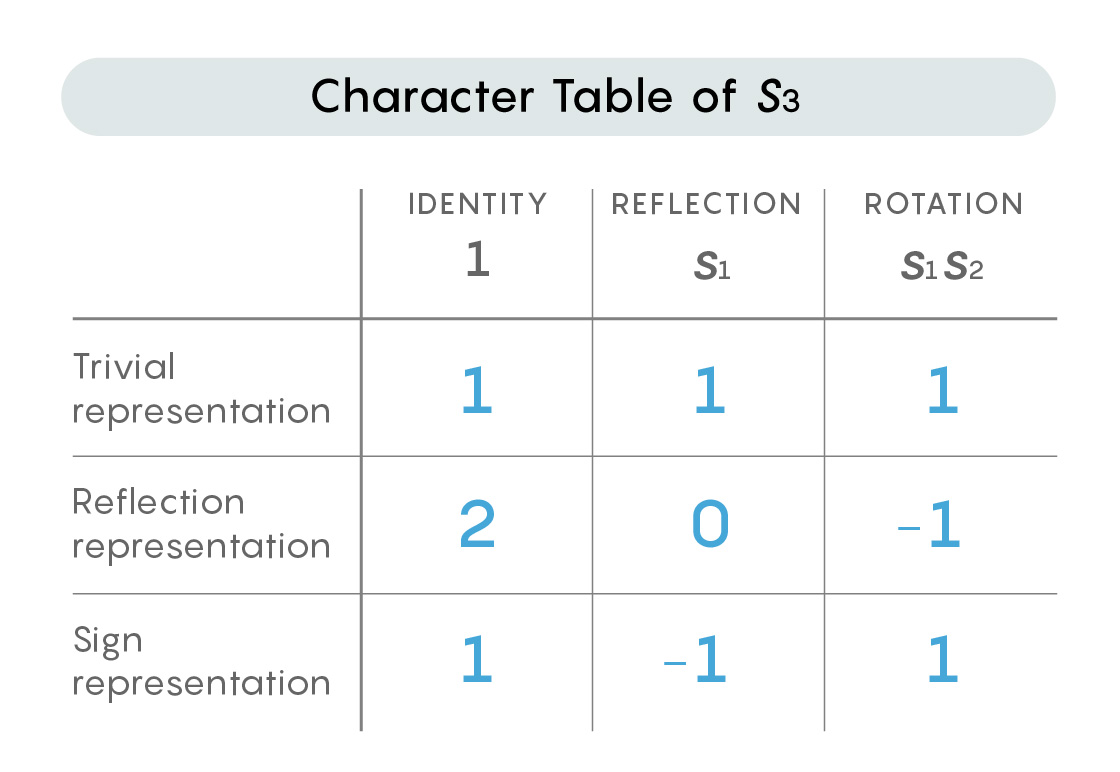
The character table provides a simplified picture of the group. Each representation within it provides slightly different information. Mathematicians combine the various perspectives provided by the representations into an overall impression of the group.

“You have a lot of different representations, which remember different things, and when you put all that information together you have this kaleidoscopic picture of your group in some sense,” Norton said.

The character table above is instantly recognizable to mathematicians as the one for S 3 . But sometimes the same character table can represent multiple groups — a degree of ambiguity that’s inevitable when you’re dealing with simplifications.

In those ambiguous cases, mathematicians have additional tools at their disposal. One is to change the number system in which they create the representation. The representation of S 3 above involves matrices with real-number entries, but you could also use complex number entries (where each number has a real part and an imaginary part). In fact, most of representation theory does.

Some of the most fruitful representations involve neither real numbers nor complex numbers. Instead, they use matrices with entries taken from miniature, or “modular,” number systems. This is the world of clock arithmetic , in which 7 + 6 wraps around the 12-hour clock to equal 1. Two groups that have the same character table with real-number representations might have different character tables with modular representations, allowing you to tell them apart.

Today, representation theory is a central tool in many mathematical fields: algebra, topology, geometry, mathematical physics and number theory — including the sweeping Langlands program .

“This philosophy of representation theory has gone on to gobble vast tracts of mathematics in the second half of the 20th century,” Williamson told me in an interview.

Representation theory — and modular representations in particular — played an important role in Andrew Wiles’ landmark 1994 proof of Fermat’s Last Theorem. The problem was about whether whole-number solutions exist for equations of the form a n + b n = c n . Wiles proved that no such solutions exist when n is greater than 2. Roughly, he argued that solutions, if they existed, would lead to a group (or “elliptic curve”) with very unusual properties. These properties were so unusual that it seemed possible to show that this object could not exist. However, directly proving its nonexistence was too difficult. Instead, Wiles worked with a family of modular representations that would have been attached to the group if it existed. He proved that this family of modular representations cannot exist, which meant that the group (or elliptic curve) cannot exist, which means that the solutions do not exist either.

Which in turn means that about 100 years after William Burnside dismissed representation theory as useless, it was a critical component in arguably the most celebrated proof of the 20th century.

“I couldn’t conceive of a proof of Fermat’s Last Theorem that doesn’t involve representation theory somewhere,” Weinstein said.

Correction : June 10, 2020 A previous version of this article didn’t specify that the real numbers only form a group under multiplication when you exclude zero. The article has been revised accordingly.

Get highlights of the most important news delivered to your email inbox

Also in Abstractions blog

Scientists Find a Fast Way to Describe Quantum Systems

Mathematicians Marvel at ‘Crazy’ Cuts Through Four Dimensions

Insects and Other Animals Have Consciousness, Experts Declare

Comment on this article.

Quanta Magazine moderates comments to facilitate an informed, substantive, civil conversation. Abusive, profane, self-promotional, misleading, incoherent or off-topic comments will be rejected. Moderators are staffed during regular business hours (New York time) and can only accept comments written in English. 

Next article

Use your social network.

Forgot your password ?

We’ll email you instructions to reset your password

Enter your new password

Representation Theory

Representation theory is fundamental in the study of objects with symmetry. 

It arises in contexts as diverse as card shuffling and quantum mechanics. An early success was the work of Schur and Weyl, who computed the representation theory of the symmetric and unitary groups; the answer is closely related to the classical theory of symmetric functions and deeper study leads to intricate questions in combinatorics.

More recently, methods from geometry and topology have greatly enhanced our understanding of these questions (“geometric representation theory”). The study of affine Lie algebras and quantum groups has brought many new ideas and viewpoints, and representation theory now furnishes a basic language for other fields, including the modern theory of automorphic forms.

All of these aspects are studied by Stanford faculty.  Topics of recent seminars include combinatorial representation theory as well as quantum groups.

Daniel Bump

Persi Diaconis

Publications Home — Over 100 years of publishing excellence

• Book Author Resources
• Submit a Book Proposal
• AMS Rights, Licensing, Permissions
• Open Math Notes
• Frequently Asked Questions
• Member Journals
• Research Journals
• Translation Journals
• Distributed Journals
• Open Access Journals
• Guidelines and Policies
• Journal Author Resources

Librarian Resources

• eBook Collections
• COUNTER Usage Statistics
• My Subscriptions
• Subscription Information
• Licensing Information

Mathematical Reviews/MathSciNet®

• MathSciNet ®
• Reviewer Home
• MathSciNet ® Subscriptions

Membership Home — Welcome to your membership center

Membership choices.

• Join the Society
• Renew your Membership
• Gift a Membership

Individual Membership

• Member Benefits
• Member Directory
• Reciprocating Societies
• Members in Developing Countries

Institutional Membership

• Domestic Institutions
• International Institutions
• Two-Year Institutions
• Graduate Student Chapter Program

Other Member Types

• Corporate Memberships
• Associate Memberships

Meetings & Conferences Home — Engage with colleagues and the latest research

National meetings.

• Joint Mathematics Meetings
• Upcoming JMMs
• Previous JMMs
• Special Lectures
• Professional Enhancement Programs (PEPs)

Sectional Meetings

• Upcoming Sectionals
• Previous Sectionals
• Presenting Papers
• Hosting Sectionals

Other Meetings, Conferences & Workshops

• Mathematics Research Communities
• Education Mini-conference
• International Meetings
• Mathematics Calendar
• Short Courses
• Workshop for Department Chairs and Leaders

Meetings Resources

• Suggest a Speaker
• AMS Meetings Grants
• Submitting Abstracts
• Welcoming Environment Policy
• MathSafe – supporting safe meetings

News & Outreach Home — Explore news, images, posters, and mathematical essays

News from the ams.

• AMS News Releases
• Feature Stories
• Information for Journalists
• In Memory Of

Math Voices

• Feature Column
• Math in the Media
• Column on Teaching and Learning

Explorations

• Recognizing Diverse Mathematicians
• AMS Posters
• Mathematics & Music
• Mathematical Imagery
• Mathematical Moments

Professional Programs Home — Resources and opportunities to further your mathematical pursuits

Professional development.

• Employment Services
• Mathjobs.org
• BEGIN Career Initiative
• Mathprograms.org
• Mathematical Opportunities Database
• Research Seminars

Institutional Information and Data

• Annual Survey of the Mathematical and Statistical Sciences
• CBMS Survey
• Other Sources of Data
• Directory of Institutions in the Mathematical Sciences
• Professional Directory

Grants & Support

• AMS-Simons Grants for PUI Faculty
• Travel Grants
• Fellowships & Scholarships
• Epsilon Fund
• Child Care Grants

Awards & Recognition

• AMS Prizes & Awards
• Fellows of the AMS

Education Home — Resources to support advanced mathematics teaching and learning

For students.

• Information for Undergraduate and High School Students
• Research Experiences for Undergraduates (REUs)
• Considering Grad School
• Find Grad Programs
• Applying to Grad School
• What do Mathematicians Do?

For Teachers

• Teaching Online
• Teaching Resources
• Inclusive Classrooms
• Assessing Student Learning
• Education Webinars

For Department Leaders & Mentors

• Information for Department Leaders
• paraDIGMS (Diversity in Graduate Mathematical Sciences)

Government Relations Home — Advocating for the mathematical sciences

Elevating mathematics in congress.

• Our Mission
• Letters, Statements, & Legislation
• Congressional Briefings

Legislative Priorities

• Federal Issues of Concern
• Federal Budget Process

Get Involved

• Advocacy Resources
• Take Action

DC-Based Fellowships

• Congressional Fellowship
• Mass Media Fellowship
• Catalyzing Advocacy in Science & Engineering (CASE) Fellowship

Giving to the AMS — Your gifts make great things happen for mathematics   Make a Gift

What you can support.

• The 2020 Fund
• Next Generation Fund
• Birman Fellowship for Women Scholars
• JMM Child Care Grants
• MathSciNet for Developing Countries

Create a Legacy

• Make a Tribute Gift
• Create a Permanent Fund
• Establish a Prize, Award or Fellowship
• Bequests and Charitable Estate Planning

Honoring Your Gift

• Donor Stories
• Donor Wall of Honor
• Thomas S. Fiske Society
• AMS Contributors Society
• AMS Gardens

Giving Resources

• AMS Development Committee
• AMS Gift Acceptance Policy

About the AMS — Advancing research. Connecting the mathematics community.

Our organization.

• Executive Staff
• Equity, Diversity, & Inclusion
• Jobs at AMS
• Customer Service

Our Governance

• Board of Trustees
• Executive Committee

Governance Operations

• Calendar of Meetings
• Policy Statements & Guidelines

On March 21 st , the AMS website will be down for regularly scheduled maintenance from 5:00am–8:00am

Introduction to Mathematical Modelling

What is a Mathematical Model? #

A mathematical model is a mathematical representation of a system used to make predictions and provide insight about a real-world scenario, and mathematical modelling is the process of constructing, simulating and evaluating mathematical models.

Why do we construct mathematical models? It can often be costly (or impossible!) to conduct experiments to study a real-world problem and so a mathematical model is a way to describe the behaviour of a system and predict outcomes using mathematical equations and computer simulations .

Check out the following resources to get started with mathematical modelling:

Chapter 1: What is Mathematical Modelling? in Principles of Mathematical Modeling

What is Math Modeling?

Wikipedia: Mathematical Model

Outline of the Modelling Process #

Mathematical modelling involves observing some real-world phenomenon and formulating a mathematical representation of the system. But how do we even know where to start? Or how to find a solution? The modelling process is a systematic approach:

Clearly state the problem

Identify variables and parameters

Make assumptions and identify constraints

Build solutions

Analyze and assess

Report the results

Models can have a wide range of complexity ! More complex does not necessarily mean better and we can sometimes work with more simplistic models to achieve good results. In many instances, we often start with a simple model and then build-up the complexity by iterating through the steps in modelling process until the model accurately describes the real-world application.

Check out Math Modeling: Getting Started and Getting Solutions to read more about the modelling process.

Types of Models #

There are many different types of mathematical models! In this course we focus on the following:

Deterministic models predict future based on current information and do not include randomness. These kinds of models often take the from of systems of differential equations which describe the evolution of a system over time.

Stochastic models include randomness and are based on probability distributions and stochastic processes .

Data-driven models look for patterns in observed data to predict the output of a system. These kinds of models often take the form of functions with parameters computed to fit observed data.