- Maths Questions

Pythagoras Theorem Questions

Pythagoras theorem questions with detailed solutions are given for students to practice and understand the concept. Practising these questions will be a plus point in preparation for examinations. Let us discuss in brief about the Pythagoras theorem.
Pythagoras’ theorem is all about the relation between sides of a right-angled triangle. According to the theorem, the hypotenuse square equals the sum of squares of the perpendicular sides.
Click here to learn the proof of Pythagoras’ Theorem .
Video Lesson on Pythagoras Theorem
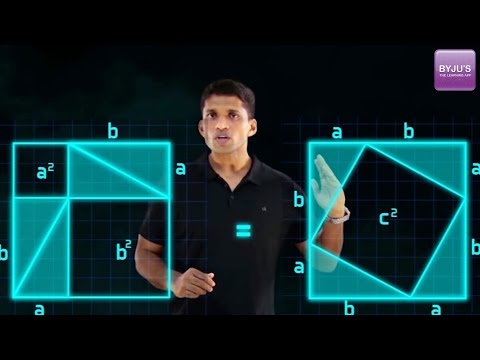
Pythagoras Theorem Questions with Solutions
Now that we have learnt about the Pythagoras Theorem, lets apply the same by solving the following questions.
Question 1: In a right-angled triangle, the measures of the perpendicular sides are 6 cm and 11 cm. Find the length of the third side.
Let ΔABC be the triangle, right-angled at B, such that AB and BC are the perpendicular sides. Let AB = 6 cm and BC = 11 cm
Then, by the Pythagoras theorem,
AC 2 = AB 2 + BC 2
\(\begin{array}{l}\Rightarrow AC=\sqrt{(AB^{2}+BC^{2})}=\sqrt{6^{2}+11^{2}}\end{array} \)
\(\begin{array}{l}=\sqrt{36+121}=\sqrt{157}\end{array} \)
∴ AC = √157 cm.
Question 2: A triangle is given whose sides are of length 21 cm, 20 cm and 29 cm. Check whether these are the sides of a right-angled triangle.
If these are the sides of a right-angled triangle, it must satisfy the Pythagoras theorem.
We have to check whether 21 2 + 20 2 = 29 2
Now, 21 2 + 20 2 = 441 + 400 = 841 = 29 2
Thus, the given triangle is a right-angled triangle.
Question 3: Find the Pythagorean triplet with whose one number is 6.
Now, m 2 + 1 = 9 + 1 = 10
and m 2 – 1 = 9 – 1 = 8
Therefore, the Pythagorean triplet is (6, 8, 10).
Question 4: The length of the diagonal of a square is 6 cm. Find the sides of the square.
Let ABCD be the square, and let AC be the diagonal of length 6 cm. Then triangle ABC is the right-angled triangle such that AB = BC (∵ all sides of a square are equal)
By Pythagoras theorem,
⇒ AC 2 = 2AB 2
⇒ AC = √2 AB
⇒ AB = (1/√2) AC = (1/√2)6 = 3√2 cm.
Question 5: A ladder is kept at a distance of 15 cm from the wall such that the top of the ladder is at the height of 8 cm from the bottom of the wall. Find the length of the wall.
Let AB be the ladder of length x.

AC 2 + BC 2 = AB 2
\(\begin{array}{l}\Rightarrow AB=\sqrt{AC^{2}+BC^{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow x=\sqrt{8^{2}+15^{2}}=\sqrt{64+225}\end{array} \)
⇒ x = 17 cm
∴ Length of the ladder is 17 cm.
Question 6: Find the area of a rectangle whose length is 144 cm and the length of the diagonal 145 cm.
Let the rectangle be ABCD

\(\begin{array}{l}\Rightarrow AD=\sqrt{AC^{2}-CD^{2}}=\sqrt{145^{2}-144^{2)}\end{array} \)
⇒ AD = √(21025 – 20736) = √289
⇒ AD = 17 cm
Thus, area of the rectangle ABCD = 17 × 144 = 2448 cm 2 .
- Properties of Triangles
- Congruence of Triangles
- Similar Triangles
- Trigonometry
Question 7: A boy travels 24 km towards east from his house, then he turned his left and covers another 10 km. Find out his total displacement?
Let the boy’s house is at point O, then to find the total displacement, we have to find OB.

Clearly, ΔOAB is a right-angled triangle, by Pythagoras theorem,
\(\begin{array}{l} OB=\sqrt{OA^{2}+AB^{2}}=\sqrt{24^{2}-10^{2}}\end{array} \)
⇒ OB = √(576 + 100) = √676
⇒ OB = 26 km.
Question 8: Find the distance between a tower and a building of height 65 m and 34 m, respectively, such that the distance between their top is 29 m.
The figure below shows the situation. Let x be the distance between the tower and the building.

In right triangle DCE, by Pythagoras theorem,
CE = √(DE 2 – DC 2 ) = √(29 2 – 21 2 )
⇒ x = √(841 – 441) = √400
⇒ x = 20 m.
∴ the distance between the tower and the building is 20 m.
Question 9: Find the area of the triangle formed by the chord of length 10 cm of the circle whose radius is 13 cm.
Let AB be the chord of the circle with the centre at O such that AB = 10 and OA = OB = 13. Draw a perpendicular OM on AB.

By the property of circle, perpendicular dropped from the centre of the circle on a chord, bisects the chord.
Then, AM = MB = 5 cm.
Now, in right triangle OMB,
OB 2 = OM 2 + MB 2
⇒ OM = √(OB 2 – MB 2 )
⇒ OM = √(13 2 – 5 2 ) = √(169 – 25)
⇒ OM = √144 = 12 cm
Area of triangle OAB = ½ × AB × OM
= ½ × 10 × 12
= 60 cm 2 .
Question 10: Find the length of tangent PT where P is a point which is at a distance 10 cm from the centre O of the circle of radius 6 cm.
Given, OP = 10 cm and OT = 6m.
We have to find the value of PT.

By the property of tangents, the radius of the circle is perpendicular to the tangent at the point of contact.
Thus, triangle OTP is a right-angled triangle.
∴ by the Pythagoras theorem,
OP 2 = OT 2. + PT 2
⇒ PT = √(OP 2 – OT 2 ) = √(10 2 – 6 2 )
⇒ PT = √(100 – 36) = √64
⇒ PT = 8 cm.

Related Video on Pythagorean Triples

Practice Questions on Pythagoras Theorem
1. Find the area of a right-angled triangle whose hypotenuse is 13 cm and one of the perpendicular sides is 5 cm.
2. Find the Pythagorean triplet whose one member is 15.
3. Find the perimeter of a rectangle whose diagonal is 5 cm and one of its sides is 4 cm.
4 if a pole of length 65 cm is kept leaning against a wall such that the pole reaches up to a height of 63 cm on the wall from the ground. Find the distance between the pole and the wall.
5. Find the area of the triangle inscribed within a circle of radius 8.5 cm such that one of the sides of the triangle is the diameter of the circle and the length of the other side is 8 cm.
(Hint: The triangle is formed in semi-circular region and angle of a semi-circle is of 90 o )
Learn about various mathematical concepts in a simple manner with detailed information, along with step by step solutions to all questions, only at BYJU’S. Download BYJU’S – The Learning App to get personalised videos.
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
